7.5正态分布 课件(共24张PPT)-2023-2024学年高二下学期数学人教A版(2019)选择性必修第三册
文档属性
| 名称 | 7.5正态分布 课件(共24张PPT)-2023-2024学年高二下学期数学人教A版(2019)选择性必修第三册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-21 00:00:00 | ||
图片预览




文档简介
(共24张PPT)
7.5 正态分布
复习回顾
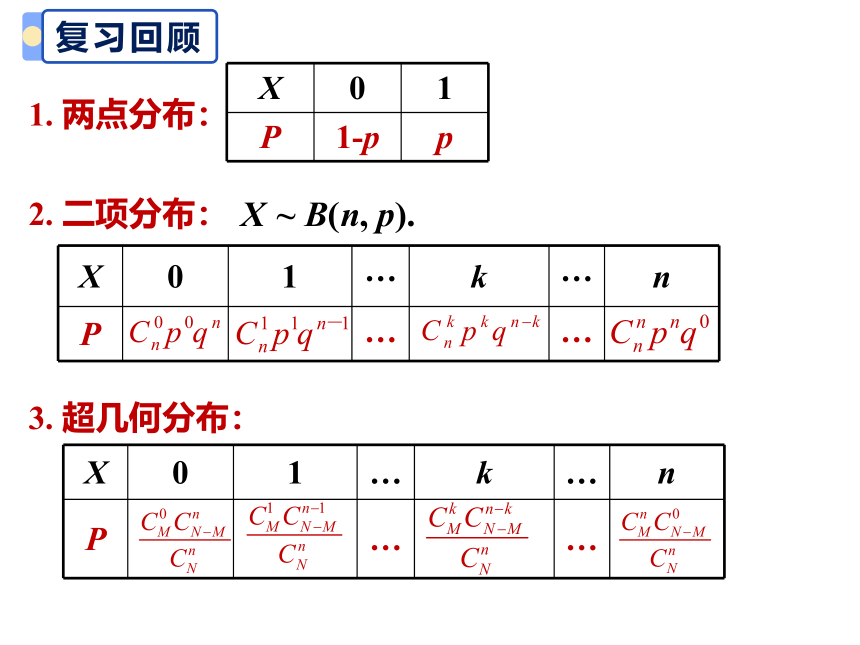
1. 两点分布:
X 0 1
P 1-p p
2. 二项分布:
X 0 1 … k … n
P … …
3. 超几何分布:
X 0 1 … k … n
P … …
情境引入
现实中,除了前面已经研究过的离散型随机变量外,还有大量问题中的随机变量不是离散型的,它们的取值往往充满某个区间甚至整个实轴,但取一点的概率为0,我们称这类随机变量为连续型随机变量.
问题探究
25.39 25.36 25.34 25.42 25.45 25.38 25.39 25.42
25.47 25.35 25.41 25.43 25.44 25.48 25.45 25.43
25.46 25.40 25.51 25.45 25.40 25.39 25.41 25.36
25.38 25.31 25.56 25.43 25.40 25.38 25.37 25.44
25.33 25.46 25.40 25.49 25.34 25.42 25.50 25.37
25.35 25.32 25.45 25.40 25.27 25.43 25.54 25.39
25.45 25.43 25.40 25.43 25.44 25.41 25.53 25.37
25.38 25.24 25.44 25.40 25.36 25.42 25.39 25.46
25.38 25.35 25.31 25.34 25.40 25.36 25.41 25.32
25.38 25.42 25.40 25.33 25.37 25.41 25.49 25.35
25.47 25.34 25.30 25.39 25.36 25.46 25.29 25.40
25.37 25.33 25.40 25.35 25.41 25.37 25.47 25.39
25.42 25.47 25.38 25.39
1.某钢铁加工厂生产内径为25.40mm的钢管,为了检验产品的质量,从一批产品中任取100件检测,用X表示它们的实际尺寸,测得X的值如下:
如何描述这100个样本数据的分布
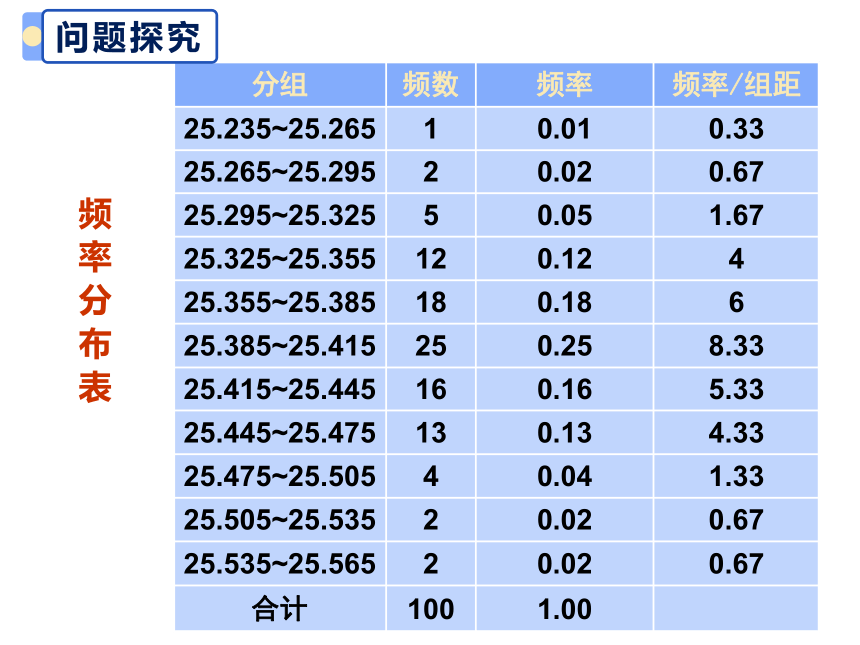
分组 频数 频率 频率/组距
25.235~25.265 1 0.01 0.33
25.265~25.295 2 0.02 0.67
25.295~25.325 5 0.05 1.67
25.325~25.355 12 0.12 4
25.355~25.385 18 0.18 6
25.385~25.415 25 0.25 8.33
25.415~25.445 16 0.16 5.33
25.445~25.475 13 0.13 4.33
25.475~25.505 4 0.04 1.33
25.505~25.535 2 0.02 0.67
25.535~25.565 2 0.02 0.67
合计 100 1.00
频 率 分 布 表
问题探究
问题探究
产品
尺寸
(mm)
频率
组距
25.235
25.295
25.355
25.415
25.475
25.535
25.265
25.325
25.385
25.445
25.505
25.565
2
4
6
8
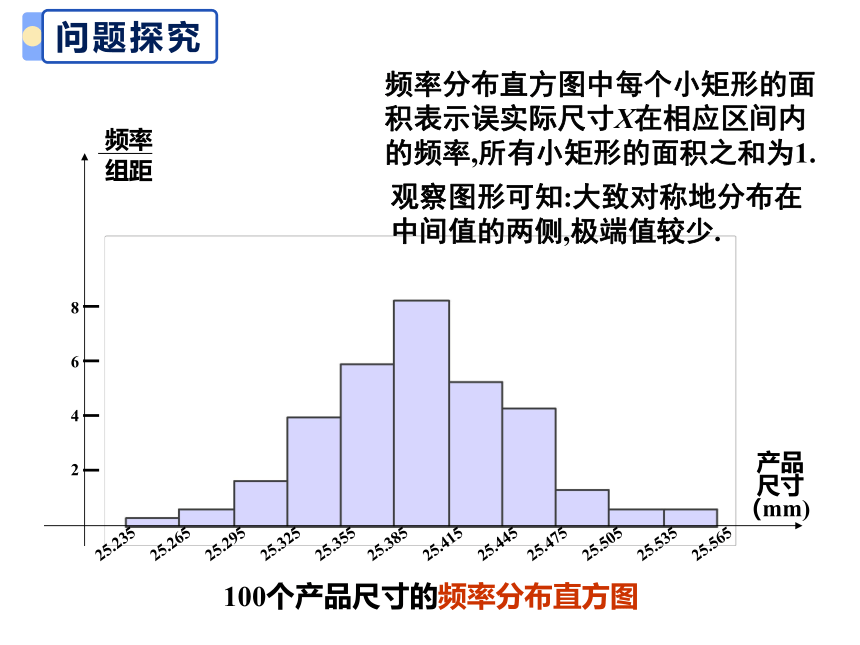
100个产品尺寸的频率分布直方图
频率分布直方图中每个小矩形的面积表示误实际尺寸X在相应区间内的频率,所有小矩形的面积之和为1.
观察图形可知:大致对称地分布在中间值的两侧,极端值较少.
问题探究
200个产品尺寸的频率分布直方图
频率
组距
产品
尺寸
(mm)
问题探究
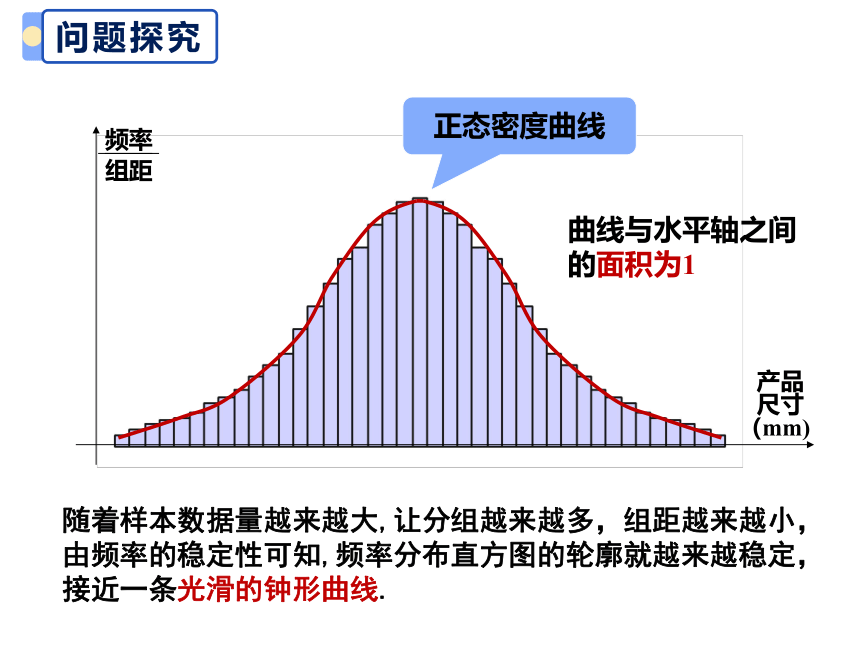
正态密度曲线
产品
尺寸
(mm)
频率
组距
随着样本数据量越来越大,让分组越来越多,组距越来越小,由频率的稳定性可知,频率分布直方图的轮廓就越来越稳定,接近一条光滑的钟形曲线.
曲线与水平轴之间的面积为1
知识要点
x
y
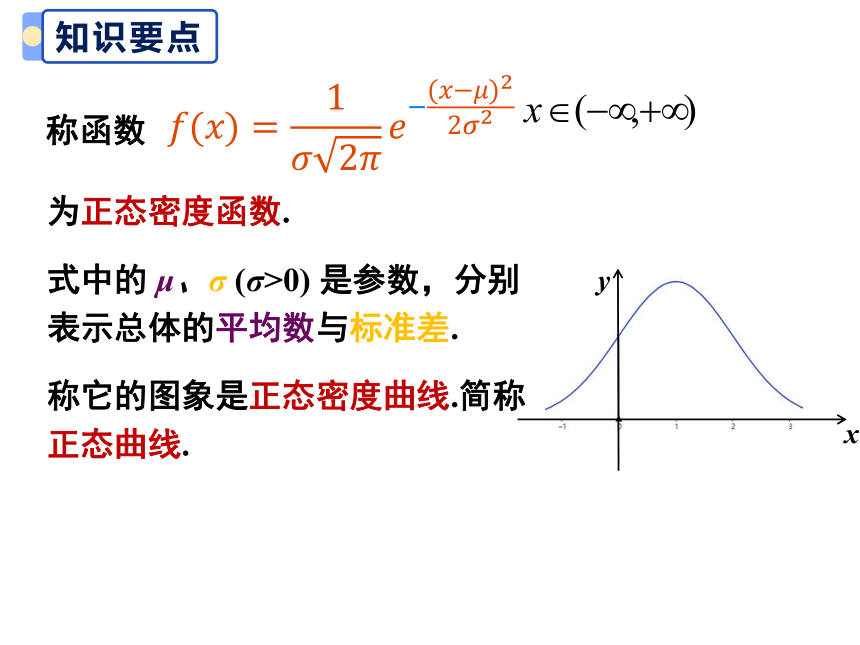
称函数
为正态密度函数.
式中的 μ、σ (σ>0) 是参数,分别表示总体的平均数与标准差.
称它的图象是正态密度曲线.简称正态曲线.
知识要点
若随机变量X的概率分布密度函数为
则称随机变量X 服从正态分布,记为X~N(μ,2).
知识要点
正态曲线的性质 :
且对称区域面积相等;
具有两头低、中间高、左右对称的基本特征.
(5)当 无限增大时,曲线无限接近x轴.
知识要点
正态曲线的性质 :
σ越大,表示总体的分布越分散;
σ越小,表示总体的分布越集中.
μ=-1
μ=0
μ=1
σ=1
μ=0
=0.5
=1
=2
知识要点
正态函数表示式:
当 μ= 0,σ=1时,可得
标准正态函数表示式:
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
标准正态 曲线
标准正态曲线:
知识要点
在实际遇到的许多随机现象都服从或近似服从正态分布:
在生产中,各种产品的质量指标;
在测量中,各种测量结果;
在生物学中,同一群体的某一特征如身高、体重等……;
在气象中,某地每年七月份的平均气温、平均湿度、
以及降雨量、水位等;
总之,正态分布广泛存在于自然界、生产及科学技术的许多领域中. 正态分布在概率和统计中占有重要地位.
小试牛刀
【答案】A
1. 设两个正态分布N(μ1,σ12)和N(μ2,σ22)(σ2>0)的密度函数图像如图,则有( )
A. μ1< μ2 , σ1<σ2 B. μ1< μ2 , σ1>σ2
A. μ1> μ2 , σ1<σ2 B. μ1>μ2 , σ1>σ2
小试牛刀
【答案】C
2.
正态曲线在特殊区间上的概率:
知识要点
正态总体在 以外取值的概率只有 0.27 % , 通常
认为这种情况在一次试验中几乎不可能发生,称为小概率事件.
在实际应用中,通常认为服从于正态分布 x~N(μ,2) 的随机变量X只取 中的值,这在统计学中称为3原则.
学以致用
例1 在某次考试中,考生的成绩X服从正态分布,即 X~N(90,100)
(1)求考试成绩X位于区间(70,110]上的概率是多少?
(2)若这次考试共有2000名考生,试估计考试成绩在(80,100]
之间的考生大约有多少人?
[解] ∵X~N(90,100),∴μ=90,σ=10.
(1)在该正态分布中,μ-2σ=70,μ+2σ=110,
∵P(μ-2σ∴考试成绩X位于区间(70,110]内的概率为0.9545.
学以致用
例1 在某次考试中,考生的成绩X服从正态分布,即 X~N(90,100)
(1)求考试成绩X位于区间(70,110]上的概率是多少?
(2)若这次考试共有2000名考生,试估计考试成绩在(80,100]
之间的考生大约有多少人?
(2)μ-σ=80,μ+σ=100,
∵P(μ-σ∴考试成绩X位于区间(80,100]内的概率为0.6827.
由共有2000名考生,知考试成绩在(80,100]间的考生大约有2000×0.6827≈1 365(人).
例2 若X~N(5,1),求P(6解: 因为X~N(5,1),
故正态密度曲线关于直线 x=5 对称,
小试牛刀
1).若X~N(μ,σ2),问X位于区域(μ,μ+σ)内的概率是多少?
解:由正态曲线的对称性可得,
课堂小结
1. 正态曲线及正态密度函数
2. 正态分布
3. 正态曲线的性质
(1)对称性:曲线是单峰的,它关于直线x=μ对称.
(2)最值性:曲线在x=μ处达到峰值(最高点)
(3)当|x|无限增大时,曲线无限接近x轴.
课堂小结
4. 正态分布的3σ原则
7.5 正态分布
复习回顾
1. 两点分布:
X 0 1
P 1-p p
2. 二项分布:
X 0 1 … k … n
P … …
3. 超几何分布:
X 0 1 … k … n
P … …
情境引入
现实中,除了前面已经研究过的离散型随机变量外,还有大量问题中的随机变量不是离散型的,它们的取值往往充满某个区间甚至整个实轴,但取一点的概率为0,我们称这类随机变量为连续型随机变量.
问题探究
25.39 25.36 25.34 25.42 25.45 25.38 25.39 25.42
25.47 25.35 25.41 25.43 25.44 25.48 25.45 25.43
25.46 25.40 25.51 25.45 25.40 25.39 25.41 25.36
25.38 25.31 25.56 25.43 25.40 25.38 25.37 25.44
25.33 25.46 25.40 25.49 25.34 25.42 25.50 25.37
25.35 25.32 25.45 25.40 25.27 25.43 25.54 25.39
25.45 25.43 25.40 25.43 25.44 25.41 25.53 25.37
25.38 25.24 25.44 25.40 25.36 25.42 25.39 25.46
25.38 25.35 25.31 25.34 25.40 25.36 25.41 25.32
25.38 25.42 25.40 25.33 25.37 25.41 25.49 25.35
25.47 25.34 25.30 25.39 25.36 25.46 25.29 25.40
25.37 25.33 25.40 25.35 25.41 25.37 25.47 25.39
25.42 25.47 25.38 25.39
1.某钢铁加工厂生产内径为25.40mm的钢管,为了检验产品的质量,从一批产品中任取100件检测,用X表示它们的实际尺寸,测得X的值如下:
如何描述这100个样本数据的分布
分组 频数 频率 频率/组距
25.235~25.265 1 0.01 0.33
25.265~25.295 2 0.02 0.67
25.295~25.325 5 0.05 1.67
25.325~25.355 12 0.12 4
25.355~25.385 18 0.18 6
25.385~25.415 25 0.25 8.33
25.415~25.445 16 0.16 5.33
25.445~25.475 13 0.13 4.33
25.475~25.505 4 0.04 1.33
25.505~25.535 2 0.02 0.67
25.535~25.565 2 0.02 0.67
合计 100 1.00
频 率 分 布 表
问题探究
问题探究
产品
尺寸
(mm)
频率
组距
25.235
25.295
25.355
25.415
25.475
25.535
25.265
25.325
25.385
25.445
25.505
25.565
2
4
6
8
100个产品尺寸的频率分布直方图
频率分布直方图中每个小矩形的面积表示误实际尺寸X在相应区间内的频率,所有小矩形的面积之和为1.
观察图形可知:大致对称地分布在中间值的两侧,极端值较少.
问题探究
200个产品尺寸的频率分布直方图
频率
组距
产品
尺寸
(mm)
问题探究
正态密度曲线
产品
尺寸
(mm)
频率
组距
随着样本数据量越来越大,让分组越来越多,组距越来越小,由频率的稳定性可知,频率分布直方图的轮廓就越来越稳定,接近一条光滑的钟形曲线.
曲线与水平轴之间的面积为1
知识要点
x
y
称函数
为正态密度函数.
式中的 μ、σ (σ>0) 是参数,分别表示总体的平均数与标准差.
称它的图象是正态密度曲线.简称正态曲线.
知识要点
若随机变量X的概率分布密度函数为
则称随机变量X 服从正态分布,记为X~N(μ,2).
知识要点
正态曲线的性质 :
且对称区域面积相等;
具有两头低、中间高、左右对称的基本特征.
(5)当 无限增大时,曲线无限接近x轴.
知识要点
正态曲线的性质 :
σ越大,表示总体的分布越分散;
σ越小,表示总体的分布越集中.
μ=-1
μ=0
μ=1
σ=1
μ=0
=0.5
=1
=2
知识要点
正态函数表示式:
当 μ= 0,σ=1时,可得
标准正态函数表示式:
0
1
2
-1
-2
x
y
-3
3
μ=0
σ=1
标准正态 曲线
标准正态曲线:
知识要点
在实际遇到的许多随机现象都服从或近似服从正态分布:
在生产中,各种产品的质量指标;
在测量中,各种测量结果;
在生物学中,同一群体的某一特征如身高、体重等……;
在气象中,某地每年七月份的平均气温、平均湿度、
以及降雨量、水位等;
总之,正态分布广泛存在于自然界、生产及科学技术的许多领域中. 正态分布在概率和统计中占有重要地位.
小试牛刀
【答案】A
1. 设两个正态分布N(μ1,σ12)和N(μ2,σ22)(σ2>0)的密度函数图像如图,则有( )
A. μ1< μ2 , σ1<σ2 B. μ1< μ2 , σ1>σ2
A. μ1> μ2 , σ1<σ2 B. μ1>μ2 , σ1>σ2
小试牛刀
【答案】C
2.
正态曲线在特殊区间上的概率:
知识要点
正态总体在 以外取值的概率只有 0.27 % , 通常
认为这种情况在一次试验中几乎不可能发生,称为小概率事件.
在实际应用中,通常认为服从于正态分布 x~N(μ,2) 的随机变量X只取 中的值,这在统计学中称为3原则.
学以致用
例1 在某次考试中,考生的成绩X服从正态分布,即 X~N(90,100)
(1)求考试成绩X位于区间(70,110]上的概率是多少?
(2)若这次考试共有2000名考生,试估计考试成绩在(80,100]
之间的考生大约有多少人?
[解] ∵X~N(90,100),∴μ=90,σ=10.
(1)在该正态分布中,μ-2σ=70,μ+2σ=110,
∵P(μ-2σ
学以致用
例1 在某次考试中,考生的成绩X服从正态分布,即 X~N(90,100)
(1)求考试成绩X位于区间(70,110]上的概率是多少?
(2)若这次考试共有2000名考生,试估计考试成绩在(80,100]
之间的考生大约有多少人?
(2)μ-σ=80,μ+σ=100,
∵P(μ-σ
由共有2000名考生,知考试成绩在(80,100]间的考生大约有2000×0.6827≈1 365(人).
例2 若X~N(5,1),求P(6
故正态密度曲线关于直线 x=5 对称,
小试牛刀
1).若X~N(μ,σ2),问X位于区域(μ,μ+σ)内的概率是多少?
解:由正态曲线的对称性可得,
课堂小结
1. 正态曲线及正态密度函数
2. 正态分布
3. 正态曲线的性质
(1)对称性:曲线是单峰的,它关于直线x=μ对称.
(2)最值性:曲线在x=μ处达到峰值(最高点)
(3)当|x|无限增大时,曲线无限接近x轴.
课堂小结
4. 正态分布的3σ原则
