1.2.2相反数 课件(共19张PPT) 2024-2025学年数学沪科版(2024)七年级上册
文档属性
| 名称 | 1.2.2相反数 课件(共19张PPT) 2024-2025学年数学沪科版(2024)七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 597.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
1.2 数轴、相反数和绝对值
课时2 相反数
1.借助数轴理解相反数的概念,并能求一个有理数的相反数,知道互为相反数在数轴上的位置关系;
2.会利用相反数对含多重符号的数进行化简;
3.通过从数和形两个方面理解相反数,体会数形结合的思想方法;
4.通过由具体实例抽象概括的独立思考与合作学习的过程,培养学生积极参与、善于与他人合作交流的学习习惯.
学习目标
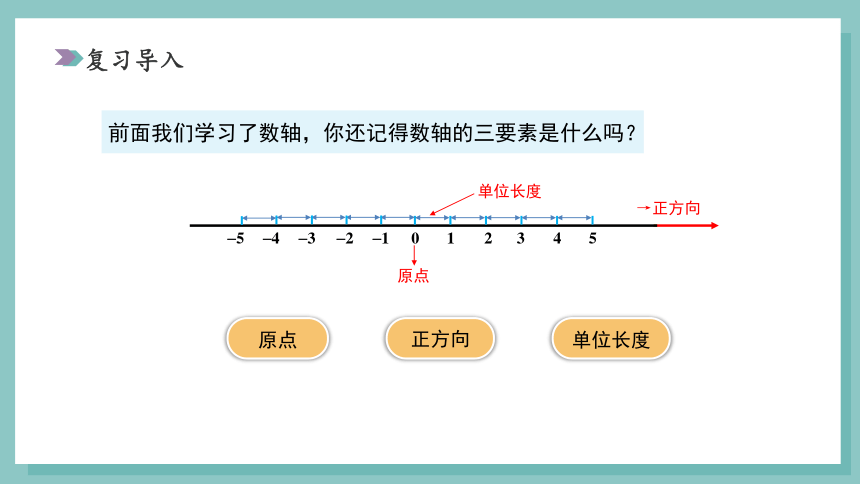
前面我们学习了数轴,你还记得数轴的三要素是什么吗?
原点
正方向
单位长度
0
单位长度
1
原点
2
3
4
5
1
2
3
4
5
→正方向
复习导入
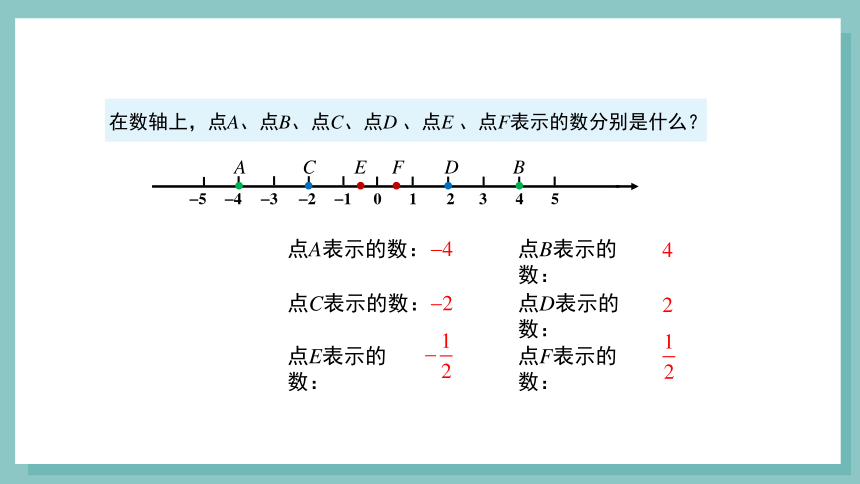
在数轴上,点A、点B、点C、点D 、点E 、点F表示的数分别是什么?
0
1
2
3
4
5
1
2
3
4
5
A
B
C
D
E
F
点A表示的数:
点B表示的数:
点C表示的数:
点D表示的数:
4
4
2
2
点E表示的数:
点F表示的数:
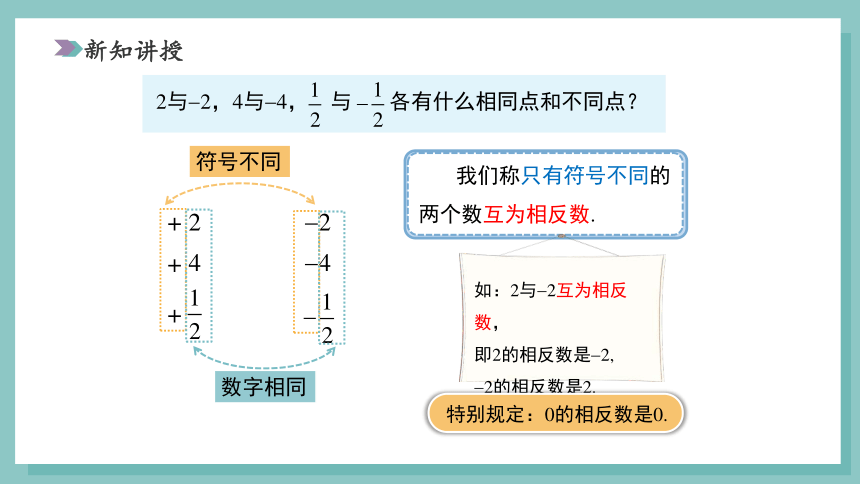
2与 2,4与 4, 与 各有什么相同点和不同点?
2
2
4
4
+
+
+
符号不同
数字相同
我们称只有符号不同的两个数互为相反数.
如:2与 2互为相反数,
即2的相反数是 2,
2的相反数是2.
特别规定:0的相反数是0.
新知讲授
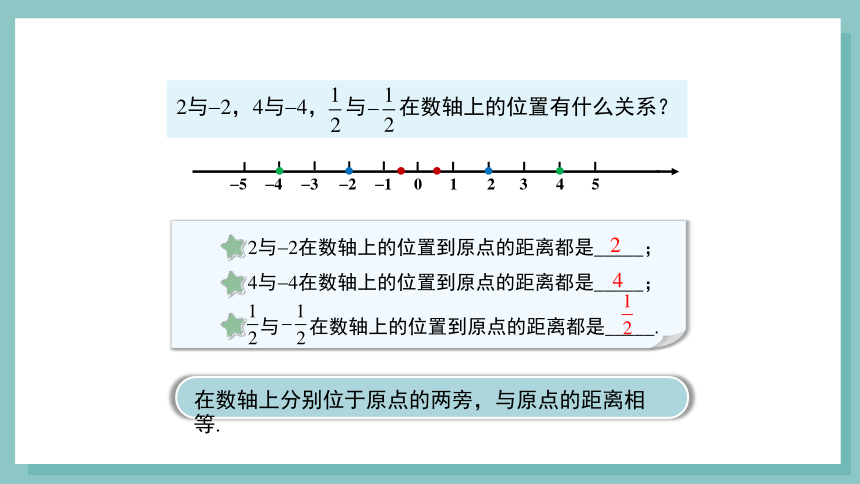
2与 2,4与 4, 与 在数轴上的位置有什么关系?
0
1
2
3
4
5
1
2
3
4
5
2与 2在数轴上的位置到原点的距离都是_____;
4与 4在数轴上的位置到原点的距离都是_____;
与 在数轴上的位置到原点的距离都是_____.
2
4
在数轴上分别位于原点的两旁,与原点的距离相等.
设a是一个正数,数轴上与原点的距离等于a的点有几个?这些点表示的数有什么关系?
0
1
2
3
1
2
3
4
4
5
5
6
6
a
a
a
a
两个
原点左右各一个
a与a互为相反数
两个互为相反数的数在数轴上所表示的点在原点的两旁,与原点的距离相等.
探究
(个数上)
(形式上)
(位置上)
两个互为相反数的数在数轴上表示的点在原点的两旁,与原点的距离相等.
互为相反数的数的特征
2个,成对出现
只有符号不同
(0特殊)
归纳总结
1.判断下列说法是否正确:
(1) 5是相反数;
(2)+3是相反数;
(3)3是 3的相反数;
(4) 3与+3互为相反数.
5是5的相反数
+3是 3的相反数
练一练
2.写出下列各数的相反数:
6, 8, ,3.9 ,100 , ,0 .
解:6的相反数是6;
3.9的相反数是3.9 ;
100的相反数是100;
8的相反数是8 ;
0的相反数是0.
的相反数是 ;
的相反数是 ;
观察下列语句,你能得出什么结论?
6的相反数是6;
3.9的相反数是3.9;
100的相反数是100.
8的相反数是8 ;
0的相反数是0.
的相反数是 ;
的相反数是 .
正数的相反数是负数;
负数的相反数是正数;
0的相反数是0.
所有的数
都有相反数
一般地,a的相反数记作 a.这里a表示任意一个数,它可以是正数、负数或者0.
求a的相反数就在a前面添“-”
观察思考
+8
( )
8
+100
100
8
= +8
3.9
= +3.9
试着化简下列式子:
= +
( )
( )
( )
( )
( )
双重符号化简,同号得正,异号得负.
+8的相反数
8的相反数
在任意一个数前面添上“ ”号,所得的数就是原数的相反数.
拓展
简化符号:
( 3) =____; (+0.73)=______;
0=______; ( 34)=_____;
+( 7)=_____.
3
0.73
0
34
7
(+a)= a
( a)= a
+(+a)= a
+( a)= a
“+”可省略
双重符号化简,
异号得负.
同号得正,
练一练
【例1】写出下列各数的相反数:
3, 7, 2.1, , ,0,20.
解:3的相反数是 3, 7的相反数是7, 2.1的相反数是2.1, 的相反数是 , 的相反数是 ,0
的相反数是0,20的相反数是 20.
典型例题
【例2】简化符号:
( 6) =_____;
(+6)=______;
+( 6) =_____;
+(+6)=______.
6
6
6
6
双重符号化简,
异号得负.
同号得正,
1.下列说法正确的是( )
A.带“+”和带“ ”的数互为相反数;
B.数轴上原点两侧的两个点表示的数是相反数;
C.a的相反数是负数;
D.相反数是本身的数只有0.
D
当堂检测
2.填空:
(1) 2.8是 的相反数, 的相反数是3.2;
(2) (+4)是 的相反数, ( 7) 是 的相反数;
(3) (+8)= , ( 9) = .
2.8
3.2
4
7
8
9
3.简化符号:
[+( 6)]=_____;
[ ( 6)]=_____;
{ [ (+6)]}=_____.
选做
在任意一个数前面添上“ ”号,所得的数就是原数的相反数.多重符号从里往外化简即可.
分析
6
6
6
多重符号化简:
“-”有奇数个,结果有“-”
“-”有偶数个,结果无“-”
课堂小结
相反数
一般地,设 a 是一个正数,数轴上与原点的距离是 a 的点有___个,它们分别在正、负半轴上,表示____和_____,这两个数只有______不同.
只有____不同的两个数,互为相反数.
a 的相反数是___;
0 的相反数是___.
符号
符号
0
a
-a
两
-a
-a a
1.2 数轴、相反数和绝对值
课时2 相反数
1.借助数轴理解相反数的概念,并能求一个有理数的相反数,知道互为相反数在数轴上的位置关系;
2.会利用相反数对含多重符号的数进行化简;
3.通过从数和形两个方面理解相反数,体会数形结合的思想方法;
4.通过由具体实例抽象概括的独立思考与合作学习的过程,培养学生积极参与、善于与他人合作交流的学习习惯.
学习目标
前面我们学习了数轴,你还记得数轴的三要素是什么吗?
原点
正方向
单位长度
0
单位长度
1
原点
2
3
4
5
1
2
3
4
5
→正方向
复习导入
在数轴上,点A、点B、点C、点D 、点E 、点F表示的数分别是什么?
0
1
2
3
4
5
1
2
3
4
5
A
B
C
D
E
F
点A表示的数:
点B表示的数:
点C表示的数:
点D表示的数:
4
4
2
2
点E表示的数:
点F表示的数:
2与 2,4与 4, 与 各有什么相同点和不同点?
2
2
4
4
+
+
+
符号不同
数字相同
我们称只有符号不同的两个数互为相反数.
如:2与 2互为相反数,
即2的相反数是 2,
2的相反数是2.
特别规定:0的相反数是0.
新知讲授
2与 2,4与 4, 与 在数轴上的位置有什么关系?
0
1
2
3
4
5
1
2
3
4
5
2与 2在数轴上的位置到原点的距离都是_____;
4与 4在数轴上的位置到原点的距离都是_____;
与 在数轴上的位置到原点的距离都是_____.
2
4
在数轴上分别位于原点的两旁,与原点的距离相等.
设a是一个正数,数轴上与原点的距离等于a的点有几个?这些点表示的数有什么关系?
0
1
2
3
1
2
3
4
4
5
5
6
6
a
a
a
a
两个
原点左右各一个
a与a互为相反数
两个互为相反数的数在数轴上所表示的点在原点的两旁,与原点的距离相等.
探究
(个数上)
(形式上)
(位置上)
两个互为相反数的数在数轴上表示的点在原点的两旁,与原点的距离相等.
互为相反数的数的特征
2个,成对出现
只有符号不同
(0特殊)
归纳总结
1.判断下列说法是否正确:
(1) 5是相反数;
(2)+3是相反数;
(3)3是 3的相反数;
(4) 3与+3互为相反数.
5是5的相反数
+3是 3的相反数
练一练
2.写出下列各数的相反数:
6, 8, ,3.9 ,100 , ,0 .
解:6的相反数是6;
3.9的相反数是3.9 ;
100的相反数是100;
8的相反数是8 ;
0的相反数是0.
的相反数是 ;
的相反数是 ;
观察下列语句,你能得出什么结论?
6的相反数是6;
3.9的相反数是3.9;
100的相反数是100.
8的相反数是8 ;
0的相反数是0.
的相反数是 ;
的相反数是 .
正数的相反数是负数;
负数的相反数是正数;
0的相反数是0.
所有的数
都有相反数
一般地,a的相反数记作 a.这里a表示任意一个数,它可以是正数、负数或者0.
求a的相反数就在a前面添“-”
观察思考
+8
( )
8
+100
100
8
= +8
3.9
= +3.9
试着化简下列式子:
= +
( )
( )
( )
( )
( )
双重符号化简,同号得正,异号得负.
+8的相反数
8的相反数
在任意一个数前面添上“ ”号,所得的数就是原数的相反数.
拓展
简化符号:
( 3) =____; (+0.73)=______;
0=______; ( 34)=_____;
+( 7)=_____.
3
0.73
0
34
7
(+a)= a
( a)= a
+(+a)= a
+( a)= a
“+”可省略
双重符号化简,
异号得负.
同号得正,
练一练
【例1】写出下列各数的相反数:
3, 7, 2.1, , ,0,20.
解:3的相反数是 3, 7的相反数是7, 2.1的相反数是2.1, 的相反数是 , 的相反数是 ,0
的相反数是0,20的相反数是 20.
典型例题
【例2】简化符号:
( 6) =_____;
(+6)=______;
+( 6) =_____;
+(+6)=______.
6
6
6
6
双重符号化简,
异号得负.
同号得正,
1.下列说法正确的是( )
A.带“+”和带“ ”的数互为相反数;
B.数轴上原点两侧的两个点表示的数是相反数;
C.a的相反数是负数;
D.相反数是本身的数只有0.
D
当堂检测
2.填空:
(1) 2.8是 的相反数, 的相反数是3.2;
(2) (+4)是 的相反数, ( 7) 是 的相反数;
(3) (+8)= , ( 9) = .
2.8
3.2
4
7
8
9
3.简化符号:
[+( 6)]=_____;
[ ( 6)]=_____;
{ [ (+6)]}=_____.
选做
在任意一个数前面添上“ ”号,所得的数就是原数的相反数.多重符号从里往外化简即可.
分析
6
6
6
多重符号化简:
“-”有奇数个,结果有“-”
“-”有偶数个,结果无“-”
课堂小结
相反数
一般地,设 a 是一个正数,数轴上与原点的距离是 a 的点有___个,它们分别在正、负半轴上,表示____和_____,这两个数只有______不同.
只有____不同的两个数,互为相反数.
a 的相反数是___;
0 的相反数是___.
符号
符号
0
a
-a
两
-a
-a a
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
