1.4.1 有理数的加法 课件(共35张PPT) 2024-2025学年数学沪科版(2024)七年级上册
文档属性
| 名称 | 1.4.1 有理数的加法 课件(共35张PPT) 2024-2025学年数学沪科版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 20:28:50 | ||
图片预览






文档简介
(共35张PPT)
1.4.1 有理数的加法
1.4 有理数的加减
1.了解有理数加法的意义,理解有理数加法法则的合理性;
2. 能运用该法则准确进行有理数的加法运算.
3.经历计算过程会描述加法运算律,并能熟练应用加法运算律简化计算.
学习目标
1.小学学过的加法类型是正数与正数相加、正数与0相加.
2.引入负数后,加法的类型还有哪几种呢?
例如:(+5)+(+3)= .
5 + 0 = .
8
5
负数与负数相加、
负数与正数相加、
负数与0相加.
引入负数后,如何进行加法运算呢?
新课导入
探究: 一间0℃冷藏室连续两次改变温度.
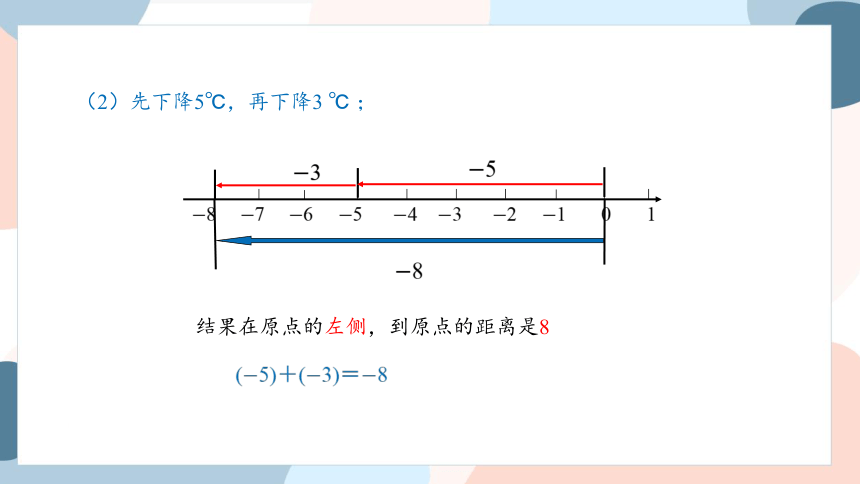
(2)先下降5℃,再下降3 ℃ ;
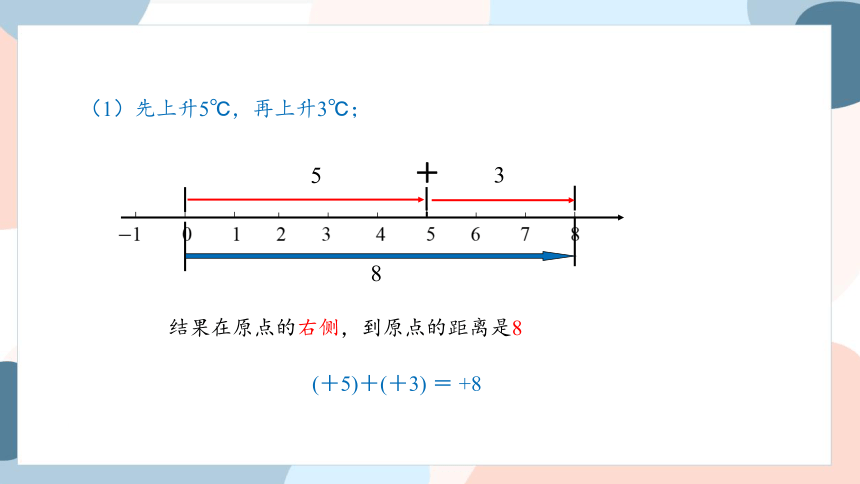
(1)先上升5℃,再上升3℃;
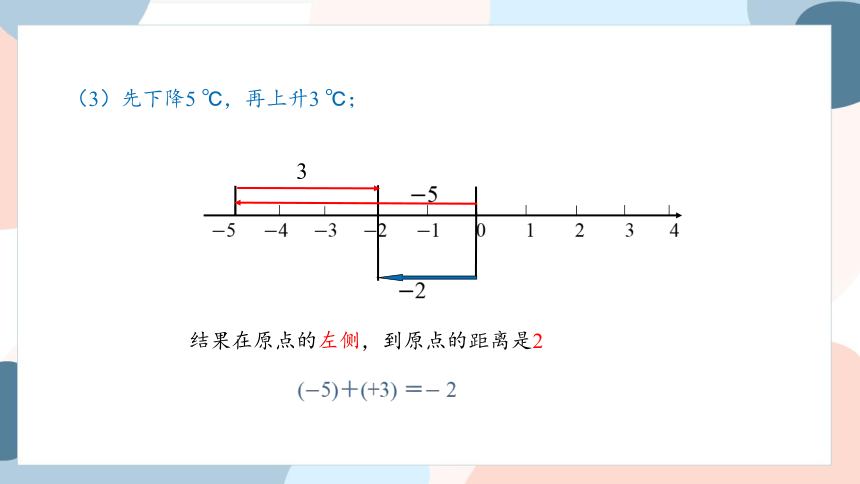
(3)先下降5 ℃ ,再上升3 ℃ ;
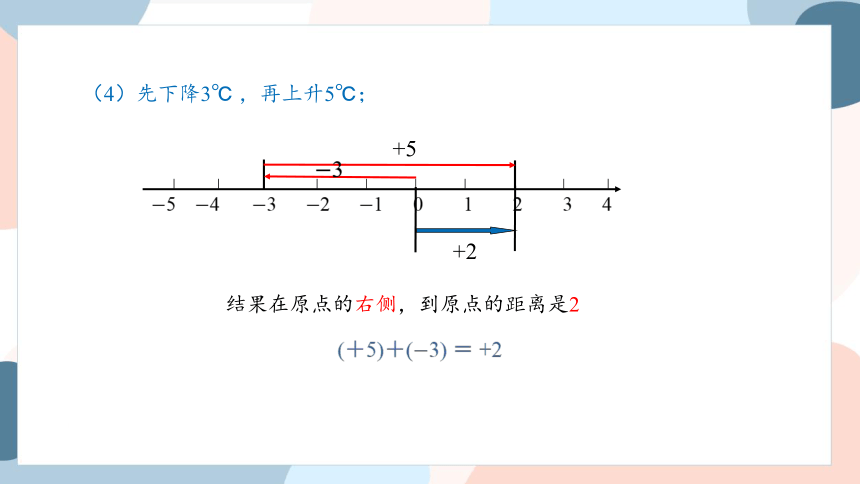
(4)先下降3 ℃ ,再上升5 ℃ ;
把温度上升记作正,温度下降记作负,在数轴上表示连续两次温度变化的总结果,并写出算式.
探索 1:有理数的加法法则
探究新知
(+5)+(+3) = +8
1 0 1 2 3 4 5 6 7 8
5
3
+
8
(1)先上升5℃,再上升3℃;
结果在原点的右侧,到原点的距离是8
(5)+(3)=8
8
8 7 6 5 4 3 2 1 0 1
5
3
(2)先下降5℃,再下降3 ℃ ;
结果在原点的左侧,到原点的距离是8
(5)+(+3) = 2
2
5 4 3 2 1 0 1 2 3 4
5
3
(3)先下降5 ℃,再上升3 ℃;
结果在原点的左侧,到原点的距离是2
(+5)+(3) = +2
结果在原点的右侧,到原点的距离是2
(4)先下降3℃ ,再上升5℃;
5 4 3 2 1 0 1 2 3 4
3
+5
+2
(5)+(+5)=0
5 4 3 2 1 0 1 2 3 4
5
+5
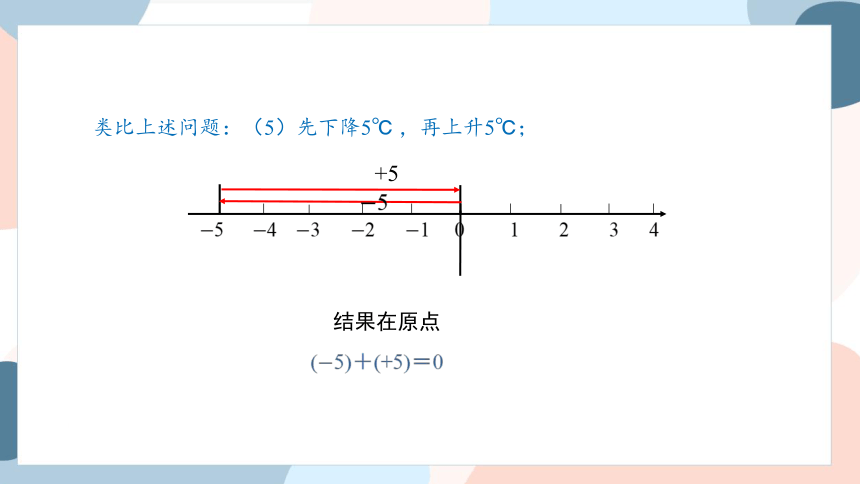
类比上述问题:(5)先下降5℃ ,再上升5℃;
结果在原点
(5)+0=5
5 4 3 2 1 0 1 2 3 4
5
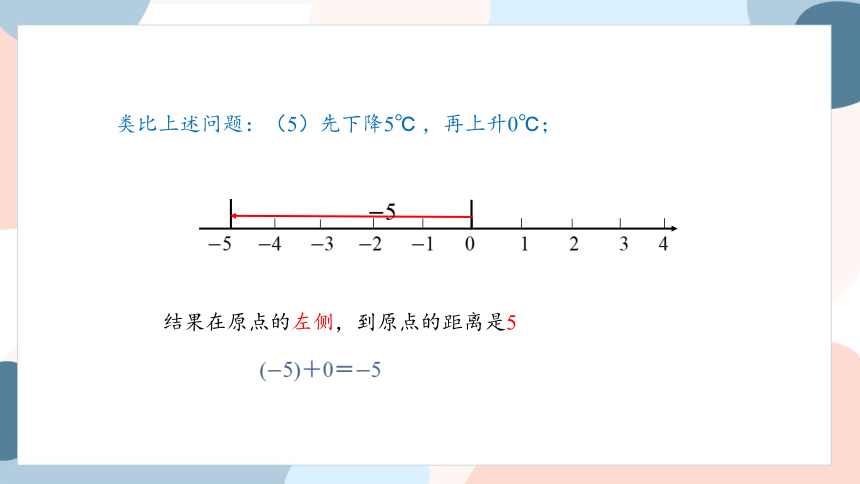
类比上述问题:(5)先下降5℃ ,再上升0℃;
结果在原点的左侧,到原点的距离是5
1. 5 + 3 =
2.(5)+(3)=
同号两数相加
3. 5+(3)=
4. 3+(5)=
5. 5+(5)=
异号两数相加
6.(5)+0=
一数和零相加
8
8
2
2
0
5
(1)同号两数相加,取加数的符号,并把绝对值相加.
(2)异号两数相加,绝对值不相等时,取绝对值较大的加数的符号,
并用较大的绝对值减去较小的绝对值.
绝对值相等时和为0.
(3)一个数与0相加,仍得这个数.
注意:1.确定和的符号;
2.确定和的绝对值.
有理数的加法法则
归纳总结
例1:计算:
(2) ;
(1) ;
(4).
解:(1)
(2)
(4)
(3)
(3)
典型例题
有理数加法运算的基本步骤:
1.先判断类型(同号、异号等);
2.再确定和的符号;
3.最后进行绝对值的加减运算.
归纳总结
(1);
(2).
解: (1)
(2)
例2:计算:
注意:互为相反数的两个数相加得0
典型例题
加数 加数 和的组成 和
符号 绝对值
填表:
练一练
我们以前学过哪些加法的运算律?
两个数相加,交换加数的位置,和不变.
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
加法交换律
加法结合律
这些运算律在有理数范围内还成立吗?
探索 2:有理数的加法运算律
探究新知
问题1:计算:
(1)
(2)
上面各题中计算结果相同吗?换一些数试试.
(2)
(1)
一般地,有理数的加法中,两个数相加,交换加数的位置,和不变.
加法交换律
归纳总结
问题2:计算:
(1)
(2)
上面各题中计算结果相同吗?换一些数试试.
(1)
(2)
探究新知
一般地,有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
加法结合律
归纳总结
例3:计算:
加法交换律和结合律
解:
第一步运算的依据是什么?
探究新知
1.运用了加法的 律.
2.运用了加法的 律.
3.计算的结果是( )
A. B.
C. D.
交换
3
结合
B
练一练
例4:某生态农业公司应用现代技术手段,加强对品牌酥梨的全产业管理,探索数字农业发展新模式.现对一种热销的酥梨逐个称重,超过标准质量(300g)的用正数表示,不足的用负数表示,其中1盒12个酥梨的检测结果如下表:
样品编号 1 2 3 4 5 6 7 8 9 10 11 12
与标准质量的差/g +50 +10
求这盒酥梨的总质量.
探索 3:有理数加法的应用
典型例题
解:
即这盒酥梨的总质量为g.
样品编号 1 2 3 4 5 6 7 8 9 10 11 12
与标准质量的差/g +50 +10
某村共有6块小麦试验田,每块试验田今年的收成与去年相比情况如下,增产为正,减产为负. (单位:kg)
今年的小麦总产量与去年相比情况如何?
解:
答:今年的小麦总产量与去年相比,增产了
练一练
1. 是应用了( )
A.加法交换律 B.加法结合律
C.分配律 D.加法交换律与结合律
D
习题1
当堂检测
2.对于两个有理数的和,下列说法正确的是( )
A.一定比任何一个有理数大
B.至少比其中一个有理数大
C.一定比任何一个有理数小
D.以上说法都不正确
D
习题2
3.八年级某班班费收支情况如下(收入为正):
,该班期末时班费结余为( )
A.82元 B.85元 C.35元 D.92元
A
习题3
4.计算:
(1)
解:(1)
同号的两个数先加
习题4
4.计算:
(2)
解:(2)
互为相反数的两个数先加
4.计算:
(3)
解:(3)
能凑整的数先计算
4.计算:
(4)
解:(4)
同分母分数先加
确定类型 定符号 绝对值
同号
异号(绝对值不相等)
异号(互为相反数) 与0相加 相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
有理数的加法法则:
课堂总结
有理数的加法
加法法则
应用
加法结合律:
加法交换律:
加法运算律
基本步骤
2.再确定和的符号;
1.先判断类型(同号、异号等);
3.最后进行绝对值的加减运算.
1.4.1 有理数的加法
1.4 有理数的加减
1.了解有理数加法的意义,理解有理数加法法则的合理性;
2. 能运用该法则准确进行有理数的加法运算.
3.经历计算过程会描述加法运算律,并能熟练应用加法运算律简化计算.
学习目标
1.小学学过的加法类型是正数与正数相加、正数与0相加.
2.引入负数后,加法的类型还有哪几种呢?
例如:(+5)+(+3)= .
5 + 0 = .
8
5
负数与负数相加、
负数与正数相加、
负数与0相加.
引入负数后,如何进行加法运算呢?
新课导入
探究: 一间0℃冷藏室连续两次改变温度.
(2)先下降5℃,再下降3 ℃ ;
(1)先上升5℃,再上升3℃;
(3)先下降5 ℃ ,再上升3 ℃ ;
(4)先下降3 ℃ ,再上升5 ℃ ;
把温度上升记作正,温度下降记作负,在数轴上表示连续两次温度变化的总结果,并写出算式.
探索 1:有理数的加法法则
探究新知
(+5)+(+3) = +8
1 0 1 2 3 4 5 6 7 8
5
3
+
8
(1)先上升5℃,再上升3℃;
结果在原点的右侧,到原点的距离是8
(5)+(3)=8
8
8 7 6 5 4 3 2 1 0 1
5
3
(2)先下降5℃,再下降3 ℃ ;
结果在原点的左侧,到原点的距离是8
(5)+(+3) = 2
2
5 4 3 2 1 0 1 2 3 4
5
3
(3)先下降5 ℃,再上升3 ℃;
结果在原点的左侧,到原点的距离是2
(+5)+(3) = +2
结果在原点的右侧,到原点的距离是2
(4)先下降3℃ ,再上升5℃;
5 4 3 2 1 0 1 2 3 4
3
+5
+2
(5)+(+5)=0
5 4 3 2 1 0 1 2 3 4
5
+5
类比上述问题:(5)先下降5℃ ,再上升5℃;
结果在原点
(5)+0=5
5 4 3 2 1 0 1 2 3 4
5
类比上述问题:(5)先下降5℃ ,再上升0℃;
结果在原点的左侧,到原点的距离是5
1. 5 + 3 =
2.(5)+(3)=
同号两数相加
3. 5+(3)=
4. 3+(5)=
5. 5+(5)=
异号两数相加
6.(5)+0=
一数和零相加
8
8
2
2
0
5
(1)同号两数相加,取加数的符号,并把绝对值相加.
(2)异号两数相加,绝对值不相等时,取绝对值较大的加数的符号,
并用较大的绝对值减去较小的绝对值.
绝对值相等时和为0.
(3)一个数与0相加,仍得这个数.
注意:1.确定和的符号;
2.确定和的绝对值.
有理数的加法法则
归纳总结
例1:计算:
(2) ;
(1) ;
(4).
解:(1)
(2)
(4)
(3)
(3)
典型例题
有理数加法运算的基本步骤:
1.先判断类型(同号、异号等);
2.再确定和的符号;
3.最后进行绝对值的加减运算.
归纳总结
(1);
(2).
解: (1)
(2)
例2:计算:
注意:互为相反数的两个数相加得0
典型例题
加数 加数 和的组成 和
符号 绝对值
填表:
练一练
我们以前学过哪些加法的运算律?
两个数相加,交换加数的位置,和不变.
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
加法交换律
加法结合律
这些运算律在有理数范围内还成立吗?
探索 2:有理数的加法运算律
探究新知
问题1:计算:
(1)
(2)
上面各题中计算结果相同吗?换一些数试试.
(2)
(1)
一般地,有理数的加法中,两个数相加,交换加数的位置,和不变.
加法交换律
归纳总结
问题2:计算:
(1)
(2)
上面各题中计算结果相同吗?换一些数试试.
(1)
(2)
探究新知
一般地,有理数的加法中,三个数相加,先把前两个数相加,或者先把后两个数相加,和不变.
加法结合律
归纳总结
例3:计算:
加法交换律和结合律
解:
第一步运算的依据是什么?
探究新知
1.运用了加法的 律.
2.运用了加法的 律.
3.计算的结果是( )
A. B.
C. D.
交换
3
结合
B
练一练
例4:某生态农业公司应用现代技术手段,加强对品牌酥梨的全产业管理,探索数字农业发展新模式.现对一种热销的酥梨逐个称重,超过标准质量(300g)的用正数表示,不足的用负数表示,其中1盒12个酥梨的检测结果如下表:
样品编号 1 2 3 4 5 6 7 8 9 10 11 12
与标准质量的差/g +50 +10
求这盒酥梨的总质量.
探索 3:有理数加法的应用
典型例题
解:
即这盒酥梨的总质量为g.
样品编号 1 2 3 4 5 6 7 8 9 10 11 12
与标准质量的差/g +50 +10
某村共有6块小麦试验田,每块试验田今年的收成与去年相比情况如下,增产为正,减产为负. (单位:kg)
今年的小麦总产量与去年相比情况如何?
解:
答:今年的小麦总产量与去年相比,增产了
练一练
1. 是应用了( )
A.加法交换律 B.加法结合律
C.分配律 D.加法交换律与结合律
D
习题1
当堂检测
2.对于两个有理数的和,下列说法正确的是( )
A.一定比任何一个有理数大
B.至少比其中一个有理数大
C.一定比任何一个有理数小
D.以上说法都不正确
D
习题2
3.八年级某班班费收支情况如下(收入为正):
,该班期末时班费结余为( )
A.82元 B.85元 C.35元 D.92元
A
习题3
4.计算:
(1)
解:(1)
同号的两个数先加
习题4
4.计算:
(2)
解:(2)
互为相反数的两个数先加
4.计算:
(3)
解:(3)
能凑整的数先计算
4.计算:
(4)
解:(4)
同分母分数先加
确定类型 定符号 绝对值
同号
异号(绝对值不相等)
异号(互为相反数) 与0相加 相同符号
取绝对值较大的加数的符号
相加
相减
结果是0
仍是这个数
有理数的加法法则:
课堂总结
有理数的加法
加法法则
应用
加法结合律:
加法交换律:
加法运算律
基本步骤
2.再确定和的符号;
1.先判断类型(同号、异号等);
3.最后进行绝对值的加减运算.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
