1.5.2 有理数的乘法运算律 课件(共17张PPT) 2024-2025学年数学沪科版(2024)七年级上册
文档属性
| 名称 | 1.5.2 有理数的乘法运算律 课件(共17张PPT) 2024-2025学年数学沪科版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 225.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 20:32:32 | ||
图片预览




文档简介
(共17张PPT)
1.5 课时2 有理数的乘法运算律
第一章 有理数
学习目标
巩固有理数的乘法运算法则,熟练地进行有理数的乘法运算.
经历探索多个有理数相乘时积的符号变化的过程,培养学生观察能力、运算能力和归纳能力.
通过探索过程树立学生学习数学的自信心,培养学生严谨的数学思维习惯.
复习旧知
有理数的乘法法则是什么?
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与0相乘仍得0.
有理数的乘法法则
例:
( 2) 3 6
2 0 0
( 2) 0 0
( 2) 2 4
( 2) ( 3) 6
2 3 6
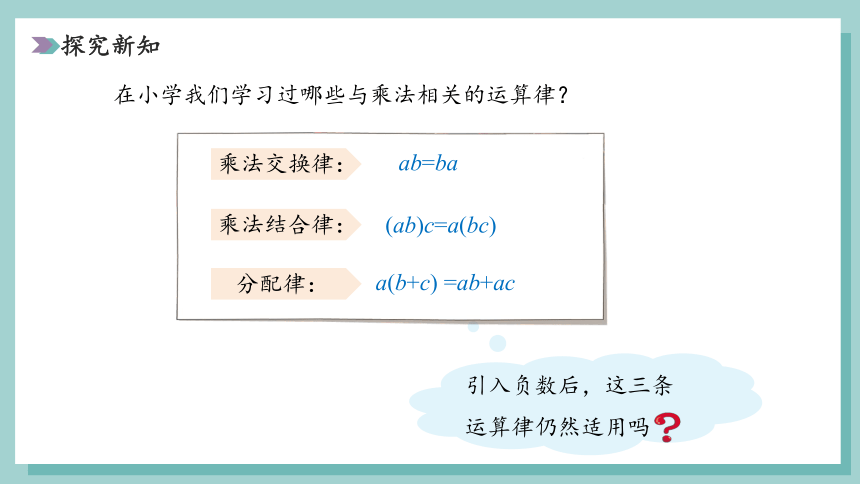
探究新知
在小学我们学习过哪些与乘法相关的运算律?
引入负数后,这三条运算律仍然适用吗
乘法交换律:
ab=ba
乘法结合律:
(ab)c=a(bc)
分配律:
a(b+c) =ab+ac
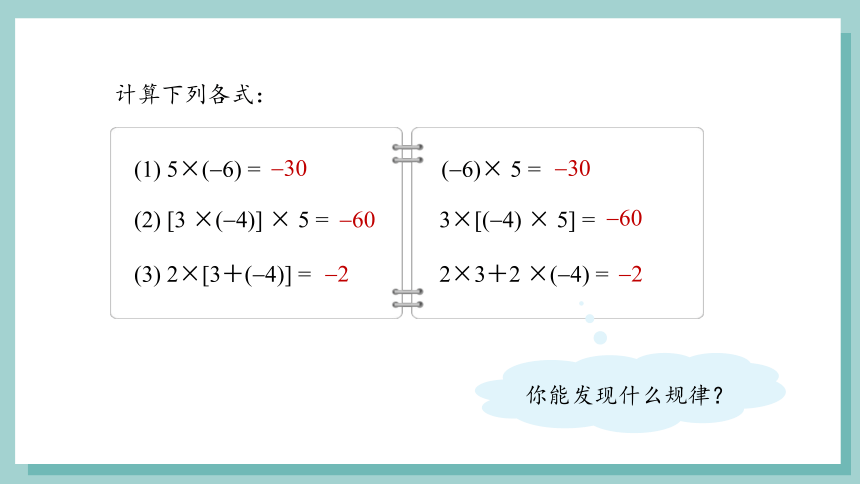
计算下列各式:
(1) 5×( 6) = ( 6)× 5 =
30
30
(3) 2×[3+( 4)] = 2×3+2 ×( 4) =
60
2
2
(2) [3 ×( 4)] × 5 = 3×[( 4) × 5] =
60
你能发现什么规律?
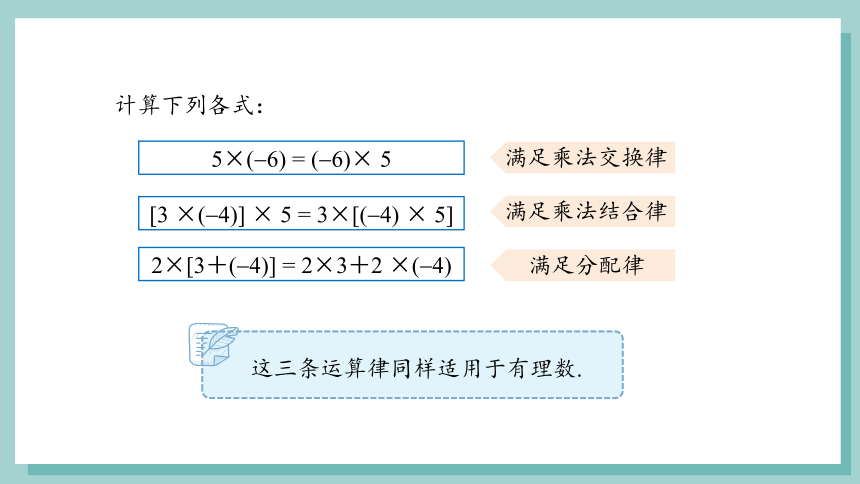
计算下列各式:
这三条运算律同样适用于有理数.
5×( 6) = ( 6)× 5
2×[3+( 4)] = 2×3+2 ×( 4)
[3 ×( 4)] × 5 = 3×[( 4) × 5]
满足乘法交换律
满足乘法结合律
满足分配律
典型例题
例1 计算
解:(1)原式=
(分配律)
= 1
= ( 3) + ( 2) ( 6)
运用运算律有时可以化简计算
合作探究
两个有理数相乘的一般步骤是什么?
有理数乘法的步骤:
确定积的符号;
求绝对值的乘积.
1
2
多个有理数相乘时,应该如何运算呢?
思考
计算下列各式:
(1) ( 4)×5×( 0.25)= ;
(2) ( )×( 16)×(+0.5)×( 4)= ;
(3) (+2)×( 8.5)×( 100)×0×(+90) = .
20
×( 0.25)
5
12
0
多个有理数相乘,可以把它们按顺序依次相乘.
多个有理数相乘,有一个因数为0时,积是多少?
因数都不为0时,积的符号怎样确定?
(1) ( 4)×5×( 0.25)= ;
(2) ( )×( 16)×(+0.5)×( 4)= ;
(3) (+2)×( 8.5)×( 100)×0×(+90) = .
5
12
0
思考
观察积的符号与负因数的个数之间的关系
+
小组活动:
两人一组,其中一名同学随机写出多个有理数的乘法,另外一名同学说出积的符号,最后一起交流积的符号与负因数的个数的关系.
归纳
几个数相乘,有一个因数为0时,积为0.
几个不为0的数相乘,积的符号由负因数的个数决定.
当负因数有奇数个时,积为负;
当负因数有偶数个时,积为正.
1
2
奇负偶正
练习
判断下列各式的积是正的还是负的
2×3×4×( 5)
2×3×( 4)×( 5)
2×( 3)×( 4)×( 5)
( 2)×( 3)×( 4)×( 5)
负
正
负
正
随堂练习
1. (1)如果a<0,b>0,c<0,那么abc_____0;
(2)如果a<0,b<0,c>0,d<0,那么abcd____0;
>
<
解:(1)原式= 8×( 1)×( 3)
2.计算
(1) 2×4×( 1)×( 3)
(2)
= 8×( 3)
= 24
(2)原式=
3.如果abc=0,那么一定有 ( )
A.a=b=0
B.a=0,b≠0,c≠0
C.a,b,c中至少有一个为0
D.a,b,c中最多有一个为0
C
课堂总结
运算律:
乘法交换律:ab=ba.
乘法结合律:(ab)c=a(bc).
分配律:a(b+c)=ab+ac.
多个有理数相乘:
含0的乘法:
几个数相乘,有一个因数为0时,积为0.
(2)不含0的乘法:
几个不为0的数相乘,积的符号由负因数的个数决定.
有理数的乘法运算律
当负因数有奇数个时,积为负;
当负因数有偶数个时,积为正.
奇负偶正
1.5 课时2 有理数的乘法运算律
第一章 有理数
学习目标
巩固有理数的乘法运算法则,熟练地进行有理数的乘法运算.
经历探索多个有理数相乘时积的符号变化的过程,培养学生观察能力、运算能力和归纳能力.
通过探索过程树立学生学习数学的自信心,培养学生严谨的数学思维习惯.
复习旧知
有理数的乘法法则是什么?
两数相乘,同号得正,异号得负,并把绝对值相乘.
任何数与0相乘仍得0.
有理数的乘法法则
例:
( 2) 3 6
2 0 0
( 2) 0 0
( 2) 2 4
( 2) ( 3) 6
2 3 6
探究新知
在小学我们学习过哪些与乘法相关的运算律?
引入负数后,这三条运算律仍然适用吗
乘法交换律:
ab=ba
乘法结合律:
(ab)c=a(bc)
分配律:
a(b+c) =ab+ac
计算下列各式:
(1) 5×( 6) = ( 6)× 5 =
30
30
(3) 2×[3+( 4)] = 2×3+2 ×( 4) =
60
2
2
(2) [3 ×( 4)] × 5 = 3×[( 4) × 5] =
60
你能发现什么规律?
计算下列各式:
这三条运算律同样适用于有理数.
5×( 6) = ( 6)× 5
2×[3+( 4)] = 2×3+2 ×( 4)
[3 ×( 4)] × 5 = 3×[( 4) × 5]
满足乘法交换律
满足乘法结合律
满足分配律
典型例题
例1 计算
解:(1)原式=
(分配律)
= 1
= ( 3) + ( 2) ( 6)
运用运算律有时可以化简计算
合作探究
两个有理数相乘的一般步骤是什么?
有理数乘法的步骤:
确定积的符号;
求绝对值的乘积.
1
2
多个有理数相乘时,应该如何运算呢?
思考
计算下列各式:
(1) ( 4)×5×( 0.25)= ;
(2) ( )×( 16)×(+0.5)×( 4)= ;
(3) (+2)×( 8.5)×( 100)×0×(+90) = .
20
×( 0.25)
5
12
0
多个有理数相乘,可以把它们按顺序依次相乘.
多个有理数相乘,有一个因数为0时,积是多少?
因数都不为0时,积的符号怎样确定?
(1) ( 4)×5×( 0.25)= ;
(2) ( )×( 16)×(+0.5)×( 4)= ;
(3) (+2)×( 8.5)×( 100)×0×(+90) = .
5
12
0
思考
观察积的符号与负因数的个数之间的关系
+
小组活动:
两人一组,其中一名同学随机写出多个有理数的乘法,另外一名同学说出积的符号,最后一起交流积的符号与负因数的个数的关系.
归纳
几个数相乘,有一个因数为0时,积为0.
几个不为0的数相乘,积的符号由负因数的个数决定.
当负因数有奇数个时,积为负;
当负因数有偶数个时,积为正.
1
2
奇负偶正
练习
判断下列各式的积是正的还是负的
2×3×4×( 5)
2×3×( 4)×( 5)
2×( 3)×( 4)×( 5)
( 2)×( 3)×( 4)×( 5)
负
正
负
正
随堂练习
1. (1)如果a<0,b>0,c<0,那么abc_____0;
(2)如果a<0,b<0,c>0,d<0,那么abcd____0;
>
<
解:(1)原式= 8×( 1)×( 3)
2.计算
(1) 2×4×( 1)×( 3)
(2)
= 8×( 3)
= 24
(2)原式=
3.如果abc=0,那么一定有 ( )
A.a=b=0
B.a=0,b≠0,c≠0
C.a,b,c中至少有一个为0
D.a,b,c中最多有一个为0
C
课堂总结
运算律:
乘法交换律:ab=ba.
乘法结合律:(ab)c=a(bc).
分配律:a(b+c)=ab+ac.
多个有理数相乘:
含0的乘法:
几个数相乘,有一个因数为0时,积为0.
(2)不含0的乘法:
几个不为0的数相乘,积的符号由负因数的个数决定.
有理数的乘法运算律
当负因数有奇数个时,积为负;
当负因数有偶数个时,积为正.
奇负偶正
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
