1.6 课时2 科学记数法 课件(共15张PPT) 2024-2025学年数学沪科版(2024)七年级上册
文档属性
| 名称 | 1.6 课时2 科学记数法 课件(共15张PPT) 2024-2025学年数学沪科版(2024)七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 20:39:19 | ||
图片预览




文档简介
(共15张PPT)
第一章 有理数
1.6 课时2 科学记数法
1.经历了实际生活中大数的存在,从而了解科学记数法的意义.
2.学会用科学记数法表示绝对值大于10的数.
3.借助身边熟悉的事物进一步体会,感受生活中的大数,增强数感.
4.经历了科学记数法的学习,感受用科学记数法表示大数带来的方便,鼓励学生独立思考、实践意识,进一步培养学生创意思维.
学习目标
三亿
六十九万六千
七十亿
新课导入
新课导入
长江三峡水库容量达
39 300 000 000 m3.
光在空气中的传播速度大约是
300 000 000 m/s.
这样大的数读、写都不方便,有没有简单的方法表示大数呢?
3930百万
3亿
还有其他的表示方法吗?
交流
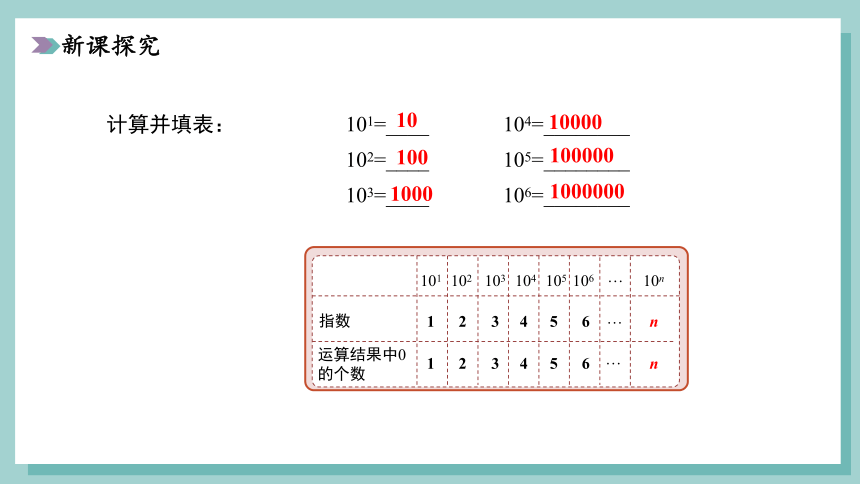
计算并填表:
指数
运算结果中0
的个数
101
102
103
104
105
106
…
10n
…
…
1
2
3
4
5
6
n
101=____
102=____
103=____
104=________
105=________
106=________
10
100
1000
10000
100000
1000000
1
2
3
4
5
6
n
新课探究
通过上面的规律填空
(1)300000000=3×( )=3×10( );
(2)39300000000=393×( )=3.93×( )
=3.93×10( );
(3) 6100000000=61×( )=6.1×( )
=6.1×10( ).
100000000
8
100000000
10000000000
10
100000000
1000000000
9
观察乘号前面的数,找到共同特征:
大于1小于10的数
一般地,一个绝对值大于10的数都可记成±a×10n的形式,其中1≤a<10.
思考
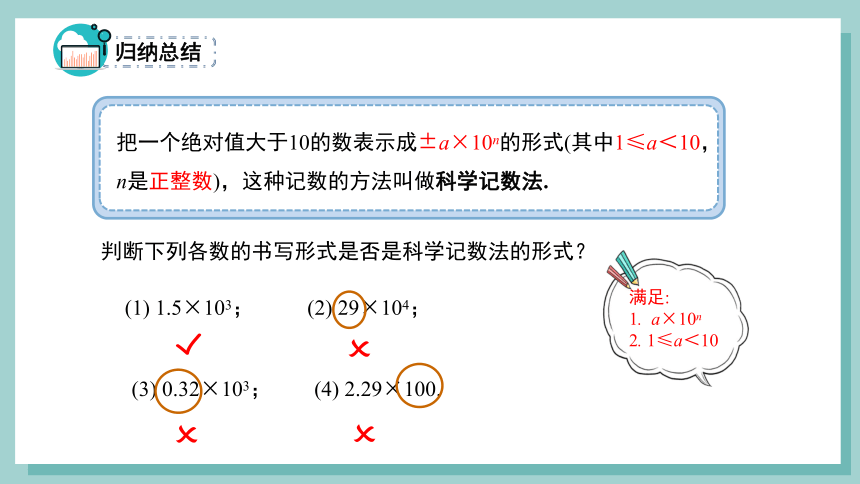
把一个绝对值大于10的数表示成±a×10n的形式(其中1≤a<10,n是正整数),这种记数的方法叫做科学记数法.
(1) 1.5×103; (2) 29×104;
(3) 0.32×103; (4) 2.29×100.
判断下列各数的书写形式是否是科学记数法的形式?
满足:
1. a×10n
2. 1≤a<10
归纳总结
例1 用科学记数法表示下列各数:
1000000
(2) 57000000
(3)–123000000000
=106
=1×106
解:(1) 1000000
(2) 57000000
=5.7×107
(3)–123000000000
= 1.23×1011
用科学记数法表示负数时,先写出它的相反数的形式,再添加负号.
–
读作“1乘10的6次方(幂)”
读作“5.7乘10的7次方(幂)”
读作“负的1.23乘10的11次方(幂)”
典型例题
(1)1000000=1.0×106
(2) 57000000=5.7×107
(3) –123000000000= –1.23×1011
上面的式子中,等号左边整数的位数与右边10的指数有什么关系?用科学记数法表示一个n位整数,其中10的指数是______.
1000000
等号左边的数
57000000
–123000000000
等号右边10的指数
6
7
11
等号左边的数的位数
7
8
12
– 1
– 1
– 1
n –1
右边10的指数等于左边整数的位数减1
思考
第一步:确定a (1≤a<10)
去掉末尾的0,其余部分中,把小数点添加(或移动)到最高位数的后面,得到的数为a.
第二步:确定n (n为正整数)
n为原数的整数位数减去1.
用科学记数法表示数的步骤:
归纳总结
例2 《2020年全球森林资源评估》报告指出:1990年以来,全球因砍伐而丧失了约4.2亿公顷森林,但森林丧失的速度已大幅下降,2015至2020年,每年因砍伐而丧失的森林面积约为1000万共顷.请用科学记数法表示4.2亿和1000万.
解:
4.2亿=420 000 000=4.2×108.
1000万=10 000 000=4×107
典型例题
1. 用科学记数法表示下列各数:
10000,800000,56000000,7400000.
解:10000=104.
800000=8×105.
56000000=5.6×107.
7400000=7.4×106.
当堂检测
2.下列用科学记数法表示的数原来各是什么数?
1×107,4×103,8.5×106,7.04×105.
解:1×107
4×103
8.5×106
7.04×105
= 10000000.
= 4×1000
= 4000.
= 8.5×1000000
= 8500000.
= 7.04×100000
= 704000.
将a×10n表示的数还原时,a中小数点向右移动n位,位数不够0来凑.
3. 截止2022年12月31日,中国共产党党员总数为9804.1万名.用科学记数法表示9804.1万.
9804.1万用科学记数法表示:
解:
98 041 000
9.8041×107.
科学记数法
概念:
步骤:
第二步:确定n (n为正整数),n为原数的整数位数减去1.
第一步:确定a (1≤a<10),去掉末尾的0,其余部分中,把小数点添加(或移动)到最高位数的后面,得到的数为a.
还原数:
a中小数点向右移动n位,位数不够0来凑
把一个绝对值大于10的数表示成±a×10n的形式(其中1≤a<10,n是正整数),这种记数的方法叫做科学记数法.
课堂小结
第一章 有理数
1.6 课时2 科学记数法
1.经历了实际生活中大数的存在,从而了解科学记数法的意义.
2.学会用科学记数法表示绝对值大于10的数.
3.借助身边熟悉的事物进一步体会,感受生活中的大数,增强数感.
4.经历了科学记数法的学习,感受用科学记数法表示大数带来的方便,鼓励学生独立思考、实践意识,进一步培养学生创意思维.
学习目标
三亿
六十九万六千
七十亿
新课导入
新课导入
长江三峡水库容量达
39 300 000 000 m3.
光在空气中的传播速度大约是
300 000 000 m/s.
这样大的数读、写都不方便,有没有简单的方法表示大数呢?
3930百万
3亿
还有其他的表示方法吗?
交流
计算并填表:
指数
运算结果中0
的个数
101
102
103
104
105
106
…
10n
…
…
1
2
3
4
5
6
n
101=____
102=____
103=____
104=________
105=________
106=________
10
100
1000
10000
100000
1000000
1
2
3
4
5
6
n
新课探究
通过上面的规律填空
(1)300000000=3×( )=3×10( );
(2)39300000000=393×( )=3.93×( )
=3.93×10( );
(3) 6100000000=61×( )=6.1×( )
=6.1×10( ).
100000000
8
100000000
10000000000
10
100000000
1000000000
9
观察乘号前面的数,找到共同特征:
大于1小于10的数
一般地,一个绝对值大于10的数都可记成±a×10n的形式,其中1≤a<10.
思考
把一个绝对值大于10的数表示成±a×10n的形式(其中1≤a<10,n是正整数),这种记数的方法叫做科学记数法.
(1) 1.5×103; (2) 29×104;
(3) 0.32×103; (4) 2.29×100.
判断下列各数的书写形式是否是科学记数法的形式?
满足:
1. a×10n
2. 1≤a<10
归纳总结
例1 用科学记数法表示下列各数:
1000000
(2) 57000000
(3)–123000000000
=106
=1×106
解:(1) 1000000
(2) 57000000
=5.7×107
(3)–123000000000
= 1.23×1011
用科学记数法表示负数时,先写出它的相反数的形式,再添加负号.
–
读作“1乘10的6次方(幂)”
读作“5.7乘10的7次方(幂)”
读作“负的1.23乘10的11次方(幂)”
典型例题
(1)1000000=1.0×106
(2) 57000000=5.7×107
(3) –123000000000= –1.23×1011
上面的式子中,等号左边整数的位数与右边10的指数有什么关系?用科学记数法表示一个n位整数,其中10的指数是______.
1000000
等号左边的数
57000000
–123000000000
等号右边10的指数
6
7
11
等号左边的数的位数
7
8
12
– 1
– 1
– 1
n –1
右边10的指数等于左边整数的位数减1
思考
第一步:确定a (1≤a<10)
去掉末尾的0,其余部分中,把小数点添加(或移动)到最高位数的后面,得到的数为a.
第二步:确定n (n为正整数)
n为原数的整数位数减去1.
用科学记数法表示数的步骤:
归纳总结
例2 《2020年全球森林资源评估》报告指出:1990年以来,全球因砍伐而丧失了约4.2亿公顷森林,但森林丧失的速度已大幅下降,2015至2020年,每年因砍伐而丧失的森林面积约为1000万共顷.请用科学记数法表示4.2亿和1000万.
解:
4.2亿=420 000 000=4.2×108.
1000万=10 000 000=4×107
典型例题
1. 用科学记数法表示下列各数:
10000,800000,56000000,7400000.
解:10000=104.
800000=8×105.
56000000=5.6×107.
7400000=7.4×106.
当堂检测
2.下列用科学记数法表示的数原来各是什么数?
1×107,4×103,8.5×106,7.04×105.
解:1×107
4×103
8.5×106
7.04×105
= 10000000.
= 4×1000
= 4000.
= 8.5×1000000
= 8500000.
= 7.04×100000
= 704000.
将a×10n表示的数还原时,a中小数点向右移动n位,位数不够0来凑.
3. 截止2022年12月31日,中国共产党党员总数为9804.1万名.用科学记数法表示9804.1万.
9804.1万用科学记数法表示:
解:
98 041 000
9.8041×107.
科学记数法
概念:
步骤:
第二步:确定n (n为正整数),n为原数的整数位数减去1.
第一步:确定a (1≤a<10),去掉末尾的0,其余部分中,把小数点添加(或移动)到最高位数的后面,得到的数为a.
还原数:
a中小数点向右移动n位,位数不够0来凑
把一个绝对值大于10的数表示成±a×10n的形式(其中1≤a<10,n是正整数),这种记数的方法叫做科学记数法.
课堂小结
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
