1.7 近似数 课件(共20张PPT) 2024-2025学年数学沪科版(2024)七年级上册
文档属性
| 名称 | 1.7 近似数 课件(共20张PPT) 2024-2025学年数学沪科版(2024)七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 511.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 20:40:21 | ||
图片预览








文档简介
(共20张PPT)
1.7 近似数
第一章 有理数
学习目标
理解准确数、近似数的概念,并能辨别它们.
会用四舍五入法按要求取一个数的近似数,能说出一个近似数精确到的位数,培养学生观察能力、运算能力.
通过探索过程树立学生学习数学的自信心,感受数学知识与生活实际的联系.
复习旧知
1.同学们还记得圆周率是用什么表示的吗?我们常用的圆周率是多少?它是一个准确值吗?
2.小学学过的“四舍五入”是什么?
生活中,有的数据无法取到精确数据或没有必要取到精确数据,该怎么办?
探究新知
1.数一数今天班上的同学数.
2.查一查你的数学课本的页数.
3.量一量数学课本的宽度.
4.称一称你的书包的质量.
操作
这些数据中,哪些是精确的,哪些是近似的?
操作1和2的数据由计数得来,是准确数;
操作3和4的数据由测量而来,是近似数.
归纳
由于受测量工具、测量方法、测量者等因素的影响,测量的结果一般只是一个与实际数值很接近的数,我们称此数为近似数.
例如:在涉及有关圆的周长或面积计算时,遇到π,常取π≈3.14.又如黄山的最高峰——莲花峰海拔1864.8m,介绍时常说约1900m,或约1860m.
什么样的数是近似数?
思考
1.我们得不到与实际完全相符的数,而是通过测量、估算得到的数都是近似数.例如,姚明的身高是2.26米.
2.有时我们为了叙述、书写方便,通过四舍五入得到的数也是近似数.例如,2024年全国高考报名的考生共1342万人.
近似数是由测量、称量、估计等等得到的数.近似数一般带有大约、左右、大概等等词语.
说出语句中的准确数和近似数,并和同伴交流数的辨别方法.
1.妈妈去买水果,买了8个苹果,大约3千克.
2.小民与小李买了2瓶水,4根黄瓜,6袋零食,约20元,然后骑车去3.5km外郊游,大约玩了4.5小时回家.
3.我国共有56个民族.
4.举世瞩目的西气东输工程全长4000km.
练数与准确数有什么区别?
思考
准确数是完全符合实际的数.而近似数是一个与实际接近的数.
近似数是一个与准确数接近的数,其接近程度可以用精确度表示.
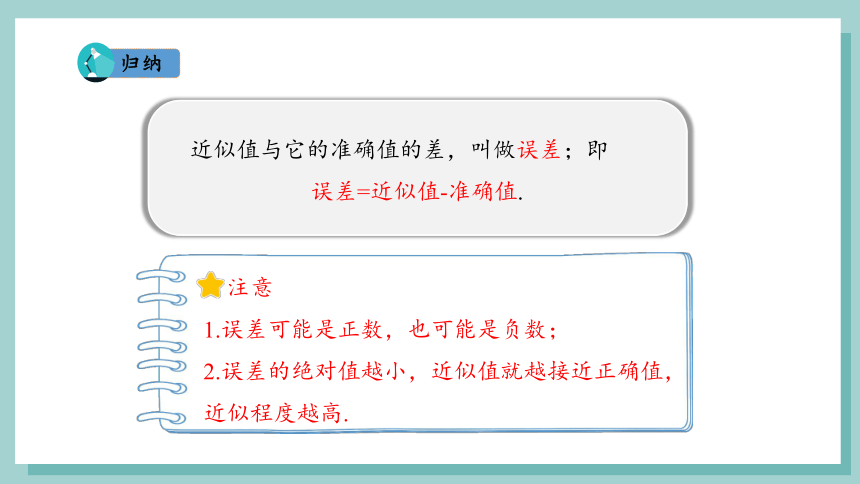
近似值与它的准确值的差,叫做误差;即
误差=近似值-准确值.
注意
1.误差可能是正数,也可能是负数;
2.误差的绝对值越小,近似值就越接近正确值,近似程度越高.
归纳
例如:数学课本的宽度值18.4cm,18.43cm都是近似数,
18.4cm是精确到十分位(或者说精确到0.1cm)的近似数.
18.43cm是精确到百分位(或者说精确到0.01cm)的近似数.
近似数与准确数的接近程度,通常用精确度表示.
精确度由最后一位数字所在的位置确定.
归纳
仿写:按四舍五入法对圆周率π取近似数时,有
π≈3 (精确到个位)
π≈3.1 (精确到0.1或叫做精确到十分位)
π≈3.14 (精确到0.01或叫做精确到百分位)
π≈3.142 (精确到 或叫做精确到 )
π≈3.141 6 (精确到 或叫做精确到 )
……
1 0.1 十分位
4 0.01 百分位
2
6
练习
0.001
千分位
0.0001
万分位
小组讨论:观察上述近似数说说怎么确定一个近似数的精确度?那又是怎么取一个数的近似数?
归纳
1.确定近似数的精确度的方法:看这个近似数的最后一位数字,它在哪个数位上就说明该近似数精确到哪一个数位.
2.取近似数的方法:求一个精确到某一数位的近似数时,对这一数位后面的那个数进行四舍五入.
练习
按要求对下列各数取近似数,并和同伴交流结果.
(1)13.25(精确到个位);(2)1.794(精确到0.1);
(3)1.794(精确到0.01); (4)1 029500(精确到千位).
解:(1)13.25≈13;(2)1.794≈1.8;
(3)1.794≈1.79;(4)1029500=1.0295×106≈1.030×106.
1.小数点最后面的0不能随意添加或删除,否则就改变了近似数的精确度;
2.当数据较大时,其近似值可以用科学记数法表示.
这个0可以省略吗?
典型例题
例1 下列由四舍五入得到的近似数,各精确到哪一位?
(1) 48.3 (2) 0.03086
(3) 2.40万 (4) 6.5×
解:(1)48.3,精确到十分位;
(2)0.03086,精确到十万分位(或精确到0.00001);
(3)2.40万,精确到百位;
(4)6.5× ,精确到千位.
先将其写成原数,再确定其精确度.
先把该数写成单位为“个”的数,再确定其精确度.
例2 第五届中国国际进口博览会意向成交金额达735.2亿美元.会期六天,平均每天达成意向成交金额多少亿美元?(精确到0.1亿美元)
解:平均每天达成意向成交金额为
735.2÷6≈122.53≈122.5(亿美元).
例3 “十一”期间,某商场准备对商品打8折促销.一种原价为348元的微波炉,打折后,如果精确到元,定价是多少?
解:这种微波炉打8折后的价格为
348278.4(元)
精确到元的定价为278元.
2.数4是4.3的近似值,其中4.3叫做真值,若一个数经四舍五入得到的近似数是12,则下列各数中不可能是12的真值的是( )
A. 12.38 B. 12.66 C. 11.99 D. 12.42
随堂练习
1.下列结论正确的是( )
A. 近似数4.230和4.23的精确度是一样的
B. 近似数89.0是精确到个位
C. 近似数0.00510与0.0510的精确度不一样
D. 近似数6万与近似数60 000的精确度相同
C
B
3.下列由四舍五入得到的近似数,各精确到哪一位?
(1)0.00407;(2)1.0;
(3)1.03万; (4)3.90×105.
解:(1)精确到0.00001(或十万分位);
(2)精确到0.1(或十分位);
(3)1.03万=10 300,故精确到百位;
(4)3.90×105=390 000,故精确到千位.
4.用四舍五入法,按括号中的要求对下列各数取近似数.
(1)2.009(精确到0.01); (2)46 854 000(精确到万位);
(3)4.762×107(精确到百万位); (4)13亿(精确到十万位).
解:(1)2.009≈2.01;
(2)46 854 000≈4.685×107;
(3)4.762×107≈4.8×107;
(4)13亿≈1.300 0×109 .
课堂总结
概念:
近似数是一个与实际数值很接近的数.
误差是近似值与它的准确值的差.
精确度表示近似数与准确数的接近程度.
近似数
应用:
判断近似数与准确数.
按照要求取近似数.
由近似数判断其精确度.
1.7 近似数
第一章 有理数
学习目标
理解准确数、近似数的概念,并能辨别它们.
会用四舍五入法按要求取一个数的近似数,能说出一个近似数精确到的位数,培养学生观察能力、运算能力.
通过探索过程树立学生学习数学的自信心,感受数学知识与生活实际的联系.
复习旧知
1.同学们还记得圆周率是用什么表示的吗?我们常用的圆周率是多少?它是一个准确值吗?
2.小学学过的“四舍五入”是什么?
生活中,有的数据无法取到精确数据或没有必要取到精确数据,该怎么办?
探究新知
1.数一数今天班上的同学数.
2.查一查你的数学课本的页数.
3.量一量数学课本的宽度.
4.称一称你的书包的质量.
操作
这些数据中,哪些是精确的,哪些是近似的?
操作1和2的数据由计数得来,是准确数;
操作3和4的数据由测量而来,是近似数.
归纳
由于受测量工具、测量方法、测量者等因素的影响,测量的结果一般只是一个与实际数值很接近的数,我们称此数为近似数.
例如:在涉及有关圆的周长或面积计算时,遇到π,常取π≈3.14.又如黄山的最高峰——莲花峰海拔1864.8m,介绍时常说约1900m,或约1860m.
什么样的数是近似数?
思考
1.我们得不到与实际完全相符的数,而是通过测量、估算得到的数都是近似数.例如,姚明的身高是2.26米.
2.有时我们为了叙述、书写方便,通过四舍五入得到的数也是近似数.例如,2024年全国高考报名的考生共1342万人.
近似数是由测量、称量、估计等等得到的数.近似数一般带有大约、左右、大概等等词语.
说出语句中的准确数和近似数,并和同伴交流数的辨别方法.
1.妈妈去买水果,买了8个苹果,大约3千克.
2.小民与小李买了2瓶水,4根黄瓜,6袋零食,约20元,然后骑车去3.5km外郊游,大约玩了4.5小时回家.
3.我国共有56个民族.
4.举世瞩目的西气东输工程全长4000km.
练数与准确数有什么区别?
思考
准确数是完全符合实际的数.而近似数是一个与实际接近的数.
近似数是一个与准确数接近的数,其接近程度可以用精确度表示.
近似值与它的准确值的差,叫做误差;即
误差=近似值-准确值.
注意
1.误差可能是正数,也可能是负数;
2.误差的绝对值越小,近似值就越接近正确值,近似程度越高.
归纳
例如:数学课本的宽度值18.4cm,18.43cm都是近似数,
18.4cm是精确到十分位(或者说精确到0.1cm)的近似数.
18.43cm是精确到百分位(或者说精确到0.01cm)的近似数.
近似数与准确数的接近程度,通常用精确度表示.
精确度由最后一位数字所在的位置确定.
归纳
仿写:按四舍五入法对圆周率π取近似数时,有
π≈3 (精确到个位)
π≈3.1 (精确到0.1或叫做精确到十分位)
π≈3.14 (精确到0.01或叫做精确到百分位)
π≈3.142 (精确到 或叫做精确到 )
π≈3.141 6 (精确到 或叫做精确到 )
……
1 0.1 十分位
4 0.01 百分位
2
6
练习
0.001
千分位
0.0001
万分位
小组讨论:观察上述近似数说说怎么确定一个近似数的精确度?那又是怎么取一个数的近似数?
归纳
1.确定近似数的精确度的方法:看这个近似数的最后一位数字,它在哪个数位上就说明该近似数精确到哪一个数位.
2.取近似数的方法:求一个精确到某一数位的近似数时,对这一数位后面的那个数进行四舍五入.
练习
按要求对下列各数取近似数,并和同伴交流结果.
(1)13.25(精确到个位);(2)1.794(精确到0.1);
(3)1.794(精确到0.01); (4)1 029500(精确到千位).
解:(1)13.25≈13;(2)1.794≈1.8;
(3)1.794≈1.79;(4)1029500=1.0295×106≈1.030×106.
1.小数点最后面的0不能随意添加或删除,否则就改变了近似数的精确度;
2.当数据较大时,其近似值可以用科学记数法表示.
这个0可以省略吗?
典型例题
例1 下列由四舍五入得到的近似数,各精确到哪一位?
(1) 48.3 (2) 0.03086
(3) 2.40万 (4) 6.5×
解:(1)48.3,精确到十分位;
(2)0.03086,精确到十万分位(或精确到0.00001);
(3)2.40万,精确到百位;
(4)6.5× ,精确到千位.
先将其写成原数,再确定其精确度.
先把该数写成单位为“个”的数,再确定其精确度.
例2 第五届中国国际进口博览会意向成交金额达735.2亿美元.会期六天,平均每天达成意向成交金额多少亿美元?(精确到0.1亿美元)
解:平均每天达成意向成交金额为
735.2÷6≈122.53≈122.5(亿美元).
例3 “十一”期间,某商场准备对商品打8折促销.一种原价为348元的微波炉,打折后,如果精确到元,定价是多少?
解:这种微波炉打8折后的价格为
348278.4(元)
精确到元的定价为278元.
2.数4是4.3的近似值,其中4.3叫做真值,若一个数经四舍五入得到的近似数是12,则下列各数中不可能是12的真值的是( )
A. 12.38 B. 12.66 C. 11.99 D. 12.42
随堂练习
1.下列结论正确的是( )
A. 近似数4.230和4.23的精确度是一样的
B. 近似数89.0是精确到个位
C. 近似数0.00510与0.0510的精确度不一样
D. 近似数6万与近似数60 000的精确度相同
C
B
3.下列由四舍五入得到的近似数,各精确到哪一位?
(1)0.00407;(2)1.0;
(3)1.03万; (4)3.90×105.
解:(1)精确到0.00001(或十万分位);
(2)精确到0.1(或十分位);
(3)1.03万=10 300,故精确到百位;
(4)3.90×105=390 000,故精确到千位.
4.用四舍五入法,按括号中的要求对下列各数取近似数.
(1)2.009(精确到0.01); (2)46 854 000(精确到万位);
(3)4.762×107(精确到百万位); (4)13亿(精确到十万位).
解:(1)2.009≈2.01;
(2)46 854 000≈4.685×107;
(3)4.762×107≈4.8×107;
(4)13亿≈1.300 0×109 .
课堂总结
概念:
近似数是一个与实际数值很接近的数.
误差是近似值与它的准确值的差.
精确度表示近似数与准确数的接近程度.
近似数
应用:
判断近似数与准确数.
按照要求取近似数.
由近似数判断其精确度.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
