2.2 课时1 合并同类项 课件(共23张PPT) 2024-2025学年数学沪科版(2024)七年级上册
文档属性
| 名称 | 2.2 课时1 合并同类项 课件(共23张PPT) 2024-2025学年数学沪科版(2024)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 21:10:20 | ||
图片预览








文档简介
(共23张PPT)
课时1 合并同类项
2.2 整式加减
1. 在具体情境中感受合并同类项的必要性,理解合并同类项法则所依据的运算律; (重点)
2. 了解合并同类项的法则,能进行同类项的合并.(难点)
学习目标
垃圾分类不仅关系到城市的文明程度和城市形象,也是城市生态环境建设最基础工作.请观察,我们的生活垃圾是如何分类的?
情景导入
请同学们看以下图片,图片上有哪些物品可以归为一类?
水果
动物
服饰
生活中,我们常常把具有相同特征的事物归为一类,在多项式中,也可以把具有相同特征的项归为一类.
问题:你认为多项式中,哪些项可以归为一类?
探索 1:同类项的概念
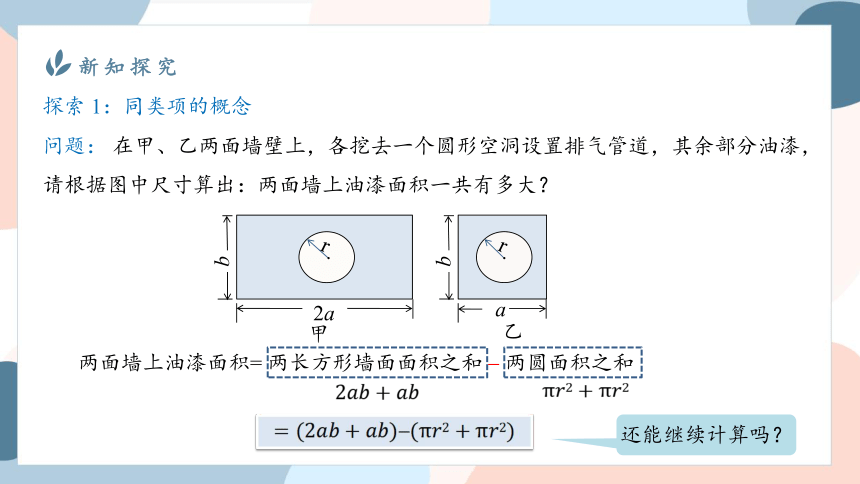
问题: 在甲、乙两面墙壁上,各挖去一个圆形空洞设置排气管道,其余部分油漆,请根据图中尺寸算出:两面墙上油漆面积一共有多大?
2a
b
r
·
甲
a
b
r
·
乙
两面墙上油漆面积= 两长方形墙面面积之和 两圆面积之和
还能继续计算吗?
新知探究
观察:中的两项和,中的两项和,它们有什么共同特征
项与都含字母和,并且的指数都是,的指数也都是;
项与都含字母,并且的指数都是.
像这样,所含字母相同,并且相同字母的指数也相同的项叫做同类项(like term).常数项与常数项是同类项.
1.所含字母相同
2.相同字母指数也相同
知识要点
归纳总结
例1
下列各组中的两个式子是同类项的是( )
A.2x2y与3xy2 B.10ax与6bx
C.a4与x4 D.π与3
导引:A中所含字母相同,但相同字母的指数不同;B中所含字母不同;C中所含字母不同;D中π是常数,与3是同类项.
D
典型例题
(3)与
(1)与
(2)与
(4) 与
先判断每一组是否是同类项,不是的,为前者配一个.
√
√
×
×
练一练
(1)同类项只与字母及其指数有关,与系数无关,与字母在单项式中的排列顺序无关;
(2)抓住“两个相同”:一是所含的字母要完全相同,二是相同字母的指数要相同,这两个条件缺一不可.
同类项的判别方法
(3)不要忘记几个单独的数也是同类项.
归纳总结
探索 2:合并同类项
在多项式中遇到同类项,可以运用加法交换律、加法结合律、分配律合并,如
新知探究
1.定义:把多项式中的同类项合并成一项,叫做合并同类项.
2.法则:同类项的系数相加,所得结果作为系数,字母和字母的指数不变.
现在你能计算下面的多项式了吗?
归纳总结
(1)
(2)
(3)
下列合并同类项对吗?不对的,说明理由.
(4)
(5)
(6)
×
√
×
×
×
√
练一练
例2
合并同类项.
解:
找
移
并
典型例题
例3
合并同类项.
解:
=
=
=
找
移
并
“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出,“—”“——” “ ” 等符号作标记,注意要包含该项的符号;
二移,利用加法的交换律,将不同类的同类项集中到不同的括号内;
三并,将同一括号内的同类项相加即可.
系数相加,字母及其指数不变
归纳总结
合并同类项:
(1);
(2)
解:(1)原式
(2)原式
先分组,再合并
练一练
习题1
A
下列式子正确的有( )
①2xy3-7y3x=-5x3y;②3x2y-2xy=1;
③a2+a2=a4;④3x+2y=5xy;
⑤4ab-4ab=ab;⑥-ab2- ab2=- ab2.
A.1个 B.2个 C.3个 D.4个
当堂检测
习题2
1.计算-3(x-2y)+4(x-2y)的结果是( )
A. x-2y B. x+2y C.-x-2y D.-x+2y
A
2. 若单项式 3x3y4n 与单项式 6x3ym 的和是 9x3y4n,则 m 与 n 的关系是( )
A. m=n B. m=4n
C. m=3n D.不能确定
B
习题3
1.合并同类项:
(1)
(2).
2.求值: ,其中
习题4
解:设土豆重a千克,篮子重b千克,若称篮子,应换0.5a千克苹果;若不称篮子,称苹果时也带篮子称,则换0.5a+0.5b-b=0.5a-0.5b千克的苹果.小明奶奶少得0.5b千克的苹果.所以摊主说的没道理.
一天,王村的小明奶奶提着一篮子土豆去换苹果,双方商定的结果是:1千克土豆换0.5千克苹果.当称完带篮子的土豆重量后,摊主对小明奶奶说:“别称篮子的重量了,称苹果时也带篮子称,这样既省事又互不吃亏.”你认为摊主的话有道理吗?请你用所学的有关数学知识加以解决.
合并同类项
同类项的概念
合并同类项的方法
“一加二不变”
两同
两无关
相同字母的指数相同
所含字母相同
与所含字母的顺序无关
与系数无关(不为0)
课堂总结
课时1 合并同类项
2.2 整式加减
1. 在具体情境中感受合并同类项的必要性,理解合并同类项法则所依据的运算律; (重点)
2. 了解合并同类项的法则,能进行同类项的合并.(难点)
学习目标
垃圾分类不仅关系到城市的文明程度和城市形象,也是城市生态环境建设最基础工作.请观察,我们的生活垃圾是如何分类的?
情景导入
请同学们看以下图片,图片上有哪些物品可以归为一类?
水果
动物
服饰
生活中,我们常常把具有相同特征的事物归为一类,在多项式中,也可以把具有相同特征的项归为一类.
问题:你认为多项式中,哪些项可以归为一类?
探索 1:同类项的概念
问题: 在甲、乙两面墙壁上,各挖去一个圆形空洞设置排气管道,其余部分油漆,请根据图中尺寸算出:两面墙上油漆面积一共有多大?
2a
b
r
·
甲
a
b
r
·
乙
两面墙上油漆面积= 两长方形墙面面积之和 两圆面积之和
还能继续计算吗?
新知探究
观察:中的两项和,中的两项和,它们有什么共同特征
项与都含字母和,并且的指数都是,的指数也都是;
项与都含字母,并且的指数都是.
像这样,所含字母相同,并且相同字母的指数也相同的项叫做同类项(like term).常数项与常数项是同类项.
1.所含字母相同
2.相同字母指数也相同
知识要点
归纳总结
例1
下列各组中的两个式子是同类项的是( )
A.2x2y与3xy2 B.10ax与6bx
C.a4与x4 D.π与3
导引:A中所含字母相同,但相同字母的指数不同;B中所含字母不同;C中所含字母不同;D中π是常数,与3是同类项.
D
典型例题
(3)与
(1)与
(2)与
(4) 与
先判断每一组是否是同类项,不是的,为前者配一个.
√
√
×
×
练一练
(1)同类项只与字母及其指数有关,与系数无关,与字母在单项式中的排列顺序无关;
(2)抓住“两个相同”:一是所含的字母要完全相同,二是相同字母的指数要相同,这两个条件缺一不可.
同类项的判别方法
(3)不要忘记几个单独的数也是同类项.
归纳总结
探索 2:合并同类项
在多项式中遇到同类项,可以运用加法交换律、加法结合律、分配律合并,如
新知探究
1.定义:把多项式中的同类项合并成一项,叫做合并同类项.
2.法则:同类项的系数相加,所得结果作为系数,字母和字母的指数不变.
现在你能计算下面的多项式了吗?
归纳总结
(1)
(2)
(3)
下列合并同类项对吗?不对的,说明理由.
(4)
(5)
(6)
×
√
×
×
×
√
练一练
例2
合并同类项.
解:
找
移
并
典型例题
例3
合并同类项.
解:
=
=
=
找
移
并
“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出,“—”“——” “ ” 等符号作标记,注意要包含该项的符号;
二移,利用加法的交换律,将不同类的同类项集中到不同的括号内;
三并,将同一括号内的同类项相加即可.
系数相加,字母及其指数不变
归纳总结
合并同类项:
(1);
(2)
解:(1)原式
(2)原式
先分组,再合并
练一练
习题1
A
下列式子正确的有( )
①2xy3-7y3x=-5x3y;②3x2y-2xy=1;
③a2+a2=a4;④3x+2y=5xy;
⑤4ab-4ab=ab;⑥-ab2- ab2=- ab2.
A.1个 B.2个 C.3个 D.4个
当堂检测
习题2
1.计算-3(x-2y)+4(x-2y)的结果是( )
A. x-2y B. x+2y C.-x-2y D.-x+2y
A
2. 若单项式 3x3y4n 与单项式 6x3ym 的和是 9x3y4n,则 m 与 n 的关系是( )
A. m=n B. m=4n
C. m=3n D.不能确定
B
习题3
1.合并同类项:
(1)
(2).
2.求值: ,其中
习题4
解:设土豆重a千克,篮子重b千克,若称篮子,应换0.5a千克苹果;若不称篮子,称苹果时也带篮子称,则换0.5a+0.5b-b=0.5a-0.5b千克的苹果.小明奶奶少得0.5b千克的苹果.所以摊主说的没道理.
一天,王村的小明奶奶提着一篮子土豆去换苹果,双方商定的结果是:1千克土豆换0.5千克苹果.当称完带篮子的土豆重量后,摊主对小明奶奶说:“别称篮子的重量了,称苹果时也带篮子称,这样既省事又互不吃亏.”你认为摊主的话有道理吗?请你用所学的有关数学知识加以解决.
合并同类项
同类项的概念
合并同类项的方法
“一加二不变”
两同
两无关
相同字母的指数相同
所含字母相同
与所含字母的顺序无关
与系数无关(不为0)
课堂总结
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
