2024-2025学年苏科版九年级上册数学期中测试卷(第一章-第二章)(含答案)
文档属性
| 名称 | 2024-2025学年苏科版九年级上册数学期中测试卷(第一章-第二章)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 393.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 19:32:40 | ||
图片预览



文档简介
2024-2025学年苏科版九年级上册数学期中测试卷(第一章-第二章)
考试时间:120分钟 满分:100分
一、单选题(共10题;共30分)
1.(3分)如图,点A,B,C在⊙O上,若,则的度数为( )
A. B. C. D.
2.(3分)已知m,n是方程的两实数根,则的值为( )
A.-1 B. C. D.1
3.(3分)取一张长与宽之比为的矩形纸板,剪去四个边长为的小正方形(如图),并用它做一个无盖的矩形形状的包装盒.要使包装盒的容积为(纸板的厚度略去不计),问这张矩形纸板的长与宽分别为多少厘米?若设这张矩形纸板的长为厘米,则由题意可列出的方程是( )
A. B.
C. D.
4.(3分)如图,在△ABC中,AB=AC,点D在AC边上,过△ABD的内心I作IE⊥BD于点E.若BD=10,CD=4,则BE的长为( )
A.6 B.7 C.8 D.9
5.(3分)生活中常见的轮子都是圆形,有一种特殊的莱洛三角形,是由三段相等的圆弧构成,虽然不是圆但是做成滚轮同样不会颠簸,其原理为每个顶点到所对圆弧的距离都为等边三角形的边长,已知的中心O到三个顶点的距离均为,则这个莱落三角形的周长等于( )
A. B. C. D.
6.(3分)如图所示,AB为⊙O的直径,点C在⊙O上,且OC⊥AB,过点C的弦CD与线段OB相交于点E,满足∠AEC=65°,连接AD,则∠BAD等于( )
A.20° B.25° C.30° D.32.5°
7.(3分)某制药厂生产的某种针剂,每支成本3元,由于连续两次降低成本,现在的成本是2.43元,则平均每次降低成本的百分率是( )
A. B. C. D.
8.(3分)如图,在菱形ABCD中,点P是BC边上一动点,连结AP,AP的垂直平分线交BD于点G,交 AP于点E,在P点由B点到C点的运动过程中,∠APG的大小变化情况是( )
A.变大 B.先变大后变小
C.先变小后变大 D.不变
9.(3分)如图,已知正方形的边长为4,动点P从点A出发在边上运动,同时动点Q从点B出发以同样的速度在边上运动.分别连接与相交于点E,连接,则线段的最小值为( )
A. B. C. D.
10.(3分)从a,b,c三个数中任意取两个数相加再减去第三个数,根据不同的选择得到三个结果,,,称为一次操作.下列说法:
①若,,,则,,三个数中最大的数是4;
②若,,,且,,中最小值为,则;
③给定a,b,c三个数,将第一次操作的三个结果,,按上述方法再进行一次操作,得到三个结果,,,以此类推,第n次操作的结果是,,,则的值为定值.
其中正确的个数是( )
A.3 B.2 C.1 D.0
二、填空题(共8题;共27分)
11.(3分)如果a、b是一元二次方程x2﹣x﹣3=0的两个实数根,则多项式3b2+ab+3a的值为 .
12.(3分)我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深寸,锯道长尺(1尺寸).问这根圆形木材的直径是 寸.
13.(6分)如图所示的网格由边长均为1的小正方形组成,点A、B、C、D、E、F在小正方形的顶点上,则外接圆的圆心是点 ,弧的长是 .
14.(3分)已知扇形的圆心角是,半径是,则扇形的弧长为 cm.
15.(3分)已知圆锥的底面圆的半径是2.5,母线长是6,其侧面展开图的面积 .
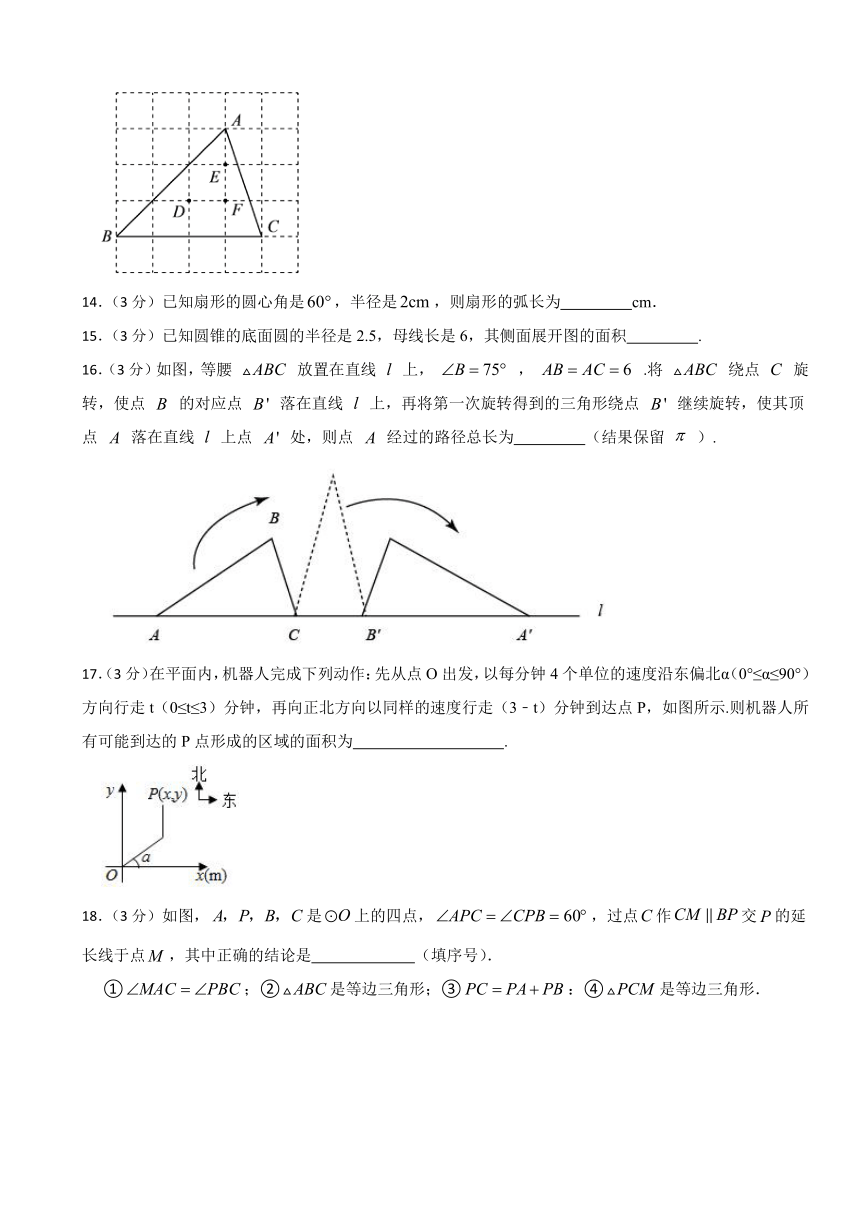
16.(3分)如图,等腰 放置在直线 上, , .将 绕点 旋转,使点 的对应点 落在直线 上,再将第一次旋转得到的三角形绕点 继续旋转,使其顶点 落在直线 上点 处,则点 经过的路径总长为 (结果保留 ).
17.(3分)在平面内,机器人完成下列动作:先从点O出发,以每分钟4个单位的速度沿东偏北α(0°≤α≤90°)方向行走t(0≤t≤3)分钟,再向正北方向以同样的速度行走(3﹣t)分钟到达点P,如图所示.则机器人所有可能到达的P点形成的区域的面积为 .
18.(3分)如图,是上的四点,,过点作交的延长线于点,其中正确的结论是 (填序号).
①;②是等边三角形;③:④是等边三角形.
三、解答题(共6题;共43分)
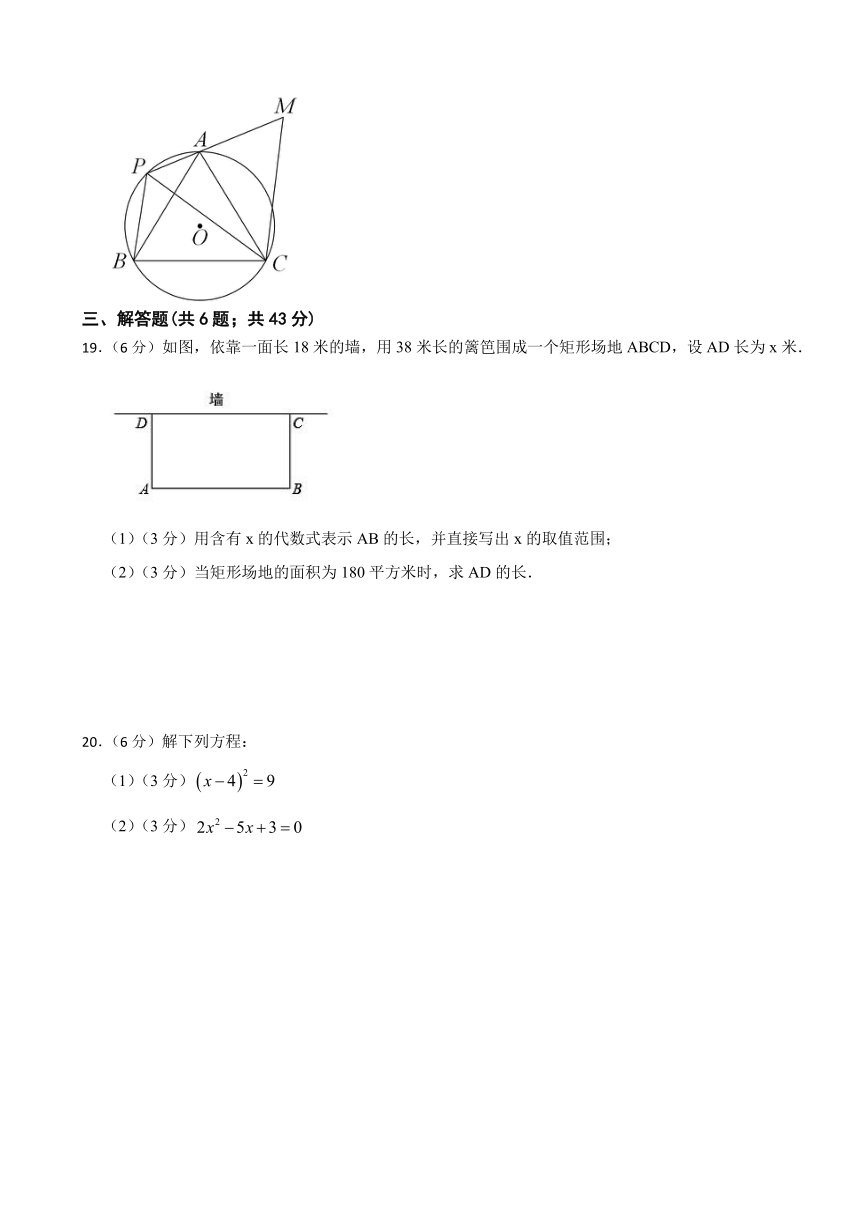
19.(6分)如图,依靠一面长18米的墙,用38米长的篱笆围成一个矩形场地ABCD,设AD长为x米.
(1)(3分)用含有x的代数式表示AB的长,并直接写出x的取值范围;
(2)(3分)当矩形场地的面积为180平方米时,求AD的长.
20.(6分)解下列方程:
(1)(3分)
(2)(3分)
21.(7分)如图所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC于E.
(1)(3分)求证:AB=AC;
(2)(4分)求证:DE为⊙O的切线.
22.(7分)已知关于x的一元二次方程.
(1)(3分)若方程有实数根,求实数的取值范围;
(2)(4分)若方程两实数根分别为和,且满足,求实数的值.
23.(8分)如图,小华要为一个长6分米,宽4分米的长方形防疫科普电子小报四周添加一个边框,要求边框的上下左右宽度相等,且边框面积与电子小报内容所占面积相等.求小华添加的边框的宽度.
24.(9分)小亮创办了一个微店商铺,营销一款小型护眼台灯,成本是元台厂商建议,台灯的标价应不低于元台,且不高于元台.
(1)(4分)小亮根据日常销售的数据发现,当销售价格为元台时,每天能售出台;若台灯的价格每上涨元,日销量会下降台求日销售量台与元台之间的函数关系式;
(2)(5分)“”促销日之前的销售数据显示,最高日销售利润为元“”当天,小亮为提高店铺知名度,采用如下促销方式:台灯按元台标价,并打折销售;当天销售量在台的基础上增加了倍,日销售利润上升为“”促销日之前的最高日销售利润的倍,求的值.
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】A
7.【答案】A
8.【答案】D
9.【答案】D
10.【答案】C
11.【答案】
12.【答案】26
13.【答案】D;
14.【答案】
15.【答案】15π
16.【答案】7π
17.【答案】(36π﹣72)m2
18.【答案】
19.【答案】(1)
(2)10米
20.【答案】(1),
(2),
21.【答案】(1)证明:连接AD;
∵AB是⊙O的直径,
∴∠ADB=90°.
又∵DC=BD,
∴AD是BC的中垂线.
∴AB=AC.
(2)证明:连接OD;
∵OA=OB,CD=BD,
∴OD∥AC.
∴∠ODE=∠CED.
又∵DE⊥AC,
∴∠CED=90°.
∴∠ODE=90°,即OD⊥DE.
∴DE是⊙O的切线.
22.【答案】(1)解:∵有实数根,
∴,
即:,
∴.
(2)解:根据题意可得:,,
当,则,
即,
,
解得:,,
∵,
∴不符合题意,舍去,
∴.
23.【答案】解:设小华添加的边框的宽度应是x分米,
依题意,得:(6+2x)(4+2x)﹣6×4=6×4,
整理,得:x2+5x﹣6=0,
解得:x1=1,x2=﹣6(不合题意,舍去).
答:小华添加的边框的宽度应是1分米.
24.【答案】(1)解:根据题意可得:日销售量盏与时间天之间的函数关系式为:
(2)解:根据题意列方程:,
整理得:.
解得或舍去.
考试时间:120分钟 满分:100分
一、单选题(共10题;共30分)
1.(3分)如图,点A,B,C在⊙O上,若,则的度数为( )
A. B. C. D.
2.(3分)已知m,n是方程的两实数根,则的值为( )
A.-1 B. C. D.1
3.(3分)取一张长与宽之比为的矩形纸板,剪去四个边长为的小正方形(如图),并用它做一个无盖的矩形形状的包装盒.要使包装盒的容积为(纸板的厚度略去不计),问这张矩形纸板的长与宽分别为多少厘米?若设这张矩形纸板的长为厘米,则由题意可列出的方程是( )
A. B.
C. D.
4.(3分)如图,在△ABC中,AB=AC,点D在AC边上,过△ABD的内心I作IE⊥BD于点E.若BD=10,CD=4,则BE的长为( )
A.6 B.7 C.8 D.9
5.(3分)生活中常见的轮子都是圆形,有一种特殊的莱洛三角形,是由三段相等的圆弧构成,虽然不是圆但是做成滚轮同样不会颠簸,其原理为每个顶点到所对圆弧的距离都为等边三角形的边长,已知的中心O到三个顶点的距离均为,则这个莱落三角形的周长等于( )
A. B. C. D.
6.(3分)如图所示,AB为⊙O的直径,点C在⊙O上,且OC⊥AB,过点C的弦CD与线段OB相交于点E,满足∠AEC=65°,连接AD,则∠BAD等于( )
A.20° B.25° C.30° D.32.5°
7.(3分)某制药厂生产的某种针剂,每支成本3元,由于连续两次降低成本,现在的成本是2.43元,则平均每次降低成本的百分率是( )
A. B. C. D.
8.(3分)如图,在菱形ABCD中,点P是BC边上一动点,连结AP,AP的垂直平分线交BD于点G,交 AP于点E,在P点由B点到C点的运动过程中,∠APG的大小变化情况是( )
A.变大 B.先变大后变小
C.先变小后变大 D.不变
9.(3分)如图,已知正方形的边长为4,动点P从点A出发在边上运动,同时动点Q从点B出发以同样的速度在边上运动.分别连接与相交于点E,连接,则线段的最小值为( )
A. B. C. D.
10.(3分)从a,b,c三个数中任意取两个数相加再减去第三个数,根据不同的选择得到三个结果,,,称为一次操作.下列说法:
①若,,,则,,三个数中最大的数是4;
②若,,,且,,中最小值为,则;
③给定a,b,c三个数,将第一次操作的三个结果,,按上述方法再进行一次操作,得到三个结果,,,以此类推,第n次操作的结果是,,,则的值为定值.
其中正确的个数是( )
A.3 B.2 C.1 D.0
二、填空题(共8题;共27分)
11.(3分)如果a、b是一元二次方程x2﹣x﹣3=0的两个实数根,则多项式3b2+ab+3a的值为 .
12.(3分)我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”意思是:今有一圆柱形木材,埋在墙壁中,不知其大小.用锯去锯这木材,锯口深寸,锯道长尺(1尺寸).问这根圆形木材的直径是 寸.
13.(6分)如图所示的网格由边长均为1的小正方形组成,点A、B、C、D、E、F在小正方形的顶点上,则外接圆的圆心是点 ,弧的长是 .
14.(3分)已知扇形的圆心角是,半径是,则扇形的弧长为 cm.
15.(3分)已知圆锥的底面圆的半径是2.5,母线长是6,其侧面展开图的面积 .
16.(3分)如图,等腰 放置在直线 上, , .将 绕点 旋转,使点 的对应点 落在直线 上,再将第一次旋转得到的三角形绕点 继续旋转,使其顶点 落在直线 上点 处,则点 经过的路径总长为 (结果保留 ).
17.(3分)在平面内,机器人完成下列动作:先从点O出发,以每分钟4个单位的速度沿东偏北α(0°≤α≤90°)方向行走t(0≤t≤3)分钟,再向正北方向以同样的速度行走(3﹣t)分钟到达点P,如图所示.则机器人所有可能到达的P点形成的区域的面积为 .
18.(3分)如图,是上的四点,,过点作交的延长线于点,其中正确的结论是 (填序号).
①;②是等边三角形;③:④是等边三角形.
三、解答题(共6题;共43分)
19.(6分)如图,依靠一面长18米的墙,用38米长的篱笆围成一个矩形场地ABCD,设AD长为x米.
(1)(3分)用含有x的代数式表示AB的长,并直接写出x的取值范围;
(2)(3分)当矩形场地的面积为180平方米时,求AD的长.
20.(6分)解下列方程:
(1)(3分)
(2)(3分)
21.(7分)如图所示,AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使DC=BD,连接AC,过点D作DE⊥AC于E.
(1)(3分)求证:AB=AC;
(2)(4分)求证:DE为⊙O的切线.
22.(7分)已知关于x的一元二次方程.
(1)(3分)若方程有实数根,求实数的取值范围;
(2)(4分)若方程两实数根分别为和,且满足,求实数的值.
23.(8分)如图,小华要为一个长6分米,宽4分米的长方形防疫科普电子小报四周添加一个边框,要求边框的上下左右宽度相等,且边框面积与电子小报内容所占面积相等.求小华添加的边框的宽度.
24.(9分)小亮创办了一个微店商铺,营销一款小型护眼台灯,成本是元台厂商建议,台灯的标价应不低于元台,且不高于元台.
(1)(4分)小亮根据日常销售的数据发现,当销售价格为元台时,每天能售出台;若台灯的价格每上涨元,日销量会下降台求日销售量台与元台之间的函数关系式;
(2)(5分)“”促销日之前的销售数据显示,最高日销售利润为元“”当天,小亮为提高店铺知名度,采用如下促销方式:台灯按元台标价,并打折销售;当天销售量在台的基础上增加了倍,日销售利润上升为“”促销日之前的最高日销售利润的倍,求的值.
答案解析部分
1.【答案】C
2.【答案】A
3.【答案】D
4.【答案】B
5.【答案】B
6.【答案】A
7.【答案】A
8.【答案】D
9.【答案】D
10.【答案】C
11.【答案】
12.【答案】26
13.【答案】D;
14.【答案】
15.【答案】15π
16.【答案】7π
17.【答案】(36π﹣72)m2
18.【答案】
19.【答案】(1)
(2)10米
20.【答案】(1),
(2),
21.【答案】(1)证明:连接AD;
∵AB是⊙O的直径,
∴∠ADB=90°.
又∵DC=BD,
∴AD是BC的中垂线.
∴AB=AC.
(2)证明:连接OD;
∵OA=OB,CD=BD,
∴OD∥AC.
∴∠ODE=∠CED.
又∵DE⊥AC,
∴∠CED=90°.
∴∠ODE=90°,即OD⊥DE.
∴DE是⊙O的切线.
22.【答案】(1)解:∵有实数根,
∴,
即:,
∴.
(2)解:根据题意可得:,,
当,则,
即,
,
解得:,,
∵,
∴不符合题意,舍去,
∴.
23.【答案】解:设小华添加的边框的宽度应是x分米,
依题意,得:(6+2x)(4+2x)﹣6×4=6×4,
整理,得:x2+5x﹣6=0,
解得:x1=1,x2=﹣6(不合题意,舍去).
答:小华添加的边框的宽度应是1分米.
24.【答案】(1)解:根据题意可得:日销售量盏与时间天之间的函数关系式为:
(2)解:根据题意列方程:,
整理得:.
解得或舍去.
同课章节目录
