2016届(沪科)九年级数学下册课件第24章圆小结与评价(共30张PPT)
文档属性
| 名称 | 2016届(沪科)九年级数学下册课件第24章圆小结与评价(共30张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 456.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-02-28 15:30:41 | ||
图片预览



文档简介
课件30张PPT。小结与评价义务教育教科书(沪科)九年级数学下册
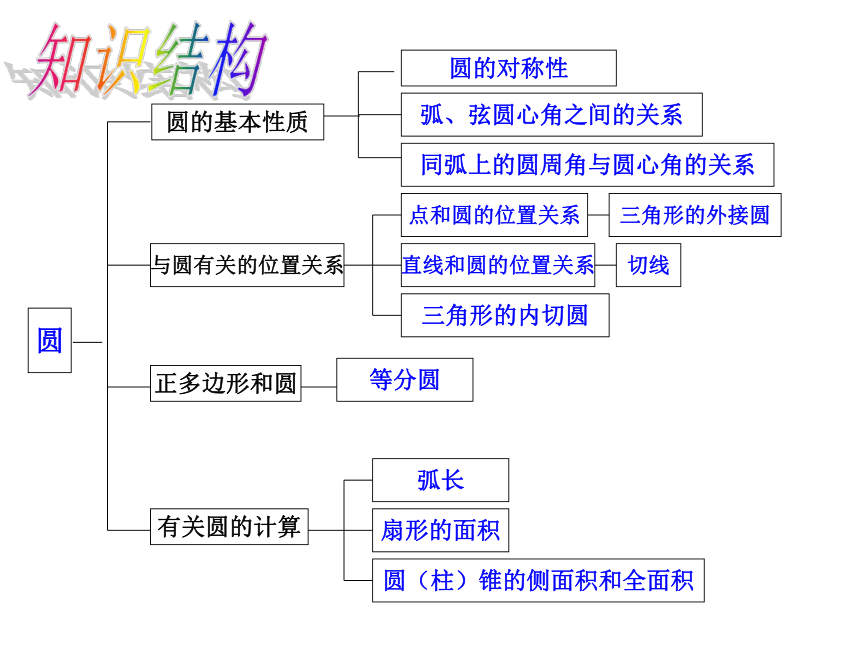
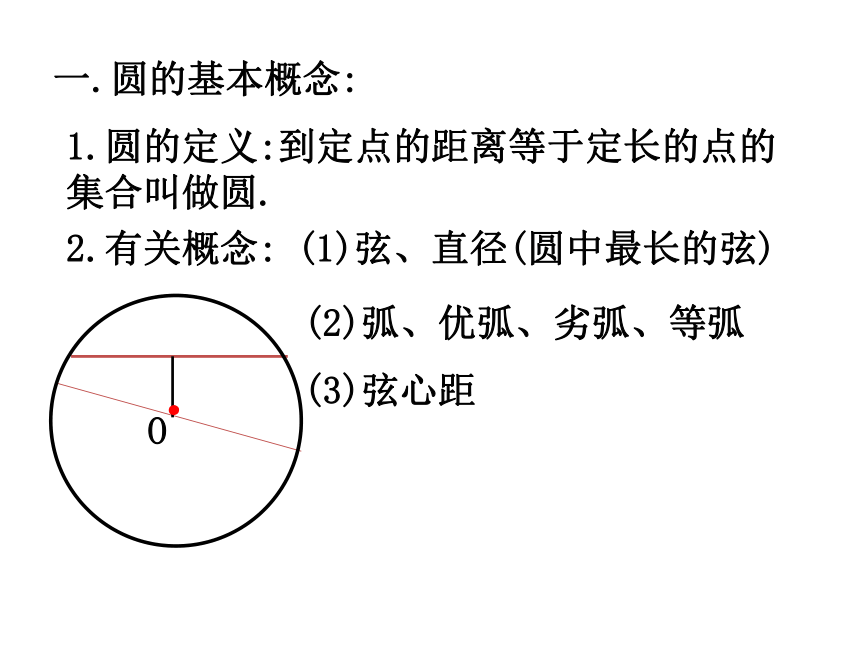
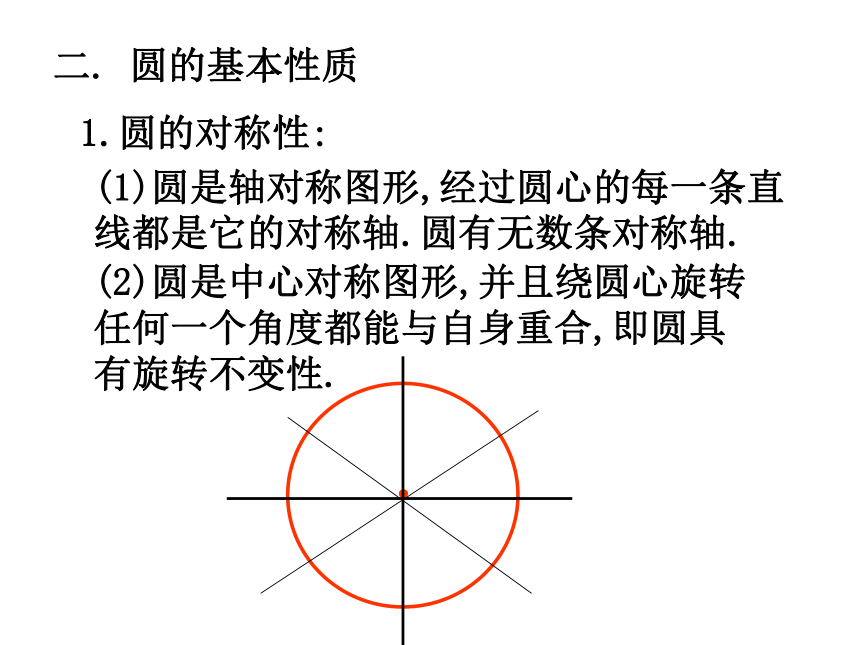
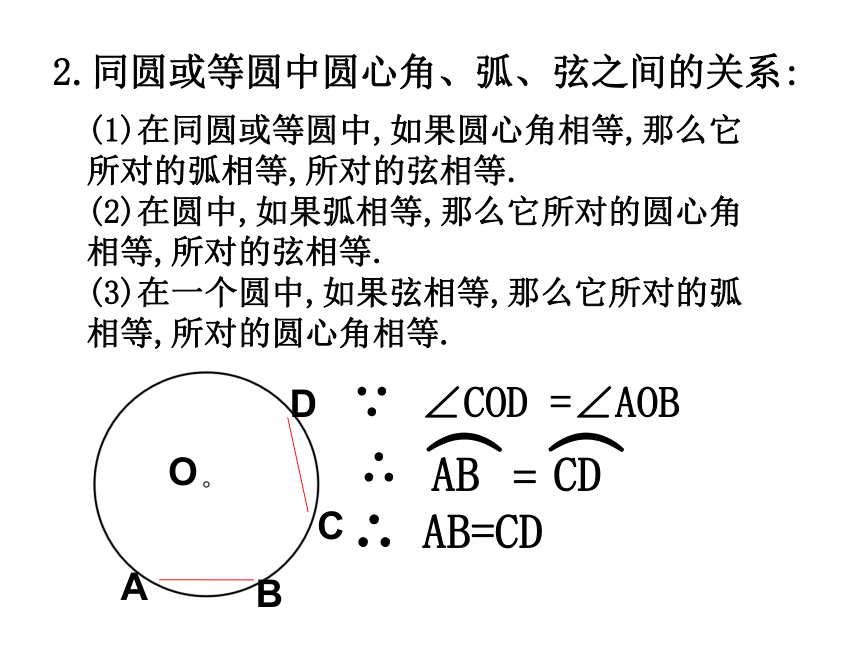
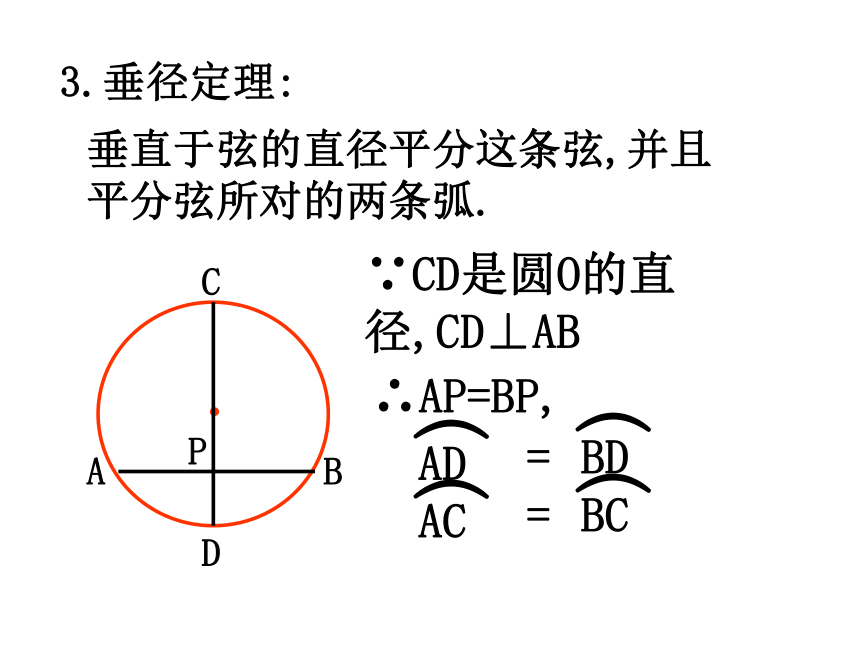
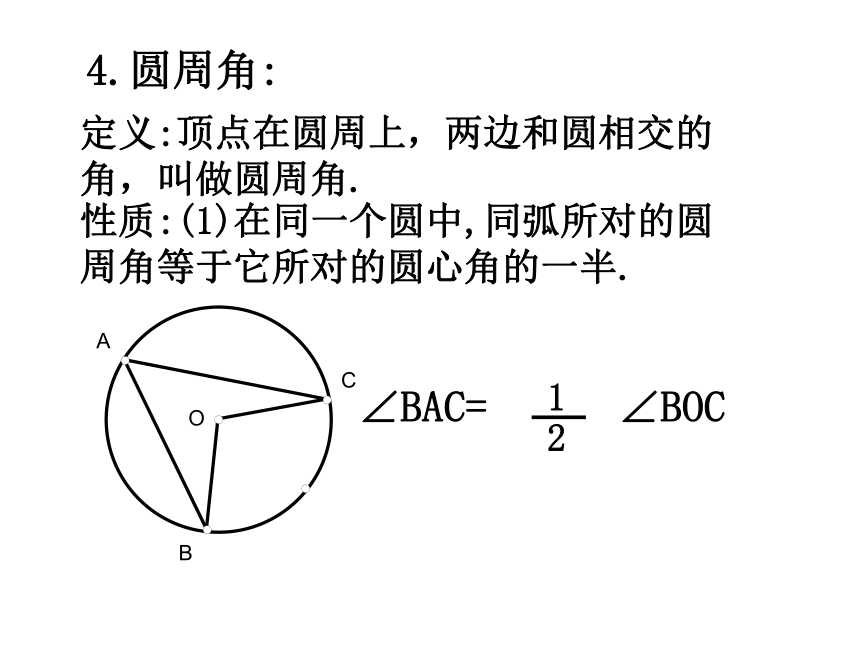
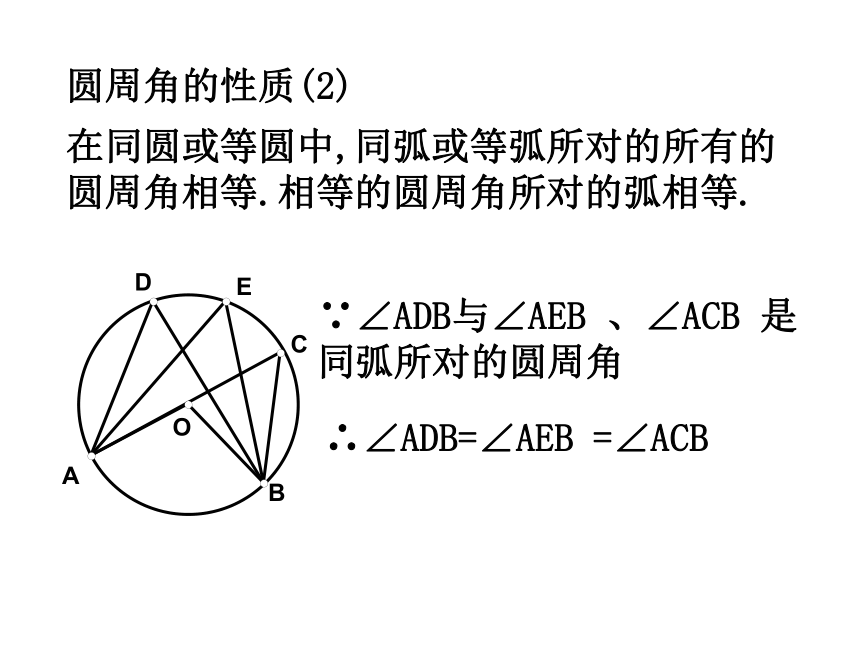
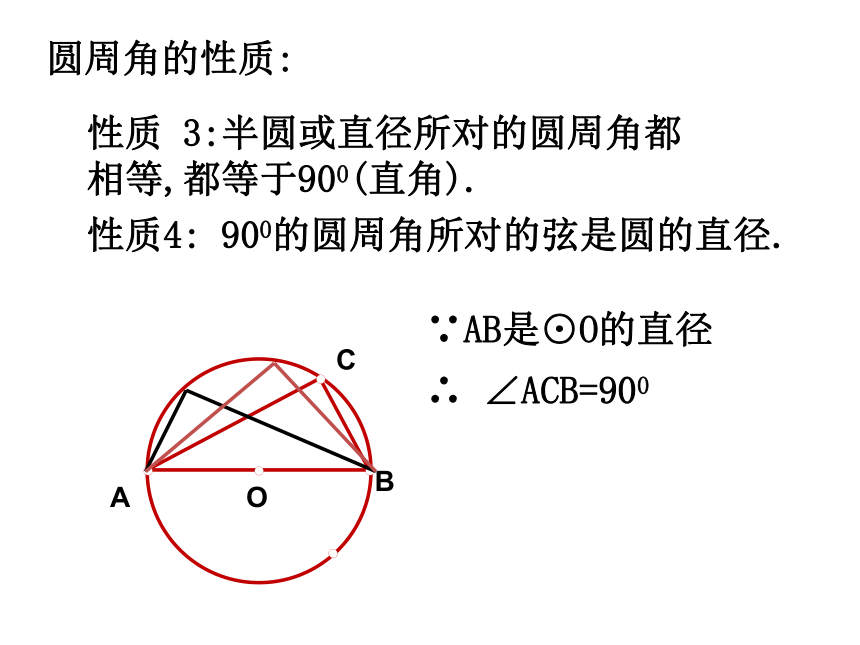
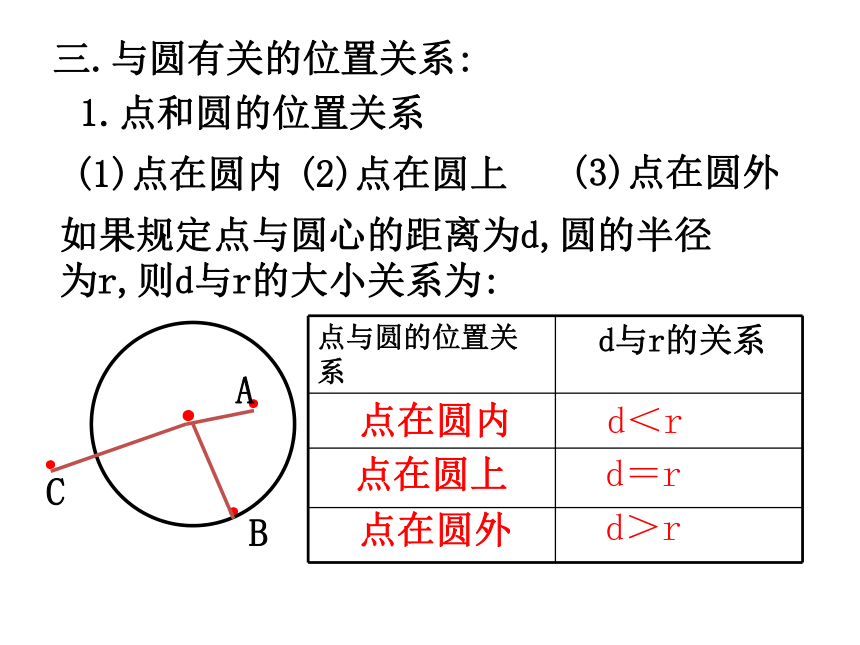
第24章 圆 圆的基本性质圆圆的对称性弧、弦圆心角之间的关系同弧上的圆周角与圆心角的关系与圆有关的位置关系正多边形和圆有关圆的计算点和圆的位置关系切线直线和圆的位置关系三角形的外接圆等分圆三角形的内切圆弧长扇形的面积圆(柱)锥的侧面积和全面积知识结构第1部分 圆的基本性质第2部分 与圆有关的位置关系第3部分 正多边形和圆第4部分 弧长和面积的计算第5部分 有关作图知识梳理一.圆的基本概念:1.圆的定义:到定点的距离等于定长的点的集合叫做圆.2.有关概念:(1)弦、直径(圆中最长的弦)(2)弧、优弧、劣弧、等弧(3)弦心距二. 圆的基本性质1.圆的对称性:(1)圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.圆有无数条对称轴.(2)圆是中心对称图形,并且绕圆心旋转任何一个角度都能与自身重合,即圆具有旋转不变性.2.同圆或等圆中圆心角、弧、弦之间的关系:(1)在同圆或等圆中,如果圆心角相等,那么它所对的弧相等,所对的弦相等.(2)在圆中,如果弧相等,那么它所对的圆心角相等,所对的弦相等.(3)在一个圆中,如果弦相等,那么它所对的弧相等,所对的圆心角相等.∵ ∠COD =∠AOB∴∴ AB=CD3.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.∵CD是圆O的直径,CD⊥AB∴AP=BP, 对于一个圆中的弦长a、圆心到弦的距离d、圆半径r、弓形高h,这四个量中,只要已知其中任意两个量,就可以求出另外两个量,如图有:⑴d + h = r⑵垂径定理的应用 4.圆周角:定义:顶点在圆周上,两边和圆相交的角,叫做圆周角.性质:(1)在同一个圆中,同弧所对的圆周角等于它所对的圆心角的一半.在同圆或等圆中,同弧或等弧所对的所有的圆周角相等.相等的圆周角所对的弧相等.圆周角的性质(2)∵∠ADB与∠AEB 、∠ACB 是同弧所对的圆周角∴∠ADB=∠AEB =∠ACB性质 3:半圆或直径所对的圆周角都相等,都等于900(直角).性质4: 900的圆周角所对的弦是圆的直径.∵AB是⊙O的直径∴ ∠ACB=900圆周角的性质:(2)点在圆上(3)点在圆外(1)点在圆内...如果规定点与圆心的距离为d,圆的半径为r,则d与r的大小关系为:点在圆内点在圆上点在圆外d<rd=rd>r三.与圆有关的位置关系:2.直线和圆的位置关系:(1) 相离:(2) 相切:(3) 相交:一条直线与一个圆没有公共点,叫做直线与这个圆相离.一条直线与一个圆只有一个公共点,叫做直线与这个圆相切.一条直线与一个圆有两个公共点,叫做直线与这个圆相交.(1)当直线与圆相离时d>r;(2)当直线与圆相切时d =r;(3)当直线与圆相交时d<r.3.直线与圆位置关系的识别:∟dr设圆的半径为r,圆心到直线的距离为d,则:1.与圆有一个公共点的直线。2.圆心到直线的距离等于圆的半径的直线是圆的切线。3.经过半径的外端且垂直于这条半径的直线是圆的切线。A∟l∵OA是半径,OA⊥ l∴直线l是⊙O的切线.4.切线:切线的性质:(1)圆的切线垂直于经过切点的半径.(2)经过圆心垂直于切线的直线必经过切点.(3)经过切点垂直于切线的直线必经过圆心..A∟l∴ OA⊥ l∵直线l是⊙O的切线,切点为A切线长定理: 从圆外一点引圆的两条切线,它们的切线长相等;这点与圆心的连线平分这两条切线的夹角。BAPO∵PA、PB为⊙O的切线∴PA=PB,∠APO= ∠BPO不在同一直线上的三点确定一个圆.三角形的外接圆与内切圆:三角形的外心就是三角形各边垂直平分线的交点.三角形的内心就是三角形各角平分线的交点.等边三角形的外心与内心重合.特别的:内切圆半径与外接圆半径的比是1:2.OD四.正多边形与圆:2.半径:正多边形外接圆的半径叫做这个正多边形的半径.1.中心:一个正多边形外接圆的圆心叫做这个正多边形的中心.3.中心角:正多边形每一边所对的外接圆的圆心角叫做这个正多边形的中心角.4.边心距:中心到正多边形一边的距离叫做这个正多边形的边心距.O1.圆的周长和面积公式2.弧长的计算公式3.扇形的面积公式或圆中的有关计算:周长C=2πr面积s=πr24.圆柱的展开图:rhS侧 =2πr hS全=2πr h+2 π r25.圆锥的展开图:底面侧面aahrS侧 =πr aS全=πr a+ π r2常见的基本图形及结论:∟1.如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D,则:AC=BD若大圆的弦切小圆于C,则OAC=BC两圆之间的环形面积.S= πAB21.如图,以等腰△ABC的腰AB为直径作⊙O交底边BC于点D,则:OCBAD点D是BC的中点.经典例题O...PBADC2.如图,已知PA、PB切圆O于点A,B,过弧AB上任一点E作圆O的切线,交PA,PB于点C,D,则:(1) △PCD的周长=2PA(2) ∠COD= 900- ∠APBEDFEDFE3.如图, △ABC各边分别切圆O于点D、E、F.(1) ∠DEF= 900- ∠A(3) S △ABC= (a+b+c)r(2) ∠BOC= 900+ ∠A4.如图,AB是圆O的直径,AD,BC,DC均为切线,则:(1)DC=AD+BC(2) ∠DOC=900五.与圆有关的辅助线的作法:辅助线, 莫乱添, 规律方法记心间;圆半径, 不起眼, 角的计算常要连,构成等腰解疑难;切点和圆心, 连结要领先; 遇到直径想直角, 灵活应用才方便。
弦与弦心距, 亲密紧相连;
如图, ⊙O的直径AB=12,以OA为直径的⊙O1交大圆的弦AC于D,过D点作小圆的切线交OC于点E,交AB于F.EO1ODCBAF(2)猜想DF与OC的位置关系,并说明理由.(1)说明D是AC的中点.(3)若DF=4,求OF的长.经典例题
第24章 圆 圆的基本性质圆圆的对称性弧、弦圆心角之间的关系同弧上的圆周角与圆心角的关系与圆有关的位置关系正多边形和圆有关圆的计算点和圆的位置关系切线直线和圆的位置关系三角形的外接圆等分圆三角形的内切圆弧长扇形的面积圆(柱)锥的侧面积和全面积知识结构第1部分 圆的基本性质第2部分 与圆有关的位置关系第3部分 正多边形和圆第4部分 弧长和面积的计算第5部分 有关作图知识梳理一.圆的基本概念:1.圆的定义:到定点的距离等于定长的点的集合叫做圆.2.有关概念:(1)弦、直径(圆中最长的弦)(2)弧、优弧、劣弧、等弧(3)弦心距二. 圆的基本性质1.圆的对称性:(1)圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.圆有无数条对称轴.(2)圆是中心对称图形,并且绕圆心旋转任何一个角度都能与自身重合,即圆具有旋转不变性.2.同圆或等圆中圆心角、弧、弦之间的关系:(1)在同圆或等圆中,如果圆心角相等,那么它所对的弧相等,所对的弦相等.(2)在圆中,如果弧相等,那么它所对的圆心角相等,所对的弦相等.(3)在一个圆中,如果弦相等,那么它所对的弧相等,所对的圆心角相等.∵ ∠COD =∠AOB∴∴ AB=CD3.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.∵CD是圆O的直径,CD⊥AB∴AP=BP, 对于一个圆中的弦长a、圆心到弦的距离d、圆半径r、弓形高h,这四个量中,只要已知其中任意两个量,就可以求出另外两个量,如图有:⑴d + h = r⑵垂径定理的应用 4.圆周角:定义:顶点在圆周上,两边和圆相交的角,叫做圆周角.性质:(1)在同一个圆中,同弧所对的圆周角等于它所对的圆心角的一半.在同圆或等圆中,同弧或等弧所对的所有的圆周角相等.相等的圆周角所对的弧相等.圆周角的性质(2)∵∠ADB与∠AEB 、∠ACB 是同弧所对的圆周角∴∠ADB=∠AEB =∠ACB性质 3:半圆或直径所对的圆周角都相等,都等于900(直角).性质4: 900的圆周角所对的弦是圆的直径.∵AB是⊙O的直径∴ ∠ACB=900圆周角的性质:(2)点在圆上(3)点在圆外(1)点在圆内...如果规定点与圆心的距离为d,圆的半径为r,则d与r的大小关系为:点在圆内点在圆上点在圆外d<rd=rd>r三.与圆有关的位置关系:2.直线和圆的位置关系:(1) 相离:(2) 相切:(3) 相交:一条直线与一个圆没有公共点,叫做直线与这个圆相离.一条直线与一个圆只有一个公共点,叫做直线与这个圆相切.一条直线与一个圆有两个公共点,叫做直线与这个圆相交.(1)当直线与圆相离时d>r;(2)当直线与圆相切时d =r;(3)当直线与圆相交时d<r.3.直线与圆位置关系的识别:∟dr设圆的半径为r,圆心到直线的距离为d,则:1.与圆有一个公共点的直线。2.圆心到直线的距离等于圆的半径的直线是圆的切线。3.经过半径的外端且垂直于这条半径的直线是圆的切线。A∟l∵OA是半径,OA⊥ l∴直线l是⊙O的切线.4.切线:切线的性质:(1)圆的切线垂直于经过切点的半径.(2)经过圆心垂直于切线的直线必经过切点.(3)经过切点垂直于切线的直线必经过圆心..A∟l∴ OA⊥ l∵直线l是⊙O的切线,切点为A切线长定理: 从圆外一点引圆的两条切线,它们的切线长相等;这点与圆心的连线平分这两条切线的夹角。BAPO∵PA、PB为⊙O的切线∴PA=PB,∠APO= ∠BPO不在同一直线上的三点确定一个圆.三角形的外接圆与内切圆:三角形的外心就是三角形各边垂直平分线的交点.三角形的内心就是三角形各角平分线的交点.等边三角形的外心与内心重合.特别的:内切圆半径与外接圆半径的比是1:2.OD四.正多边形与圆:2.半径:正多边形外接圆的半径叫做这个正多边形的半径.1.中心:一个正多边形外接圆的圆心叫做这个正多边形的中心.3.中心角:正多边形每一边所对的外接圆的圆心角叫做这个正多边形的中心角.4.边心距:中心到正多边形一边的距离叫做这个正多边形的边心距.O1.圆的周长和面积公式2.弧长的计算公式3.扇形的面积公式或圆中的有关计算:周长C=2πr面积s=πr24.圆柱的展开图:rhS侧 =2πr hS全=2πr h+2 π r25.圆锥的展开图:底面侧面aahrS侧 =πr aS全=πr a+ π r2常见的基本图形及结论:∟1.如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C、D,则:AC=BD若大圆的弦切小圆于C,则OAC=BC两圆之间的环形面积.S= πAB21.如图,以等腰△ABC的腰AB为直径作⊙O交底边BC于点D,则:OCBAD点D是BC的中点.经典例题O...PBADC2.如图,已知PA、PB切圆O于点A,B,过弧AB上任一点E作圆O的切线,交PA,PB于点C,D,则:(1) △PCD的周长=2PA(2) ∠COD= 900- ∠APBEDFEDFE3.如图, △ABC各边分别切圆O于点D、E、F.(1) ∠DEF= 900- ∠A(3) S △ABC= (a+b+c)r(2) ∠BOC= 900+ ∠A4.如图,AB是圆O的直径,AD,BC,DC均为切线,则:(1)DC=AD+BC(2) ∠DOC=900五.与圆有关的辅助线的作法:辅助线, 莫乱添, 规律方法记心间;圆半径, 不起眼, 角的计算常要连,构成等腰解疑难;切点和圆心, 连结要领先; 遇到直径想直角, 灵活应用才方便。
弦与弦心距, 亲密紧相连;
如图, ⊙O的直径AB=12,以OA为直径的⊙O1交大圆的弦AC于D,过D点作小圆的切线交OC于点E,交AB于F.EO1ODCBAF(2)猜想DF与OC的位置关系,并说明理由.(1)说明D是AC的中点.(3)若DF=4,求OF的长.经典例题
