第十三章 轴对称 单元练习(含答案) 2024-2025学年数学人教版八年级上册
文档属性
| 名称 | 第十三章 轴对称 单元练习(含答案) 2024-2025学年数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 488.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-21 09:53:50 | ||
图片预览


文档简介
第十三章轴对称
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列“绿色食品、响应环保、可回收物、节水”四个标志图案中,属于轴对称图形的是( )
A. B. C. D.
2.等腰三角形的一个内角的度数是,则其底角的度数是( )
A. B. C. D. 或
3.如图,在中,,,与关于直线EF对称,,连接,则的度数是 ( )
A. B. C. D.
4.如图,直线,点A在直线上,点B在直线上,,,,则的度数是 ( )
A. B. C. D.
5.如图,O为三边垂直平分线的交点,且,则的度数为 ( )
A. B. C. D.
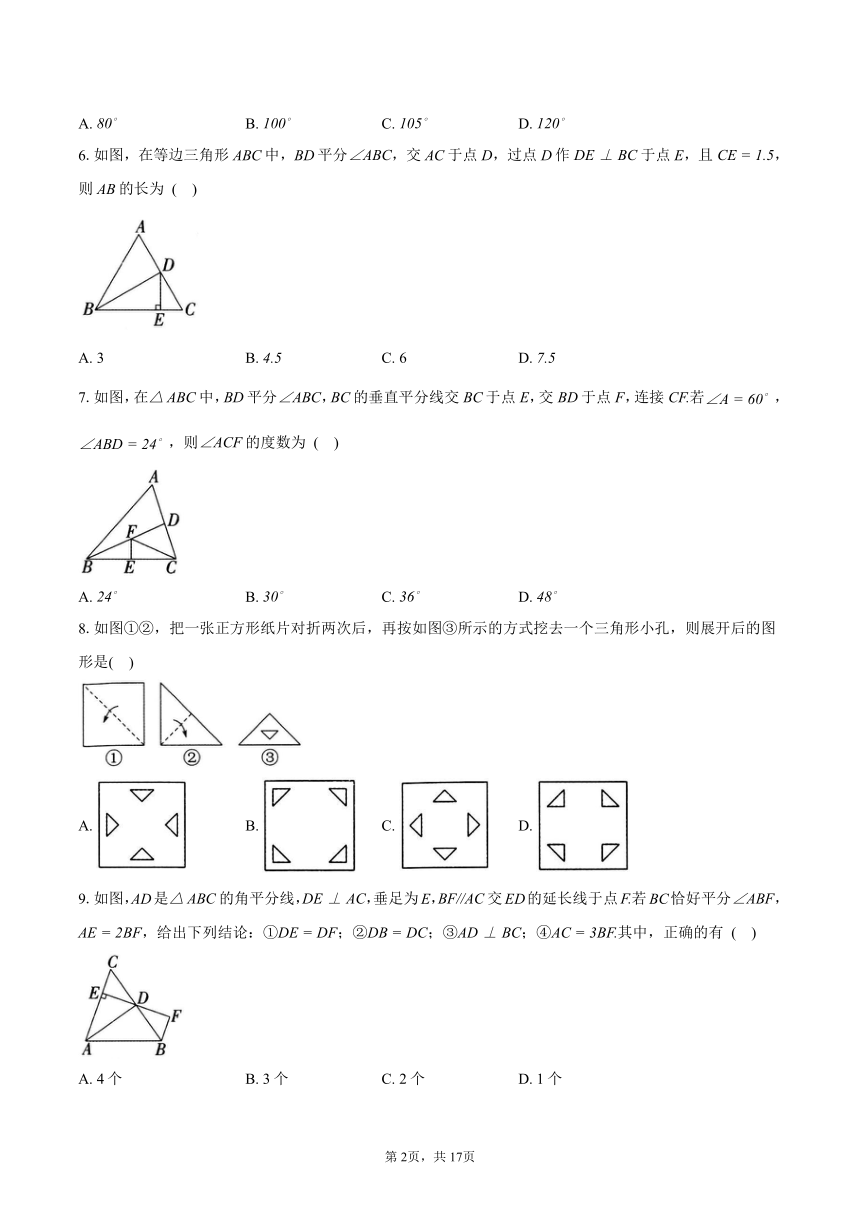
6.如图,在等边三角形ABC中,BD平分,交AC于点D,过点D作于点E,且,则AB的长为 ( )
A. 3 B. C. 6 D.
7.如图,在中,BD平分,BC的垂直平分线交BC于点E,交BD于点F,连接若,,则的度数为 ( )
A. B. C. D.
8.如图①②,把一张正方形纸片对折两次后,再按如图③所示的方式挖去一个三角形小孔,则展开后的图形是( )
A. B. C. D.
9.如图,AD是的角平分线,,垂足为E,交ED的延长线于点若BC恰好平分,,给出下列结论:①;②;③;④其中,正确的有 ( )
A. 4个 B. 3个 C. 2个 D. 1个
10.如图,点E在等边三角形ABC的边BC上,,射线于点C,P是射线CD上一动点,F是线段AB上一动点,当的值最小时,,则AC的长为 ( )
A. 10 B. 12 C. 13 D. 14
二、填空题:本题共8小题,每小题3分,共24分。
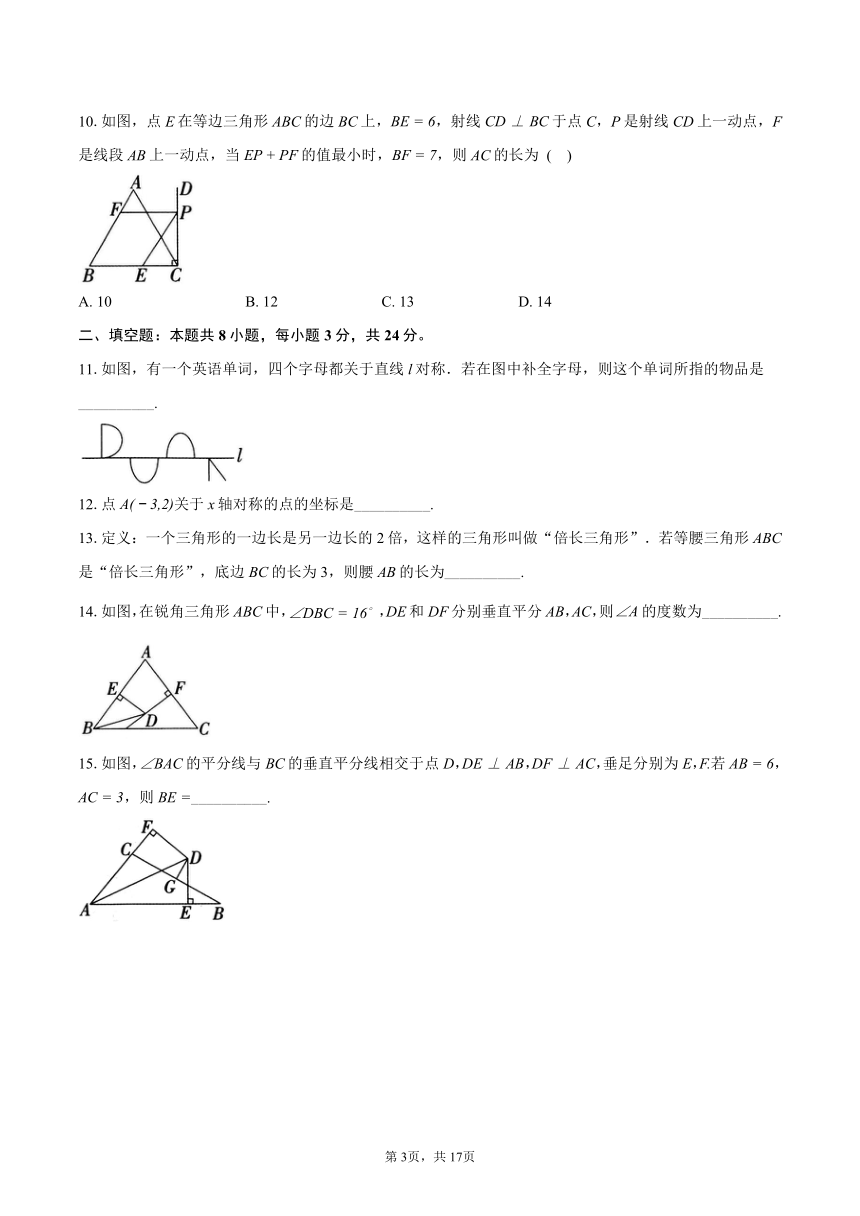
11.如图,有一个英语单词,四个字母都关于直线l对称.若在图中补全字母,则这个单词所指的物品是__________.
12.点关于x轴对称的点的坐标是__________.
13.定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫做“倍长三角形”.若等腰三角形ABC是“倍长三角形”,底边BC的长为3,则腰AB的长为__________.
14.如图,在锐角三角形ABC中,,DE和DF分别垂直平分AB,AC,则的度数为__________.
15.如图,的平分线与BC的垂直平分线相交于点D,,,垂足分别为E,若,,则__________.
16.如图,在中,,,,C,D分别是线段BE,AE上的动点,且,则CD长的取值范围是__________.
17.如图,O是等边三角形ABC内一点,D是线段BO延长线上一点,且,,则__________.
18.如图,在锐角三角形ABC中,,,,P是边BC上的动点,点P关于直线AB,AC的对称点分别是M,N,连接MN,则MN长的最小值为__________.
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
19.本小题8分
如图,在平面直角坐标系中,的顶点坐标分别为,,
把向下平移4个单位长度,再以y轴为对称轴对称,得到,请你画出;
分别写出A,B,C三点的对应点,,的坐标.
20.本小题8分
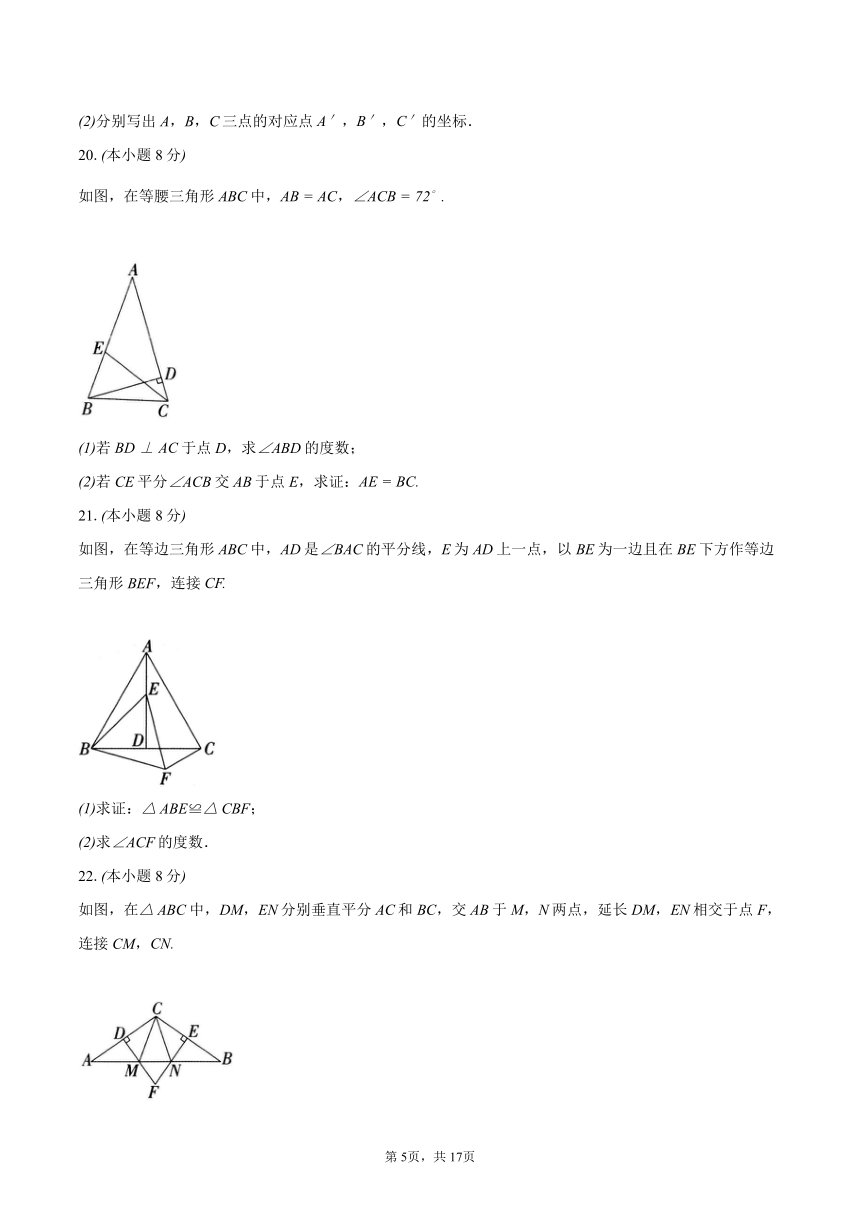
如图,在等腰三角形ABC中,,
若于点D,求的度数;
若CE平分交AB于点E,求证:
21.本小题8分
如图,在等边三角形ABC中,AD是的平分线,E为AD上一点,以BE为一边且在BE下方作等边三角形BEF,连接
求证:≌;
求的度数.
22.本小题8分
如图,在中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,延长DM,EN相交于点F,连接CM,
若的周长为15 cm,求AB的长;
若,求的度数.
23.本小题8分
在中,,,点P在边BC上运动不与点B,C重合,连接AP,作,PQ交AB于点
如图,当时,判断的形状,并说明理由.
在点P的运动过程中,的形状可以是等腰三角形吗?若可以,请求出的度数;若不可以,请说明理由.
24.本小题8分
如图,在平面直角坐标系中,作直线轴于点,已知,,以AB为斜边作等腰直角三角形ABC,点C在第一象限,关于直线l对称的图形是给出如下定义:如果点M在的内部或边上,那么称M是关于直线l的“称心点”.
当时,在点,,中,关于直线l的“称心点”是__________;
当的边上只有1个点是关于直线l的“称心点”时,直接写出a的值;
若H是关于直线l的“称心点”,且总有的面积大于的面积,求a的取值范围.
答案和解析
1.【答案】A
【解析】略
2.【答案】A
【解析】【分析】
本题考查了等腰三角形的性质,三角形的内角和定理.解题的关键在于明确该三角形为钝角等腰三角形.由题意知,的内角为等腰三角形的顶角,进而可求底角.
【解答】
解:在一个内角是的等腰三角形中,该内角必为顶角,
底角的度数为
故选
3.【答案】C
【解析】解:连接,
与关于直线EF对称,
≌,
,,
,
,
,
,
,
故选:
利用轴对称图形的性质得出≌,进而结合三角形内角和定理得出答案.
此题主要考查了轴对称图形的性质以及等腰三角形,正确得出度数是解题关键.
4.【答案】A
【解析】解:如图,
,,
,
,,
,
,
故选:
利用等腰三角形的性质得到,利用平行线的性质得到,再根据三角形外角的性质即可求解.
本题考查了等腰三角形的性质,平行线的性质以及三角形外角的性质,解决问题的关键是注意运用两直线平行,同旁内角互补.
5.【答案】B
【解析】解:连接OA,
为三边垂直平分线的交点,
,
,,
,
,
,
,
故选:
连接OA,根据线段垂直平分线的性质得到,根据等腰三角形的性质、三角形内角和定理计算即可.
本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
6.【答案】C
【解析】【分析】
此题考查了等边三角形的性质,含角的直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用,
由在等边三角形ABC中,,可求得,则可求得CD的长,又由BD平分交AC于点D,由三线合一的知识,即可求得答案.
【解答】
解:是等边三角形,
,,
,
在中,,
,
,
平分交AC于点D,且
,
故选
7.【答案】D
【解析】【分析】
根据角平分线的性质可得,然后再计算出的度数,再根据线段垂直平分线的性质可得,进而可得,然后可算出的度数.
此题主要考查了线段垂直平分线的性质,以及三角形内角和定理,关键是掌握线段垂直平分线上任意一点,到线段两端点的距离相等.
【解答】
解:平分,
,
,
,
的中垂线交BC于点E,交BD于点F,
,
,
,
故选:
8.【答案】C
【解析】略
9.【答案】A
【解析】【分析】
本题考查了全等三角形的判定和性质,等腰三角形的性质,平行线的性质,掌握等腰三角形的性质三线合一是解题的关键.根据等腰三角形的性质三线合一得到,,故②③正确;通过≌,得到,,故①④正确.
【解答】
解:,
,
平分,
,
,
,
是的角平分线,
,,故②③正确,
在与中,
,,,
≌,
,,故①正确;
,
,故④正确.
故选
10.【答案】A
【解析】略
11.【答案】书
【解析】【分析】
本题考查了轴对称图形,解决本题的关键是根据轴对称的性质,作出图形.
根据轴对称图形的性质,组成图形,即可解答.
【解答】
解:如图,
这个单词所指的物品是书.
故答案为书.
12.【答案】
【解析】略
13.【答案】6
【解析】解:等腰是“倍长三角形”,
或,
若,则三边分别是6,6,3,符合题意,
腰AB的长为6;
若,则,三边分别是,,3,
,
此时不能构成三角形,这种情况不存在;
综上所述,腰AB的长是6,
故答案为:
由等腰是“倍长三角形”,可知或,若,可得AB的长为6;若,因,故此时不能构成三角形,这种情况不存在;即可得答案.
本题考查三角形三边关系,涉及新定义,解题的关键是分类思想的应用及掌握三角形任意两边的和大于第三边.
14.【答案】
【解析】【分析】
本题主要考查了线段垂直平分线的性质、等腰三角形的性质、三角形的内角和定理以及角的和差计算,熟练掌握线段垂直平分线的性质以及等腰三角形的性质是解决本题的关键.
连接DC,AD,先根据线段垂直平分线的性质以及等腰三角形的性质得出,,,再根据角的和差以及三角形的内角和定理列出关于的方程即可求解.
【解答】
解:连接DC,AD,
和DF分别垂直平分AB,AC,
,
,,,
,
,,
,
,
,
解得:
故答案为:
15.【答案】
【解析】【分析】
此题考查了线段垂直平分线的性质、角平分线的性质以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法、数形结合思想的应用.
连接CD,BD,根据角平分线的性质与线段垂直平分线的性质,易得,,证明,可得;证明,可得,进而可得,即可求得答案.
【解答】
解:连接CD,BD,
是的平分线,,,
,,
又,
,
,
是BC的垂直平分线,
,
在和中,
,
,
,
,
,,
故答案为
16.【答案】
【解析】【分析】
略
【解答】
略
17.【答案】
【解析】略
18.【答案】
【解析】略
19.【答案】【小题1】如图,即为所求:
【小题2】,,
【解析】略
略
20.【答案】【小题1】在等腰三角形ABC中,,,于点D,
【小题2】在等腰三角形ABC中,,,,平分,,
【解析】略
略
21.【答案】【小题1】是等边三角形,,是等边三角形,,在和中, ≌
【小题2】是等边三角形,AD是的平分线,,≌,
【解析】略
略
22.【答案】【小题1】,FN分别垂直平分AC和BC,,的周长的周长为15 cm,
【小题2】,,,,,,
【解析】略
略
23.【答案】【小题1】是直角三角形
理由:,,
,
是直角三角形.
【小题2】可以
当时,,
当时,,
当时,
点P不与点B,C重合,
这种情况不存在.
综上所述,或
【解析】略
略
24.【答案】【小题1】
D;E
【小题2】
【小题3】
如图,作,作轴,交AF于点,延长AC至点D,使,作,作轴,交DE于点,连接,
当C与是对称点时,,此时;
当B与是对称点时,,此时
当或时,总有的面积大于的面积.
【解析】略
略
略
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列“绿色食品、响应环保、可回收物、节水”四个标志图案中,属于轴对称图形的是( )
A. B. C. D.
2.等腰三角形的一个内角的度数是,则其底角的度数是( )
A. B. C. D. 或
3.如图,在中,,,与关于直线EF对称,,连接,则的度数是 ( )
A. B. C. D.
4.如图,直线,点A在直线上,点B在直线上,,,,则的度数是 ( )
A. B. C. D.
5.如图,O为三边垂直平分线的交点,且,则的度数为 ( )
A. B. C. D.
6.如图,在等边三角形ABC中,BD平分,交AC于点D,过点D作于点E,且,则AB的长为 ( )
A. 3 B. C. 6 D.
7.如图,在中,BD平分,BC的垂直平分线交BC于点E,交BD于点F,连接若,,则的度数为 ( )
A. B. C. D.
8.如图①②,把一张正方形纸片对折两次后,再按如图③所示的方式挖去一个三角形小孔,则展开后的图形是( )
A. B. C. D.
9.如图,AD是的角平分线,,垂足为E,交ED的延长线于点若BC恰好平分,,给出下列结论:①;②;③;④其中,正确的有 ( )
A. 4个 B. 3个 C. 2个 D. 1个
10.如图,点E在等边三角形ABC的边BC上,,射线于点C,P是射线CD上一动点,F是线段AB上一动点,当的值最小时,,则AC的长为 ( )
A. 10 B. 12 C. 13 D. 14
二、填空题:本题共8小题,每小题3分,共24分。
11.如图,有一个英语单词,四个字母都关于直线l对称.若在图中补全字母,则这个单词所指的物品是__________.
12.点关于x轴对称的点的坐标是__________.
13.定义:一个三角形的一边长是另一边长的2倍,这样的三角形叫做“倍长三角形”.若等腰三角形ABC是“倍长三角形”,底边BC的长为3,则腰AB的长为__________.
14.如图,在锐角三角形ABC中,,DE和DF分别垂直平分AB,AC,则的度数为__________.
15.如图,的平分线与BC的垂直平分线相交于点D,,,垂足分别为E,若,,则__________.
16.如图,在中,,,,C,D分别是线段BE,AE上的动点,且,则CD长的取值范围是__________.
17.如图,O是等边三角形ABC内一点,D是线段BO延长线上一点,且,,则__________.
18.如图,在锐角三角形ABC中,,,,P是边BC上的动点,点P关于直线AB,AC的对称点分别是M,N,连接MN,则MN长的最小值为__________.
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
19.本小题8分
如图,在平面直角坐标系中,的顶点坐标分别为,,
把向下平移4个单位长度,再以y轴为对称轴对称,得到,请你画出;
分别写出A,B,C三点的对应点,,的坐标.
20.本小题8分
如图,在等腰三角形ABC中,,
若于点D,求的度数;
若CE平分交AB于点E,求证:
21.本小题8分
如图,在等边三角形ABC中,AD是的平分线,E为AD上一点,以BE为一边且在BE下方作等边三角形BEF,连接
求证:≌;
求的度数.
22.本小题8分
如图,在中,DM,EN分别垂直平分AC和BC,交AB于M,N两点,延长DM,EN相交于点F,连接CM,
若的周长为15 cm,求AB的长;
若,求的度数.
23.本小题8分
在中,,,点P在边BC上运动不与点B,C重合,连接AP,作,PQ交AB于点
如图,当时,判断的形状,并说明理由.
在点P的运动过程中,的形状可以是等腰三角形吗?若可以,请求出的度数;若不可以,请说明理由.
24.本小题8分
如图,在平面直角坐标系中,作直线轴于点,已知,,以AB为斜边作等腰直角三角形ABC,点C在第一象限,关于直线l对称的图形是给出如下定义:如果点M在的内部或边上,那么称M是关于直线l的“称心点”.
当时,在点,,中,关于直线l的“称心点”是__________;
当的边上只有1个点是关于直线l的“称心点”时,直接写出a的值;
若H是关于直线l的“称心点”,且总有的面积大于的面积,求a的取值范围.
答案和解析
1.【答案】A
【解析】略
2.【答案】A
【解析】【分析】
本题考查了等腰三角形的性质,三角形的内角和定理.解题的关键在于明确该三角形为钝角等腰三角形.由题意知,的内角为等腰三角形的顶角,进而可求底角.
【解答】
解:在一个内角是的等腰三角形中,该内角必为顶角,
底角的度数为
故选
3.【答案】C
【解析】解:连接,
与关于直线EF对称,
≌,
,,
,
,
,
,
,
故选:
利用轴对称图形的性质得出≌,进而结合三角形内角和定理得出答案.
此题主要考查了轴对称图形的性质以及等腰三角形,正确得出度数是解题关键.
4.【答案】A
【解析】解:如图,
,,
,
,,
,
,
故选:
利用等腰三角形的性质得到,利用平行线的性质得到,再根据三角形外角的性质即可求解.
本题考查了等腰三角形的性质,平行线的性质以及三角形外角的性质,解决问题的关键是注意运用两直线平行,同旁内角互补.
5.【答案】B
【解析】解:连接OA,
为三边垂直平分线的交点,
,
,,
,
,
,
,
故选:
连接OA,根据线段垂直平分线的性质得到,根据等腰三角形的性质、三角形内角和定理计算即可.
本题考查的是线段的垂直平分线的性质,掌握线段的垂直平分线上的点到线段的两个端点的距离相等是解题的关键.
6.【答案】C
【解析】【分析】
此题考查了等边三角形的性质,含角的直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用,
由在等边三角形ABC中,,可求得,则可求得CD的长,又由BD平分交AC于点D,由三线合一的知识,即可求得答案.
【解答】
解:是等边三角形,
,,
,
在中,,
,
,
平分交AC于点D,且
,
故选
7.【答案】D
【解析】【分析】
根据角平分线的性质可得,然后再计算出的度数,再根据线段垂直平分线的性质可得,进而可得,然后可算出的度数.
此题主要考查了线段垂直平分线的性质,以及三角形内角和定理,关键是掌握线段垂直平分线上任意一点,到线段两端点的距离相等.
【解答】
解:平分,
,
,
,
的中垂线交BC于点E,交BD于点F,
,
,
,
故选:
8.【答案】C
【解析】略
9.【答案】A
【解析】【分析】
本题考查了全等三角形的判定和性质,等腰三角形的性质,平行线的性质,掌握等腰三角形的性质三线合一是解题的关键.根据等腰三角形的性质三线合一得到,,故②③正确;通过≌,得到,,故①④正确.
【解答】
解:,
,
平分,
,
,
,
是的角平分线,
,,故②③正确,
在与中,
,,,
≌,
,,故①正确;
,
,故④正确.
故选
10.【答案】A
【解析】略
11.【答案】书
【解析】【分析】
本题考查了轴对称图形,解决本题的关键是根据轴对称的性质,作出图形.
根据轴对称图形的性质,组成图形,即可解答.
【解答】
解:如图,
这个单词所指的物品是书.
故答案为书.
12.【答案】
【解析】略
13.【答案】6
【解析】解:等腰是“倍长三角形”,
或,
若,则三边分别是6,6,3,符合题意,
腰AB的长为6;
若,则,三边分别是,,3,
,
此时不能构成三角形,这种情况不存在;
综上所述,腰AB的长是6,
故答案为:
由等腰是“倍长三角形”,可知或,若,可得AB的长为6;若,因,故此时不能构成三角形,这种情况不存在;即可得答案.
本题考查三角形三边关系,涉及新定义,解题的关键是分类思想的应用及掌握三角形任意两边的和大于第三边.
14.【答案】
【解析】【分析】
本题主要考查了线段垂直平分线的性质、等腰三角形的性质、三角形的内角和定理以及角的和差计算,熟练掌握线段垂直平分线的性质以及等腰三角形的性质是解决本题的关键.
连接DC,AD,先根据线段垂直平分线的性质以及等腰三角形的性质得出,,,再根据角的和差以及三角形的内角和定理列出关于的方程即可求解.
【解答】
解:连接DC,AD,
和DF分别垂直平分AB,AC,
,
,,,
,
,,
,
,
,
解得:
故答案为:
15.【答案】
【解析】【分析】
此题考查了线段垂直平分线的性质、角平分线的性质以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法、数形结合思想的应用.
连接CD,BD,根据角平分线的性质与线段垂直平分线的性质,易得,,证明,可得;证明,可得,进而可得,即可求得答案.
【解答】
解:连接CD,BD,
是的平分线,,,
,,
又,
,
,
是BC的垂直平分线,
,
在和中,
,
,
,
,
,,
故答案为
16.【答案】
【解析】【分析】
略
【解答】
略
17.【答案】
【解析】略
18.【答案】
【解析】略
19.【答案】【小题1】如图,即为所求:
【小题2】,,
【解析】略
略
20.【答案】【小题1】在等腰三角形ABC中,,,于点D,
【小题2】在等腰三角形ABC中,,,,平分,,
【解析】略
略
21.【答案】【小题1】是等边三角形,,是等边三角形,,在和中, ≌
【小题2】是等边三角形,AD是的平分线,,≌,
【解析】略
略
22.【答案】【小题1】,FN分别垂直平分AC和BC,,的周长的周长为15 cm,
【小题2】,,,,,,
【解析】略
略
23.【答案】【小题1】是直角三角形
理由:,,
,
是直角三角形.
【小题2】可以
当时,,
当时,,
当时,
点P不与点B,C重合,
这种情况不存在.
综上所述,或
【解析】略
略
24.【答案】【小题1】
D;E
【小题2】
【小题3】
如图,作,作轴,交AF于点,延长AC至点D,使,作,作轴,交DE于点,连接,
当C与是对称点时,,此时;
当B与是对称点时,,此时
当或时,总有的面积大于的面积.
【解析】略
略
略
第1页,共1页
