第十一章 三角形 单元测试(含解析)2024-2025学年数学人教版八年级上册
文档属性
| 名称 | 第十一章 三角形 单元测试(含解析)2024-2025学年数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 372.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-21 10:27:09 | ||
图片预览



文档简介
第十一章三角形
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
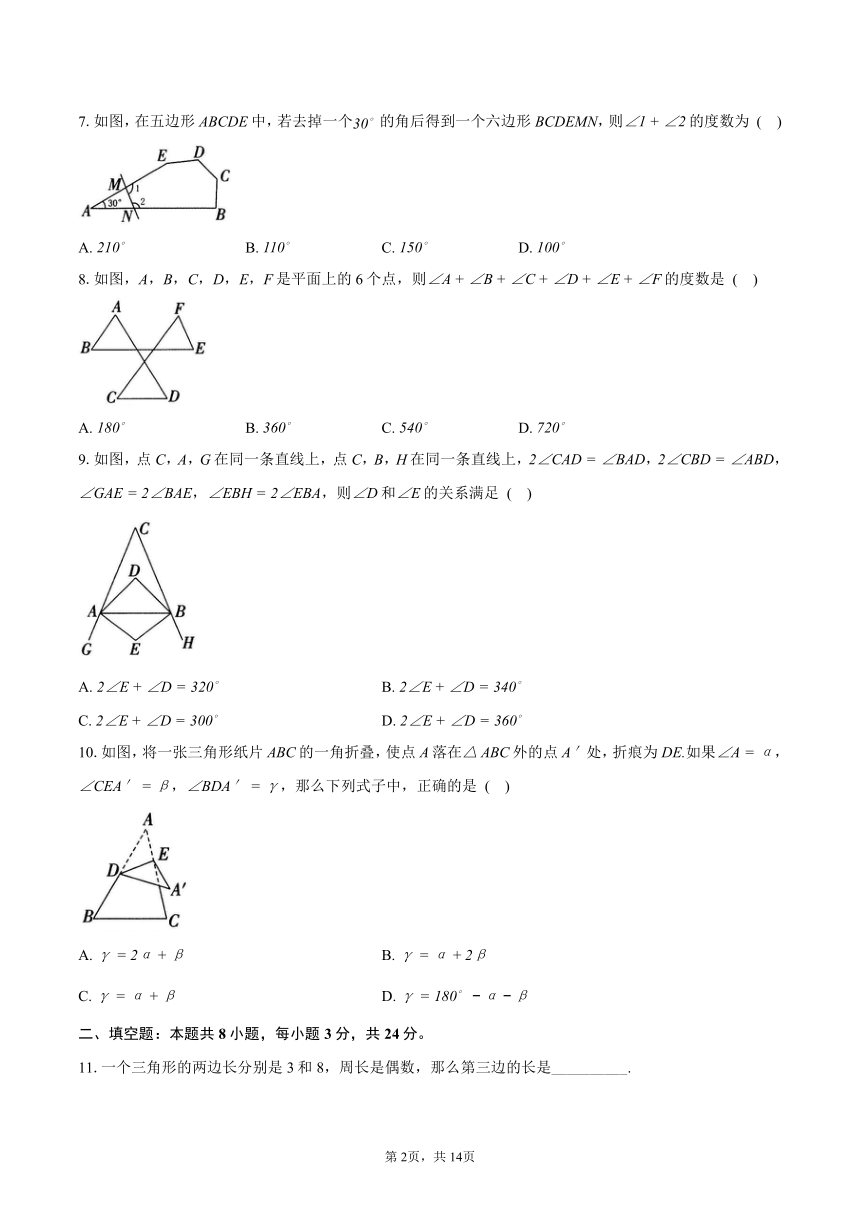
1.下列长度的两条线段与长度为6的线段能组成三角形的是( )
A. 1,4 B. 3,3 C. 4,6 D. 2,4
2.下列四个图形中,BE不是的高的为 ( )
A. B.
C. D.
3.正多边形的每个内角的度数为,则它的边数是( )
A. 4 B. 6 C. 7 D. 5
4.在中,若,,则的度数为 ( )
A. B. C. D.
5.如图,在五边形ABCDE中,若,则的度数为 ( )
A. B. C. D.
6.如图,直线,,,则的度数是 ( )
A. B. C. D.
7.如图,在五边形ABCDE中,若去掉一个的角后得到一个六边形BCDEMN,则的度数为 ( )
A. B. C. D.
8.如图,A,B,C,D,E,F是平面上的6个点,则的度数是 ( )
A. B. C. D.
9.如图,点C,A,G在同一条直线上,点C,B,H在同一条直线上,,,,,则和的关系满足 ( )
A. B.
C. D.
10.如图,将一张三角形纸片ABC的一角折叠,使点A落在外的点处,折痕为如果,,,那么下列式子中,正确的是 ( )
A. B.
C. D.
二、填空题:本题共8小题,每小题3分,共24分。
11.一个三角形的两边长分别是3和8,周长是偶数,那么第三边的长是__________.
12.如图,的周长为24 cm,,边BC上的中线,的周长为18 cm,则__________
13.已知一个多边形的每个外角度数都等于相邻内角度数的,则该多边形的边数为__________.
14.如图,在中,,沿CD折叠,使点B恰好落在边AC上的点E处.若,则的度数为__________.
15.如图,在中,AD,BE分别是的高和角平分线.若,,则__________.
16.如图,直线,分别经过正六边形ABCDEF的顶点A,B,且若,则__________用含的式子表示
17.如图,在中,BD平分,E为BD上一点,于点若,,则的度数为__________.
18.如图,在四边形ABCD中,,,分别是和的邻补角,则__________.
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
19.本小题8分
如图,在中,为钝角,请依次完成下列各题:
画出边BC上的中线AD;
画出边AC上的高BH;
图中共有__________个三角形,其中面积一定相等的三角形是__________.
20.本小题8分
已知一个多边形的内角和与外角和相加是,求这个多边形的边数.
21.本小题8分
如图,在中,,,
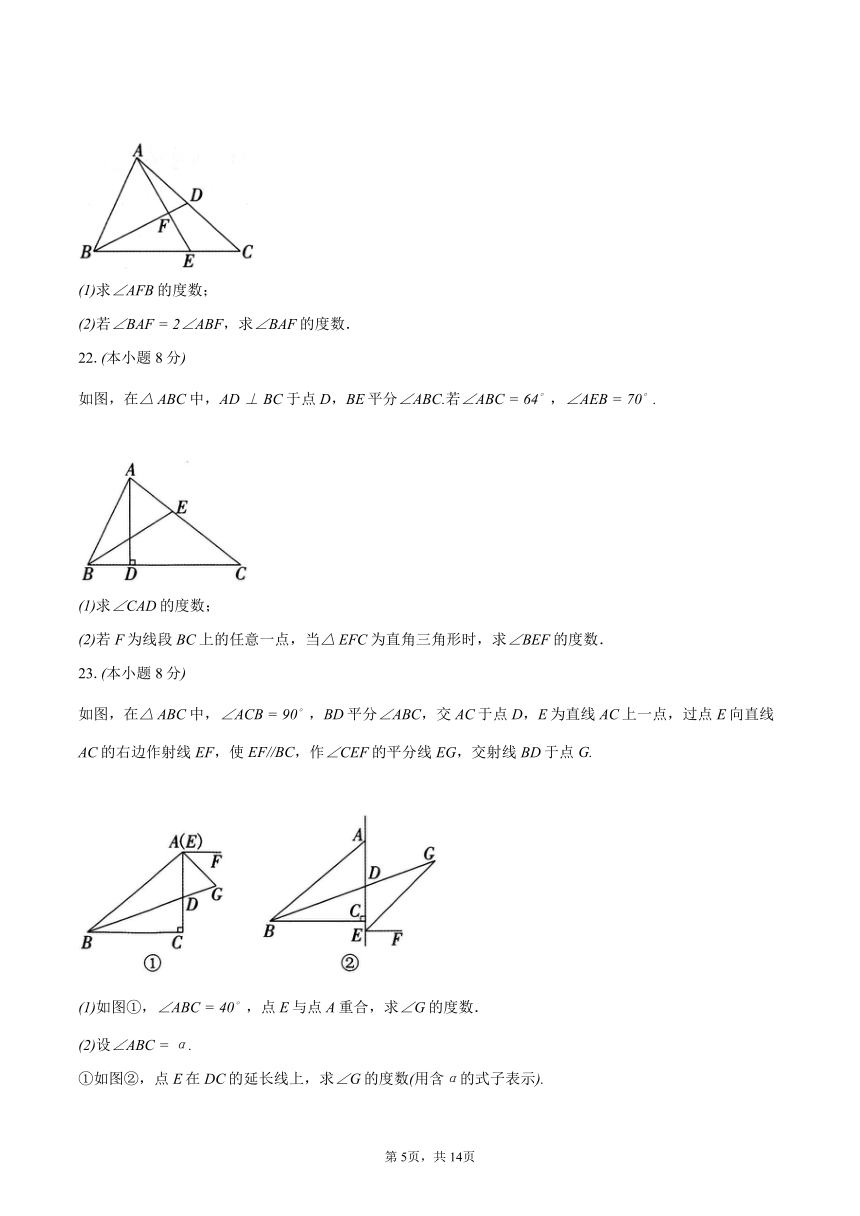
求的度数;
若,求的度数.
22.本小题8分
如图,在中,于点D,BE平分若,
求的度数;
若F为线段BC上的任意一点,当为直角三角形时,求的度数.
23.本小题8分
如图,在中,,BD平分,交AC于点D,E为直线AC上一点,过点E向直线AC的右边作射线EF,使,作的平分线EG,交射线BD于点
如图①,,点E与点A重合,求的度数.
设
①如图②,点E在DC的延长线上,求的度数用含的式子表示
②点E在直线AC上滑动,当存在时,其度数是否发生变化?若不变,请说明理由;若变化,请直接用含的式子表示的度数.
24.本小题8分
在中,若存在一个内角角度是另外一个内角角度的n倍为大于1的正整数,则称为n倍角三角形.例如:在中,,,,可知,所以为3倍角三角形.
在中,,,则为__________倍角三角形.
若锐角三角形MNP是3倍角三角形,且最小内角为,请直接写出的取值范围:__________.
如图,直线于点O,点A在射线OP上运动不与点O重合,点B在射线OM上运动不与点O重合,延长BA至点G,,的平分线与的平分线所在的直线分别相交于点E,若为4倍角三角形,求的度数.
答案和解析
1.【答案】C
【解析】【分析】
本题考查的是三角形的三边关系,熟练掌握三角形的三边关系是解题额关键.
根据三角形的三边关系逐项分析即可.
【解答】
解:因为,所以此两条线段与长度为6的线段不能组成三角形,故A不符合题意;
因为,所以此两条线段与长度为6的线段不能组成三角形,故B不符合题意;
因为,,所以此两条线段与长度为6的线段能组成三角形,故C符合题意;
因为,所以此两条线段与长度为6的线段不能组成三角形,故D不符合题意.
2.【答案】C
【解析】略
3.【答案】D
【解析】略
4.【答案】A
【解析】略
5.【答案】B
【解析】解:,
的外角是,
多边形的外角和等于,
故选:
多边形的外角和等于,由此即可计算.
本题考查多边形的有关知识,关键是掌握多边形的外角和等于
6.【答案】C
【解析】略
7.【答案】A
【解析】解:,,
,
,
,
故选:
根据多变的内角和定理可求解,,进而可求解.
本题主要考查多边形的内角和外角,掌握多边形的内角和定理是解题的关键.
8.【答案】B
【解析】【分析】
本题考查的是三角形外角的性质及三角形的外角和,熟知三角形的外角和是360度是解答此题的关键.
先根据三角形外角的性质得出,,,再根据三角形的外角和是进行解答.
【解答】
解:是的外角,
,
是的外角,
,
是的外角,
,
、、是的外角,
,
故选:
9.【答案】C
【解析】略
10.【答案】A
【解析】【分析】
本题主要考查了三角形的外角性质,折叠的性质,关键是熟练掌握折叠的性质.
先根据折叠的性质得出,然后根据三角形的外角性质进行计算即可.
【解答】
解:如图,设AC与交于点F,
由折叠的性质得:,
,,
,
,,,
故选
11.【答案】7或
【解析】【分析】
本题主要考查的是三角形的三边关系和特殊解,注意:偶数加偶数为偶数,奇数加奇数为偶数,难度适中.
本题可先求出第三边的取值范围.再根据为奇数,周长为偶数,可知第三边为奇数,从而找出取值范围中的奇数,即为第三边的长.
【解答】
解:设第三边长为x,
则,即
又为奇数,
或9,
故答案为7或
12.【答案】8
【解析】略
13.【答案】6
【解析】略
14.【答案】
【解析】略
15.【答案】
【解析】略
16.【答案】
【解析】【分析】
此题考查的知识点是平行线的性质及正多边形的性质,解题的关键是由正多边形的性质和已知得出答案.根据正六边形的内角和平行线的性质解答即可.
【解答】
解:因为六五边形ABCDE的一个内角是,
且,,
,
,
故答案为:
17.【答案】
【解析】略
18.【答案】
【解析】略
19.【答案】【小题1】
如图,线段AD即为所求
【小题2】
如图,线段BH即为所求
【小题3】
5
;
【解析】略
略
略
20.【答案】解:设这个多边形的边数是n,
则,
解得
故这个多边形的边数为
【解析】本题考查了多边形的内角和与外角和定理,任意多边形的外角和都是,与边数无关.依题意,多边形的内角和与外角和共为,多边形的外角和为,根据内角和公式求出多边形的边数.
21.【答案】【小题1】,,,
,
【小题2】
,,
【解析】略
略
22.【答案】【小题1】平分,, ,,
【小题2】①当时,②当时,,综上所述,的度数为或
【解析】略
略
23.【答案】【小题1】如图①,过点G作于点H,则
,,
平分,EG平分,
, .
【小题2】①如图②,过点G作于点H,则
由,易知 ,
②变化
当点E在点D下方时, ;
当点E在点D上方时,
【解析】略
略
24.【答案】【小题1】
2
【小题2】
【小题3】
解:平分,AF平分,
,
.
是4倍角三角形,显然大于,
或
或
平分,OE平分,
易得 .
的度数为或
【解析】略
略
略
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列长度的两条线段与长度为6的线段能组成三角形的是( )
A. 1,4 B. 3,3 C. 4,6 D. 2,4
2.下列四个图形中,BE不是的高的为 ( )
A. B.
C. D.
3.正多边形的每个内角的度数为,则它的边数是( )
A. 4 B. 6 C. 7 D. 5
4.在中,若,,则的度数为 ( )
A. B. C. D.
5.如图,在五边形ABCDE中,若,则的度数为 ( )
A. B. C. D.
6.如图,直线,,,则的度数是 ( )
A. B. C. D.
7.如图,在五边形ABCDE中,若去掉一个的角后得到一个六边形BCDEMN,则的度数为 ( )
A. B. C. D.
8.如图,A,B,C,D,E,F是平面上的6个点,则的度数是 ( )
A. B. C. D.
9.如图,点C,A,G在同一条直线上,点C,B,H在同一条直线上,,,,,则和的关系满足 ( )
A. B.
C. D.
10.如图,将一张三角形纸片ABC的一角折叠,使点A落在外的点处,折痕为如果,,,那么下列式子中,正确的是 ( )
A. B.
C. D.
二、填空题:本题共8小题,每小题3分,共24分。
11.一个三角形的两边长分别是3和8,周长是偶数,那么第三边的长是__________.
12.如图,的周长为24 cm,,边BC上的中线,的周长为18 cm,则__________
13.已知一个多边形的每个外角度数都等于相邻内角度数的,则该多边形的边数为__________.
14.如图,在中,,沿CD折叠,使点B恰好落在边AC上的点E处.若,则的度数为__________.
15.如图,在中,AD,BE分别是的高和角平分线.若,,则__________.
16.如图,直线,分别经过正六边形ABCDEF的顶点A,B,且若,则__________用含的式子表示
17.如图,在中,BD平分,E为BD上一点,于点若,,则的度数为__________.
18.如图,在四边形ABCD中,,,分别是和的邻补角,则__________.
三、解答题:本题共6小题,共48分。解答应写出文字说明,证明过程或演算步骤。
19.本小题8分
如图,在中,为钝角,请依次完成下列各题:
画出边BC上的中线AD;
画出边AC上的高BH;
图中共有__________个三角形,其中面积一定相等的三角形是__________.
20.本小题8分
已知一个多边形的内角和与外角和相加是,求这个多边形的边数.
21.本小题8分
如图,在中,,,
求的度数;
若,求的度数.
22.本小题8分
如图,在中,于点D,BE平分若,
求的度数;
若F为线段BC上的任意一点,当为直角三角形时,求的度数.
23.本小题8分
如图,在中,,BD平分,交AC于点D,E为直线AC上一点,过点E向直线AC的右边作射线EF,使,作的平分线EG,交射线BD于点
如图①,,点E与点A重合,求的度数.
设
①如图②,点E在DC的延长线上,求的度数用含的式子表示
②点E在直线AC上滑动,当存在时,其度数是否发生变化?若不变,请说明理由;若变化,请直接用含的式子表示的度数.
24.本小题8分
在中,若存在一个内角角度是另外一个内角角度的n倍为大于1的正整数,则称为n倍角三角形.例如:在中,,,,可知,所以为3倍角三角形.
在中,,,则为__________倍角三角形.
若锐角三角形MNP是3倍角三角形,且最小内角为,请直接写出的取值范围:__________.
如图,直线于点O,点A在射线OP上运动不与点O重合,点B在射线OM上运动不与点O重合,延长BA至点G,,的平分线与的平分线所在的直线分别相交于点E,若为4倍角三角形,求的度数.
答案和解析
1.【答案】C
【解析】【分析】
本题考查的是三角形的三边关系,熟练掌握三角形的三边关系是解题额关键.
根据三角形的三边关系逐项分析即可.
【解答】
解:因为,所以此两条线段与长度为6的线段不能组成三角形,故A不符合题意;
因为,所以此两条线段与长度为6的线段不能组成三角形,故B不符合题意;
因为,,所以此两条线段与长度为6的线段能组成三角形,故C符合题意;
因为,所以此两条线段与长度为6的线段不能组成三角形,故D不符合题意.
2.【答案】C
【解析】略
3.【答案】D
【解析】略
4.【答案】A
【解析】略
5.【答案】B
【解析】解:,
的外角是,
多边形的外角和等于,
故选:
多边形的外角和等于,由此即可计算.
本题考查多边形的有关知识,关键是掌握多边形的外角和等于
6.【答案】C
【解析】略
7.【答案】A
【解析】解:,,
,
,
,
故选:
根据多变的内角和定理可求解,,进而可求解.
本题主要考查多边形的内角和外角,掌握多边形的内角和定理是解题的关键.
8.【答案】B
【解析】【分析】
本题考查的是三角形外角的性质及三角形的外角和,熟知三角形的外角和是360度是解答此题的关键.
先根据三角形外角的性质得出,,,再根据三角形的外角和是进行解答.
【解答】
解:是的外角,
,
是的外角,
,
是的外角,
,
、、是的外角,
,
故选:
9.【答案】C
【解析】略
10.【答案】A
【解析】【分析】
本题主要考查了三角形的外角性质,折叠的性质,关键是熟练掌握折叠的性质.
先根据折叠的性质得出,然后根据三角形的外角性质进行计算即可.
【解答】
解:如图,设AC与交于点F,
由折叠的性质得:,
,,
,
,,,
故选
11.【答案】7或
【解析】【分析】
本题主要考查的是三角形的三边关系和特殊解,注意:偶数加偶数为偶数,奇数加奇数为偶数,难度适中.
本题可先求出第三边的取值范围.再根据为奇数,周长为偶数,可知第三边为奇数,从而找出取值范围中的奇数,即为第三边的长.
【解答】
解:设第三边长为x,
则,即
又为奇数,
或9,
故答案为7或
12.【答案】8
【解析】略
13.【答案】6
【解析】略
14.【答案】
【解析】略
15.【答案】
【解析】略
16.【答案】
【解析】【分析】
此题考查的知识点是平行线的性质及正多边形的性质,解题的关键是由正多边形的性质和已知得出答案.根据正六边形的内角和平行线的性质解答即可.
【解答】
解:因为六五边形ABCDE的一个内角是,
且,,
,
,
故答案为:
17.【答案】
【解析】略
18.【答案】
【解析】略
19.【答案】【小题1】
如图,线段AD即为所求
【小题2】
如图,线段BH即为所求
【小题3】
5
;
【解析】略
略
略
20.【答案】解:设这个多边形的边数是n,
则,
解得
故这个多边形的边数为
【解析】本题考查了多边形的内角和与外角和定理,任意多边形的外角和都是,与边数无关.依题意,多边形的内角和与外角和共为,多边形的外角和为,根据内角和公式求出多边形的边数.
21.【答案】【小题1】,,,
,
【小题2】
,,
【解析】略
略
22.【答案】【小题1】平分,, ,,
【小题2】①当时,②当时,,综上所述,的度数为或
【解析】略
略
23.【答案】【小题1】如图①,过点G作于点H,则
,,
平分,EG平分,
, .
【小题2】①如图②,过点G作于点H,则
由,易知 ,
②变化
当点E在点D下方时, ;
当点E在点D上方时,
【解析】略
略
24.【答案】【小题1】
2
【小题2】
【小题3】
解:平分,AF平分,
,
.
是4倍角三角形,显然大于,
或
或
平分,OE平分,
易得 .
的度数为或
【解析】略
略
略
第1页,共1页
