湖北省武汉市外国语学校2024-2025学年八年级上学期10月月考数学试题(含答案)
文档属性
| 名称 | 湖北省武汉市外国语学校2024-2025学年八年级上学期10月月考数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 22:13:23 | ||
图片预览

文档简介
2024-2025武汉外校八(上)10月考数学试卷
一、选择题(每小题3分,共30分)
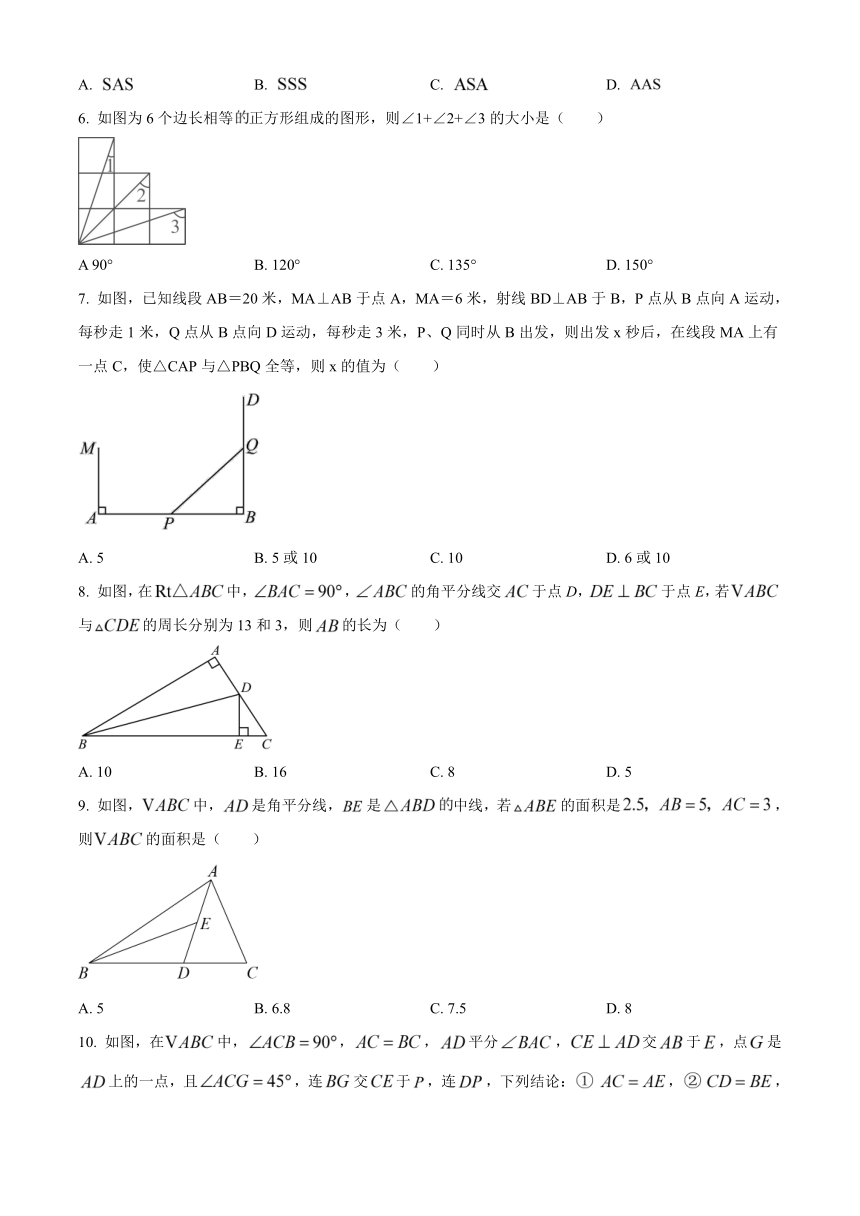
1. 如图,已知,,那么要得到,还应给出的条件是( )
A. B. C. D.
2. 小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带去( )
A. 第1块 B. 第2块 C. 第3块 D. 第4块
3. 已知,,面积为18平方厘米,则EF边上的高是( )
A. B. C. D.
4. 如图,在四边形中,,,,则的度数为( )
A. 145° B. 130° C. 110° D. 70°
5. 尺规作图中蕴含着丰富的数学知识和思想方法.如图,为了得到,在用直尺和圆规作图的过程中,得到的依据是( ).
A. B. C. D.
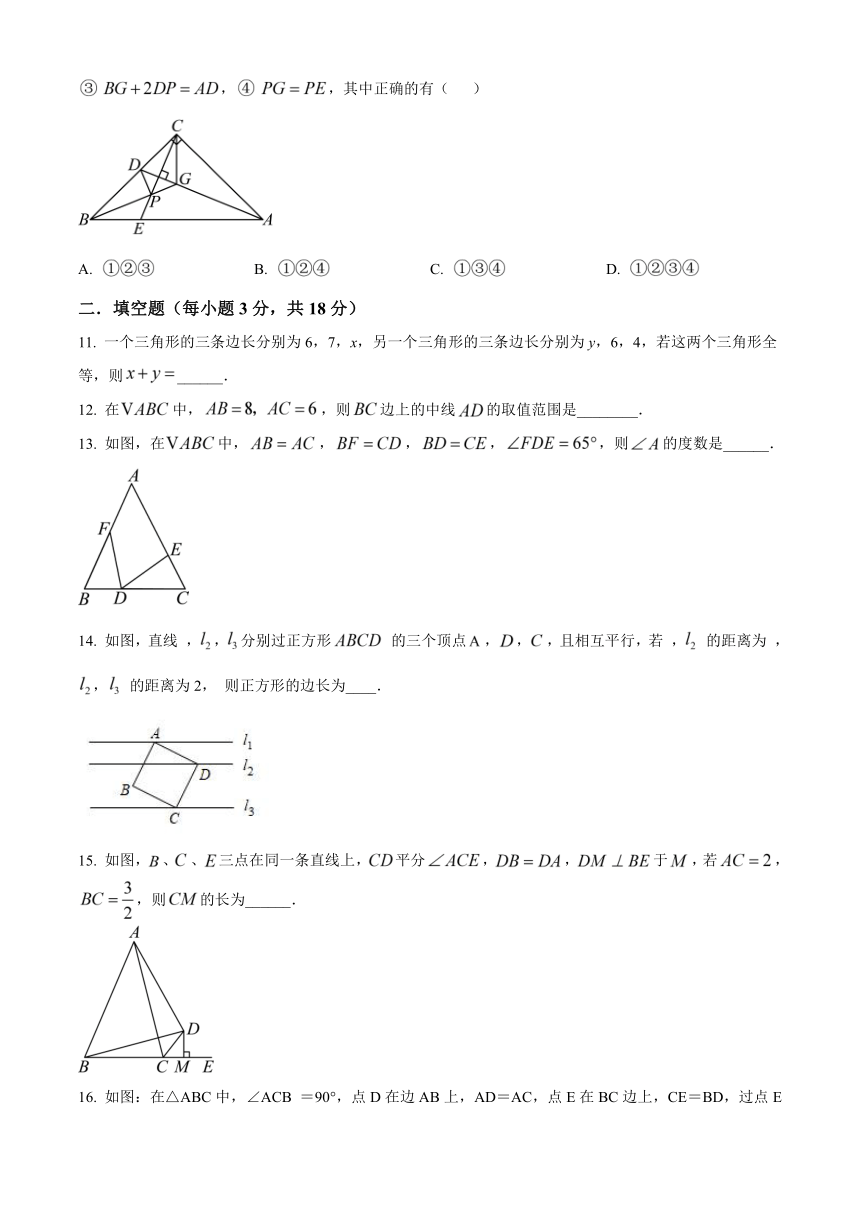
6. 如图为6个边长相等正方形组成的图形,则∠1+∠2+∠3的大小是( )
A 90° B. 120° C. 135° D. 150°
7. 如图,已知线段AB=20米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走3米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
A. 5 B. 5或10 C. 10 D. 6或10
8. 如图,在中,,的角平分线交于点D,于点E,若与的周长分别为13和3,则的长为( )
A. 10 B. 16 C. 8 D. 5
9. 如图,中,是角平分线,是中线,若的面积是,则的面积是( )
A. 5 B. 6.8 C. 7.5 D. 8
10. 如图,在中,,,平分,交于,点是上的一点,且,连交于,连,下列结论:,,,,其中正确的有( )
A. B. C. D.
二.填空题(每小题3分,共18分)
11. 一个三角形的三条边长分别为6,7,x,另一个三角形的三条边长分别为y,6,4,若这两个三角形全等,则______.
12. 在中,,则边上的中线的取值范围是________.
13. 如图,在中,,,,,则的度数是______.
14. 如图,直线 ,,分别过正方形 的三个顶点,,,且相互平行,若 , 的距离为 ,, 的距离为2, 则正方形的边长为____.
15. 如图,、、三点在同一条直线上,平分,,于,若,,则的长为______.
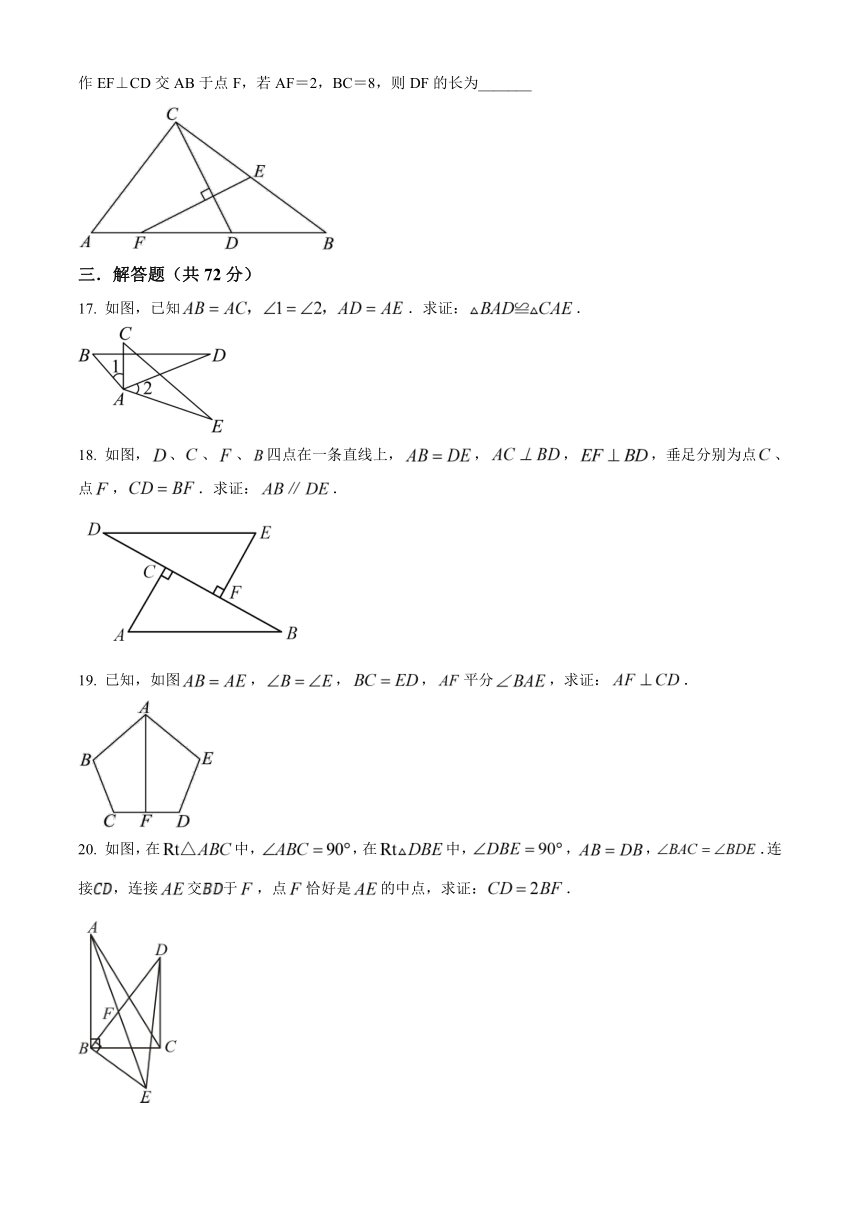
16. 如图:在△ABC中,∠ACB =90°,点D在边AB上,AD=AC,点E在BC边上,CE=BD,过点E作EF⊥CD交AB于点F,若AF=2,BC=8,则DF的长为_______
三.解答题(共72分)
17. 如图,已知.求证:.
18. 如图,、、、四点在一条直线上,,,,垂足分别为点、点,.求证:.
19. 已知,如图,,,平分,求证:.
20. 如图,在中,,在中,,,.连接,连接交于,点恰好是的中点,求证:.
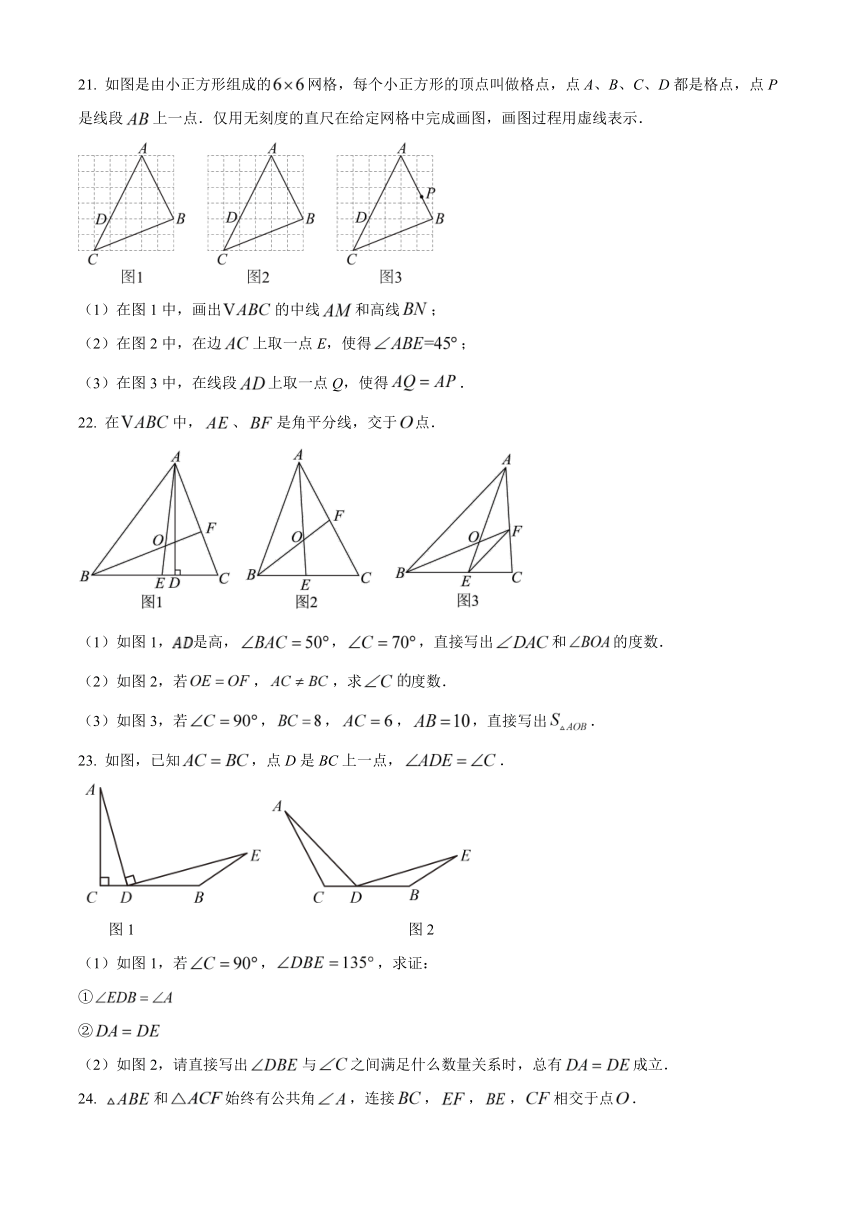
21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,点A、B、C、D都是格点,点P是线段上一点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)在图1中,画出的中线和高线;
(2)在图2中,在边上取一点E,使得;
(3)在图3中,在线段上取一点Q,使得.
22. 在中,、是角平分线,交于点.
(1)如图1,是高,,,直接写出和的度数.
(2)如图2,若,,求度数.
(3)如图3,若,,,,直接写出.
23. 如图,已知,点D是BC上一点,.
图1 图2
(1)如图1,若,,求证:
①
②
(2)如图2,请直接写出与之间满足什么数量关系时,总有成立.
24. 和始终有公共角,连接,,,相交于点.
(1)如图1,若,,求证:.
(2)如图2,若,且,求的度数(用含的式子表示)
(3)如图3,若,过点作且,连接并延长交于点,过点作于点,请直接写出与的关系为:_____________.
答案解析
一、选择题(每小题3分,共30分)
1. D.
2. D.
3. B.
4. C
5. .
6. C.
7. A.
8. D.
9. D.
10. .
二.填空题(每小题3分,共18分)
11. 11.
12.
13. ##度
14.
15.
16. 4
三.解答题(共72分)
17. 如图,已知.求证:.
证明:∵,
∴,即,
在和中,
,
∴.
18. 如图,、、、四点在一条直线上,,,,垂足分别为点、点,.求证:.
证明:,,
和为直角三角形,
,
,即,
在和中,
,
,
,
.
19. 已知,如图,,,平分,求证:.
证明:如图,连接,
∵,,
∴,
∴,
∵平分,
∴,
∴,即,
∴.
20. 如图,在中,,在中,,,.连接,连接交于,点恰好是的中点,求证:.
证明:如图,过A作于M,
∵,,,
∴,
∴,
∵,
∴,
∵F是的中点,
∴,
在和中,
∵,
∴,
∴,,
∴,,
∵,,
∴,
在和中,
,
∴,
∴,
∴.
21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,点A、B、C、D都是格点,点P是线段上一点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)在图1中,画出的中线和高线;
(2)在图2中,在边上取一点E,使得;
(3)在图3中,在线段上取一点Q,使得.
(1)解:,
,
为中点,即为中线;
由题意得:,,,
,
,
,
,
,
,
,即为高线;
中线和高线即为所求;
【小问2详解】
(2)如图,取格点Q,连接交于点E,
由题意得:,,,
,
,
,
,
,
,
,
点E即为所求点;
(3)【小问3详解】连接交格线于点,连接并延长交于点Q,
由题意得:垂直平分,,
,
,
,
,
,,
,
,
,
,
点即为所求点.
22. 在中,、是角平分线,交于点.
(1)如图1,是高,,,直接写出和的度数.
(2)如图2,若,,求的度数.
(3)如图3,若,,,,直接写出.
【答案】(1),
(2)
(3)10
解:(1)∵,
∴,
∵,
∴;
∵,,
∴,,
∵是的角平分线,
∴,
∴;
【小问2详解】
(2)解:连接,如图1,
∵、是角平分线,
∴是的角平分线,
∴,
过O作,,
则,
在与中,
,
∴,
∴,
∴,
∵、是角平分线,
∴,,
∵,
∴,
∴,
即,
∴;
【小问3详解】(3)如图2,连接,过O作于D,于G,于H,
∵、是角平分线,
∴,
∵,,,,
∴,
∴,
∴.
23. 如图,已知,点D是BC上一点,.
图1 图2
(1)如图1,若,,求证:
①
②
(2)如图2,请直接写出与之间满足什么数量关系时,总有成立.
(1)【小问1详解】证明:①∵,
∴
∴.
②在上截取,连接,
∵,
∴,
∴,
∵,
∴,即:,
由①知:,
∵,
∴,
∴.
(2)【小问2详解】当时,总有成立.理由如下:
如图,在上截取,连接,
∵,
∴,即:,
∵,,,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
24. 和始终有公共角,连接,,,相交于点.
(1)如图1,若,,求证:.
(2)如图2,若,且,求的度数(用含的式子表示)
(3)如图3,若,过点作且,连接并延长交于点,过点作于点,请直接写出与的关系为:_____________.
(1)【小问1详解】证明:在和中,
,
∴;
(2)【小问2详解】解:过点作于,作的延长线于,
∵,
∴,即
∵,,
∴,
在和中,
,
∴,
∴,
又∵,,
∴平分,
∴,
∵,,
∴,
∴的度数为;
(3)【小问3详解】与的关系为:.
理由如下:
连接,,,过点作于点,交的延长线于点,
∵,,
∴四边形为平行四边形,
∴,
∴,,
∴,
∵,,,
∴,
∵,,
∴平分,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴.
一、选择题(每小题3分,共30分)
1. 如图,已知,,那么要得到,还应给出的条件是( )
A. B. C. D.
2. 小明不慎将一块三角形的玻璃碎成如图所示的四块(图中所标1、2、3、4),你认为将其中的哪一块带去,就能配一块与原来大小一样的三角形玻璃?应该带去( )
A. 第1块 B. 第2块 C. 第3块 D. 第4块
3. 已知,,面积为18平方厘米,则EF边上的高是( )
A. B. C. D.
4. 如图,在四边形中,,,,则的度数为( )
A. 145° B. 130° C. 110° D. 70°
5. 尺规作图中蕴含着丰富的数学知识和思想方法.如图,为了得到,在用直尺和圆规作图的过程中,得到的依据是( ).
A. B. C. D.
6. 如图为6个边长相等正方形组成的图形,则∠1+∠2+∠3的大小是( )
A 90° B. 120° C. 135° D. 150°
7. 如图,已知线段AB=20米,MA⊥AB于点A,MA=6米,射线BD⊥AB于B,P点从B点向A运动,每秒走1米,Q点从B点向D运动,每秒走3米,P、Q同时从B出发,则出发x秒后,在线段MA上有一点C,使△CAP与△PBQ全等,则x的值为( )
A. 5 B. 5或10 C. 10 D. 6或10
8. 如图,在中,,的角平分线交于点D,于点E,若与的周长分别为13和3,则的长为( )
A. 10 B. 16 C. 8 D. 5
9. 如图,中,是角平分线,是中线,若的面积是,则的面积是( )
A. 5 B. 6.8 C. 7.5 D. 8
10. 如图,在中,,,平分,交于,点是上的一点,且,连交于,连,下列结论:,,,,其中正确的有( )
A. B. C. D.
二.填空题(每小题3分,共18分)
11. 一个三角形的三条边长分别为6,7,x,另一个三角形的三条边长分别为y,6,4,若这两个三角形全等,则______.
12. 在中,,则边上的中线的取值范围是________.
13. 如图,在中,,,,,则的度数是______.
14. 如图,直线 ,,分别过正方形 的三个顶点,,,且相互平行,若 , 的距离为 ,, 的距离为2, 则正方形的边长为____.
15. 如图,、、三点在同一条直线上,平分,,于,若,,则的长为______.
16. 如图:在△ABC中,∠ACB =90°,点D在边AB上,AD=AC,点E在BC边上,CE=BD,过点E作EF⊥CD交AB于点F,若AF=2,BC=8,则DF的长为_______
三.解答题(共72分)
17. 如图,已知.求证:.
18. 如图,、、、四点在一条直线上,,,,垂足分别为点、点,.求证:.
19. 已知,如图,,,平分,求证:.
20. 如图,在中,,在中,,,.连接,连接交于,点恰好是的中点,求证:.
21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,点A、B、C、D都是格点,点P是线段上一点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)在图1中,画出的中线和高线;
(2)在图2中,在边上取一点E,使得;
(3)在图3中,在线段上取一点Q,使得.
22. 在中,、是角平分线,交于点.
(1)如图1,是高,,,直接写出和的度数.
(2)如图2,若,,求度数.
(3)如图3,若,,,,直接写出.
23. 如图,已知,点D是BC上一点,.
图1 图2
(1)如图1,若,,求证:
①
②
(2)如图2,请直接写出与之间满足什么数量关系时,总有成立.
24. 和始终有公共角,连接,,,相交于点.
(1)如图1,若,,求证:.
(2)如图2,若,且,求的度数(用含的式子表示)
(3)如图3,若,过点作且,连接并延长交于点,过点作于点,请直接写出与的关系为:_____________.
答案解析
一、选择题(每小题3分,共30分)
1. D.
2. D.
3. B.
4. C
5. .
6. C.
7. A.
8. D.
9. D.
10. .
二.填空题(每小题3分,共18分)
11. 11.
12.
13. ##度
14.
15.
16. 4
三.解答题(共72分)
17. 如图,已知.求证:.
证明:∵,
∴,即,
在和中,
,
∴.
18. 如图,、、、四点在一条直线上,,,,垂足分别为点、点,.求证:.
证明:,,
和为直角三角形,
,
,即,
在和中,
,
,
,
.
19. 已知,如图,,,平分,求证:.
证明:如图,连接,
∵,,
∴,
∴,
∵平分,
∴,
∴,即,
∴.
20. 如图,在中,,在中,,,.连接,连接交于,点恰好是的中点,求证:.
证明:如图,过A作于M,
∵,,,
∴,
∴,
∵,
∴,
∵F是的中点,
∴,
在和中,
∵,
∴,
∴,,
∴,,
∵,,
∴,
在和中,
,
∴,
∴,
∴.
21. 如图是由小正方形组成的网格,每个小正方形的顶点叫做格点,点A、B、C、D都是格点,点P是线段上一点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)在图1中,画出的中线和高线;
(2)在图2中,在边上取一点E,使得;
(3)在图3中,在线段上取一点Q,使得.
(1)解:,
,
为中点,即为中线;
由题意得:,,,
,
,
,
,
,
,
,即为高线;
中线和高线即为所求;
【小问2详解】
(2)如图,取格点Q,连接交于点E,
由题意得:,,,
,
,
,
,
,
,
,
点E即为所求点;
(3)【小问3详解】连接交格线于点,连接并延长交于点Q,
由题意得:垂直平分,,
,
,
,
,
,,
,
,
,
,
点即为所求点.
22. 在中,、是角平分线,交于点.
(1)如图1,是高,,,直接写出和的度数.
(2)如图2,若,,求的度数.
(3)如图3,若,,,,直接写出.
【答案】(1),
(2)
(3)10
解:(1)∵,
∴,
∵,
∴;
∵,,
∴,,
∵是的角平分线,
∴,
∴;
【小问2详解】
(2)解:连接,如图1,
∵、是角平分线,
∴是的角平分线,
∴,
过O作,,
则,
在与中,
,
∴,
∴,
∴,
∵、是角平分线,
∴,,
∵,
∴,
∴,
即,
∴;
【小问3详解】(3)如图2,连接,过O作于D,于G,于H,
∵、是角平分线,
∴,
∵,,,,
∴,
∴,
∴.
23. 如图,已知,点D是BC上一点,.
图1 图2
(1)如图1,若,,求证:
①
②
(2)如图2,请直接写出与之间满足什么数量关系时,总有成立.
(1)【小问1详解】证明:①∵,
∴
∴.
②在上截取,连接,
∵,
∴,
∴,
∵,
∴,即:,
由①知:,
∵,
∴,
∴.
(2)【小问2详解】当时,总有成立.理由如下:
如图,在上截取,连接,
∵,
∴,即:,
∵,,,
∴,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴.
24. 和始终有公共角,连接,,,相交于点.
(1)如图1,若,,求证:.
(2)如图2,若,且,求的度数(用含的式子表示)
(3)如图3,若,过点作且,连接并延长交于点,过点作于点,请直接写出与的关系为:_____________.
(1)【小问1详解】证明:在和中,
,
∴;
(2)【小问2详解】解:过点作于,作的延长线于,
∵,
∴,即
∵,,
∴,
在和中,
,
∴,
∴,
又∵,,
∴平分,
∴,
∵,,
∴,
∴的度数为;
(3)【小问3详解】与的关系为:.
理由如下:
连接,,,过点作于点,交的延长线于点,
∵,,
∴四边形为平行四边形,
∴,
∴,,
∴,
∵,,,
∴,
∵,,
∴平分,
∴,
∵,
∴,
∴,
∴,
∵,
∴,
∴,
∵,
∴.
同课章节目录
