2024-2025学年广东省广州市华南师大附中高三(上)月考数学试卷(一)(含答案)
文档属性
| 名称 | 2024-2025学年广东省广州市华南师大附中高三(上)月考数学试卷(一)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 242.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 09:32:39 | ||
图片预览




文档简介
2024-2025学年广东省华南师大附中高三(上)月考数学试卷(一)
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.半径为的圆上长度为的圆弧所对的圆心角是( )
A. B. C. D.
2.直线过抛物线的焦点,且在轴与轴上的截距相同,则的方程是( )
A. B. C. D.
3.已知,,则( )
A. B.
C. D.
4.函数的图象不可能是( )
A. B.
C. D.
5.已知,,满足,,,则( )
A. B. C. D.
6.若正数满足,则的最小值是( )
A. B. C. D.
7.已知,设甲:,乙:,则( )
A. 甲是乙的充分条件但不是必要条件
B. 甲是乙的必要条件但不是充分条件
C. 甲是乙的充要条件
D. 甲既不是乙的充分条件也不是乙的必要条件
8.已知正实数,,满足,,,则,,的大小关系是( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知函数,则( )
A. 有两个极值点 B. 有一个零点
C. 点是曲线的对称中心 D. 直线是曲线的切线
10.已知函数的定义域为,且,,为偶函数,则( )
A. B. 为奇函数 C. D.
11.已知函数,曲线过不在上的点恰能作两条的切线,切点分别为,,则( )
A. B. C. D.
三、填空题:本题共3小题,每小题5分,共15分。
12.某中学的、两个班级有相同的语文、数学、英语教师,现对此个班级某天上午的节课进行排课,节语文课,节数学课,节英语课,要求每个班级的节语文课连在一起,节数学课连在一起,则共有 种不同的排课方式用数字作答
13.已知函数为定义在上的奇函数,则 ______.
14.一段路上有个路灯,,,一开始它们都是关着的,有名行人先后经过这段路,对每个,当第名行人经过时,他将所有下标为的倍数的路灯,,的开关状态改变问当第名行人经过后,有______个路灯处于开着的状态.
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
记的内角,,所对的边分别为,,,已知.
求;
若,,求的面积.
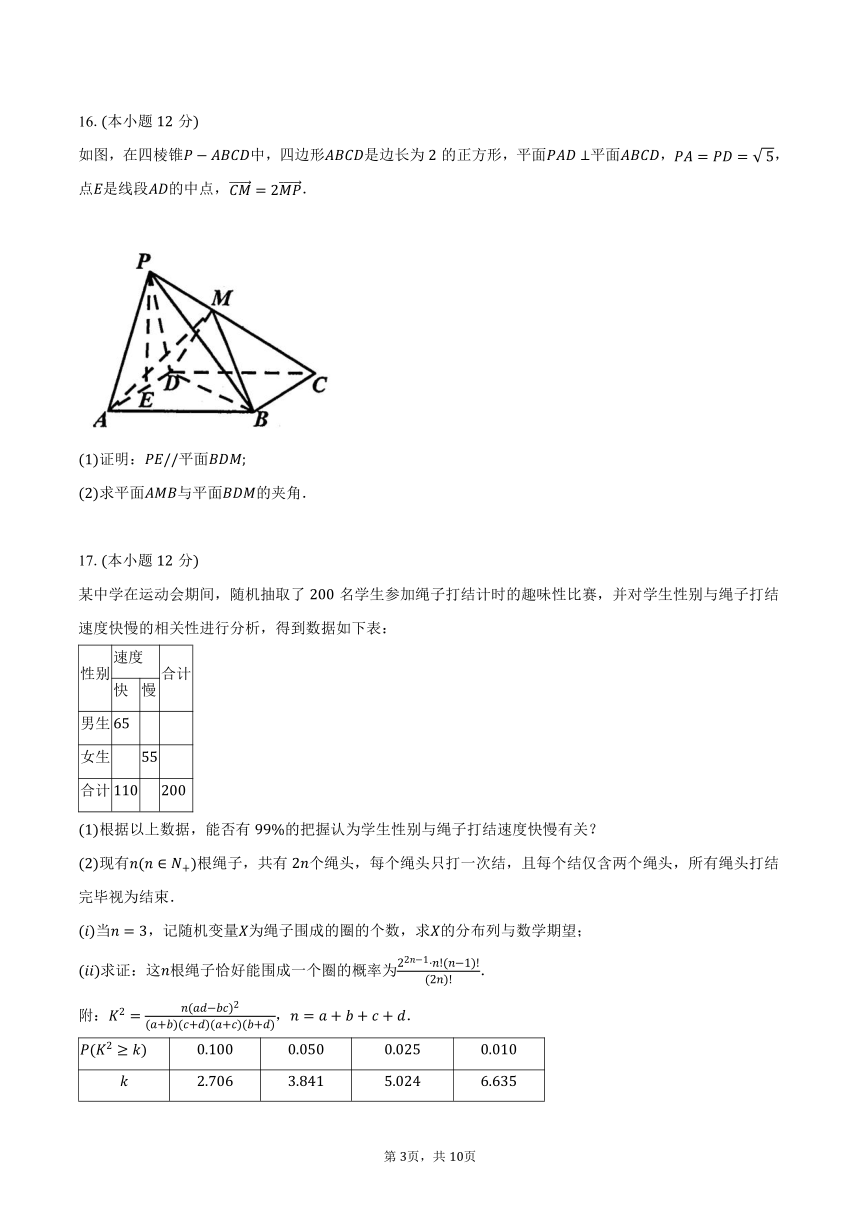
16.本小题分
如图,在四棱锥中,四边形是边长为的正方形,平面平面,,点是线段的中点,.
证明:平面
求平面与平面的夹角.
17.本小题分
某中学在运动会期间,随机抽取了名学生参加绳子打结计时的趣味性比赛,并对学生性别与绳子打结速度快慢的相关性进行分析,得到数据如下表:
性别 速度 合计
快 慢
男生
女生
合计
根据以上数据,能否有的把握认为学生性别与绳子打结速度快慢有关?
现有根绳子,共有个绳头,每个绳头只打一次结,且每个结仅含两个绳头,所有绳头打结完毕视为结束.
当,记随机变量为绳子围成的圈的个数,求的分布列与数学期望;
求证:这根绳子恰好能围成一个圈的概率为.
附:,.
18.本小题分
费马原理,也称为时间最短原理:光传播的路径是光程取极值的路径在凸透镜成像中,根据费马原理可以推出光线经凸透镜至像点的总光程为定值光程为光在某介质中传播的路程与该介质折射率的乘积一般而言,空气的折射率约为如图是折射率为的某平凸透镜的纵截面图,其中平凸透镜的平面圆直径为,且与轴交于点平行于轴的平行光束从左向右照向该平凸透镜,所有光线经折射后全部汇聚在点处并在此成像提示:光线从平凸透镜的平面进入时不发生折射
设该平凸透镜纵截面中的曲线为曲线,试判断属于哪一种圆锥曲线,并求出其相应的解析式.
设曲线为解析式同的完整圆锥曲线,直线与交于,两点,交轴于点,交轴于点点不与的顶点重合若,,试求出点所有可能的坐标.
19.本小题分
已知函数.
Ⅰ当时,记函数的导数为,求的值.
Ⅱ当,时,证明:
Ⅲ当时,令,的图象在,处切线的斜率相同,记的最小值为,求的最小值.
注:是自然对数的底数
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:由题可得
,所以或
因为,
可得,
又因为,
得,
是三角形内角,所以,
所以得,
所以只可能是,,此时,所以,,
所以,
所以.
16.解:连接交于,由是的中点可得,
则与相似,所以,
又,所以,
又平面,平面
所以平面
,点是线段的中点,
,
又平面平面,平面平面,平面,
平面,
如图,建立空间直角坐标系,,,,,,,
,,
则,
设平面的法向量为,
由,,
则可得,
同理可得平面的法向量为,
所以,,
所以平面与平面的夹角为
17.解:补全列联表如下:
别 速度 合计
快 慢
男生
女生
合计
则,
所以有的把握,认为学生性别与绳子打结速度快慢有关;
易知的所有可能取值为,,,
此时,,,
则的分布列为:
所以;
证明:不妨令绳头编号为,,,,,,
可以与绳头打结形成一个圆的绳头除了,外还有种可能,
假设绳头与绳头打结,
那么相当于对剩下根绳子进行打结,
不妨设根绳子打结后可成圆的种数为,
那么经过一次打结后,剩下根绳子打结后可成圆的种数为,
所以,,
即,
,
,,
,
以上各式累乘得,
易知,
所以,
另一方面,对个绳头进行任意个绳头打结,
总共有,
则.
18.解:设上任意一点,,光线从点至点的光程为,
光线穿过凸透镜后从点折射到点的光程为,
则,,
由题意得,则,化简得,
所以,所以.
令,得,
所以为双曲线的一部分,解析式为.
由题意知.
设,,,,
则,,,
因为,所以,,
由题意知,,得,,
即,.
将点的坐标代入,得,
化简整理得.
同理可得,
所以与为方程的两个解,
所以.
由题知,所以,解得,
所以点的坐标可能为或.
19.解:Ⅰ当时,,
Ⅱ当,时,,,
令,
,
所以在上单调递增,
所以,
则,,,
在上单调递增,
,得证.
Ⅲ当时,,
,
所以在上单调递增,,上单调递减,
由题意,得到,
,
由得到,记,
则,
,
在上单调递减,在上单调递增.
,
即,
当时,,
令,
,
所以在上单调递增,
所以,即,
所以在上单调递增,
所以
即的最小值为
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.半径为的圆上长度为的圆弧所对的圆心角是( )
A. B. C. D.
2.直线过抛物线的焦点,且在轴与轴上的截距相同,则的方程是( )
A. B. C. D.
3.已知,,则( )
A. B.
C. D.
4.函数的图象不可能是( )
A. B.
C. D.
5.已知,,满足,,,则( )
A. B. C. D.
6.若正数满足,则的最小值是( )
A. B. C. D.
7.已知,设甲:,乙:,则( )
A. 甲是乙的充分条件但不是必要条件
B. 甲是乙的必要条件但不是充分条件
C. 甲是乙的充要条件
D. 甲既不是乙的充分条件也不是乙的必要条件
8.已知正实数,,满足,,,则,,的大小关系是( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.已知函数,则( )
A. 有两个极值点 B. 有一个零点
C. 点是曲线的对称中心 D. 直线是曲线的切线
10.已知函数的定义域为,且,,为偶函数,则( )
A. B. 为奇函数 C. D.
11.已知函数,曲线过不在上的点恰能作两条的切线,切点分别为,,则( )
A. B. C. D.
三、填空题:本题共3小题,每小题5分,共15分。
12.某中学的、两个班级有相同的语文、数学、英语教师,现对此个班级某天上午的节课进行排课,节语文课,节数学课,节英语课,要求每个班级的节语文课连在一起,节数学课连在一起,则共有 种不同的排课方式用数字作答
13.已知函数为定义在上的奇函数,则 ______.
14.一段路上有个路灯,,,一开始它们都是关着的,有名行人先后经过这段路,对每个,当第名行人经过时,他将所有下标为的倍数的路灯,,的开关状态改变问当第名行人经过后,有______个路灯处于开着的状态.
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
记的内角,,所对的边分别为,,,已知.
求;
若,,求的面积.
16.本小题分
如图,在四棱锥中,四边形是边长为的正方形,平面平面,,点是线段的中点,.
证明:平面
求平面与平面的夹角.
17.本小题分
某中学在运动会期间,随机抽取了名学生参加绳子打结计时的趣味性比赛,并对学生性别与绳子打结速度快慢的相关性进行分析,得到数据如下表:
性别 速度 合计
快 慢
男生
女生
合计
根据以上数据,能否有的把握认为学生性别与绳子打结速度快慢有关?
现有根绳子,共有个绳头,每个绳头只打一次结,且每个结仅含两个绳头,所有绳头打结完毕视为结束.
当,记随机变量为绳子围成的圈的个数,求的分布列与数学期望;
求证:这根绳子恰好能围成一个圈的概率为.
附:,.
18.本小题分
费马原理,也称为时间最短原理:光传播的路径是光程取极值的路径在凸透镜成像中,根据费马原理可以推出光线经凸透镜至像点的总光程为定值光程为光在某介质中传播的路程与该介质折射率的乘积一般而言,空气的折射率约为如图是折射率为的某平凸透镜的纵截面图,其中平凸透镜的平面圆直径为,且与轴交于点平行于轴的平行光束从左向右照向该平凸透镜,所有光线经折射后全部汇聚在点处并在此成像提示:光线从平凸透镜的平面进入时不发生折射
设该平凸透镜纵截面中的曲线为曲线,试判断属于哪一种圆锥曲线,并求出其相应的解析式.
设曲线为解析式同的完整圆锥曲线,直线与交于,两点,交轴于点,交轴于点点不与的顶点重合若,,试求出点所有可能的坐标.
19.本小题分
已知函数.
Ⅰ当时,记函数的导数为,求的值.
Ⅱ当,时,证明:
Ⅲ当时,令,的图象在,处切线的斜率相同,记的最小值为,求的最小值.
注:是自然对数的底数
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:由题可得
,所以或
因为,
可得,
又因为,
得,
是三角形内角,所以,
所以得,
所以只可能是,,此时,所以,,
所以,
所以.
16.解:连接交于,由是的中点可得,
则与相似,所以,
又,所以,
又平面,平面
所以平面
,点是线段的中点,
,
又平面平面,平面平面,平面,
平面,
如图,建立空间直角坐标系,,,,,,,
,,
则,
设平面的法向量为,
由,,
则可得,
同理可得平面的法向量为,
所以,,
所以平面与平面的夹角为
17.解:补全列联表如下:
别 速度 合计
快 慢
男生
女生
合计
则,
所以有的把握,认为学生性别与绳子打结速度快慢有关;
易知的所有可能取值为,,,
此时,,,
则的分布列为:
所以;
证明:不妨令绳头编号为,,,,,,
可以与绳头打结形成一个圆的绳头除了,外还有种可能,
假设绳头与绳头打结,
那么相当于对剩下根绳子进行打结,
不妨设根绳子打结后可成圆的种数为,
那么经过一次打结后,剩下根绳子打结后可成圆的种数为,
所以,,
即,
,
,,
,
以上各式累乘得,
易知,
所以,
另一方面,对个绳头进行任意个绳头打结,
总共有,
则.
18.解:设上任意一点,,光线从点至点的光程为,
光线穿过凸透镜后从点折射到点的光程为,
则,,
由题意得,则,化简得,
所以,所以.
令,得,
所以为双曲线的一部分,解析式为.
由题意知.
设,,,,
则,,,
因为,所以,,
由题意知,,得,,
即,.
将点的坐标代入,得,
化简整理得.
同理可得,
所以与为方程的两个解,
所以.
由题知,所以,解得,
所以点的坐标可能为或.
19.解:Ⅰ当时,,
Ⅱ当,时,,,
令,
,
所以在上单调递增,
所以,
则,,,
在上单调递增,
,得证.
Ⅲ当时,,
,
所以在上单调递增,,上单调递减,
由题意,得到,
,
由得到,记,
则,
,
在上单调递减,在上单调递增.
,
即,
当时,,
令,
,
所以在上单调递增,
所以,即,
所以在上单调递增,
所以
即的最小值为
第1页,共1页
同课章节目录
