苏教版六年级上册数学1长方体和正方体的体积之水中浸物 课件(共21张PPT)
文档属性
| 名称 | 苏教版六年级上册数学1长方体和正方体的体积之水中浸物 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 18.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
长方体和正方体的体积
之
水中浸物
追本溯源
复习
1.长方体的长、宽、高分别为5、2、4,则体积为
2.长方体的体积为100,长、宽分别为5、2,则高为
3.长方体的底面积为20,高为5,则体积为
V长方体=长×宽×高
V正方体=棱长3
V长方体=底面积×高
三种情况
①完全浸没
②部分浸没/不完全浸没
③溢出
完全浸没
开心一刻
探索一
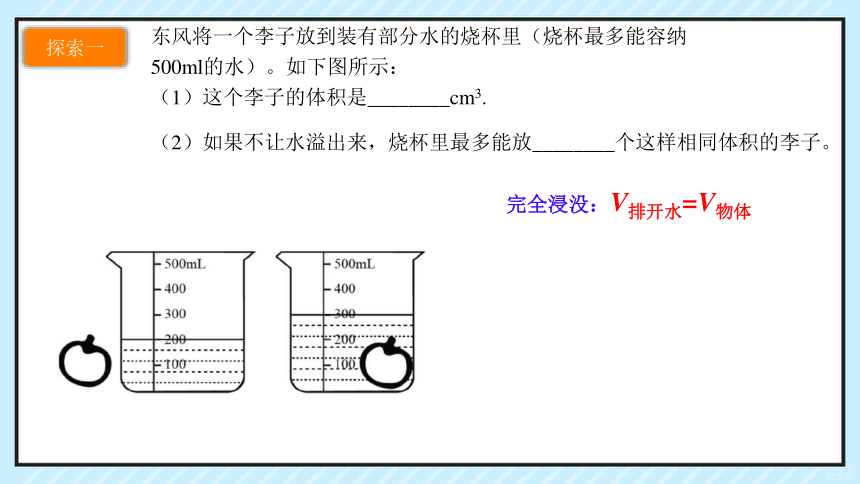
东风将一个李子放到装有部分水的烧杯里(烧杯最多能容纳500ml的水)。如下图所示:
(1)这个李子的体积是________cm3.
(2)如果不让水溢出来,烧杯里最多能放________个这样相同体积的李子。
完全浸没:V排开水=V物体
例题1
一个长方体水箱,长14cm ,宽10cm ,高16cm ,水箱里有10cm深的水(如左图).贝贝将一块石头放入水中后,水面比原来上升了2.5cm (如右图).(水箱的厚度忽略不计)
(1)石块的体积是________立方厘米.
V长方体=底面积×高
例题1
一个长方体水箱,长14cm ,宽10cm ,高16cm ,水箱里有10cm深的水(如左图).贝贝将一块石头放入水中后,水面比原来上升了2.5cm (如右图).(水箱的厚度忽略不计)
(2)如果再放入1块相同大小的石头,水面高度是________厘米.
例题1
一个长方体水箱,长14cm ,宽10cm ,高16cm ,水箱里有10cm深的水(如左图).贝贝将一块石头放入水中后,水面比原来上升了2.5cm (如右图).(水箱的厚度忽略不计)
(3)如果在(2)的基础上再放入1块相同大小的石头,水面高度是________厘米.
若水面高度>容器高度,则溢出
实际高度=容器高度
练习
董小亮老师完全浸泡在自己豪华的泳池底,进行闭气练习,接着他上岸了. 水位下降了0.05米,已知这个私人泳池底面积为80平方米,你能算出董小亮老师的体积吗?
完全浸没:V排开水=V物体
例题2
长、宽、高分别为8cm、12cm、20cm的长方体玻璃容器中放入一个棱长6cm的立方体铁块,再将容器灌满水.此时若将铁块取出,水面高度是________厘米.
挑战
在一个长、宽、高分别为6厘米、5厘米、15厘米的长方体容器中,有一个铁块完全漫没在水中,当铁块从容器中取出时,容器中的水面高度下降了4厘米;
若将这个铁块完全浸没在另一个长、宽、高分别为8厘米、2厘米、20厘米的长方体容器中(水不会溢出),水面将上升________厘米.
部分浸没
探索二
如图,一个长、宽、高分别为7、8、17的长方体,在竖直方向挖掉了一个底面积为6的长方体的洞(洞上下打穿),那么这个中空的长方体的体积是多少?
从底面看
从上面看
加油7
一只装有水的长方体玻璃杯,底面积是80平方厘米,杯高是15厘米,水深10厘米.现将一个底面积是16平方厘米,高为20厘米的长方体铁块竖直放在水中后.现在水面高度是_______厘米
①水的体积不变
②水仍是柱体→“回形”柱体
例题4
如图,一个长、宽、高分别为20厘米、15厘米、12厘米的长方体容器,存高一半的水,现在有一块棱长为10厘米的正方体铁块放入水中,水面高度变为________厘米.
不确定时先假设,一般假设完全浸没
溢出
溢出
思维导图
长方体和正方体的体积
之
水中浸物
追本溯源
复习
1.长方体的长、宽、高分别为5、2、4,则体积为
2.长方体的体积为100,长、宽分别为5、2,则高为
3.长方体的底面积为20,高为5,则体积为
V长方体=长×宽×高
V正方体=棱长3
V长方体=底面积×高
三种情况
①完全浸没
②部分浸没/不完全浸没
③溢出
完全浸没
开心一刻
探索一
东风将一个李子放到装有部分水的烧杯里(烧杯最多能容纳500ml的水)。如下图所示:
(1)这个李子的体积是________cm3.
(2)如果不让水溢出来,烧杯里最多能放________个这样相同体积的李子。
完全浸没:V排开水=V物体
例题1
一个长方体水箱,长14cm ,宽10cm ,高16cm ,水箱里有10cm深的水(如左图).贝贝将一块石头放入水中后,水面比原来上升了2.5cm (如右图).(水箱的厚度忽略不计)
(1)石块的体积是________立方厘米.
V长方体=底面积×高
例题1
一个长方体水箱,长14cm ,宽10cm ,高16cm ,水箱里有10cm深的水(如左图).贝贝将一块石头放入水中后,水面比原来上升了2.5cm (如右图).(水箱的厚度忽略不计)
(2)如果再放入1块相同大小的石头,水面高度是________厘米.
例题1
一个长方体水箱,长14cm ,宽10cm ,高16cm ,水箱里有10cm深的水(如左图).贝贝将一块石头放入水中后,水面比原来上升了2.5cm (如右图).(水箱的厚度忽略不计)
(3)如果在(2)的基础上再放入1块相同大小的石头,水面高度是________厘米.
若水面高度>容器高度,则溢出
实际高度=容器高度
练习
董小亮老师完全浸泡在自己豪华的泳池底,进行闭气练习,接着他上岸了. 水位下降了0.05米,已知这个私人泳池底面积为80平方米,你能算出董小亮老师的体积吗?
完全浸没:V排开水=V物体
例题2
长、宽、高分别为8cm、12cm、20cm的长方体玻璃容器中放入一个棱长6cm的立方体铁块,再将容器灌满水.此时若将铁块取出,水面高度是________厘米.
挑战
在一个长、宽、高分别为6厘米、5厘米、15厘米的长方体容器中,有一个铁块完全漫没在水中,当铁块从容器中取出时,容器中的水面高度下降了4厘米;
若将这个铁块完全浸没在另一个长、宽、高分别为8厘米、2厘米、20厘米的长方体容器中(水不会溢出),水面将上升________厘米.
部分浸没
探索二
如图,一个长、宽、高分别为7、8、17的长方体,在竖直方向挖掉了一个底面积为6的长方体的洞(洞上下打穿),那么这个中空的长方体的体积是多少?
从底面看
从上面看
加油7
一只装有水的长方体玻璃杯,底面积是80平方厘米,杯高是15厘米,水深10厘米.现将一个底面积是16平方厘米,高为20厘米的长方体铁块竖直放在水中后.现在水面高度是_______厘米
①水的体积不变
②水仍是柱体→“回形”柱体
例题4
如图,一个长、宽、高分别为20厘米、15厘米、12厘米的长方体容器,存高一半的水,现在有一块棱长为10厘米的正方体铁块放入水中,水面高度变为________厘米.
不确定时先假设,一般假设完全浸没
溢出
溢出
思维导图
