2024-2025学年上海市松江一中高二(上)段考数学试卷(一)(含答案)
文档属性
| 名称 | 2024-2025学年上海市松江一中高二(上)段考数学试卷(一)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 102.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 10:04:17 | ||
图片预览



文档简介
2024-2025学年上海市松江一中高二(上)段考数学试卷(一)
一、单选题:本题共4小题,共18分。在每小题给出的选项中,只有一项是符合题目要求的。
1.过平面外一点,可以作这个平面的平行线的条数是( )
A. 条 B. 条 C. 超过条但有限 D. 无数条
2.已知,是异面直线,,是两个不同的平面,且,,则下列说法正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
3.如图,两个共底面的正四棱锥底面是正方形,顶点、与正方形的中心的连线与底面垂直组成一个八面体,且该八面体的各棱长均相等,则( )
A. 异面直线与所成的角为
B.
C. 平面平面
D. 直线与平面所成的角为
4.从正方体八个顶点的两两连线中任取两条直线,,且,是异面直线,则,所成角的余弦值的所有可能取值构成的集合是( )
A. B.
C. D.
二、填空题:本题共12小题,共54分。
5.二面角的平面角的取值范围是______.
6.若直线平行于平面内的直线,则与的位置关系是______.
7.若空间中有两条直线,则“这两条直线为异面直线”是“这两条直线没有公共点”的______条件.
8.已知复数满足为虚数单位,则 ______.
9.已知数列的前项和 ______.
10.如图所示直角梯形上下两底分别为和,高为,则利用斜二测画法所得其直观图的面积为______.
11.已知正方形所在的平面,且,,则和平面所成角的大小为______.
12.在空间四边形中,,,,分别是边,,,的中点,若四边形对角线,
对角线与所成的角为,则 ______.
13.正方体的棱长为,,分别为、的中点,则平面截正方体所得的截面面积为______.
14.如图,正方体的棱长为,,分别为,的中点,是底面上一点若平面,则与平面成角的正弦值的取值范围是______.
15.如图,在直三棱柱中,底面为直角三角形,,,,是上一动点,则的最小值是______.
16.刻画空间的弯曲性是几何研究的重要内容,在数学上用曲率刻画空间弯曲性规定:多面体的顶点的曲率等于与多面体在该点的面角之和的差多面体的面的内角叫做多面体的面角,角度用弧度制,多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和例如:正四面体四个面都是等边三角形围成的几何体在每个顶点有个面角,每个面角是,所以正四面体在每个顶点的曲率为,故其总曲率为我们把平面四边形外的点连接顶点、、、构成的几何体称为四棱锥,根据曲率的定义,四棱锥的总曲率为______.
三、解答题:本题共5小题,共78分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知长方体中,、分别为和的中点,求证:
,,,四点共面;
、、三线共点.
18.本小题分
在空间四边形中,,分别为,的中点,若,求异面直线和所成的角;
如图,长方体中,,求异面直线与所成的角.
19.本小题分
一山坡的倾斜度山坡面与水平面所成二面角的度数是,斜坡上一直道,它和坡脚成,为解决山腰处居民的饮水问题,有甲、乙两种方案.
方案甲:一次性投资万元打深水井,取用与坡脚水平的暗河中的水经检验符合饮用水标准;
方案乙:沿铺设自来水管道,第一个费用为万元,以后每往上一个所需费用比前一个的费用扩大倍;
如果处高出暗河,那么选用哪个方案比较合理?请你说明理由不考虑其他因素
20.本小题分
如图,在直角梯形中,,,,底面且.
求证:是直角三角形;
在上取点,交平面于,求证:四边形为直角梯形;
若,写出的表达式并求当为何值时,最小?最小值是多少?
21.本小题分
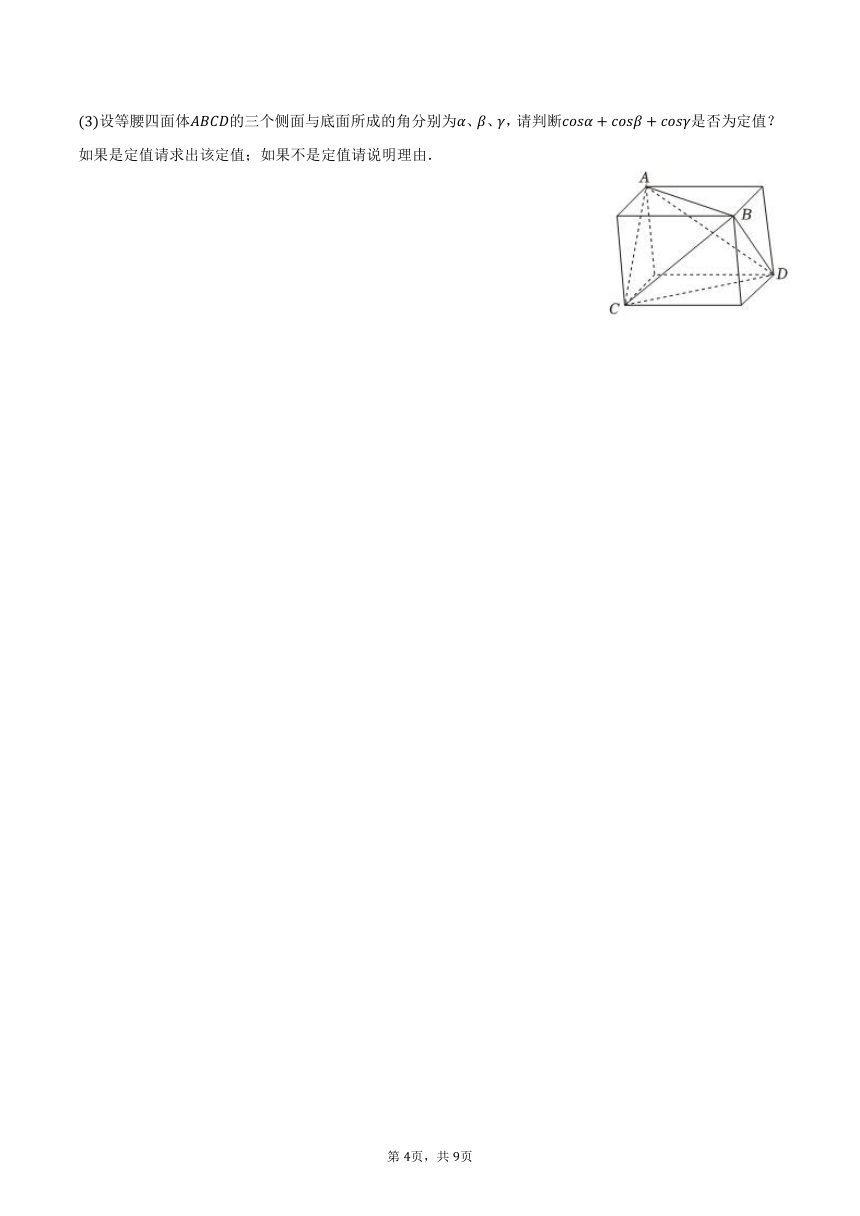
定义:对棱相等的四面体为等腰四面体等腰四面体可以由长方体切割产生,如图.
在等腰四面体中,有几对棱长相等?请分别写出这几对相等的棱长;
求证:等腰四面体每个面的三角形均为锐角三角形;
设等腰四面体的三个侧面与底面所成的角分别为、、,请判断是否为定值?如果是定值请求出该定值;如果不是定值请说明理由.
参考答案
1.
2.
3.
4.
5.
6.或
7.充分不必要
8.
9.
10.
11.
12.或
13.
14.
15.
16.
17.证明:如图,连接,
因为、分别为和的中点,
所以,
因为在长方体中,
易知,,
所以四边形为平行四边形,
所以,所以,
所以与确定一个平面,
所以,,,四点共面;
因为,且,
所以直线与必相交,
设,
因为,平面,
所以平面,
又因为,平面,
所以平面,
所以是平面与平面的公共点,
又因为平面平面,所以,
所以、、三线共点.
18.解:如图所示,取的中点,连接,,
因为,分别是,的中点,所以且,且,
所以或其补角即为异面直线与所成的角,
又,所以.
在中,由余弦定理可得:,
所以异面直线与所成的角的余弦值为.
故异面直线和所成的角为.
如图连接,,
在长方体中,因为,
所以直线与所成角等于与所成的角,
在中,,.,
由余弦定理可得,,
则异面直线与所成的角.
19.解:如图所示,是坡面,是直道,设.
设是点到水平面的垂线,垂足,作且交于,连结,
则根据三垂线定理可得,
坡面和水平面所成的二面角的平面角即为,
又根据题意可得,
所以,所以;
方案乙:铺自来水管道所需费用,万元,,万元,
,万元,,万元,
总共需要费用万元万元,
故选用方案甲比较合算.
20.证明:,即,
平面,平面,,
由,且,都在平面内,
平面,平面,可得,
即都是直角三角形;
证明:底面,平面,直角梯形中,,
,,且,,平面,
可得平面,平面,可得,
,,且,,平面,
可得平面,平面,可得,
又,故平面,平面,则,
在四边形中,,又,,
四边形为直角梯形.
解:在中,,,,
根据余弦定理,
在中,,,,
,
对于二次函数,当时,取得最小值,
此时.
21.解:由等腰四面体的定义可知,
在等腰四面体中,共有对棱长相等的对棱,
分别是,,;
证明:如图,长宽高分别为、、的长方体的六条面对角线组成等腰四面体,
四个面是全等的三角形,
三边长分别为,,,
不妨设,则最大边所对角的余弦值为:
,为锐角,
三角形为锐角三角形,
等腰四面体每个面的三角形均为锐角三角形;
如图,长宽高分别为、、的长方体的六条面对角线组成等腰四面体,
以为原点,所在直线为轴,所在直线为轴,所在直线为轴,建立空间直角坐标系,
则,,,,
,,,
,,
设平面的一个法向量为,
则有,取,得,
设平面的一个法向量为,
则有,取,得,
设平面的一个法向量为,
则有,取,得,
设平面的一个法向量为,
则有,取,得,
设等腰四面体的三个侧面,,与底面所成的角分别为、、,
则
,
故为定值.
第1页,共1页
一、单选题:本题共4小题,共18分。在每小题给出的选项中,只有一项是符合题目要求的。
1.过平面外一点,可以作这个平面的平行线的条数是( )
A. 条 B. 条 C. 超过条但有限 D. 无数条
2.已知,是异面直线,,是两个不同的平面,且,,则下列说法正确的是( )
A. 若,则 B. 若,则
C. 若,则 D. 若,则
3.如图,两个共底面的正四棱锥底面是正方形,顶点、与正方形的中心的连线与底面垂直组成一个八面体,且该八面体的各棱长均相等,则( )
A. 异面直线与所成的角为
B.
C. 平面平面
D. 直线与平面所成的角为
4.从正方体八个顶点的两两连线中任取两条直线,,且,是异面直线,则,所成角的余弦值的所有可能取值构成的集合是( )
A. B.
C. D.
二、填空题:本题共12小题,共54分。
5.二面角的平面角的取值范围是______.
6.若直线平行于平面内的直线,则与的位置关系是______.
7.若空间中有两条直线,则“这两条直线为异面直线”是“这两条直线没有公共点”的______条件.
8.已知复数满足为虚数单位,则 ______.
9.已知数列的前项和 ______.
10.如图所示直角梯形上下两底分别为和,高为,则利用斜二测画法所得其直观图的面积为______.
11.已知正方形所在的平面,且,,则和平面所成角的大小为______.
12.在空间四边形中,,,,分别是边,,,的中点,若四边形对角线,
对角线与所成的角为,则 ______.
13.正方体的棱长为,,分别为、的中点,则平面截正方体所得的截面面积为______.
14.如图,正方体的棱长为,,分别为,的中点,是底面上一点若平面,则与平面成角的正弦值的取值范围是______.
15.如图,在直三棱柱中,底面为直角三角形,,,,是上一动点,则的最小值是______.
16.刻画空间的弯曲性是几何研究的重要内容,在数学上用曲率刻画空间弯曲性规定:多面体的顶点的曲率等于与多面体在该点的面角之和的差多面体的面的内角叫做多面体的面角,角度用弧度制,多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和例如:正四面体四个面都是等边三角形围成的几何体在每个顶点有个面角,每个面角是,所以正四面体在每个顶点的曲率为,故其总曲率为我们把平面四边形外的点连接顶点、、、构成的几何体称为四棱锥,根据曲率的定义,四棱锥的总曲率为______.
三、解答题:本题共5小题,共78分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知长方体中,、分别为和的中点,求证:
,,,四点共面;
、、三线共点.
18.本小题分
在空间四边形中,,分别为,的中点,若,求异面直线和所成的角;
如图,长方体中,,求异面直线与所成的角.
19.本小题分
一山坡的倾斜度山坡面与水平面所成二面角的度数是,斜坡上一直道,它和坡脚成,为解决山腰处居民的饮水问题,有甲、乙两种方案.
方案甲:一次性投资万元打深水井,取用与坡脚水平的暗河中的水经检验符合饮用水标准;
方案乙:沿铺设自来水管道,第一个费用为万元,以后每往上一个所需费用比前一个的费用扩大倍;
如果处高出暗河,那么选用哪个方案比较合理?请你说明理由不考虑其他因素
20.本小题分
如图,在直角梯形中,,,,底面且.
求证:是直角三角形;
在上取点,交平面于,求证:四边形为直角梯形;
若,写出的表达式并求当为何值时,最小?最小值是多少?
21.本小题分
定义:对棱相等的四面体为等腰四面体等腰四面体可以由长方体切割产生,如图.
在等腰四面体中,有几对棱长相等?请分别写出这几对相等的棱长;
求证:等腰四面体每个面的三角形均为锐角三角形;
设等腰四面体的三个侧面与底面所成的角分别为、、,请判断是否为定值?如果是定值请求出该定值;如果不是定值请说明理由.
参考答案
1.
2.
3.
4.
5.
6.或
7.充分不必要
8.
9.
10.
11.
12.或
13.
14.
15.
16.
17.证明:如图,连接,
因为、分别为和的中点,
所以,
因为在长方体中,
易知,,
所以四边形为平行四边形,
所以,所以,
所以与确定一个平面,
所以,,,四点共面;
因为,且,
所以直线与必相交,
设,
因为,平面,
所以平面,
又因为,平面,
所以平面,
所以是平面与平面的公共点,
又因为平面平面,所以,
所以、、三线共点.
18.解:如图所示,取的中点,连接,,
因为,分别是,的中点,所以且,且,
所以或其补角即为异面直线与所成的角,
又,所以.
在中,由余弦定理可得:,
所以异面直线与所成的角的余弦值为.
故异面直线和所成的角为.
如图连接,,
在长方体中,因为,
所以直线与所成角等于与所成的角,
在中,,.,
由余弦定理可得,,
则异面直线与所成的角.
19.解:如图所示,是坡面,是直道,设.
设是点到水平面的垂线,垂足,作且交于,连结,
则根据三垂线定理可得,
坡面和水平面所成的二面角的平面角即为,
又根据题意可得,
所以,所以;
方案乙:铺自来水管道所需费用,万元,,万元,
,万元,,万元,
总共需要费用万元万元,
故选用方案甲比较合算.
20.证明:,即,
平面,平面,,
由,且,都在平面内,
平面,平面,可得,
即都是直角三角形;
证明:底面,平面,直角梯形中,,
,,且,,平面,
可得平面,平面,可得,
,,且,,平面,
可得平面,平面,可得,
又,故平面,平面,则,
在四边形中,,又,,
四边形为直角梯形.
解:在中,,,,
根据余弦定理,
在中,,,,
,
对于二次函数,当时,取得最小值,
此时.
21.解:由等腰四面体的定义可知,
在等腰四面体中,共有对棱长相等的对棱,
分别是,,;
证明:如图,长宽高分别为、、的长方体的六条面对角线组成等腰四面体,
四个面是全等的三角形,
三边长分别为,,,
不妨设,则最大边所对角的余弦值为:
,为锐角,
三角形为锐角三角形,
等腰四面体每个面的三角形均为锐角三角形;
如图,长宽高分别为、、的长方体的六条面对角线组成等腰四面体,
以为原点,所在直线为轴,所在直线为轴,所在直线为轴,建立空间直角坐标系,
则,,,,
,,,
,,
设平面的一个法向量为,
则有,取,得,
设平面的一个法向量为,
则有,取,得,
设平面的一个法向量为,
则有,取,得,
设平面的一个法向量为,
则有,取,得,
设等腰四面体的三个侧面,,与底面所成的角分别为、、,
则
,
故为定值.
第1页,共1页
同课章节目录
