圆（第二课时）

课件25张PPT。一切平面图形中，最美的是圆！
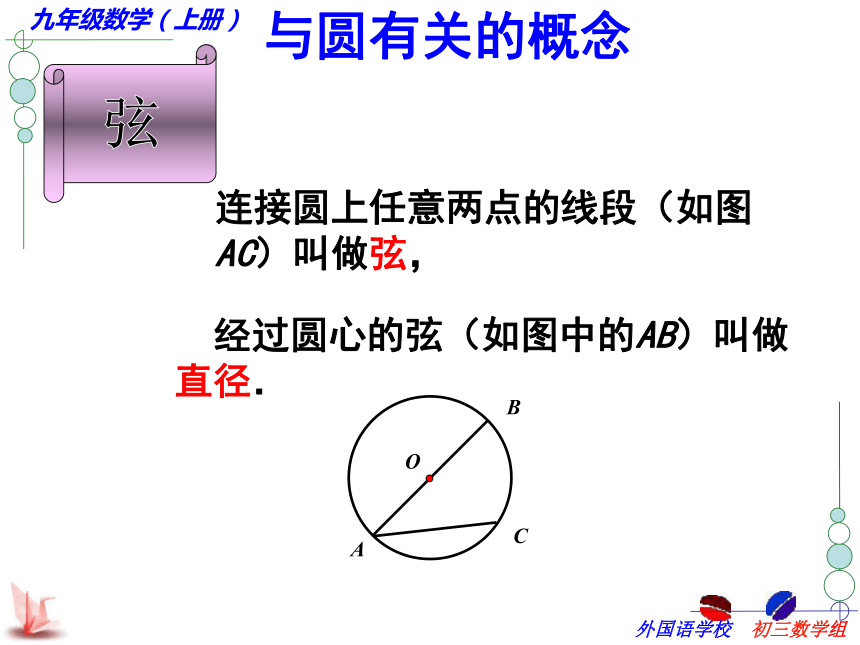
——毕达哥拉斯[古希腊数学家5.1圆的有关概念 经过圆心的弦（如图中的AB）叫做直径．·COAB连接圆上任意两点的线段（如图AC）叫做弦，与圆有关的概念CBOAFEDM 问：
（1）FC是弦吗？为什么？
（2）CM是弦吗？为什么？
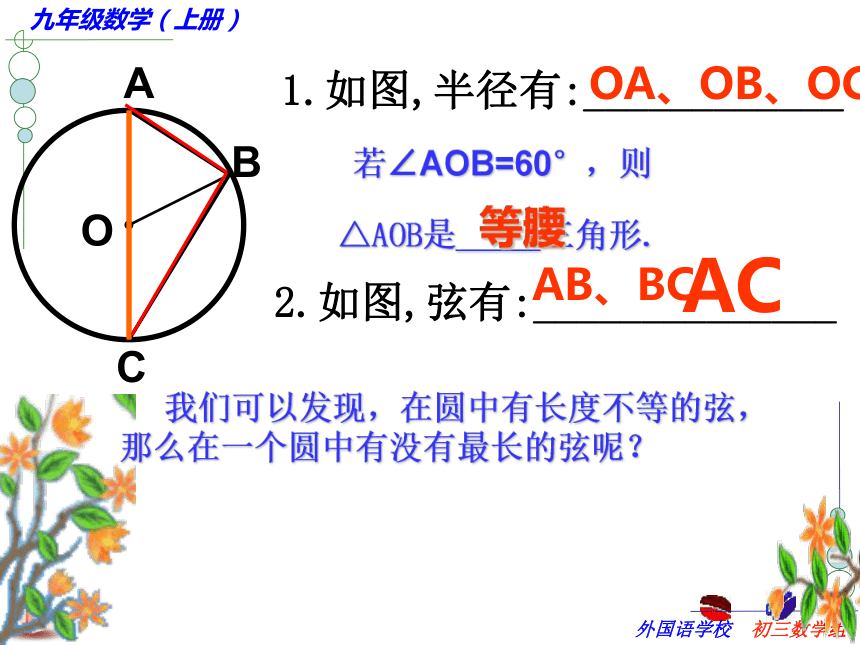
（3）从图中你能找到哪些弦？●OBCA 1.如图,半径有:____________OA、OB、OC
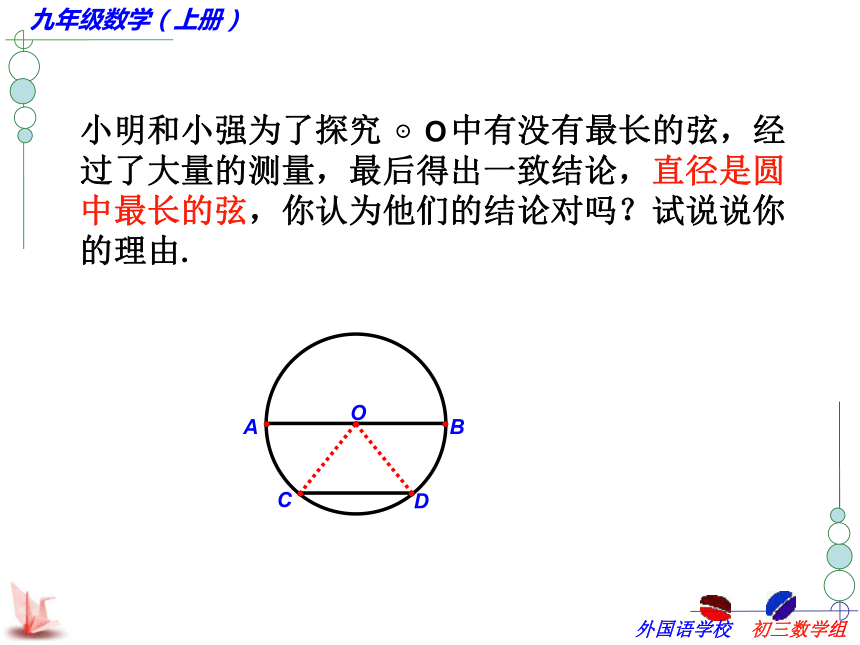
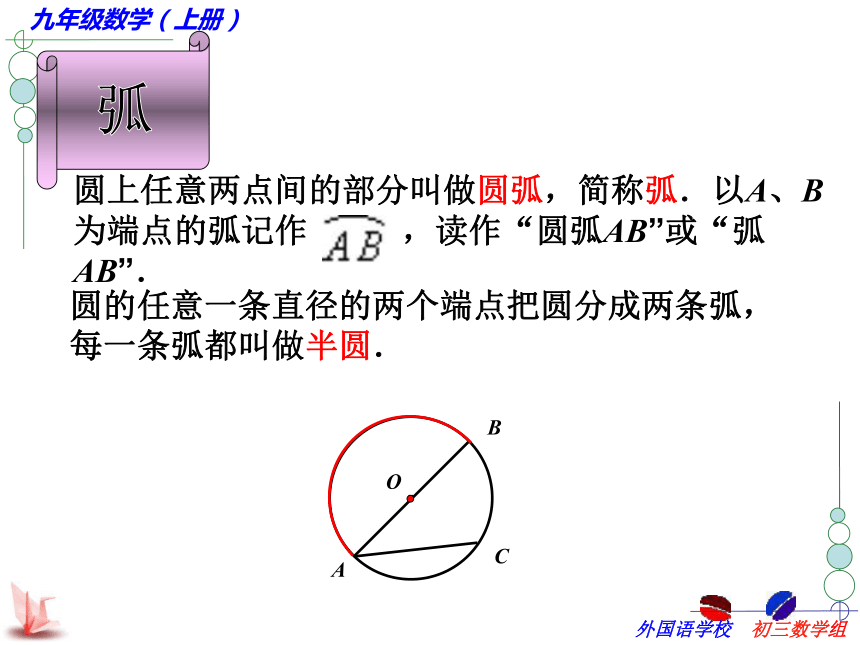
△AOB是_____三角形. 2.如图,弦有:______________AB、BCAC 我们可以发现，在圆中有长度不等的弦，那么在一个圆中有没有最长的弦呢？等边等腰若∠AOB=60°，则圆的任意一条直径的两个端点把圆分成两条弧，每一条弧都叫做半圆．·COAB圆上任意两点间的部分叫做圆弧，简称弧．以A、B为端点的弧记作 ，读作“圆弧AB”或“弧AB”．·COAB小于半圆的弧（如图中的　　　　）叫做劣弧；大于半圆的弧（用三个字母表示，如图中的 ）叫做优弧.●OBCA 1.如图,弧有:______________2 .劣弧有：优弧有：六条如图，请正确的方式表示出以点A为端点的优弧及劣弧. 弦与弧1、请写出图中所有的弦；2、请任选一条弦，写出这条弦所对的弧；一条弦对的弧有两条圆心角定义：顶点在圆心的角叫做圆心角　　　　　　　　　　　　　　ＡＯＢＣ找出⊙Ｏ中的圆心角：∠ＡＯＣ　　 ∠ＢＯＣ思考：∠ＡＢＣ是不是圆心角？同心圆 等圆同圆或等圆的半径相等。
在同圆或等圆中，能够互相重合的弧叫等弧。圆心相同，半径不同半径相同，能够互相重合的圆在大小不等的两个圆中，不存在等弧 1、抢答:(判断正误?)(1)弦是直径；(2)半圆是弧，但弧不一定是半圆；(5)圆心相同，半径相等的两个圆是同心圆;(6)半径相等的两个圆是等圆.(3)半圆是最长的弧；(4)直径是最长的弦；课堂大比武：(7)若P是⊙O内一点，过P点的最长的弦有一条。2、下列说法错误的是（ ）A、圆上的点到圆心的距离相等
B、过圆心的线段是直径
C、直径是圆中最长的弦
D、半径相等的圆是等圆
3、下列说法：①直径是弦 ②弦是直径 ③半圆是弧，但弧不一定是半圆 ④长度相等的两条弧是等弧⑤完全重合的两条弧是等弧。
正确的命题有（ ）
A、1个 B、2个 C、3个 D、4个BC4、你见过树木的年轮吗?从树木的年轮,可以很清楚的看出树木生长的年龄,如果一棵20年树龄的红杉树的树干直径是23cm,这棵红杉树的半径每年增加多少?.解:
23÷2÷20=0.575（cm ）答: 这棵红衫树的半径每年增加0.575cm 5、如图：AB,CD为⊙O的直径，DE∥AB, ∠EOD=100°,求∠AOC的度数。6、如图，E是⊙O上一点，AB是⊙O的弦，OE的延长线交AB的延长线于C。如果BC=OE， ∠C=40°，求∠ EOA的度数。7、如图：CD为⊙O直径，AE交⊙O于B，且AB=OC，∠A=200,求∠DOE的度数.变化：如图：CD为⊙O直径，AE交⊙O于B，且AB=OC，求证∠DOE=3 ∠A8、已知:如图,点O是∠EPF的平分线的一点,以O为圆心的圆和EPF的两边分别交于点A、B和C、D. 求证: ∠OBA=∠OCD9、如图：以O为圆心的同心圆，大圆的弦AB交小圆于C,D两点。
求证:(1)AC=BD;(2) ∠AOC=∠BOD.E某部队在灯塔A的周围进行爆破作业，A的周围3km内的水域为危险区域，有一渔船误入离A点2km的B处，为了尽快驶离危险区域，该般应沿什么方向航行？提示：
1、理解题意，画出图形；2、结合图形，分析题意。你能用数学知识来解释原因吗？CD对于平面图形A,如果存在一个圆,使图形A上的任意一点到圆心的距离不大于这个圆的半径,那么称图形A被这个圆所覆盖.例如,图中的三角形被一个圆所覆盖.
回答问题:1、边长为1cm的正方形被一个半径为r的圆所覆盖, r的最小值是多少?
2、边长为1cm的正三角形被一个半径为r的圆所覆盖, r的最小值是多少?
3、半径为1cm 的圆被边长为a的正方形所覆盖, a的最小值是多少?
4、半径为1cm的圆被边长为a的正三角形所覆盖, a的最小值是多少?想一想：
本节课你有什么收获？
有什么困惑？谢谢！