圆的对称性（第二课时）

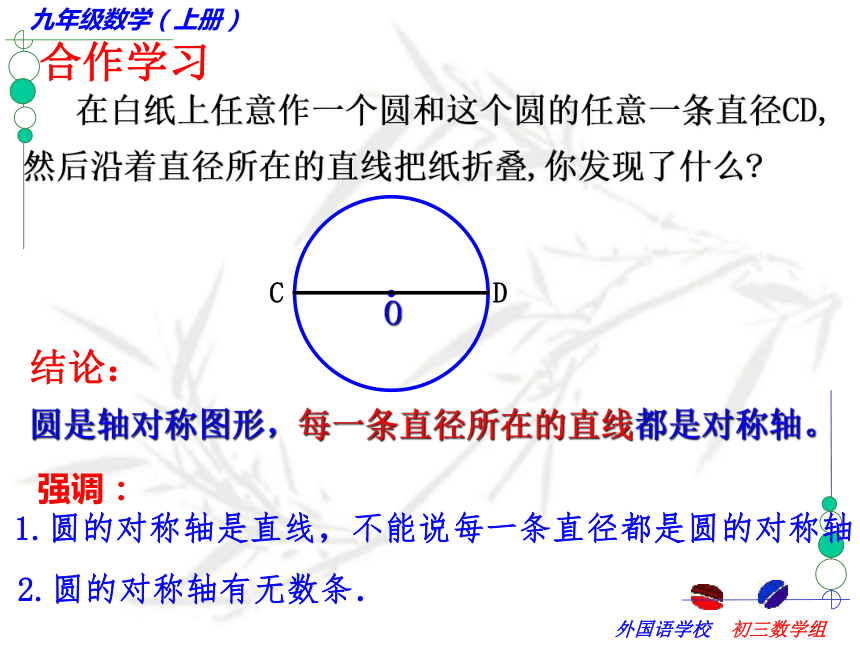
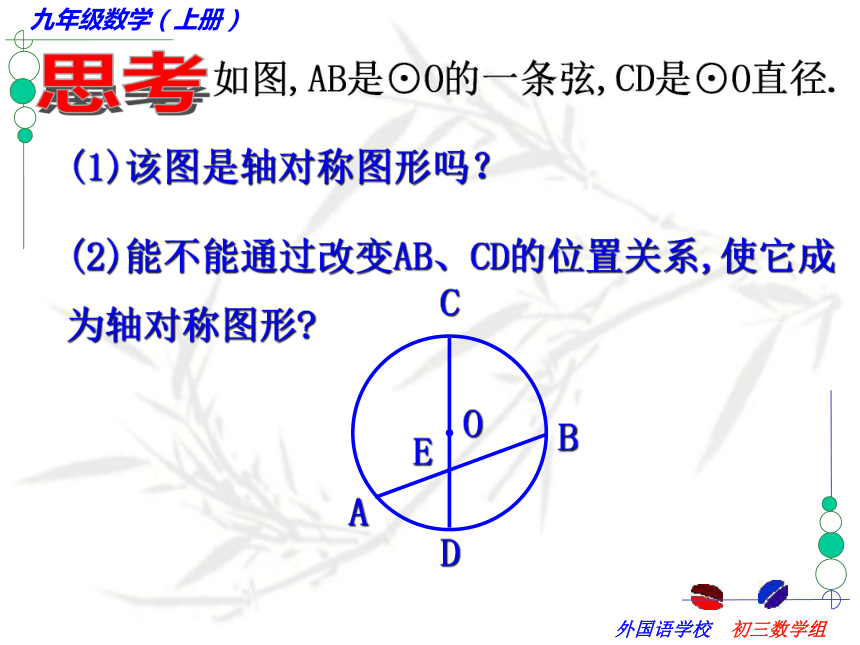
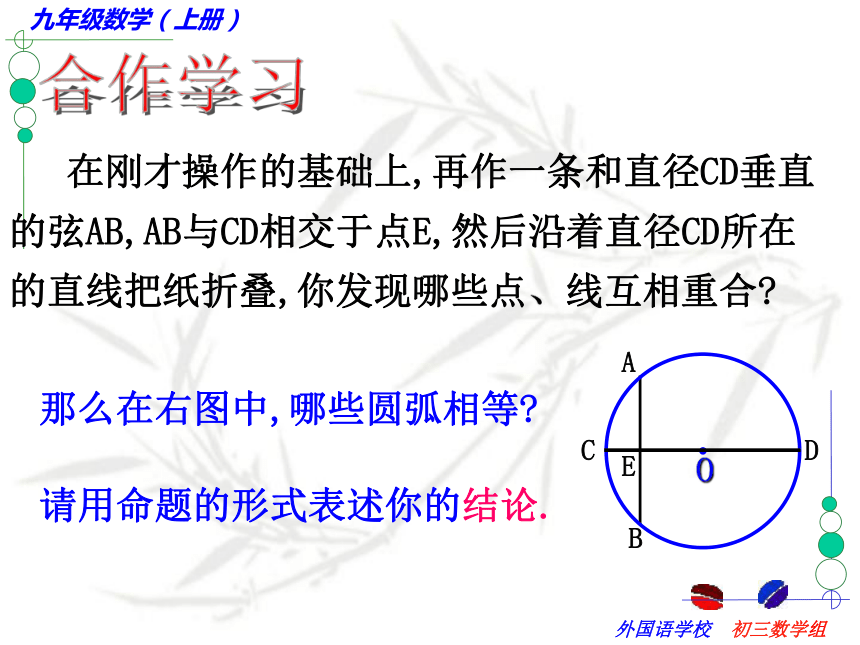
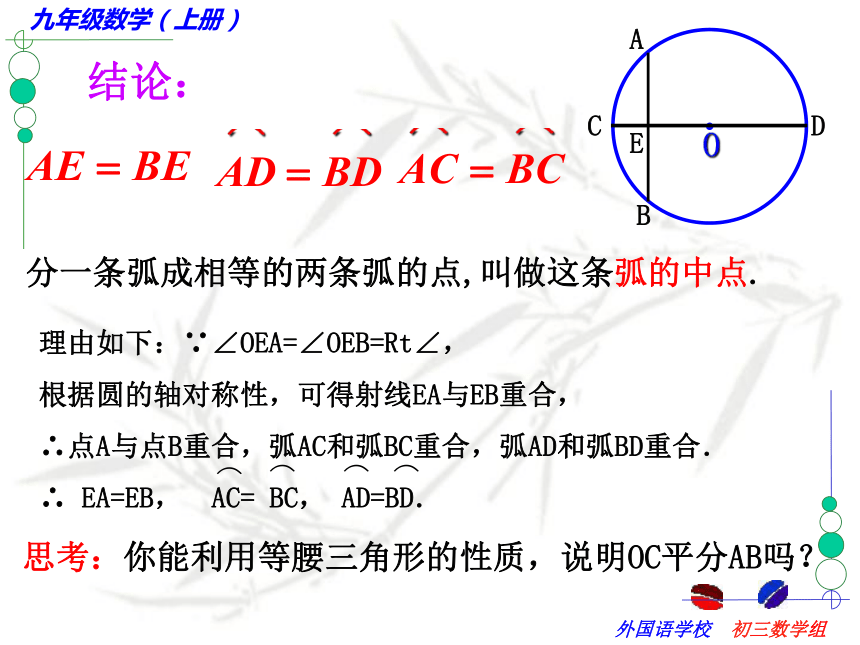
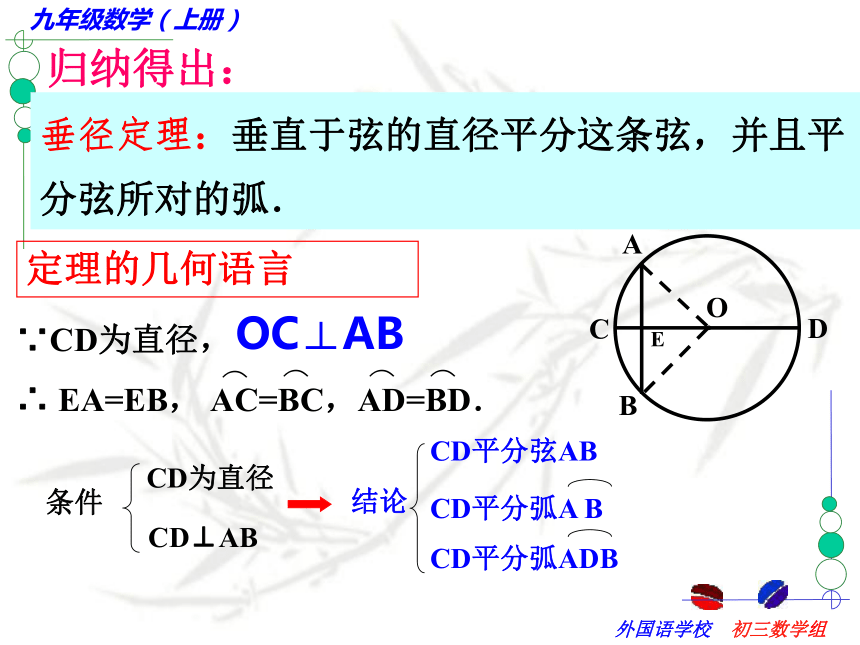
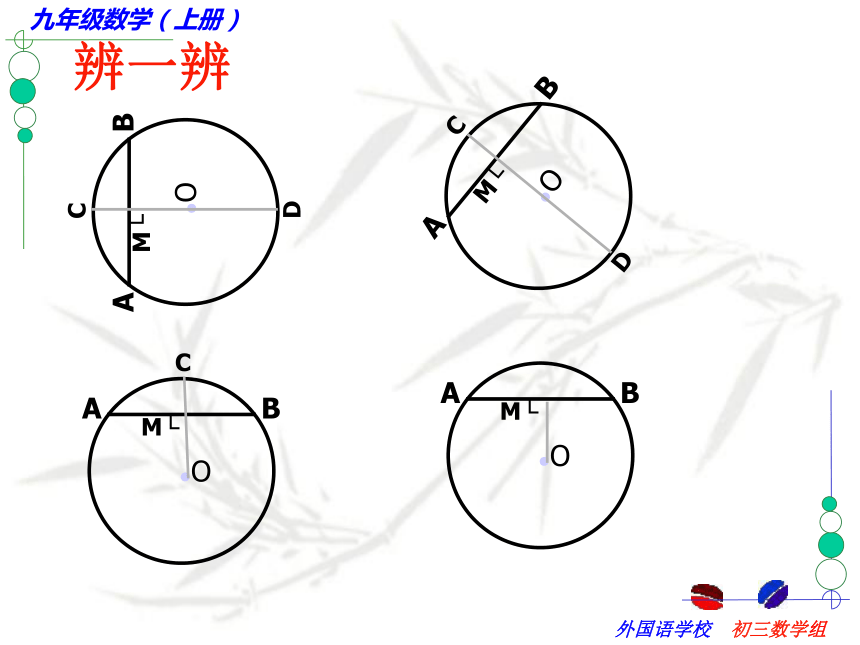
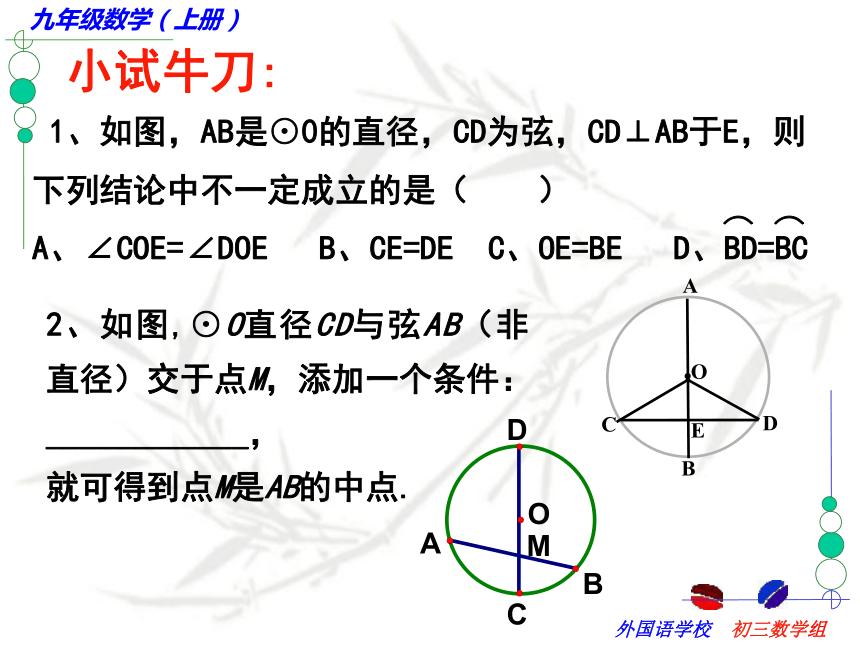
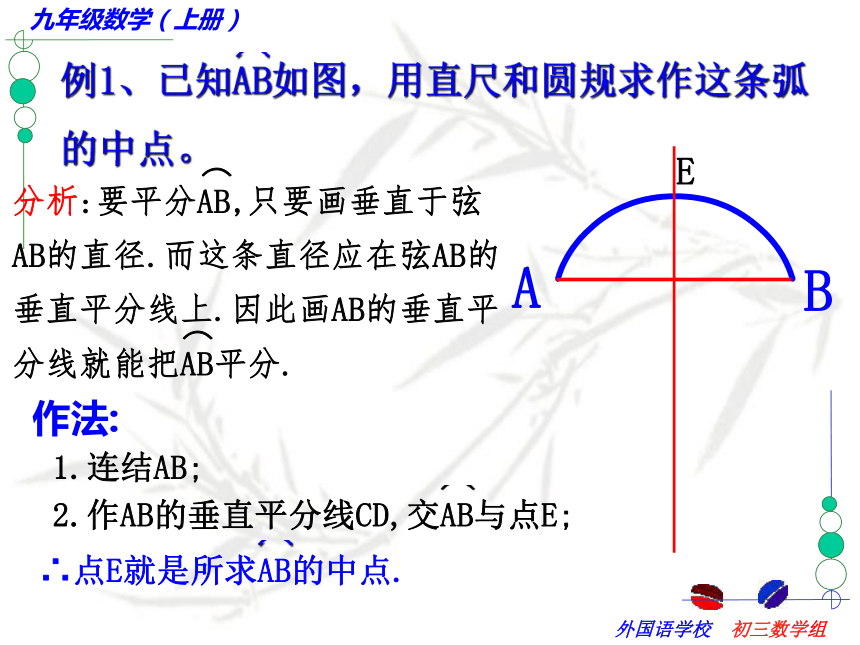
课件37张PPT。第五章 圆（二）请观察下列三个银行标志有何共同点? 在白纸上任意作一个圆和这个圆的任意一条直径CD, 然后沿着直径所在的直线把纸折叠,你发现了什么?结论： 圆是轴对称图形，每一条直径所在的直线都是对称轴。强调：1.圆的对称轴是直线，不能说每一条直径都是圆的对称轴2.圆的对称轴有无数条．合作学习(1)该图是轴对称图形吗？(2)能不能通过改变AB、CD的位置关系,使它成为轴对称图形?合作学习 在刚才操作的基础上,再作一条和直径CD垂直的弦AB,AB与CD相交于点E,然后沿着直径CD所在的直线把纸折叠,你发现哪些点、线互相重合?那么在右图中,哪些圆弧相等?请用命题的形式表述你的结论.思考：你能利用等腰三角形的性质，说明OC平分AB吗？结论：分一条弧成相等的两条弧的点,叫做这条弧的中点.归纳得出：垂径定理：垂直于弦的直径平分这条弦，并且平分弦所对的弧．定理的几何语言OC⊥AB辨一辨小试牛刀:2、如图,⊙O直径CD与弦AB（非直径）交于点M，添加一个条件：____________，
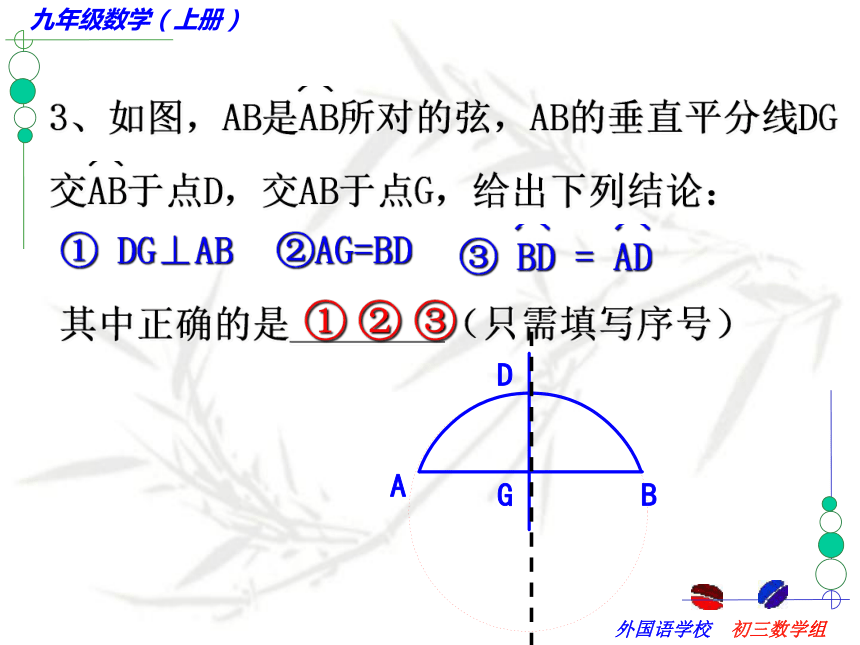
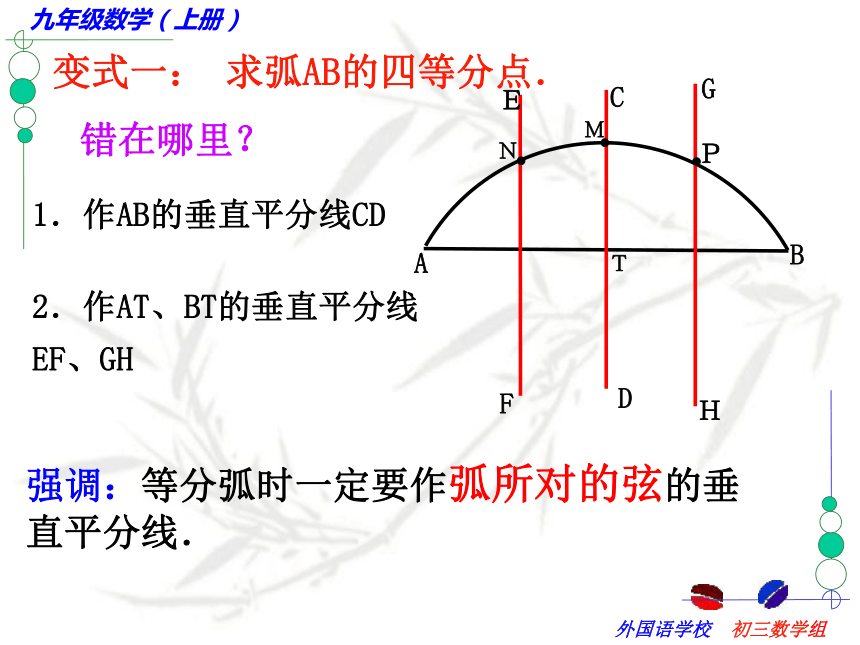
就可得到点M是AB的中点.②AG=BD其中正确的是________（只需填写序号）① ② ③E1.连结AB;作法:CDABＭFG错在哪里？1．作AB的垂直平分线CD2．作AT、BT的垂直平分线EF、GHＴＥＮＨＰ强调：等分弧时一定要作弧所对的弦的垂直平分线．变式一： 求弧AB的四等分点．变式一： 求弧AB的四等分点．CDABEFGmn变式二：你能确定弧AB所在圆的圆心吗？OABC ab方法：只要在圆弧上任意取三点，连结两条弦，画这两条弦的垂直平分线，交点即为圆弧所在圆的圆心．画一画 1、如图,M为⊙O内的一点,利用尺规作一条弦AB,使AB过点M.并且使AM=BM.你能画过点M最长的弦呢?你还能画过点M最短的弦呢?2、过已知⊙O内的一点A作弦,使A是该弦的中点,
然后作出弦所对的两条弧的中点BC就是所要求的弦；点D、E就是所要求的弦所对的两条弧的中点中点；画一画例2、如图，一条排水管的截面。已知排水管的半径OB=10，水面宽AB=16。求截面圆心O到水面的距离。DC1088解:作OC⊥AB于C,由定理得:
AC=BC=1/2AB=0.5×16=8
由勾股定理得:圆心到圆的一条弦的距离叫做弦心距如上图中的OC的长就是弦AB的弦心距答:截面圆心O到水面的距离为6。1、已知：如图，线段AB与⊙O交于C、D两点，且OA=OB ．求证：AC=BD ．灵活运用: 在以O为圆心的两个圆心圆中，大圆的弦AB交小圆于C、D两点，
求证：AC=BDH变一变:D 2、已知在⊙O中，弦AB的长为8cm，圆心O到AB的距离为3cm，求⊙O的半径。灵活运用:
3、圆内一条弦CD和直径AB相交成300角，且分直径AB成PA、PB两部分，PA=1cm，PB=5cm，则圆心到该弦距离为 （ ）
A、1/2cm B、1cm C、2cm D、2.5cm D灵活运用: 4、在Rt△ABC中∠C=900，AC=5cm，BC=12cm，以C为圆心，CA为半径的圆交斜边于D，求AD。H灵活运用: 5、已知在⊙O中，OB=10cm，OE=12cm，∠E=300，则AB= cm。D灵活运用:6、在直径为650mm的圆柱形油槽内装入一些油后，截面如图所示，若油面宽AB=600mm，求油的最大深度。灵活运用: 7、 1300年前，我国隋朝建造的赵州石拱桥的桥拱是圆弧形，它的跨度（弧所对的弦的长）为37.4米，拱高（弧的中点到弦的距离，也叫弓形高）为7.2米，求桥 拱的半径（精确到0.1米）灵活运用: 例3、⊙O1与⊙O2相交于A、B两点，P为O1O2的中点，直线CD经过A点，且PA⊥CD于A点，CD分别交⊙O1、⊙O2于C、D，
求证：CA=DA。PCDMN (变式一) ⊙O1与⊙O2相交于A、B两点，过点A作O1O2的平行线，与两圆相交于点C、D，式试猜想CD与O1O2的关系。 MN（变式二）如图甲、乙，AB是⊙O的直径，CD是⊙O的弦，图甲中，AE⊥CD于E，BF⊥CD于F，图乙中，
MC⊥CD，ND⊥CD，分别交AB于M、N。
（1）求证；图甲中CE=DF
（2）图乙中AM与BN大小怎样？为什么？MM　（3）若图甲、乙中的弦CD与直径相交于点P，其他条件不变，请画出相应的图形，并写出与（1）、（2）两问相类似的正确结论。（不必证明）ＭＣＥＦＤＮＣＤHH 例5、在半径为5的圆中,弦AB∥CD,AB=6,
CD=8,试求AB和CD的距离. 猜想线段AC的长度有几种？BACDBACD1、已知⊙O的半径为13cm，圆心O到弦AB的弦心距为5cm， 求弦AB的长。做一做2、在半径为50㎜的圆O中，有长50㎜的弦AB，计算：
⑴点O与AB的距离； ⑵∠AOB的度数。A4、如图，⊙O的直径为10，弦AB长为8，M是弦AB上的动点，则OM的长的取值范围是（ ）
A．3≤OM≤5 B．4≤OM≤5
C．3 DE=1cm，EF=3cm，则AB=______cm5GHMN课堂小结垂径定理题设结论（1）过圆心
（2）垂直于弦｝｛（3）平分弦
（4）平分弦所对的优弧
（5）平分弦所对的劣弧船能过拱桥吗 如图,某地有一圆弧形拱桥,桥下水面宽为7.2米,拱顶高出水面2.4米.现有一艘宽3米、船舱顶部为长方形并高出水面2米的货船要经过这里,此货船能顺利通过这座拱桥吗？相信自己能独立完成解答.拓展延伸:结束寄语再见形成天才的决定因素应该是勤奋.