4.4.1 对数函数的概念 课件(23张PPT)
文档属性
| 名称 | 4.4.1 对数函数的概念 课件(23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 12:13:01 | ||
图片预览








文档简介
(共23张PPT)
4.4.1对数函数的概念
单击此处添加副标题
考古学家推测出土文物或古遗址年代的的重要方法:碳14测年法
三星堆出土的文物
千年睡美人—辛追复原图
热点链接
4.2.1问题2:当生物死亡后,它机体内原有的碳14含量会按确定的比率衰减(称为衰减率),大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.按照上述变化规律,生物体内碳14含量与死亡年数之间有怎样的关系?
情境回顾
设生物死亡年数为,死亡生物体内碳14含量为y
指数函数模型研究了呈指数增长或衰减变化规律的问题.
知识回顾
指数函数
问题2:这是函数吗?
问题1:由死亡生物体内碳14含量y,如何求出它的死亡年数x呢?
新知探究
函数的概念:
对于中任意一个数,按对应关系
在中是否都有唯一确定的数与之对应?
设,是非空的实数集,如果对于集合A中的任意一个数,按照某种确定的对应关系,在集合中都有唯一确定的数和它对应,那么就称 :A→B为从集合A到集合的一个函数,记作
新知探究
新知探究
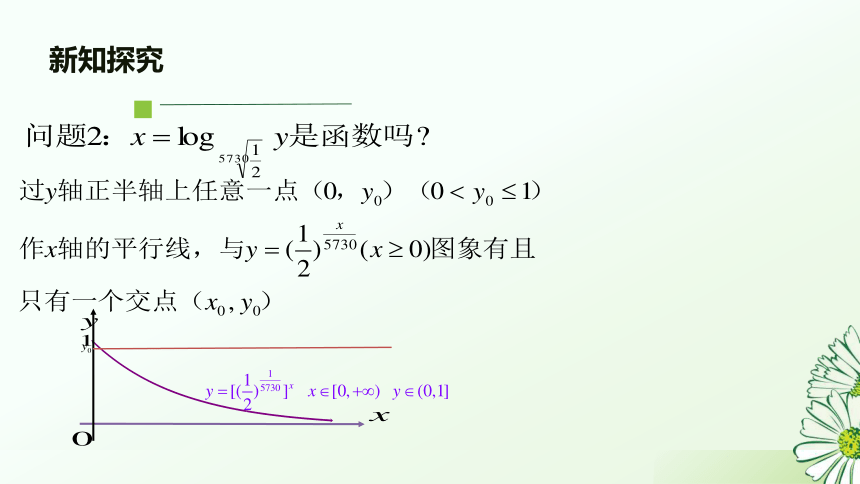
问题2: 是函数吗?
新知探究
问题3 如果将底数换为其它常数,x还是y的函数吗?
新知探究
=
是
是
问题4:
问题5:这个函数有什么特征?
此函数自变量:
通常函数自变量:
因变量:
因变量:
y
x
x
y
新知探究
指数函数
对数函数
问题6 把底数抽象化,你能得到什么一般性的结论?
新知探究
一般地
=
=
=
对概念的深度剖析:
(1)对数函数的定义是形式定义,形式特征:
系数:对数符号前面的系数是____;
底数:__________________ ;
真数:对数的真数仅有自变量x.
1
a>0,且a≠1
新知学习
对数函数的概念:
一般地,函数叫做对数函数,其中是自变量,定义域是.
判断依据
例1:给出下列函数:
①y=logax(a∈R);② ;③y=lgx ; y=log3(x+2); y=2log4x
其中所有对数函数的序号是( )
②
③
题型一:对数函数的概念
题型一:对数函数的概念
练习:函数是对数函数,
则
解:∵,解得或-3.
而∴.即
∴
(2)对数函数中的底数和对数运算中的底数相同,都是_____________.
(3)对数的运算中N>0,对数函数中的自变量_____________ ,对数函数的定义域是_____________.
a>0,且a≠1
(0,+∞)
对概念的深度剖析:
(1)对数函数的定义是形式定义,函数特征(对数函数的判断依据):
系数:对数符号前面的系数是1;
底数:a>0,且a≠1 ;
真数:对数的真数仅有自变量x.
新知学习
x>0
题型二:对数型函数的定义域
(2)因为4-x>0,即x<4,
所以函数y=loga(4-x)的定义域是{x|x<4}.
解:(1)因为x >0,即x≠0,
所以函数y=log3x 的定义域是{x|x≠0}.
注意:先求定义域,再化简!
解:由
题型二:对数型函数的定义域
所以函数f(x)+的
定义域为(-1,0)U[0,3].
解得-1物价x 1 2 3 4 5 6 7 8 9 10
年数y 0
题型三:对数函数在实际问题中的应用
题型三:对数函数在实际问题中的应用
由对数与指数间的关系可得,
物价x 1 2 3 4 5 6 7 8 9 10
年数y 0 14 23 28 33 37 40 43 45 47
物价x 1 2 3 4 5 6 7 8 9 10
年数y 0
题型三:对数函数在实际问题中的应用
题型三:对数函数在实际问题中的应用
物价x 1 2 3 4 5 6 7 8 9 10
年数y 0
物价x 1 2 3 4 5 6 7 8 9 10 年数y 0 14 23 28 33 37 40 43 45 47 相邻年数差 ↘ ↙↘ ↙↘ ↙↘ ↙↘ ↙↘ ↙↘ ↙↘ ↙↘ ↙ 14 9 5 5 4 3 3 2 2
物价x 1 2 3 4 5 6 7 8 9 10
年数y 0
物价x 1 2 3 4 5 6 7 8 9 10
年数y 0 14 23 28 33 37 40 43 45 47
题型三:对数函数在实际问题中的应用
3
2
1
对数函数的概念
对数函数的理解
对数模型的实际应用
判断对数函数
求定义域
(1)(2)
课堂小结
4.4.1对数函数的概念
单击此处添加副标题
考古学家推测出土文物或古遗址年代的的重要方法:碳14测年法
三星堆出土的文物
千年睡美人—辛追复原图
热点链接
4.2.1问题2:当生物死亡后,它机体内原有的碳14含量会按确定的比率衰减(称为衰减率),大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.按照上述变化规律,生物体内碳14含量与死亡年数之间有怎样的关系?
情境回顾
设生物死亡年数为,死亡生物体内碳14含量为y
指数函数模型研究了呈指数增长或衰减变化规律的问题.
知识回顾
指数函数
问题2:这是函数吗?
问题1:由死亡生物体内碳14含量y,如何求出它的死亡年数x呢?
新知探究
函数的概念:
对于中任意一个数,按对应关系
在中是否都有唯一确定的数与之对应?
设,是非空的实数集,如果对于集合A中的任意一个数,按照某种确定的对应关系,在集合中都有唯一确定的数和它对应,那么就称 :A→B为从集合A到集合的一个函数,记作
新知探究
新知探究
问题2: 是函数吗?
新知探究
问题3 如果将底数换为其它常数,x还是y的函数吗?
新知探究
=
是
是
问题4:
问题5:这个函数有什么特征?
此函数自变量:
通常函数自变量:
因变量:
因变量:
y
x
x
y
新知探究
指数函数
对数函数
问题6 把底数抽象化,你能得到什么一般性的结论?
新知探究
一般地
=
=
=
对概念的深度剖析:
(1)对数函数的定义是形式定义,形式特征:
系数:对数符号前面的系数是____;
底数:__________________ ;
真数:对数的真数仅有自变量x.
1
a>0,且a≠1
新知学习
对数函数的概念:
一般地,函数叫做对数函数,其中是自变量,定义域是.
判断依据
例1:给出下列函数:
①y=logax(a∈R);② ;③y=lgx ; y=log3(x+2); y=2log4x
其中所有对数函数的序号是( )
②
③
题型一:对数函数的概念
题型一:对数函数的概念
练习:函数是对数函数,
则
解:∵,解得或-3.
而∴.即
∴
(2)对数函数中的底数和对数运算中的底数相同,都是_____________.
(3)对数的运算中N>0,对数函数中的自变量_____________ ,对数函数的定义域是_____________.
a>0,且a≠1
(0,+∞)
对概念的深度剖析:
(1)对数函数的定义是形式定义,函数特征(对数函数的判断依据):
系数:对数符号前面的系数是1;
底数:a>0,且a≠1 ;
真数:对数的真数仅有自变量x.
新知学习
x>0
题型二:对数型函数的定义域
(2)因为4-x>0,即x<4,
所以函数y=loga(4-x)的定义域是{x|x<4}.
解:(1)因为x >0,即x≠0,
所以函数y=log3x 的定义域是{x|x≠0}.
注意:先求定义域,再化简!
解:由
题型二:对数型函数的定义域
所以函数f(x)+的
定义域为(-1,0)U[0,3].
解得-1
年数y 0
题型三:对数函数在实际问题中的应用
题型三:对数函数在实际问题中的应用
由对数与指数间的关系可得,
物价x 1 2 3 4 5 6 7 8 9 10
年数y 0 14 23 28 33 37 40 43 45 47
物价x 1 2 3 4 5 6 7 8 9 10
年数y 0
题型三:对数函数在实际问题中的应用
题型三:对数函数在实际问题中的应用
物价x 1 2 3 4 5 6 7 8 9 10
年数y 0
物价x 1 2 3 4 5 6 7 8 9 10 年数y 0 14 23 28 33 37 40 43 45 47 相邻年数差 ↘ ↙↘ ↙↘ ↙↘ ↙↘ ↙↘ ↙↘ ↙↘ ↙↘ ↙ 14 9 5 5 4 3 3 2 2
物价x 1 2 3 4 5 6 7 8 9 10
年数y 0
物价x 1 2 3 4 5 6 7 8 9 10
年数y 0 14 23 28 33 37 40 43 45 47
题型三:对数函数在实际问题中的应用
3
2
1
对数函数的概念
对数函数的理解
对数模型的实际应用
判断对数函数
求定义域
(1)(2)
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
