4.3.1 对数的发明 课件(26张PPT)
文档属性
| 名称 | 4.3.1 对数的发明 课件(26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 9.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
对数的发明
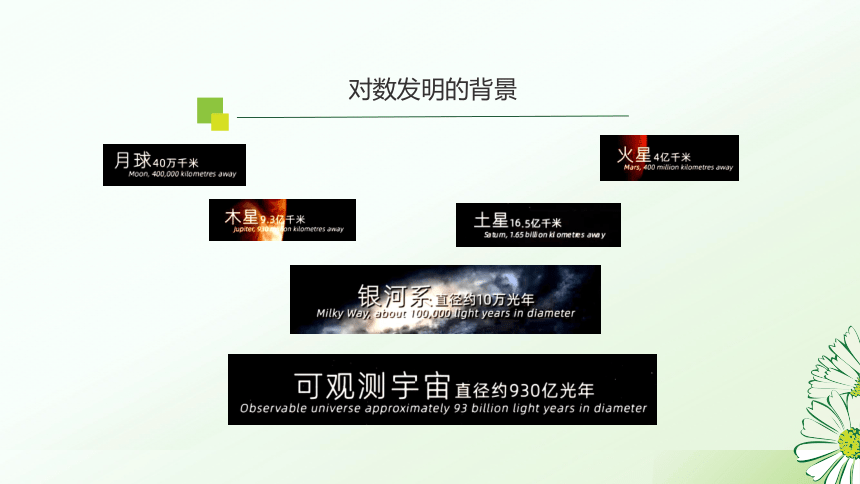
对数发明的背景
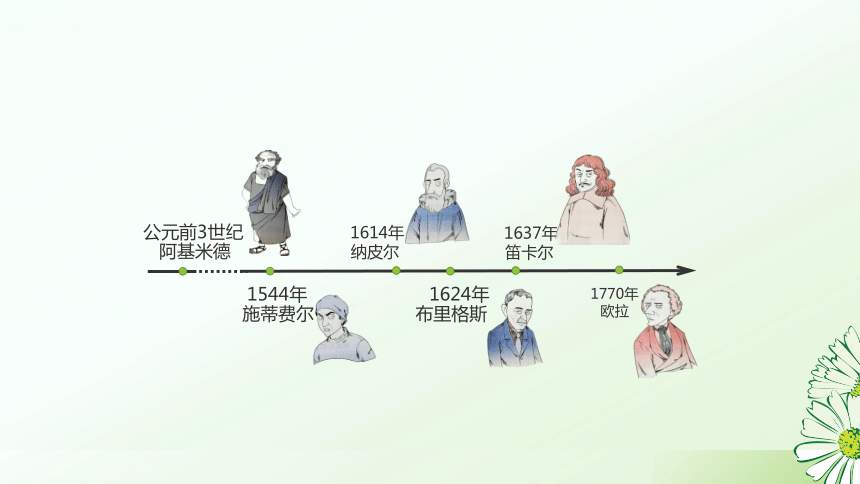
公元前3世纪
阿基米德
1544年
施蒂费尔
1614年
纳皮尔
1637年
笛卡尔
1770年
欧拉
1624年
布里格斯
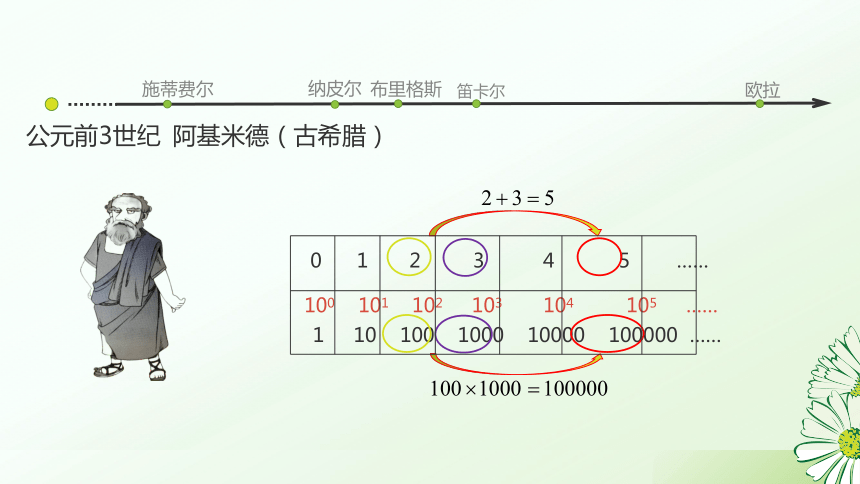
公元前3世纪 阿基米德(古希腊)
1 10 100 1000 10000 100000 ……
0 1 2 3 4 5 ……
100 101 102 103 104 105 ……
施蒂费尔
纳皮尔
笛卡尔
欧拉
布里格斯
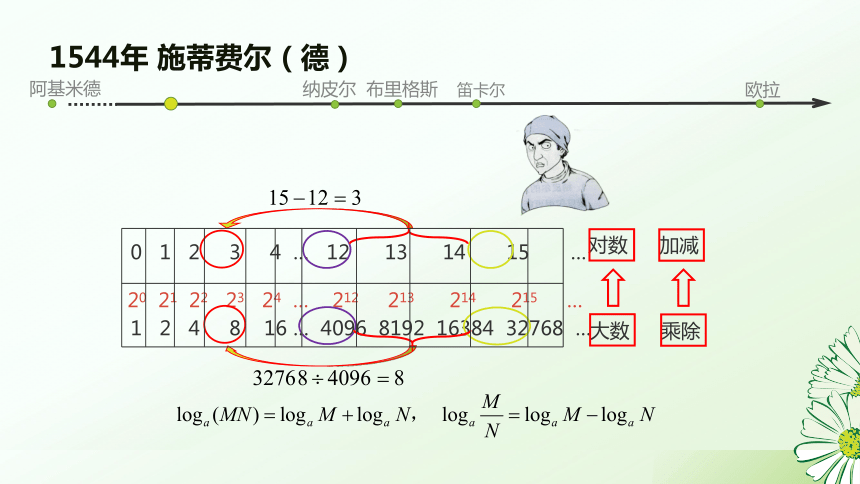
1 2 4 8 16 … 4096 8192 16384 32768 …
0 1 2 3 4 … 12 13 14 15 …
20 21 22 23 24 … 212 213 214 215 …
大数
对数
乘除
加减
纳皮尔
笛卡尔
欧拉
布里格斯
阿基米德
1544年 施蒂费尔(德)
1614年 纳皮尔(苏格兰)
苏格兰数学家 John Napier(纳皮尔,1550—1617),1614年出版《奇妙的对数定律说明书》,首次定义了“对数”,并创造了“对数”单词“logarithm”。
施蒂费尔
笛卡尔
欧拉
布里格斯
阿基米德
1614年 纳皮尔(苏格兰)
纳皮尔借助运动学,用几何术语阐述了对数方法,并发布了第一张对数表,风靡欧洲。
施蒂费尔
笛卡尔
欧拉
布里格斯
阿基米德
图源:观风闻网站
数学建模
探究活动一:
请同学们仔细阅读课本 128页第二段,认真思考,小组讨论,尝试写出x与y的函数关系。
x 0 1 2 3 4 5 6 … n
y
连续
离散
数学建模
P近似匀速运动:
A
B
P1
C
D
Q1
Q匀速运动:
(初速度相同)
逻辑推理
P近似匀速运动:
A
B
P1
C
D
Q1
Q匀速运动:
Q2
P2
P1处的瞬时速度
逻辑推理
x 0 1 2 3 4 5 6 … n
y
探究活动二:
请同学们按照以上思路,继续推理,完成表格,归纳函数关系。
逻辑推理
q = = 0.9999 999
x 0 1 2 3 … n
y …
逻辑推理
q = = 0.9999 999
x 0 1 2 3 … n
y …
1000 0000 999 9999 999 9998 999 9997 …
…
数学运算
x … … … … …
y … N … M …
探究活动三:
如何利用纳皮尔对数表求出两个正整数M和N的积与商呢?请你为它写一份使用说明书。
数学运算
x … b … … a … …
y … N … … M … …
a-b
a+b
L
K
数学运算
数学运算
1624年 布里格斯(英)
亨利·布里格斯(1561—1631),伦敦格雷欣学院几何教授,牛津大学首任萨维尔数学教授。1624年出版了《对数算术》,公布了以10为底数的常用对数表。
施蒂费尔
纳皮尔
笛卡尔
欧拉
阿基米德
2 9 9 7 9 2 4 5 8
× 3 1 5 3 6
1 7 9 8 7 5 4 7 4 8
8 9 9 3 7 7 3 7 4
1 4 9 8 9 6 2 2 9 0
2 9 9 7 9 2 4 5 8
8 9 9 3 7 7 3 7 4
9 4 5 4 2 5 4 9 5 5 4 8 8
例: 一光年的计算
图源:《数学手册》
例:一光年的计算
a=lg 299792458
b=lg 31536
一光年=
=9 454 254 955 488
数学运算
1637年 笛卡尔(法)
1637年,法国数学家笛卡尔(1596—1650)出版巨著《方法论》,开始使用指数符号ax,标志着指数的发明。
施蒂费尔
纳皮尔
欧拉
布里格斯
阿基米德
1770年 欧拉(瑞士)
1770年,瑞士数学家欧拉,发现了指数与对数的互逆关系,并在其著作中首先使用y=ax来定义x=logay,真正解决对数的连续问题。欧拉指出,“对数源出于指数”。
施蒂费尔
纳皮尔
笛卡尔
布里格斯
阿基米德
萌芽
发明
特殊正整数对应的整数指数
任意正整数对应的小数指数
任意正数对应的实数指数
完善
1544年
施蒂费尔
1614年
纳皮尔
1637年
笛卡尔
1770年
欧拉
1624年
布里格斯
公元前3世纪
阿基米德
运算降级:
乘法→加法,除法→减法,乘方→乘法,开方→除法
课堂小结
对数发明和发展过程中,你还有哪些感兴趣的事,请你继续查阅资料,写一篇读书笔记。参考话题:
1. 约斯特·伯基为什么与“对数发明者”失之交臂?
2. 如何使用对数计算尺?
3. 我国戴煦等数学家,在对数方面也有深入的研究,你知道他们的贡献吗?
课后作业
推荐书籍:
《数学欣赏》必修第一册,人民教育出版社.
《中学数学简史》,科学出版社.
《数学史》,译林出版社.
《这才是好读的数学史》,北京时代华文书局.
课后作业
对数的发明
对数发明的背景
公元前3世纪
阿基米德
1544年
施蒂费尔
1614年
纳皮尔
1637年
笛卡尔
1770年
欧拉
1624年
布里格斯
公元前3世纪 阿基米德(古希腊)
1 10 100 1000 10000 100000 ……
0 1 2 3 4 5 ……
100 101 102 103 104 105 ……
施蒂费尔
纳皮尔
笛卡尔
欧拉
布里格斯
1 2 4 8 16 … 4096 8192 16384 32768 …
0 1 2 3 4 … 12 13 14 15 …
20 21 22 23 24 … 212 213 214 215 …
大数
对数
乘除
加减
纳皮尔
笛卡尔
欧拉
布里格斯
阿基米德
1544年 施蒂费尔(德)
1614年 纳皮尔(苏格兰)
苏格兰数学家 John Napier(纳皮尔,1550—1617),1614年出版《奇妙的对数定律说明书》,首次定义了“对数”,并创造了“对数”单词“logarithm”。
施蒂费尔
笛卡尔
欧拉
布里格斯
阿基米德
1614年 纳皮尔(苏格兰)
纳皮尔借助运动学,用几何术语阐述了对数方法,并发布了第一张对数表,风靡欧洲。
施蒂费尔
笛卡尔
欧拉
布里格斯
阿基米德
图源:观风闻网站
数学建模
探究活动一:
请同学们仔细阅读课本 128页第二段,认真思考,小组讨论,尝试写出x与y的函数关系。
x 0 1 2 3 4 5 6 … n
y
连续
离散
数学建模
P近似匀速运动:
A
B
P1
C
D
Q1
Q匀速运动:
(初速度相同)
逻辑推理
P近似匀速运动:
A
B
P1
C
D
Q1
Q匀速运动:
Q2
P2
P1处的瞬时速度
逻辑推理
x 0 1 2 3 4 5 6 … n
y
探究活动二:
请同学们按照以上思路,继续推理,完成表格,归纳函数关系。
逻辑推理
q = = 0.9999 999
x 0 1 2 3 … n
y …
逻辑推理
q = = 0.9999 999
x 0 1 2 3 … n
y …
1000 0000 999 9999 999 9998 999 9997 …
…
数学运算
x … … … … …
y … N … M …
探究活动三:
如何利用纳皮尔对数表求出两个正整数M和N的积与商呢?请你为它写一份使用说明书。
数学运算
x … b … … a … …
y … N … … M … …
a-b
a+b
L
K
数学运算
数学运算
1624年 布里格斯(英)
亨利·布里格斯(1561—1631),伦敦格雷欣学院几何教授,牛津大学首任萨维尔数学教授。1624年出版了《对数算术》,公布了以10为底数的常用对数表。
施蒂费尔
纳皮尔
笛卡尔
欧拉
阿基米德
2 9 9 7 9 2 4 5 8
× 3 1 5 3 6
1 7 9 8 7 5 4 7 4 8
8 9 9 3 7 7 3 7 4
1 4 9 8 9 6 2 2 9 0
2 9 9 7 9 2 4 5 8
8 9 9 3 7 7 3 7 4
9 4 5 4 2 5 4 9 5 5 4 8 8
例: 一光年的计算
图源:《数学手册》
例:一光年的计算
a=lg 299792458
b=lg 31536
一光年=
=9 454 254 955 488
数学运算
1637年 笛卡尔(法)
1637年,法国数学家笛卡尔(1596—1650)出版巨著《方法论》,开始使用指数符号ax,标志着指数的发明。
施蒂费尔
纳皮尔
欧拉
布里格斯
阿基米德
1770年 欧拉(瑞士)
1770年,瑞士数学家欧拉,发现了指数与对数的互逆关系,并在其著作中首先使用y=ax来定义x=logay,真正解决对数的连续问题。欧拉指出,“对数源出于指数”。
施蒂费尔
纳皮尔
笛卡尔
布里格斯
阿基米德
萌芽
发明
特殊正整数对应的整数指数
任意正整数对应的小数指数
任意正数对应的实数指数
完善
1544年
施蒂费尔
1614年
纳皮尔
1637年
笛卡尔
1770年
欧拉
1624年
布里格斯
公元前3世纪
阿基米德
运算降级:
乘法→加法,除法→减法,乘方→乘法,开方→除法
课堂小结
对数发明和发展过程中,你还有哪些感兴趣的事,请你继续查阅资料,写一篇读书笔记。参考话题:
1. 约斯特·伯基为什么与“对数发明者”失之交臂?
2. 如何使用对数计算尺?
3. 我国戴煦等数学家,在对数方面也有深入的研究,你知道他们的贡献吗?
课后作业
推荐书籍:
《数学欣赏》必修第一册,人民教育出版社.
《中学数学简史》,科学出版社.
《数学史》,译林出版社.
《这才是好读的数学史》,北京时代华文书局.
课后作业
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
