5.3 诱导公式 课件(34张PPT)
文档属性
| 名称 | 5.3 诱导公式 课件(34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 12:19:46 | ||
图片预览





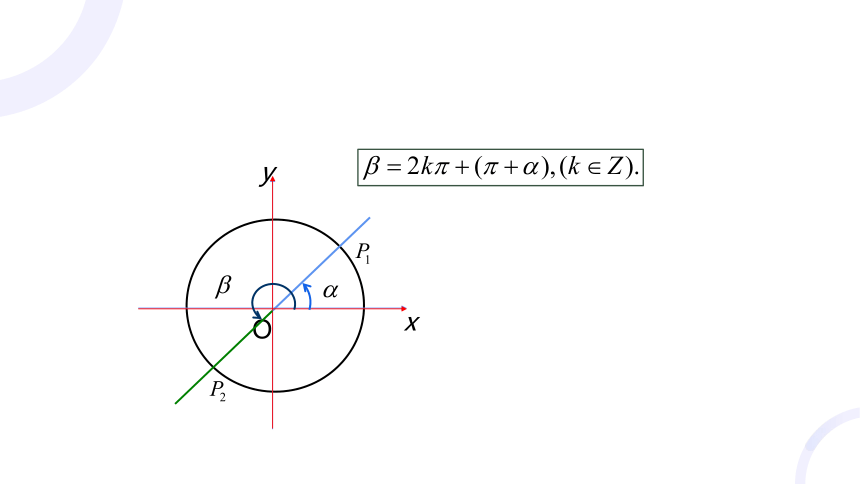
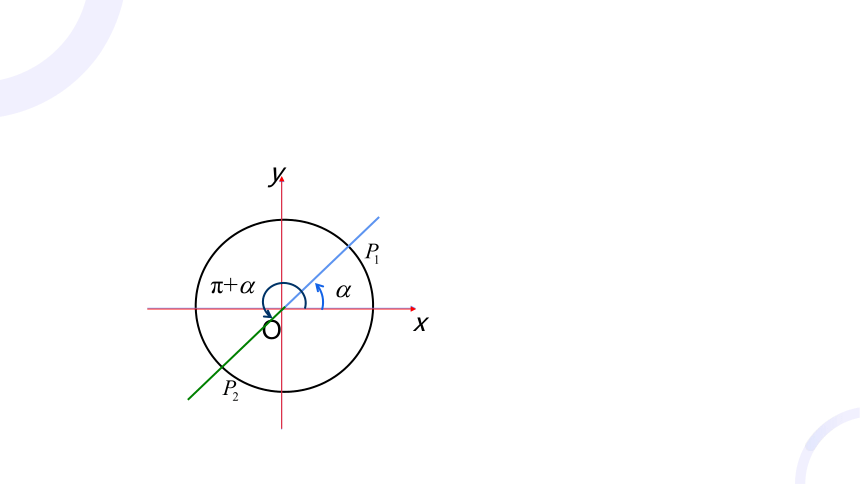
文档简介
(共34张PPT)
诱导公式
一切立体图形中最美的是球,一切平面图形中最美的是圆.
——毕达哥拉斯
x
y
O
P(x,y)
前面我们学习了三角函数,是借助于单位圆给出的,并根据定义得出了诱导公式一,刻画“周而复始”这种变化规律及其几何意义.之后利用单位圆的几何性质,结合定义,获得了同角三角函数之间的基本关系.
事实上,圆的最重要的性质是对称性,而对称性(如奇偶性)也是函数的重要性质.由此想到,我们可以利用圆的对称性,研究三角函数的对称性.
圆的对称性
问题1:
在直角坐标系中能找到单位圆的哪些特殊对称性呢?如图,在直角坐标系内,若设任意角α的终边与单位圆交于点P1,你能想到单位圆上点P1的哪些特殊对称点?
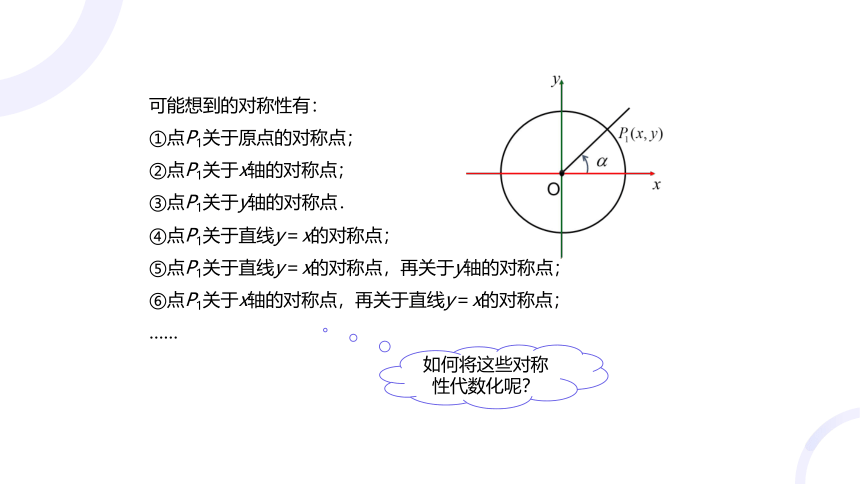
可能想到的对称性有:
①点P1关于原点的对称点;
②点P1关于x轴的对称点;
③点P1关于y轴的对称点.
追问 如果允许在坐标系内添加直线,你又能想到哪些?如果允许做两次对称变换,你还能想到哪些?
④点P1关于直线y=x的对称点;
⑤点P1关于直线y=x的对称点,再关于y轴的对称点;
⑥点P1关于x轴的对称点,再关于直线y=x的对称点;
……
如何将这些对称性代数化呢?
可能想到的对称性有:
①点P1关于原点的对称点;
②点P1关于x轴的对称点;
③点P1关于y轴的对称点.
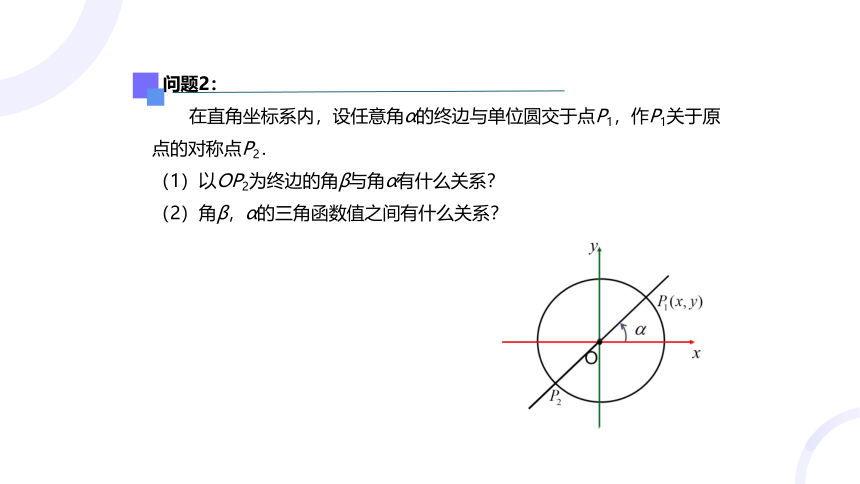
问题2:
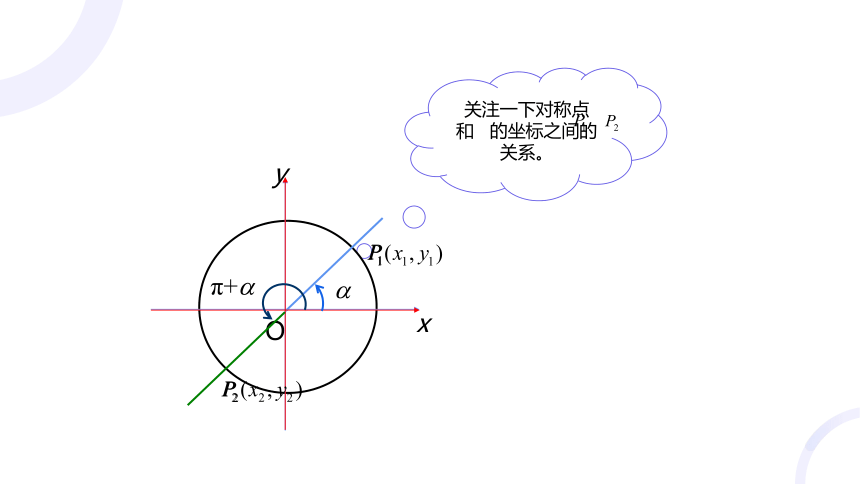
在直角坐标系内,设任意角α的终边与单位圆交于点P1,作P1关于原点的对称点P2.
(1)以OP2为终边的角β与角α有什么关系?
(2)角β,α的三角函数值之间有什么关系?
x
y
O
x
y
O
关注一下对称点 和 的坐标之间的关系。
x
y
O
x
y
O
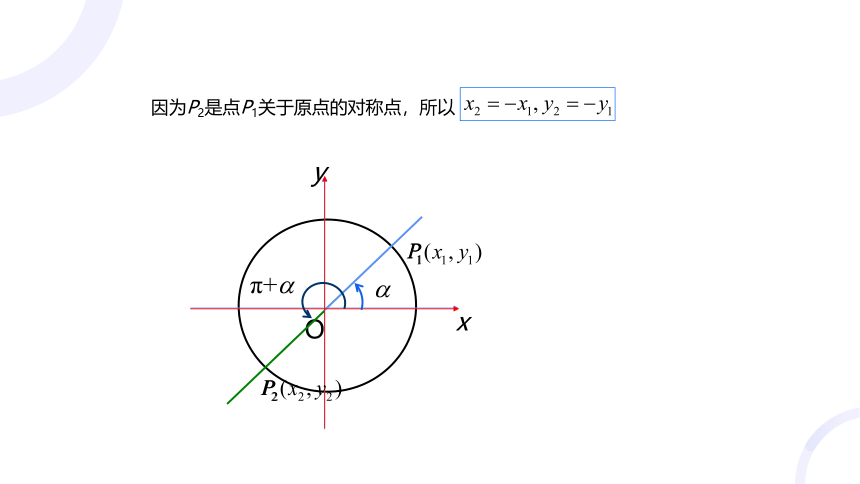
因为P2是点P1关于原点的对称点,所以
x
y
O
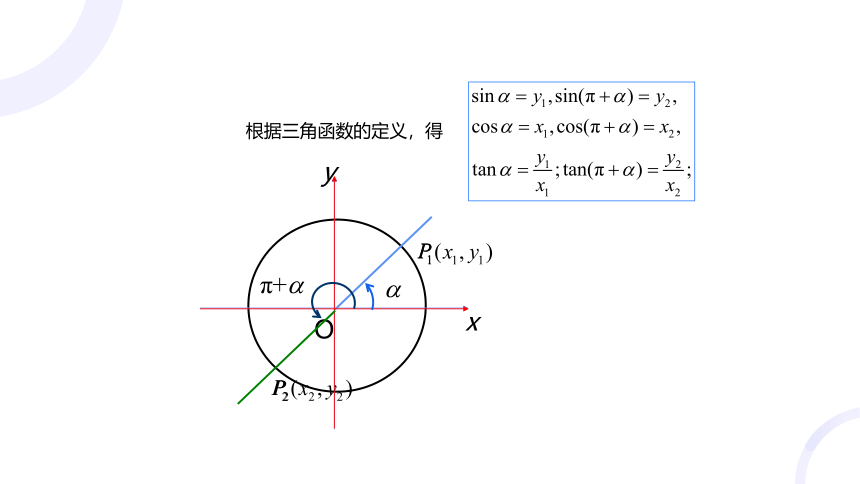
根据三角函数的定义,得
公式二:
追问1
上述推导过程中用到点P1所在位置的条件了吗?如果点P1在第二象限,那么点P2的坐标与点P1的坐标之间有什么关系?如果点P1在y轴负半轴上呢?在其他位置呢?据此,公式二中的角α的大小是多少?
回顾推导过程,发现不论点P1在哪里,点P2的坐标与点P1的坐标之间的关系都不变.
即对于正弦和余弦的诱导公式, 可以是任意角;对于正切的诱导公式, 的终边不能落在y轴上,即
追问2
探究公式二的过程,可以概括为哪些步骤?每一步蕴含的数学思想是什么?
第一步,根据圆的对称性,建立角之间的联系;
第三步,等量代换,得到三角函数值的关系.
第二步,形的关系代数化,建立坐标之间的关系;
形
联系性
数
研究诱导公式的一般套路
追问3
角π+α还可以看作是角α的终边经过怎样的变换得到的?
结论:角α的终边按逆时针方向旋转角π得到的.
问题3:
请你类比公式二的研究思路,如果作 关于x轴(或y轴)的对称点 (或 ),那么又可以得到什么结论?
请大家自主探究和推理论证
x
y
O
以 为终边的角 都是与角 终边相同的角,即:
因此,只要探究角 与角 的三角函数值之间的关系即可.
设
因为 是点 关于x轴的对称点
所以
作点 关于x轴的对称点
x
y
O
所以
根据三角函数的定义,得
公式三:
作点 关于x轴的对称点
x
y
O
以 为终边的角 都是与角 终边相同的角,即:
因此,只要探究角 与角 的三角函数值之间的关系即可.
设
因为 是点 关于y轴的对称点
所以
作点 关于y轴的对称点
所以
根据三角函数的定义,得
公式四:
x
y
O
作点 关于y轴的对称点
追问
公式三和公式四中的角α是多大的角?
类比公式二我们可以知道,发现不论点P1在哪里,点P3( 或P4 )的坐标与点P1的坐标之间的关系都不变.
即对于正弦和余弦的诱导公式, 可以是任意角;对于正切的诱导公式, 的终边不能落在y轴上,即
诱导公式一~四
公式三:
公式四:
公式二:
公式一:
诱导公式一~四
的三角函数值,等于 的同名函数值,前面加上一个把 看成锐角时的原函数值的符号
例1 利用公式求下列三角函数值
分析:
题目中的角与那个特殊角接近?拆分之后应该选择哪个诱导公式
例1 利用公式求下列三角函数值
解:
例1 利用公式求下列三角函数值
解:
例1 利用公式求下列三角函数值
解:
例1 利用公式求下列三角函数值
解:
问题4:
由例1,你对公式一~公式四的作用有什么进一步的认识?你能自己归纳一下把任意角的三角函数转化为锐角三角函数的步骤吗?
任意正角的三角函数
任意负角的三角函数
锐角的三角函数
的角的三角函数
用公式三或一
用公式一
用公式二或四
例2 化简
分析:
本题与例1的异同是什么?
由例1总结出的求解程序在此如何应用?
例2 化简
小结
思考:诱导公式与三角函数和圆之间有怎样的关系?你学习了哪些基本知识,获得了怎样的研究问题的经验?
(1)诱导公式是圆的对称性的代数化,是三角函数的性质.
(2)学习了三组诱导公式,其研究方法如下:
作业
基本作业:课本191页练习1、2、3、4题.
拓展作业:你能类比公式二的研究方法,利用
④点P1关于直线y=x的对称点;
⑤点P1关于直线y=x的对称点,再关于y轴的对称点;
⑥点P1关于x轴的对称点,再关于直线y=x的对称点;
来研究三角函数的其他对称性吗?
请同学们课下继续研究。
诱导公式
一切立体图形中最美的是球,一切平面图形中最美的是圆.
——毕达哥拉斯
x
y
O
P(x,y)
前面我们学习了三角函数,是借助于单位圆给出的,并根据定义得出了诱导公式一,刻画“周而复始”这种变化规律及其几何意义.之后利用单位圆的几何性质,结合定义,获得了同角三角函数之间的基本关系.
事实上,圆的最重要的性质是对称性,而对称性(如奇偶性)也是函数的重要性质.由此想到,我们可以利用圆的对称性,研究三角函数的对称性.
圆的对称性
问题1:
在直角坐标系中能找到单位圆的哪些特殊对称性呢?如图,在直角坐标系内,若设任意角α的终边与单位圆交于点P1,你能想到单位圆上点P1的哪些特殊对称点?
可能想到的对称性有:
①点P1关于原点的对称点;
②点P1关于x轴的对称点;
③点P1关于y轴的对称点.
追问 如果允许在坐标系内添加直线,你又能想到哪些?如果允许做两次对称变换,你还能想到哪些?
④点P1关于直线y=x的对称点;
⑤点P1关于直线y=x的对称点,再关于y轴的对称点;
⑥点P1关于x轴的对称点,再关于直线y=x的对称点;
……
如何将这些对称性代数化呢?
可能想到的对称性有:
①点P1关于原点的对称点;
②点P1关于x轴的对称点;
③点P1关于y轴的对称点.
问题2:
在直角坐标系内,设任意角α的终边与单位圆交于点P1,作P1关于原点的对称点P2.
(1)以OP2为终边的角β与角α有什么关系?
(2)角β,α的三角函数值之间有什么关系?
x
y
O
x
y
O
关注一下对称点 和 的坐标之间的关系。
x
y
O
x
y
O
因为P2是点P1关于原点的对称点,所以
x
y
O
根据三角函数的定义,得
公式二:
追问1
上述推导过程中用到点P1所在位置的条件了吗?如果点P1在第二象限,那么点P2的坐标与点P1的坐标之间有什么关系?如果点P1在y轴负半轴上呢?在其他位置呢?据此,公式二中的角α的大小是多少?
回顾推导过程,发现不论点P1在哪里,点P2的坐标与点P1的坐标之间的关系都不变.
即对于正弦和余弦的诱导公式, 可以是任意角;对于正切的诱导公式, 的终边不能落在y轴上,即
追问2
探究公式二的过程,可以概括为哪些步骤?每一步蕴含的数学思想是什么?
第一步,根据圆的对称性,建立角之间的联系;
第三步,等量代换,得到三角函数值的关系.
第二步,形的关系代数化,建立坐标之间的关系;
形
联系性
数
研究诱导公式的一般套路
追问3
角π+α还可以看作是角α的终边经过怎样的变换得到的?
结论:角α的终边按逆时针方向旋转角π得到的.
问题3:
请你类比公式二的研究思路,如果作 关于x轴(或y轴)的对称点 (或 ),那么又可以得到什么结论?
请大家自主探究和推理论证
x
y
O
以 为终边的角 都是与角 终边相同的角,即:
因此,只要探究角 与角 的三角函数值之间的关系即可.
设
因为 是点 关于x轴的对称点
所以
作点 关于x轴的对称点
x
y
O
所以
根据三角函数的定义,得
公式三:
作点 关于x轴的对称点
x
y
O
以 为终边的角 都是与角 终边相同的角,即:
因此,只要探究角 与角 的三角函数值之间的关系即可.
设
因为 是点 关于y轴的对称点
所以
作点 关于y轴的对称点
所以
根据三角函数的定义,得
公式四:
x
y
O
作点 关于y轴的对称点
追问
公式三和公式四中的角α是多大的角?
类比公式二我们可以知道,发现不论点P1在哪里,点P3( 或P4 )的坐标与点P1的坐标之间的关系都不变.
即对于正弦和余弦的诱导公式, 可以是任意角;对于正切的诱导公式, 的终边不能落在y轴上,即
诱导公式一~四
公式三:
公式四:
公式二:
公式一:
诱导公式一~四
的三角函数值,等于 的同名函数值,前面加上一个把 看成锐角时的原函数值的符号
例1 利用公式求下列三角函数值
分析:
题目中的角与那个特殊角接近?拆分之后应该选择哪个诱导公式
例1 利用公式求下列三角函数值
解:
例1 利用公式求下列三角函数值
解:
例1 利用公式求下列三角函数值
解:
例1 利用公式求下列三角函数值
解:
问题4:
由例1,你对公式一~公式四的作用有什么进一步的认识?你能自己归纳一下把任意角的三角函数转化为锐角三角函数的步骤吗?
任意正角的三角函数
任意负角的三角函数
锐角的三角函数
的角的三角函数
用公式三或一
用公式一
用公式二或四
例2 化简
分析:
本题与例1的异同是什么?
由例1总结出的求解程序在此如何应用?
例2 化简
小结
思考:诱导公式与三角函数和圆之间有怎样的关系?你学习了哪些基本知识,获得了怎样的研究问题的经验?
(1)诱导公式是圆的对称性的代数化,是三角函数的性质.
(2)学习了三组诱导公式,其研究方法如下:
作业
基本作业:课本191页练习1、2、3、4题.
拓展作业:你能类比公式二的研究方法,利用
④点P1关于直线y=x的对称点;
⑤点P1关于直线y=x的对称点,再关于y轴的对称点;
⑥点P1关于x轴的对称点,再关于直线y=x的对称点;
来研究三角函数的其他对称性吗?
请同学们课下继续研究。
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
