2.5.1 直线与圆的位置关系 课件(20张PPT)
文档属性
| 名称 | 2.5.1 直线与圆的位置关系 课件(20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 12:32:45 | ||
图片预览







文档简介
(共20张PPT)
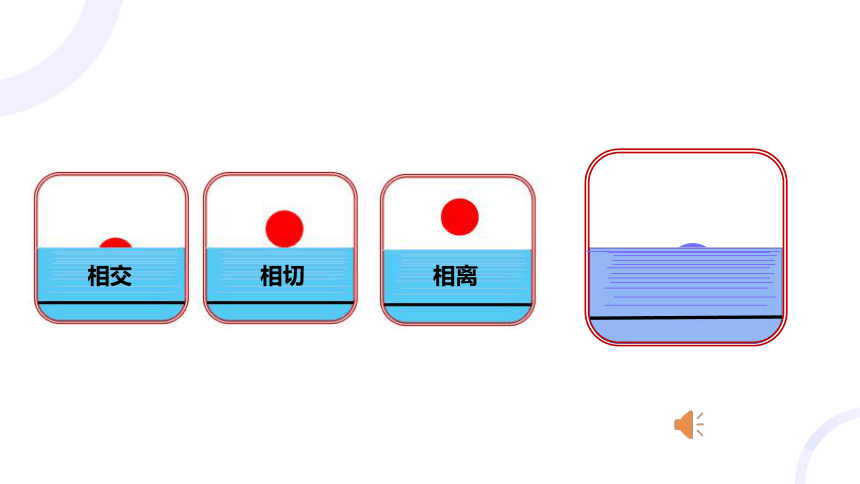
2.5.1直线与圆的位置关系
相交
相切
相离
1.掌握直线与圆的位置关系,提升直观想象、
数学抽象的学科素养.(重点)
2.会用直线和圆的方程判断直线与圆的位置关系,
提升逻辑推理、数学运算的学科素养.(重点)
3.在学习过程中,逐步理解用坐标法解决几何问题的基
本思想和方法.提高分析问题、解决问题的能力.(难点)
学习目标
2
1
0
dd=r
d>r
直线与圆公共点个数
d与r的关系
位置关系
相交
相切
相离
d
d
d
d
l
l
l
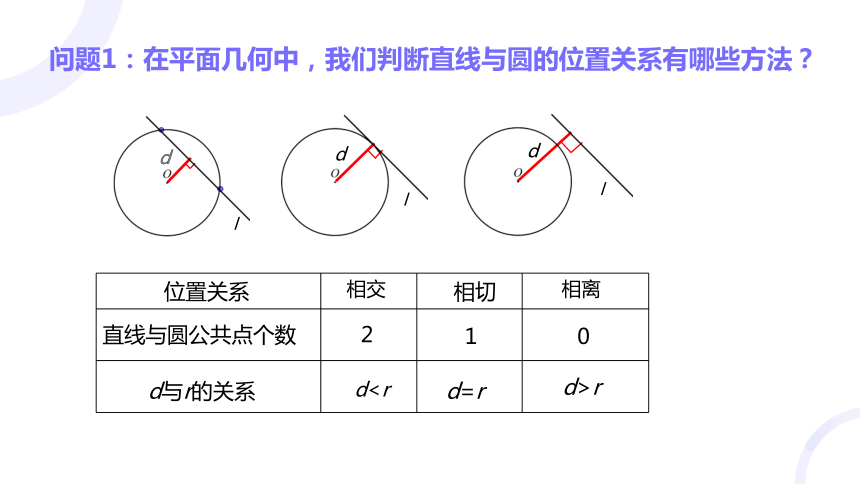
问题1:在平面几何中,我们判断直线与圆的位置关系有哪些方法?
相交
相切
相离
2
1
0
dd=r
d>r
直线与圆公
共点个数
直线与圆位置关系
圆心到直线的距离
d与r的关系
问题2:类比两直线的位置关系的研究方法,如何通过方程,研究直线与圆的位置关系?
A
交点A
直线与相交.
问题2:类比两直线的位置关系的研究方法,如何通过方程,研究直线与圆的位置关系?
两直线的位置关系
联立直线方程
方程组解的情况
几何问题
代数问题
几何图形的性质
代数方法
形
数
形
数
问题2:类比两直线的位置关系的研究方法,如何通过方程,研究直线与圆的位置关系?
两直线的
位置关系
联立两直线
的方程
方程组解的情况
直线与圆的位置关系
联立直线与圆的方程
方程组解的情况
追问:还有没有其他判断直线与圆的位置关系的方法呢?
直线与圆的位置关系
求d与r
比较d与r 的大小
d
d
d
d
l
l
l
(1)判断直线与圆C的位置关系;
(2)如果相交,求直线被圆C所截得的弦长.
思路1:将判断直线与圆的位置关系,转化为判断由它们的方程组成的方程组有无实数解、有几个实数解的问题;若相交,可以由方程组解得两交点的坐标,利用两点间的距离公式求得弦长.
解:(1)联立直线与圆的方程
所以,直线与圆C相交有两个公共点.
方程组有两组实数解.
解法一:代数法
方程组有两组实数解
相交
方程组有一组实数解
相切
方程组没有实数解
相离
因此,直线截得的弦长为
(2)由(1)可知,解得
所以直线与圆的两个交点是
(2)如果相交,求直线被圆C所截得的弦长.
B
C
A
将
(1)判断直线与圆C的位置关系;
(2)如果相交,求直线被圆C所截得的弦长.
思路2:将判断直线与圆的位置关系,转化为圆心到直线距离与半径的大小关系的问题;若相交,利用圆的几何性质--垂径定理,解决弦长问题.
解:(1) 圆的方程可化为=5,
所以,直线与圆相交,有两个公共点.
圆心= = <
因此圆心的坐标为,半径为,
解法二:几何法
(1) 判断直线与圆C的位置关系;
(2)如图
B
C
A
D
(2)如果相交,求直线被圆C所截得的弦长
思考:用“代数法”与“几何法”判断直线与圆的位置关系各有什么特点?
其实两种方法都是通过坐标研究几何图形的位置关系,只是侧重点不一样,“几何法”更多地侧重于“形”,更多地结合了图形的几何性质,计算量相对较少;“代数法”则侧重于“数”,代数法是坐标法的重要体现,更具程序性和普适性,在此例基础上体会运用坐标法研究几何问题的一般流程,为一般化几何法和代数法做准备.
知识篇
直线与圆的位置关系
相离
相切
相交
相交弦长
两点间距离公式
圆的弦长公式
总结学习成果:
方法篇
直线与圆的位置关系
代数法
几何法
求圆心到直线的距离d与半径r
比较d与r的大小
联立方程
代入消元
求判别式
总结学习成果:
数学思想篇
渗透的数学思想
化归与转化思想
数形结合思想
类比的思想
方程思想
总结学习成果:
1.判断下列各组直线
(1)=0, 圆C
(2)=0, 圆C
(3)=0, 圆C
(4)=0 , 圆C
课后作业
2.5.1直线与圆的位置关系
相交
相切
相离
1.掌握直线与圆的位置关系,提升直观想象、
数学抽象的学科素养.(重点)
2.会用直线和圆的方程判断直线与圆的位置关系,
提升逻辑推理、数学运算的学科素养.(重点)
3.在学习过程中,逐步理解用坐标法解决几何问题的基
本思想和方法.提高分析问题、解决问题的能力.(难点)
学习目标
2
1
0
d
d>r
直线与圆公共点个数
d与r的关系
位置关系
相交
相切
相离
d
d
d
d
l
l
l
问题1:在平面几何中,我们判断直线与圆的位置关系有哪些方法?
相交
相切
相离
2
1
0
d
d>r
直线与圆公
共点个数
直线与圆位置关系
圆心到直线的距离
d与r的关系
问题2:类比两直线的位置关系的研究方法,如何通过方程,研究直线与圆的位置关系?
A
交点A
直线与相交.
问题2:类比两直线的位置关系的研究方法,如何通过方程,研究直线与圆的位置关系?
两直线的位置关系
联立直线方程
方程组解的情况
几何问题
代数问题
几何图形的性质
代数方法
形
数
形
数
问题2:类比两直线的位置关系的研究方法,如何通过方程,研究直线与圆的位置关系?
两直线的
位置关系
联立两直线
的方程
方程组解的情况
直线与圆的位置关系
联立直线与圆的方程
方程组解的情况
追问:还有没有其他判断直线与圆的位置关系的方法呢?
直线与圆的位置关系
求d与r
比较d与r 的大小
d
d
d
d
l
l
l
(1)判断直线与圆C的位置关系;
(2)如果相交,求直线被圆C所截得的弦长.
思路1:将判断直线与圆的位置关系,转化为判断由它们的方程组成的方程组有无实数解、有几个实数解的问题;若相交,可以由方程组解得两交点的坐标,利用两点间的距离公式求得弦长.
解:(1)联立直线与圆的方程
所以,直线与圆C相交有两个公共点.
方程组有两组实数解.
解法一:代数法
方程组有两组实数解
相交
方程组有一组实数解
相切
方程组没有实数解
相离
因此,直线截得的弦长为
(2)由(1)可知,解得
所以直线与圆的两个交点是
(2)如果相交,求直线被圆C所截得的弦长.
B
C
A
将
(1)判断直线与圆C的位置关系;
(2)如果相交,求直线被圆C所截得的弦长.
思路2:将判断直线与圆的位置关系,转化为圆心到直线距离与半径的大小关系的问题;若相交,利用圆的几何性质--垂径定理,解决弦长问题.
解:(1) 圆的方程可化为=5,
所以,直线与圆相交,有两个公共点.
圆心= = <
因此圆心的坐标为,半径为,
解法二:几何法
(1) 判断直线与圆C的位置关系;
(2)如图
B
C
A
D
(2)如果相交,求直线被圆C所截得的弦长
思考:用“代数法”与“几何法”判断直线与圆的位置关系各有什么特点?
其实两种方法都是通过坐标研究几何图形的位置关系,只是侧重点不一样,“几何法”更多地侧重于“形”,更多地结合了图形的几何性质,计算量相对较少;“代数法”则侧重于“数”,代数法是坐标法的重要体现,更具程序性和普适性,在此例基础上体会运用坐标法研究几何问题的一般流程,为一般化几何法和代数法做准备.
知识篇
直线与圆的位置关系
相离
相切
相交
相交弦长
两点间距离公式
圆的弦长公式
总结学习成果:
方法篇
直线与圆的位置关系
代数法
几何法
求圆心到直线的距离d与半径r
比较d与r的大小
联立方程
代入消元
求判别式
总结学习成果:
数学思想篇
渗透的数学思想
化归与转化思想
数形结合思想
类比的思想
方程思想
总结学习成果:
1.判断下列各组直线
(1)=0, 圆C
(2)=0, 圆C
(3)=0, 圆C
(4)=0 , 圆C
课后作业
