3.1.1 椭圆及其标准方程 课件(共24张PPT)
文档属性
| 名称 | 3.1.1 椭圆及其标准方程 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 00:00:00 | ||
图片预览





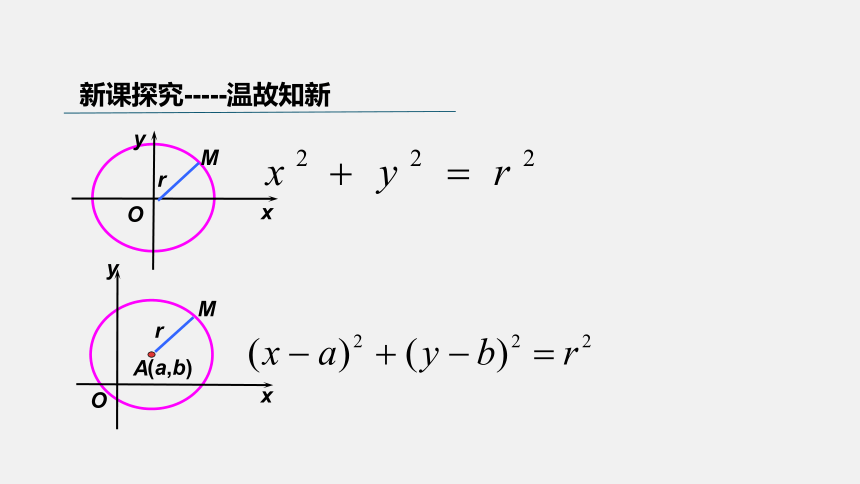


文档简介
(共24张PPT)
椭圆及其标准方程
情景引入
情景引入
情景引入
新课探究-----温故知新
1、圆的定义及圆的标准方程的推导过程?
(1)在平面内到定点的距离等于定长的
点的集合(轨迹);
(2)利用坐标法求圆的标准方程;
新课探究-----温故知新
2、用坐标法求曲线方程的步骤?
(1)建立适当的坐标系,设曲线上任意一
点M的坐标为(x,y);
(2)找出限制条件 p(M);
(3)把坐标代入限制条件p(M) ,列出方程
f (x,y)=0;
(4)化简方程 f (x,y)=0;
(5)检验(可以省略,如有特殊情况,适当说明)
建、设、限、代、化
x
O
y
M
r
x
O
A
(a,b)
M
r
y
新课探究-----温故知新
新课探究-----数学实验
[1]在纸板上确定两固定的点F1、F2
取一条不可伸缩的线绳
[2]把线绳的两端固定在F1、F2两点处
[3]用笔尖把细绳拉紧,在板上慢慢移
动看看画出的图
M
F1
F2
数学问题?
1. 椭圆定义:
平面内与两个定点 的距离的和等于常数(大于 )的点的轨迹叫作椭圆。这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距 。
|MF1|+|MF2|=2a
M
F1
F2
记焦距为2c,椭圆上的点M与F1,F2的距离和记为2a。
(|F1F2|=2c,
2a>2c>0)
注意:椭圆定义中的关键点:
(1) 平面内. ---这是大前提
(2)动点M与两定点 的距离的和等于常数2a.
(3)距离的和2a 大于焦距2c ,即2a>2c>0.
新课探究-----形成概念
距离和等于两定点间距离
即2a=2c 时,
距离和小于两定点间距离即2a<2c时,
M
F1
F2
F1
F2
为什么要求
轨迹为线段;
无轨迹。
新课探究-----理解概念
新课探究-----构建方程
建立平面直角坐标系一般遵循的原则:对称、简洁
x
O
y
方案一
方案二
x
O
y
以经过焦点F1、F2的直线为x轴,线段F1F2的垂直
平分线为y轴,建立平面直角坐标系(如图).
设M(x, y)是椭圆上任意一点,椭圆的焦距2c(c>0),
则F1、F2的坐标分别是( c,0)、(c,0) .
M与F1和F2的距离的和等于正常数2a (2a>2c)
由椭圆的定义得,限制条件:
代入坐标
化 简
建系
设点
限制
代入
检验
F1
F2
x
y
M( x , y )
新课探究-----数学运算
尝试一、
新课探究-----数学运算
尝试二、
尝试三、
新课探究-----数学运算
以经过焦点F1、F2的直线为x轴,线段F1F2的垂直
平分线为y轴,建立平面直角坐标系(如图).
设M(x, y)是椭圆上任意一点,椭圆的焦距2c(c>0),
则F1、F2的坐标分别是( c,0)、(c,0) .
M与F1和F2的距离的和等于正常数2a (2a>2c)
由椭圆的定义得,限制条件:
代入坐标
化 简
建系
设点
限制
代入
检验
化简得
F1
F2
x
y
M( x , y )
b
c
a
观察下图:你能从中找出表示 的线段吗?
新课探究-----提高辨识
焦点在y轴:
焦点在x轴:
新课探究-----推导方程
O
y
x
x
O
y
若是椭圆,请写出它的焦点坐标。
思考:下列方程哪些表示椭圆?
应用拓展-----提高能力
已知椭圆两个焦点的坐标分别是( -2, 0 )、(2,0),
并且经过点 P ,求它的标准方程.
例1:
应用拓展-----提高能力
解:因为椭圆的焦点在 轴上,设
由椭圆的定义知
所以
又因为 , 所以
因此,所求椭圆的标准方程为
定义法
x
F1
F2
P
O
y
方法一、
解:因为椭圆的焦点在 轴上,设
由于 所以
①
又点 在椭圆上
②
联立方程①②解得
因此所求椭圆的标准方程为
x
F1
F2
P
O
y
待定系数法
方法二、
一个概念:
两个方程:
两种方法:
三个意识:
|MF1|+|MF2|=2a (2a>2c>0)
定义法;待定系数法.
类比意识;求美意识;求简意识.
两种思想:
数形结合的思想;坐标法的思想.
回顾反思-----核心素养
1、必做题:
教材115页习题3.1第1、2题;
2、选做题:
求与圆 外切,且与圆
内切的动圆圆心的轨迹方程.
布置作业-----巩固新知
椭圆及其标准方程
情景引入
情景引入
情景引入
新课探究-----温故知新
1、圆的定义及圆的标准方程的推导过程?
(1)在平面内到定点的距离等于定长的
点的集合(轨迹);
(2)利用坐标法求圆的标准方程;
新课探究-----温故知新
2、用坐标法求曲线方程的步骤?
(1)建立适当的坐标系,设曲线上任意一
点M的坐标为(x,y);
(2)找出限制条件 p(M);
(3)把坐标代入限制条件p(M) ,列出方程
f (x,y)=0;
(4)化简方程 f (x,y)=0;
(5)检验(可以省略,如有特殊情况,适当说明)
建、设、限、代、化
x
O
y
M
r
x
O
A
(a,b)
M
r
y
新课探究-----温故知新
新课探究-----数学实验
[1]在纸板上确定两固定的点F1、F2
取一条不可伸缩的线绳
[2]把线绳的两端固定在F1、F2两点处
[3]用笔尖把细绳拉紧,在板上慢慢移
动看看画出的图
M
F1
F2
数学问题?
1. 椭圆定义:
平面内与两个定点 的距离的和等于常数(大于 )的点的轨迹叫作椭圆。这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距 。
|MF1|+|MF2|=2a
M
F1
F2
记焦距为2c,椭圆上的点M与F1,F2的距离和记为2a。
(|F1F2|=2c,
2a>2c>0)
注意:椭圆定义中的关键点:
(1) 平面内. ---这是大前提
(2)动点M与两定点 的距离的和等于常数2a.
(3)距离的和2a 大于焦距2c ,即2a>2c>0.
新课探究-----形成概念
距离和等于两定点间距离
即2a=2c 时,
距离和小于两定点间距离即2a<2c时,
M
F1
F2
F1
F2
为什么要求
轨迹为线段;
无轨迹。
新课探究-----理解概念
新课探究-----构建方程
建立平面直角坐标系一般遵循的原则:对称、简洁
x
O
y
方案一
方案二
x
O
y
以经过焦点F1、F2的直线为x轴,线段F1F2的垂直
平分线为y轴,建立平面直角坐标系(如图).
设M(x, y)是椭圆上任意一点,椭圆的焦距2c(c>0),
则F1、F2的坐标分别是( c,0)、(c,0) .
M与F1和F2的距离的和等于正常数2a (2a>2c)
由椭圆的定义得,限制条件:
代入坐标
化 简
建系
设点
限制
代入
检验
F1
F2
x
y
M( x , y )
新课探究-----数学运算
尝试一、
新课探究-----数学运算
尝试二、
尝试三、
新课探究-----数学运算
以经过焦点F1、F2的直线为x轴,线段F1F2的垂直
平分线为y轴,建立平面直角坐标系(如图).
设M(x, y)是椭圆上任意一点,椭圆的焦距2c(c>0),
则F1、F2的坐标分别是( c,0)、(c,0) .
M与F1和F2的距离的和等于正常数2a (2a>2c)
由椭圆的定义得,限制条件:
代入坐标
化 简
建系
设点
限制
代入
检验
化简得
F1
F2
x
y
M( x , y )
b
c
a
观察下图:你能从中找出表示 的线段吗?
新课探究-----提高辨识
焦点在y轴:
焦点在x轴:
新课探究-----推导方程
O
y
x
x
O
y
若是椭圆,请写出它的焦点坐标。
思考:下列方程哪些表示椭圆?
应用拓展-----提高能力
已知椭圆两个焦点的坐标分别是( -2, 0 )、(2,0),
并且经过点 P ,求它的标准方程.
例1:
应用拓展-----提高能力
解:因为椭圆的焦点在 轴上,设
由椭圆的定义知
所以
又因为 , 所以
因此,所求椭圆的标准方程为
定义法
x
F1
F2
P
O
y
方法一、
解:因为椭圆的焦点在 轴上,设
由于 所以
①
又点 在椭圆上
②
联立方程①②解得
因此所求椭圆的标准方程为
x
F1
F2
P
O
y
待定系数法
方法二、
一个概念:
两个方程:
两种方法:
三个意识:
|MF1|+|MF2|=2a (2a>2c>0)
定义法;待定系数法.
类比意识;求美意识;求简意识.
两种思想:
数形结合的思想;坐标法的思想.
回顾反思-----核心素养
1、必做题:
教材115页习题3.1第1、2题;
2、选做题:
求与圆 外切,且与圆
内切的动圆圆心的轨迹方程.
布置作业-----巩固新知
