3.2.1 双曲线及其标准方程 课件(24张PPT)
文档属性
| 名称 | 3.2.1 双曲线及其标准方程 课件(24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 12.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 12:37:24 | ||
图片预览






文档简介
(共24张PPT)
3.2.1双曲线及其标准方程
学习目标
1.了解双曲线的实际背景,经历从具体情境中抽象出双曲线的过程,双曲线标准方程的推导过程.
2.掌握双曲线的定义,标准方程及几何图形.(重点)
3.通过双曲线概念的引入和双曲线方程的推导,提高用坐标法解决几何问题的能力.(难点)
情境一:我们的人民海军日夜守护着海疆的安全. 某天同时段内,在 A,B两个海岛上听到了炮弹爆炸声. 已知 A,B 两地相距 800 m. 在A地听到炮弹爆炸声比在 B 地晚 2 s,且声速为 340 m/s,如何确定爆炸点的位置?
A
B
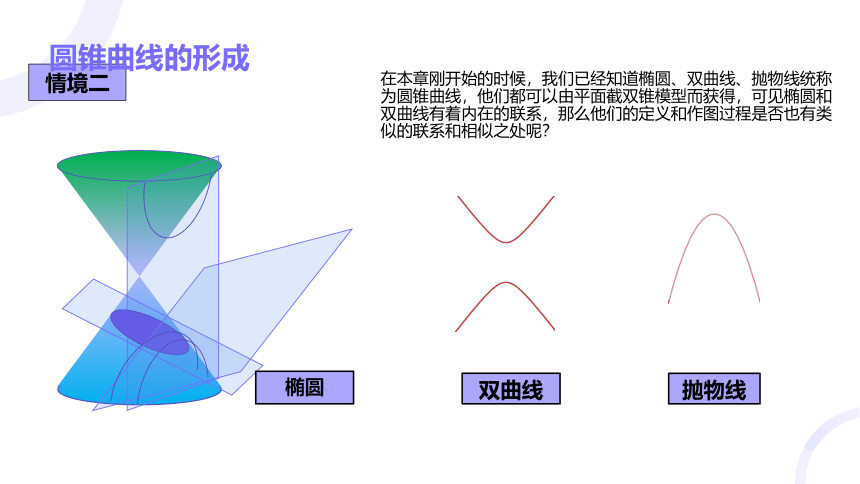
椭圆
双曲线
抛物线
情境二
在本章刚开始的时候,我们已经知道椭圆、双曲线、抛物线统称为圆锥曲线,他们都可以由平面截双锥模型而获得,可见椭圆和双曲线有着内在的联系,那么他们的定义和作图过程是否也有类似的联系和相似之处呢?
圆锥曲线的形成
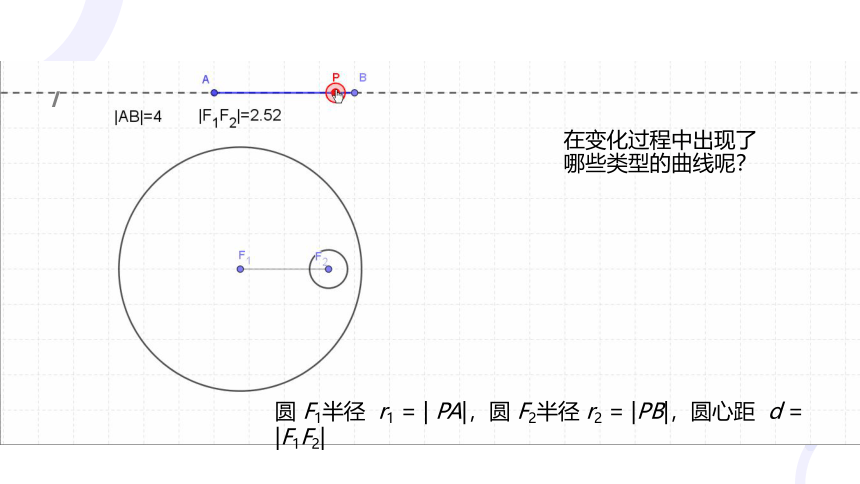
如图,在直线 l 上取两个定点 A,B,P 是直线 l 上的动点 . 在平面内,取定点 F1,F2, 以点 F1为圆心 、线段PA 为半径作圆,再以 F2 为圆心、线段 PB 为半径作圆.
圆 F1半径 r1 = | PA|,圆 F2半径 r2 = |PB|,圆心距 d = |F1F2|
l
调整 F1,F2 两点的距离,随着点 P 在直线 l 上滑动,两圆的位置和大小关系也随之改变.
当两圆相交时,交点的轨迹 M 会出现哪些图形?
圆 F1半径 r1 = | PA|,圆 F2半径 r2 = |PB|,圆心距 d = |F1F2|
l
圆 F1半径 r1 = | PA|,圆 F2半径 r2 = |PB|,圆心距 d = |F1F2|
l
在变化过程中出现了哪些类型的曲线呢?
我们知道,当点 P 在线段 AB 上运动时,如果
||PA|-|PB||<|F1F2|<|AB|,
那么两圆相交,交点M满足:
|MF1|+|MF2|=|AB|>|F1F2|.
结合椭圆的定义可知:
两圆的交点 M 的轨迹是以 F1,F2 为焦点,以线段 AB 的长为长轴长的椭圆.
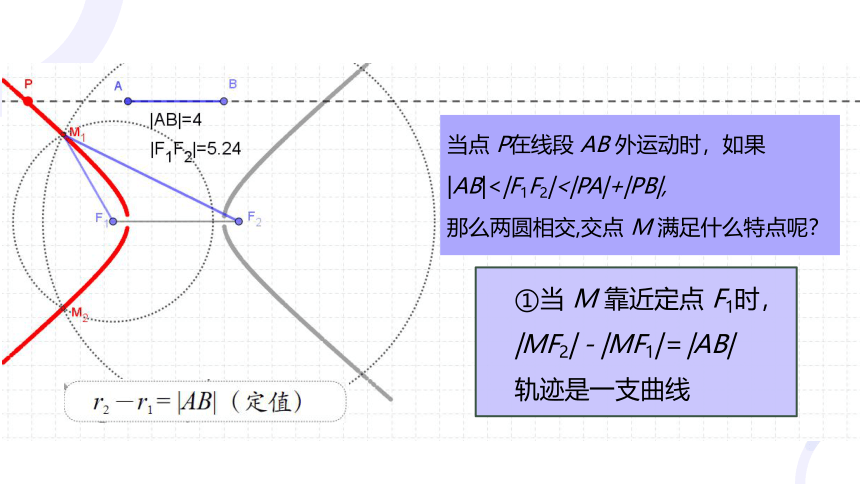
r1 +r2 =|AB|(定值)
l
①当 M 靠近定点 F1时,
|MF2|-|MF1|=|AB|
轨迹是一支曲线
当点 P在线段 AB 外运动时,如果|AB|<|F1F2|<|PA|+|PB|,
那么两圆相交,交点 M 满足什么特点呢?
②当M靠近定点F2时,
|MF1|-|MF2|=|AB|
轨迹是另一支曲线.
当点 P在线段 AB 外运动时,如果|AB|<|F1F2|<|PA|+|PB|,
那么两圆相交,交点 M 满足什么特点呢?
综上,交点 M 满足:
||MF1|-|MF2||=|AB|
(|AB|<|F1F2|)
其图像是两支曲线.
我们称之为双曲线.
双曲线的定义
一般地,我们把平面内与两个定点 F1,F2 的距离之差的绝对值等于非零常数(小于|F1F2 |)的点的轨迹叫双曲线(hyperbola).
距离之差的绝对值
非零常数
小于|F1F2|
记为2c
①这两个定点叫做双曲线的焦点.
②两焦点之间的距离叫做双曲线的焦距.
记为2a
符号表示:{ M | ||MF1|-|MF2|| = 2a < |F1F2| =2c }
若 A,B重合
则 |MF1|=|MF2|,点 M在线段 F1F2 的垂直平分线上,即点 M 的轨迹是线段 F1F2的垂直平分线 .
常数等于 0 时
若|AB|=|F1F2|且点 P在线段 AB 外运动,则两圆相内切F1,F2,M三点共线 ,点 M 的轨迹是两条射线.
非零常数等于|F1F2|时
若|AB|>|F1F2|且点 P 在线段 AB 外运动时,则两圆位置关系为内含无交点,即满足条件的点M 不存在.
非零常数大于|F1F2|时
一般地,我们把平面内与两个定点 F1,F2 的距离之差的绝对值等于非零常数(小于|F1F2 |)的点的轨迹叫双曲线.
求曲线方程的步骤:(类比椭圆)
以 F1,F2所在的直线为 x 轴,线段 F1F2 的垂直平分线为y轴,如图建立平面直角坐标系Oxy.
设M(x , y),则 F1(-c,0),F2( c,0).
|MF1|-|MF2|=±2a.
建
化
设
限
代
如何化简呢?(类比椭圆)
x
y
O
F1
F2
焦点在 x 轴的双曲线
F1(-c,0),F2( c,0)
移项
平方
整理
平方
化
类比椭圆
x
y
移项平方法
O
焦点在 x 轴
焦点在 y 轴
F1
F2
焦点在 y 轴的双曲线
F1( 0,-c ),F2( 0,c )
类比椭圆
x2 , y2 的系数哪一个为正,焦点在哪一个轴上.
双曲线的标准方程
x
y
O
F1
F2
x
y
O
F1
F2
焦点在 x 轴
焦点在 y 轴
大小不确定
椭圆 双曲线 定 义 方 程
焦 点
a,b,c的关系 c2 =a2 + b2,
a >0,b >0,但a不一定大于b.
a2 =b2 + c2,
a > b >0.
||MF1|-|MF2||=2a
|MF1|+|MF2|= 2a
F(±c,0)
F(0,±c)
F(±c,0)
F(0,±c)
双曲线的标准方程与椭圆的标准方程有何区别与联系
对比总结
例1 已知双曲线的两个焦点分别为 F1(-5,0), F2(5,0),双曲线上一点 P 与 F1,F2 距离差的绝对值等于 6,求双曲线的标准方程.
典例探究
解:已知双曲线的两个焦点分别为F1(-5,0),F2(5,0).
所以焦点在 x 轴上,且 c = 5.
因为双曲线上一点 P 与 F1,F2 距离差的绝对值等于6,所以 a=3.
由 b2= c2- a2得 b=4.
分析: 由声速及在 A 地听到炮弹爆炸声比在 B 地晚 2 s ,可知A 地与爆炸点的距离比 B 地与爆炸点的距离远 680 m.且 |AB|=800 m > 680 m,
所以爆炸点的轨迹是以 A,B为焦点的双曲线在靠近 B处的一支上.
例2 已知 A , B两地相距 800 m, 在 A 地听到炮弹爆炸声比在 B 地晚 2 s, 且声速为 340 m/s,求炮弹爆炸点的轨迹方程.
解:如图所示,以 A,B所在直线为 x 轴,线段 AB 中垂线为 y 轴建立平面直角坐标系 Oxy .
设爆炸点 P 的坐标为 (x,y),则
可知 2a=680,2c=800,即a=340,c=400.
x
y
|PA|-|PB|=340×2=680<|AB|=800.
由b2=c2-a2得 b2=44 400.
因为 |PA|-|PB|>0所以点P的轨迹是双曲线的右支,因此 x≥340.
O
利用两个不同观测点 A,B 测得同一点 P 发出信号的时间差,可以确定点 P 所在双曲线的方程.
如果再增设一个观测点 C,利用 B,C(或 A,C)两处测得的点 P 发出信号的时间差,就可以确定点 P 所在另一双曲线方程,解这两个方程组成的方程组,就能确定点 P 的位置,这是双曲线的一个重要应用.
1. 本节课你学习了哪些知识和思想方法?
2. 同样都是圆锥曲线,双曲线和椭圆有哪些区别与联系
3. 类比椭圆,在学习了双曲线定义及方程以后,我们需要进一步研究双曲线的哪些方面的知识呢?
基本思路:曲线的背景——定义——方程——性质——应用
3.2.1双曲线及其标准方程
学习目标
1.了解双曲线的实际背景,经历从具体情境中抽象出双曲线的过程,双曲线标准方程的推导过程.
2.掌握双曲线的定义,标准方程及几何图形.(重点)
3.通过双曲线概念的引入和双曲线方程的推导,提高用坐标法解决几何问题的能力.(难点)
情境一:我们的人民海军日夜守护着海疆的安全. 某天同时段内,在 A,B两个海岛上听到了炮弹爆炸声. 已知 A,B 两地相距 800 m. 在A地听到炮弹爆炸声比在 B 地晚 2 s,且声速为 340 m/s,如何确定爆炸点的位置?
A
B
椭圆
双曲线
抛物线
情境二
在本章刚开始的时候,我们已经知道椭圆、双曲线、抛物线统称为圆锥曲线,他们都可以由平面截双锥模型而获得,可见椭圆和双曲线有着内在的联系,那么他们的定义和作图过程是否也有类似的联系和相似之处呢?
圆锥曲线的形成
如图,在直线 l 上取两个定点 A,B,P 是直线 l 上的动点 . 在平面内,取定点 F1,F2, 以点 F1为圆心 、线段PA 为半径作圆,再以 F2 为圆心、线段 PB 为半径作圆.
圆 F1半径 r1 = | PA|,圆 F2半径 r2 = |PB|,圆心距 d = |F1F2|
l
调整 F1,F2 两点的距离,随着点 P 在直线 l 上滑动,两圆的位置和大小关系也随之改变.
当两圆相交时,交点的轨迹 M 会出现哪些图形?
圆 F1半径 r1 = | PA|,圆 F2半径 r2 = |PB|,圆心距 d = |F1F2|
l
圆 F1半径 r1 = | PA|,圆 F2半径 r2 = |PB|,圆心距 d = |F1F2|
l
在变化过程中出现了哪些类型的曲线呢?
我们知道,当点 P 在线段 AB 上运动时,如果
||PA|-|PB||<|F1F2|<|AB|,
那么两圆相交,交点M满足:
|MF1|+|MF2|=|AB|>|F1F2|.
结合椭圆的定义可知:
两圆的交点 M 的轨迹是以 F1,F2 为焦点,以线段 AB 的长为长轴长的椭圆.
r1 +r2 =|AB|(定值)
l
①当 M 靠近定点 F1时,
|MF2|-|MF1|=|AB|
轨迹是一支曲线
当点 P在线段 AB 外运动时,如果|AB|<|F1F2|<|PA|+|PB|,
那么两圆相交,交点 M 满足什么特点呢?
②当M靠近定点F2时,
|MF1|-|MF2|=|AB|
轨迹是另一支曲线.
当点 P在线段 AB 外运动时,如果|AB|<|F1F2|<|PA|+|PB|,
那么两圆相交,交点 M 满足什么特点呢?
综上,交点 M 满足:
||MF1|-|MF2||=|AB|
(|AB|<|F1F2|)
其图像是两支曲线.
我们称之为双曲线.
双曲线的定义
一般地,我们把平面内与两个定点 F1,F2 的距离之差的绝对值等于非零常数(小于|F1F2 |)的点的轨迹叫双曲线(hyperbola).
距离之差的绝对值
非零常数
小于|F1F2|
记为2c
①这两个定点叫做双曲线的焦点.
②两焦点之间的距离叫做双曲线的焦距.
记为2a
符号表示:{ M | ||MF1|-|MF2|| = 2a < |F1F2| =2c }
若 A,B重合
则 |MF1|=|MF2|,点 M在线段 F1F2 的垂直平分线上,即点 M 的轨迹是线段 F1F2的垂直平分线 .
常数等于 0 时
若|AB|=|F1F2|且点 P在线段 AB 外运动,则两圆相内切F1,F2,M三点共线 ,点 M 的轨迹是两条射线.
非零常数等于|F1F2|时
若|AB|>|F1F2|且点 P 在线段 AB 外运动时,则两圆位置关系为内含无交点,即满足条件的点M 不存在.
非零常数大于|F1F2|时
一般地,我们把平面内与两个定点 F1,F2 的距离之差的绝对值等于非零常数(小于|F1F2 |)的点的轨迹叫双曲线.
求曲线方程的步骤:(类比椭圆)
以 F1,F2所在的直线为 x 轴,线段 F1F2 的垂直平分线为y轴,如图建立平面直角坐标系Oxy.
设M(x , y),则 F1(-c,0),F2( c,0).
|MF1|-|MF2|=±2a.
建
化
设
限
代
如何化简呢?(类比椭圆)
x
y
O
F1
F2
焦点在 x 轴的双曲线
F1(-c,0),F2( c,0)
移项
平方
整理
平方
化
类比椭圆
x
y
移项平方法
O
焦点在 x 轴
焦点在 y 轴
F1
F2
焦点在 y 轴的双曲线
F1( 0,-c ),F2( 0,c )
类比椭圆
x2 , y2 的系数哪一个为正,焦点在哪一个轴上.
双曲线的标准方程
x
y
O
F1
F2
x
y
O
F1
F2
焦点在 x 轴
焦点在 y 轴
大小不确定
椭圆 双曲线 定 义 方 程
焦 点
a,b,c的关系 c2 =a2 + b2,
a >0,b >0,但a不一定大于b.
a2 =b2 + c2,
a > b >0.
||MF1|-|MF2||=2a
|MF1|+|MF2|= 2a
F(±c,0)
F(0,±c)
F(±c,0)
F(0,±c)
双曲线的标准方程与椭圆的标准方程有何区别与联系
对比总结
例1 已知双曲线的两个焦点分别为 F1(-5,0), F2(5,0),双曲线上一点 P 与 F1,F2 距离差的绝对值等于 6,求双曲线的标准方程.
典例探究
解:已知双曲线的两个焦点分别为F1(-5,0),F2(5,0).
所以焦点在 x 轴上,且 c = 5.
因为双曲线上一点 P 与 F1,F2 距离差的绝对值等于6,所以 a=3.
由 b2= c2- a2得 b=4.
分析: 由声速及在 A 地听到炮弹爆炸声比在 B 地晚 2 s ,可知A 地与爆炸点的距离比 B 地与爆炸点的距离远 680 m.且 |AB|=800 m > 680 m,
所以爆炸点的轨迹是以 A,B为焦点的双曲线在靠近 B处的一支上.
例2 已知 A , B两地相距 800 m, 在 A 地听到炮弹爆炸声比在 B 地晚 2 s, 且声速为 340 m/s,求炮弹爆炸点的轨迹方程.
解:如图所示,以 A,B所在直线为 x 轴,线段 AB 中垂线为 y 轴建立平面直角坐标系 Oxy .
设爆炸点 P 的坐标为 (x,y),则
可知 2a=680,2c=800,即a=340,c=400.
x
y
|PA|-|PB|=340×2=680<|AB|=800.
由b2=c2-a2得 b2=44 400.
因为 |PA|-|PB|>0所以点P的轨迹是双曲线的右支,因此 x≥340.
O
利用两个不同观测点 A,B 测得同一点 P 发出信号的时间差,可以确定点 P 所在双曲线的方程.
如果再增设一个观测点 C,利用 B,C(或 A,C)两处测得的点 P 发出信号的时间差,就可以确定点 P 所在另一双曲线方程,解这两个方程组成的方程组,就能确定点 P 的位置,这是双曲线的一个重要应用.
1. 本节课你学习了哪些知识和思想方法?
2. 同样都是圆锥曲线,双曲线和椭圆有哪些区别与联系
3. 类比椭圆,在学习了双曲线定义及方程以后,我们需要进一步研究双曲线的哪些方面的知识呢?
基本思路:曲线的背景——定义——方程——性质——应用
