第28章锐角三角形 单元测试(含答案)2024-2025学年数学人教版九年级下册
文档属性
| 名称 | 第28章锐角三角形 单元测试(含答案)2024-2025学年数学人教版九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 367.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-21 00:00:00 | ||
图片预览


文档简介
第28章锐角三角形
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在中,,若,,则等于
A. B. C. D.
2.在中,,如果,,那么AC的长是
A. B. C. D.
3.在中,,,则的值为( )
A. B. C. D.
4.如图,一棵树在一次强台风中,从离地面5m处折断,倒下的部分与地面成角,如图所示,这棵树在折断前的高度是
A. 10m B. 5m C. 15m D. 20m
5.一个钢球沿坡角的斜坡向上滚动了5米,此时钢球距地面的高度是( )
A. 米 B. 米 C. 米 D. 5米
6.如图,AB是圆锥的母线,BC为底面直径,已知,圆锥的侧面积为,则的值为 ( )
A. B. C. D.
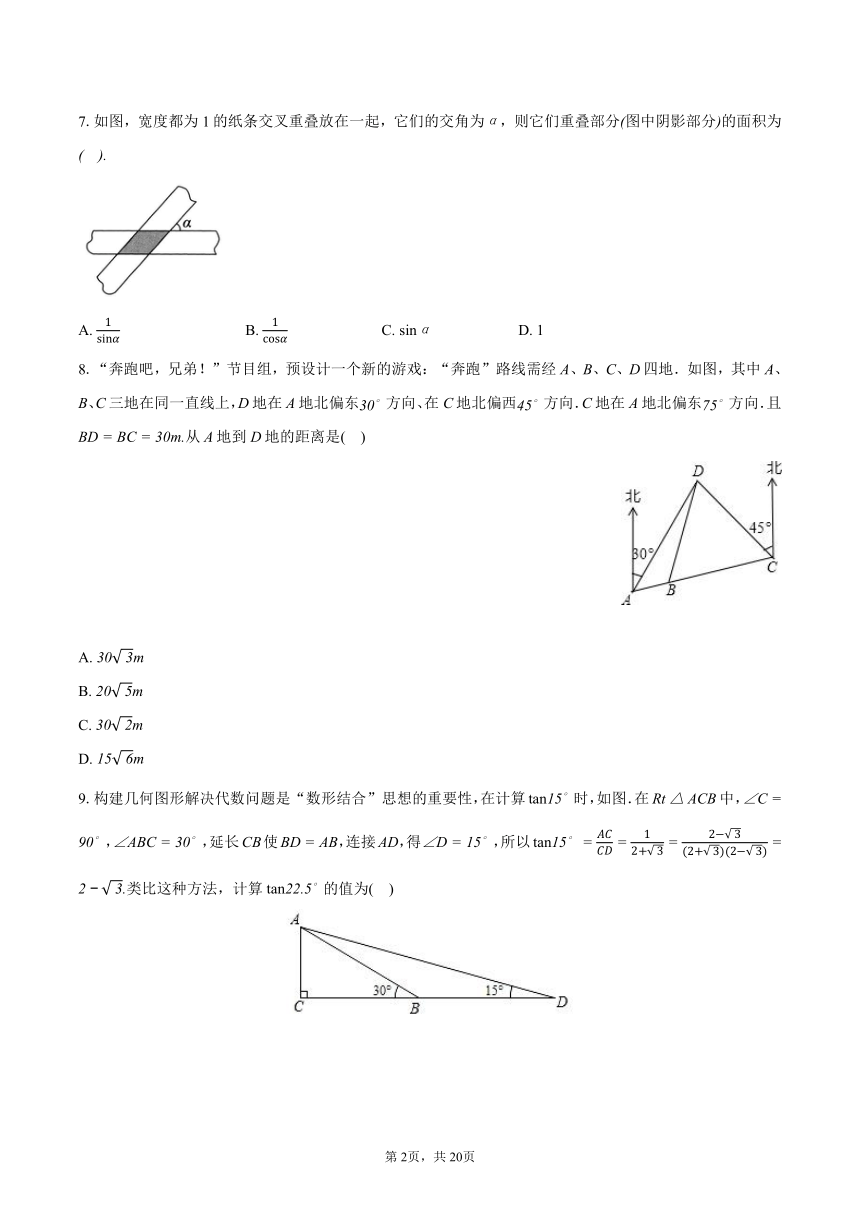
7.如图,宽度都为1的纸条交叉重叠放在一起,它们的交角为,则它们重叠部分图中阴影部分的面积为
A. B. C. D. 1
8.“奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东方向、在C地北偏西方向.C地在A地北偏东方向.且从A地到D地的距离是( )
A.
B.
C.
D.
9.构建几何图形解决代数问题是“数形结合”思想的重要性,在计算时,如图.在中,,,延长CB使,连接AD,得,所以类比这种方法,计算的值为( )
A. B. C. D.
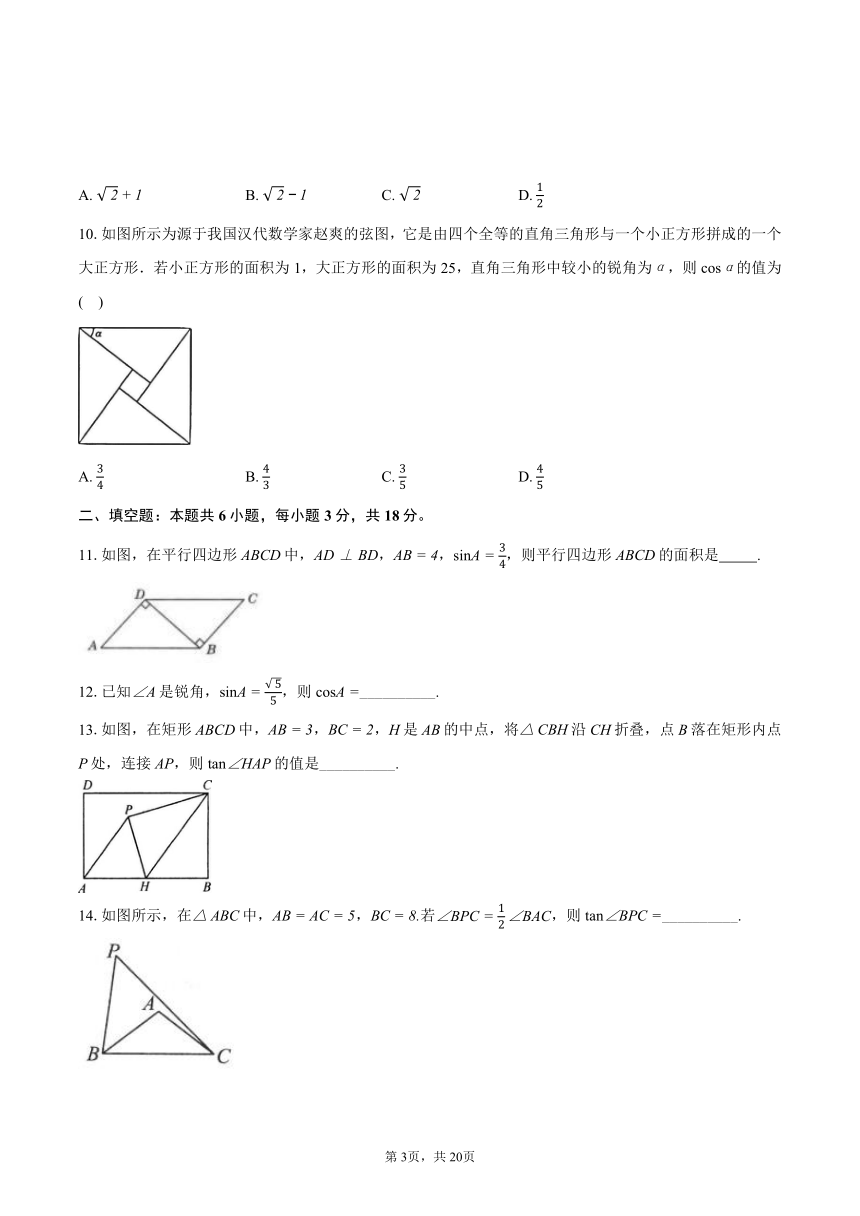
10.如图所示为源于我国汉代数学家赵爽的弦图,它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为,则的值为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.如图,在平行四边形ABCD中,,,,则平行四边形ABCD的面积是 .
12.已知是锐角,,则__________.
13.如图,在矩形ABCD中,,,H是AB的中点,将沿CH折叠,点B落在矩形内点P处,连接AP,则的值是__________.
14.如图所示,在中,,若,则__________.
15.如图,有一张面积为10的纸片,,把它剪两刀拼成一个矩形如图虚线所示,无缝隙、无重叠,且矩形的一边与AB平行,所拼得矩形的周长为13,则的值为__________.
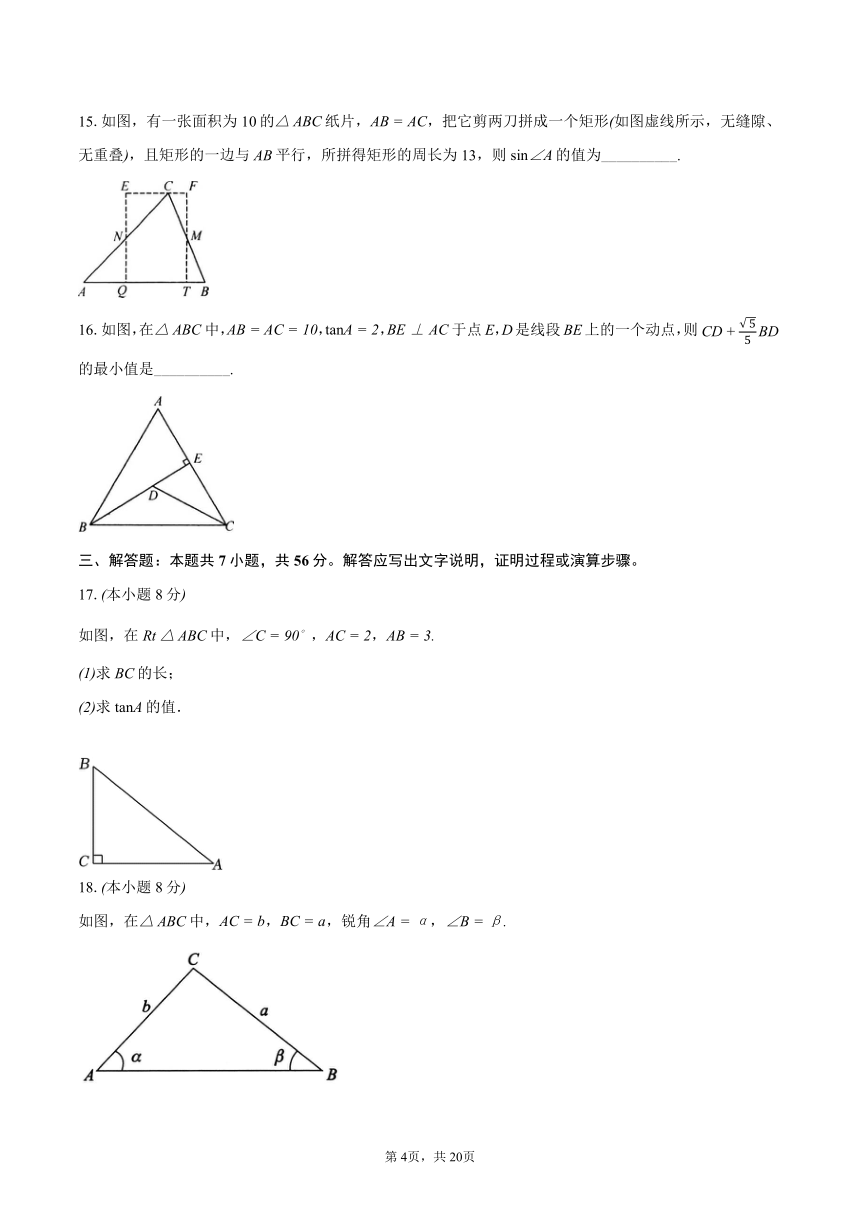
16.如图,在中,,,于点E,D是线段BE上的一个动点,则的最小值是__________.
三、解答题:本题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤。
17.本小题8分
如图,在中,,,
求BC的长;
求的值.
18.本小题8分
如图,在中,,,锐角,
求AB的长;
求证:
19.本小题8分
如图,在中,,于点
已知,
求AD的长;
求AB的长.
20.本小题8分
如图,A是的直径CD延长线上的一点,点B在上,
求证:AB是的切线;
若,求AC的长.
21.本小题8分
楼房AB后有一假山,其斜坡CD的坡度,山坡坡面上点E处有一个休息亭.如图所示,小红从楼房顶A处测得点E的俯角为,测得斜坡的点C处与楼房的水平距离,与亭子的距离求楼房AB的高度.
22.本小题8分
如图,在中,,BO平分,交AC于点O,以点O为圆心,OC长为半径画
求证:AB是的切线;
若,,求的半径.
23.本小题8分
已知正方形ABCD,将线段BA绕点B旋转,得到线段BE,连接EA,
如图1,当点E在正方形ABCD的内部时,若BE平分,,则______,四边形ABCE的面积为______;
当点E在正方形ABCD的外部时,
①在图2中依题意补全图形,并求的度数;
②作的平分线BF交EC于点G,交EA的延长线于点F,连接用等式表示线段AE,FB,FC之间的数量关系,并证明.
答案和解析
1.【答案】C
【解析】【分析】
此题考查的是锐角三角函数的定义,解答此类题目的关键是画出图形便可直观解答.根据三角函数的定义求解.
【解答】
解:中,,,,
故选
2.【答案】D
【解析】解:如图:
在中,
故选:
3.【答案】D
【解析】略
4.【答案】C
【解析】解:如图,在中,,,,
,
大树的高度为
故选
5.【答案】A
【解析】见答案.
6.【答案】B
【解析】略
7.【答案】A
【解析】解:如图所示,作,,垂足分别为E、F,
依题意,有,
根据已知得,
所以≌,
,
则四边形ABCD是菱形.
在中,
所以,
故选
如图所示,过A作,,垂足分别为E、F,依题意,有,可证得然后可证得≌,得,则四边形ABCD是菱形.在中,,由此根据菱形的面积公式即可求出其面积.
本题考查了直角三角形的应用,菱形的判定与性质.
8.【答案】D
【解析】【分析】
过点D作DH垂直于AC,垂足为H,求出的度数,判断出是等边三角形,再利用三角函数求出DH的长,从而得到AD的长.
本题考查了解直角三角形的应用--方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.
【解答】
解:过点D作DH垂直于AC,垂足为H,
由题意可知,
,
是等边三角形,
,,
,
答:从A地到D地的距离是
故选:
9.【答案】B
【解析】【分析】
作,使,,延长CB到D,使,连接AD,根据构造的直角三角形,设,再用x表示出CD,即可求出的值.
本题考查解直角三角形,解题的关键是根据阅读构造含的直角三角形,再作辅助线得到的直角三角形.
【解答】
解:作,使,,延长CB到D,使,连接AD,
则,
,
设,则:,,,
,
故选:
10.【答案】D
【解析】略
11.【答案】
【解析】略
12.【答案】
【解析】【分析】
本题主要考查了锐角三角函数的定义,勾股定理,解答此题的关键是构造出直角三角形.根据题意构造出直角三角形,根据直角三角形中锐角三角函数的定义解答.
【解答】
解:为锐角,且,以为锐角作直角三角形,
,
设,则,
根据勾股定理可得:,
故答案为
13.【答案】
【解析】解:连接PB交CH于点E,由折叠可得CH垂直平分BP,
为BP的中点,又为AB的中点,是的中位线,
,,
又在中,,
14.【答案】
【解析】【分析】
本题考查的是勾股定理,锐角三角函数的定义,解直角三角形有关知识点.
作于H,如图,根据等腰三角形的性质得,,而,则,在中利用勾股定理计算出,然后根据正切的定义求解.
【解答】
解:作于H,如图,
,AH平分,
,
,
,
在中,
,,
,
,
故答案为
15.【答案】或
【解析】解:由题意及观察拼图可知,
矩形的边,边,
设,,则,,
解得,或,,
或
16.【答案】
【解析】解:过点D,C分别作于点H,于点
,,
,
设,,
则有,
,
或舍去,
,
,,,
等腰三角形两腰上的高相等,
,,
,
,,
,,
的最小值为
17.【答案】解:在中,,,,
;
在中,,,,
【解析】见答案
18.【答案】解:过C作于D,
由题意得,,,
即,
由可得,
变形得
【解析】本题主要考查了解直角三角形,熟练掌握锐角三角函数的定义是解题的关键.
根据题意解直角三角形方法,先求得,,即可求得AB的长;
先由解直角三角形方法求得进行变形求值即得到所求结论.
19.【答案】解:,,,
,
,
,
在中,,
【解析】本题考查解直角三角形,熟练掌握锐角三角函数的定义是解题的关键.
直接根据锐角三角函数的概念进行求解;
根据等角的余角相等,得,从而再根据的正弦值,即可求得AB的长.
20.【答案】证明:如图,
连接OB,
,
,
,
,
,
点B在上,
是的切线;
解:如图2,
连接BD,
是的直径,
,
,,
,
,
,
,
,
【解析】本题考查了圆周角定理及其推论,切线的判定,等腰三角形的判定,解直角三角形等知识,解决问题的关键是熟练掌握有关基础知识.
连接OB,可证明,进一步得出结论;
可连接BD,解直角三角形BCD求得BD和CD,进而判定ABD是等腰三角形,进一步得出结果.
本题考查了圆周角定理及其推论,切线的判定,等腰三角形的判定,解直角三角形等知识,解决问题的关键是熟练掌握有关基础知识.
21.【答案】解:过点E作的延长线于F,于点H,
在中,,
,
米,米,
米,米,
在中,,
米,
米.
答:楼房AB的高为米.
【解析】本题考查了解直角三角形的应用,涉及仰角俯角及坡度坡角的知识,构造直角三角形是解题关键.
过点E作的延长线于F,于点H,根据米,坡度为:,分别求出EF、CF的长度,在中求出AH,继而可得楼房AB的高.
22.【答案】证明.如图所示,过点 O作于点
,
平分,,,
,
是的切线.
解:
设,结合得≌ ,
则
,,
∽,
,
在中,,
解得或舍去,
的半径为
【解析】本题考查了切线的判定与性质,勾股定理,相似三角形的判定与性质,锐角三角函数的定义,属于中档题.
过点O作于点H,由,得,根据角平分线的性质得,由此得结论;
设,可求得,根据相似三角形的判定和性质以及勾股定理可得结论.
23.【答案】解:将线段BA绕点B旋转,得到线段BE,
,
,
四边形ABCD是正方形,
,,
平分,
,
,
≌,
,
;
过点A作于点F,如图1,
,
,
,
四边形ABCE的面积,
故答案为:,;
①补全图形如图2,
将线段BA绕点B旋转,得到线段BE,
,,,
,,
;
②
证明:过点B作交FC的延长线于点H,如图3,
,BF平分,
垂直平分EC,
,,
,
,
,
,,
,,
,,
,
,
≌,
,
,
【解析】本题是四边形综合题,考查了旋转的性质,正方形的性质,等腰直角三角形的性质,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题.
由旋转的性质得出,证明≌,由全等三角形的性质得出,可求出,过点A作于点F,求出的面积,则可得出答案;
①由题意可画出图形,由旋转的性质及等腰三角形的性质可得出答案;
②过点B作交FC的延长线于点H,证明≌,由全等三角形的性质得出,由等腰直角三角形的性质可得出结论.
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在中,,若,,则等于
A. B. C. D.
2.在中,,如果,,那么AC的长是
A. B. C. D.
3.在中,,,则的值为( )
A. B. C. D.
4.如图,一棵树在一次强台风中,从离地面5m处折断,倒下的部分与地面成角,如图所示,这棵树在折断前的高度是
A. 10m B. 5m C. 15m D. 20m
5.一个钢球沿坡角的斜坡向上滚动了5米,此时钢球距地面的高度是( )
A. 米 B. 米 C. 米 D. 5米
6.如图,AB是圆锥的母线,BC为底面直径,已知,圆锥的侧面积为,则的值为 ( )
A. B. C. D.
7.如图,宽度都为1的纸条交叉重叠放在一起,它们的交角为,则它们重叠部分图中阴影部分的面积为
A. B. C. D. 1
8.“奔跑吧,兄弟!”节目组,预设计一个新的游戏:“奔跑”路线需经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东方向、在C地北偏西方向.C地在A地北偏东方向.且从A地到D地的距离是( )
A.
B.
C.
D.
9.构建几何图形解决代数问题是“数形结合”思想的重要性,在计算时,如图.在中,,,延长CB使,连接AD,得,所以类比这种方法,计算的值为( )
A. B. C. D.
10.如图所示为源于我国汉代数学家赵爽的弦图,它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形.若小正方形的面积为1,大正方形的面积为25,直角三角形中较小的锐角为,则的值为( )
A. B. C. D.
二、填空题:本题共6小题,每小题3分,共18分。
11.如图,在平行四边形ABCD中,,,,则平行四边形ABCD的面积是 .
12.已知是锐角,,则__________.
13.如图,在矩形ABCD中,,,H是AB的中点,将沿CH折叠,点B落在矩形内点P处,连接AP,则的值是__________.
14.如图所示,在中,,若,则__________.
15.如图,有一张面积为10的纸片,,把它剪两刀拼成一个矩形如图虚线所示,无缝隙、无重叠,且矩形的一边与AB平行,所拼得矩形的周长为13,则的值为__________.
16.如图,在中,,,于点E,D是线段BE上的一个动点,则的最小值是__________.
三、解答题:本题共7小题,共56分。解答应写出文字说明,证明过程或演算步骤。
17.本小题8分
如图,在中,,,
求BC的长;
求的值.
18.本小题8分
如图,在中,,,锐角,
求AB的长;
求证:
19.本小题8分
如图,在中,,于点
已知,
求AD的长;
求AB的长.
20.本小题8分
如图,A是的直径CD延长线上的一点,点B在上,
求证:AB是的切线;
若,求AC的长.
21.本小题8分
楼房AB后有一假山,其斜坡CD的坡度,山坡坡面上点E处有一个休息亭.如图所示,小红从楼房顶A处测得点E的俯角为,测得斜坡的点C处与楼房的水平距离,与亭子的距离求楼房AB的高度.
22.本小题8分
如图,在中,,BO平分,交AC于点O,以点O为圆心,OC长为半径画
求证:AB是的切线;
若,,求的半径.
23.本小题8分
已知正方形ABCD,将线段BA绕点B旋转,得到线段BE,连接EA,
如图1,当点E在正方形ABCD的内部时,若BE平分,,则______,四边形ABCE的面积为______;
当点E在正方形ABCD的外部时,
①在图2中依题意补全图形,并求的度数;
②作的平分线BF交EC于点G,交EA的延长线于点F,连接用等式表示线段AE,FB,FC之间的数量关系,并证明.
答案和解析
1.【答案】C
【解析】【分析】
此题考查的是锐角三角函数的定义,解答此类题目的关键是画出图形便可直观解答.根据三角函数的定义求解.
【解答】
解:中,,,,
故选
2.【答案】D
【解析】解:如图:
在中,
故选:
3.【答案】D
【解析】略
4.【答案】C
【解析】解:如图,在中,,,,
,
大树的高度为
故选
5.【答案】A
【解析】见答案.
6.【答案】B
【解析】略
7.【答案】A
【解析】解:如图所示,作,,垂足分别为E、F,
依题意,有,
根据已知得,
所以≌,
,
则四边形ABCD是菱形.
在中,
所以,
故选
如图所示,过A作,,垂足分别为E、F,依题意,有,可证得然后可证得≌,得,则四边形ABCD是菱形.在中,,由此根据菱形的面积公式即可求出其面积.
本题考查了直角三角形的应用,菱形的判定与性质.
8.【答案】D
【解析】【分析】
过点D作DH垂直于AC,垂足为H,求出的度数,判断出是等边三角形,再利用三角函数求出DH的长,从而得到AD的长.
本题考查了解直角三角形的应用--方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.
【解答】
解:过点D作DH垂直于AC,垂足为H,
由题意可知,
,
是等边三角形,
,,
,
答:从A地到D地的距离是
故选:
9.【答案】B
【解析】【分析】
作,使,,延长CB到D,使,连接AD,根据构造的直角三角形,设,再用x表示出CD,即可求出的值.
本题考查解直角三角形,解题的关键是根据阅读构造含的直角三角形,再作辅助线得到的直角三角形.
【解答】
解:作,使,,延长CB到D,使,连接AD,
则,
,
设,则:,,,
,
故选:
10.【答案】D
【解析】略
11.【答案】
【解析】略
12.【答案】
【解析】【分析】
本题主要考查了锐角三角函数的定义,勾股定理,解答此题的关键是构造出直角三角形.根据题意构造出直角三角形,根据直角三角形中锐角三角函数的定义解答.
【解答】
解:为锐角,且,以为锐角作直角三角形,
,
设,则,
根据勾股定理可得:,
故答案为
13.【答案】
【解析】解:连接PB交CH于点E,由折叠可得CH垂直平分BP,
为BP的中点,又为AB的中点,是的中位线,
,,
又在中,,
14.【答案】
【解析】【分析】
本题考查的是勾股定理,锐角三角函数的定义,解直角三角形有关知识点.
作于H,如图,根据等腰三角形的性质得,,而,则,在中利用勾股定理计算出,然后根据正切的定义求解.
【解答】
解:作于H,如图,
,AH平分,
,
,
,
在中,
,,
,
,
故答案为
15.【答案】或
【解析】解:由题意及观察拼图可知,
矩形的边,边,
设,,则,,
解得,或,,
或
16.【答案】
【解析】解:过点D,C分别作于点H,于点
,,
,
设,,
则有,
,
或舍去,
,
,,,
等腰三角形两腰上的高相等,
,,
,
,,
,,
的最小值为
17.【答案】解:在中,,,,
;
在中,,,,
【解析】见答案
18.【答案】解:过C作于D,
由题意得,,,
即,
由可得,
变形得
【解析】本题主要考查了解直角三角形,熟练掌握锐角三角函数的定义是解题的关键.
根据题意解直角三角形方法,先求得,,即可求得AB的长;
先由解直角三角形方法求得进行变形求值即得到所求结论.
19.【答案】解:,,,
,
,
,
在中,,
【解析】本题考查解直角三角形,熟练掌握锐角三角函数的定义是解题的关键.
直接根据锐角三角函数的概念进行求解;
根据等角的余角相等,得,从而再根据的正弦值,即可求得AB的长.
20.【答案】证明:如图,
连接OB,
,
,
,
,
,
点B在上,
是的切线;
解:如图2,
连接BD,
是的直径,
,
,,
,
,
,
,
,
【解析】本题考查了圆周角定理及其推论,切线的判定,等腰三角形的判定,解直角三角形等知识,解决问题的关键是熟练掌握有关基础知识.
连接OB,可证明,进一步得出结论;
可连接BD,解直角三角形BCD求得BD和CD,进而判定ABD是等腰三角形,进一步得出结果.
本题考查了圆周角定理及其推论,切线的判定,等腰三角形的判定,解直角三角形等知识,解决问题的关键是熟练掌握有关基础知识.
21.【答案】解:过点E作的延长线于F,于点H,
在中,,
,
米,米,
米,米,
在中,,
米,
米.
答:楼房AB的高为米.
【解析】本题考查了解直角三角形的应用,涉及仰角俯角及坡度坡角的知识,构造直角三角形是解题关键.
过点E作的延长线于F,于点H,根据米,坡度为:,分别求出EF、CF的长度,在中求出AH,继而可得楼房AB的高.
22.【答案】证明.如图所示,过点 O作于点
,
平分,,,
,
是的切线.
解:
设,结合得≌ ,
则
,,
∽,
,
在中,,
解得或舍去,
的半径为
【解析】本题考查了切线的判定与性质,勾股定理,相似三角形的判定与性质,锐角三角函数的定义,属于中档题.
过点O作于点H,由,得,根据角平分线的性质得,由此得结论;
设,可求得,根据相似三角形的判定和性质以及勾股定理可得结论.
23.【答案】解:将线段BA绕点B旋转,得到线段BE,
,
,
四边形ABCD是正方形,
,,
平分,
,
,
≌,
,
;
过点A作于点F,如图1,
,
,
,
四边形ABCE的面积,
故答案为:,;
①补全图形如图2,
将线段BA绕点B旋转,得到线段BE,
,,,
,,
;
②
证明:过点B作交FC的延长线于点H,如图3,
,BF平分,
垂直平分EC,
,,
,
,
,
,,
,,
,,
,
,
≌,
,
,
【解析】本题是四边形综合题,考查了旋转的性质,正方形的性质,等腰直角三角形的性质,全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题.
由旋转的性质得出,证明≌,由全等三角形的性质得出,可求出,过点A作于点F,求出的面积,则可得出答案;
①由题意可画出图形,由旋转的性质及等腰三角形的性质可得出答案;
②过点B作交FC的延长线于点H,证明≌,由全等三角形的性质得出,由等腰直角三角形的性质可得出结论.
第1页,共1页
