第一章 全等三角形 单元练习(含答案)2024-2025学年数学苏科版八年级上册
文档属性
| 名称 | 第一章 全等三角形 单元练习(含答案)2024-2025学年数学苏科版八年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 432.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-21 14:33:11 | ||
图片预览




文档简介
第一章全等三角形
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列选项中的图形与如图全等的是( )
A. B. C. D.
2.给出下列四个条件:,,,,从中任选三个条件,能使≌的共有 ( )
A. 1组 B. 2组 C. 3组 D. 4组
3.如图,在中,,,观察图中尺规作图的痕迹,则的度数为 ( )
A. B. C. D.
4.如图,,,M,N分别为CA,CB的中点,,,则的度数为 ( )
A. B. C. D.
5.已知与全等,A,B,C三点的对应点分别为D,E,F三点,且点E在AC上,B,F,C,D四点共线,如图所示.若,,则下列结论正确的是 ( )
A. , B. ,
C. , D. ,
6.如图,在中,,,D是AC的中点,,交BD的延长线于点E,交BA的延长线于点若,则的面积是 ( )
A. 40 B. 46 C. 48 D. 50
7.如图,在中,,,,垂足为R,,垂足为有下列三个结论:①;②;③≌下列说法正确的是 ( )
A. ①②③ B. ①② C. ① D. ①③
8.如图,在中,的平分线交AC于点若,,则的度数为 ( )
A. B. C. D.
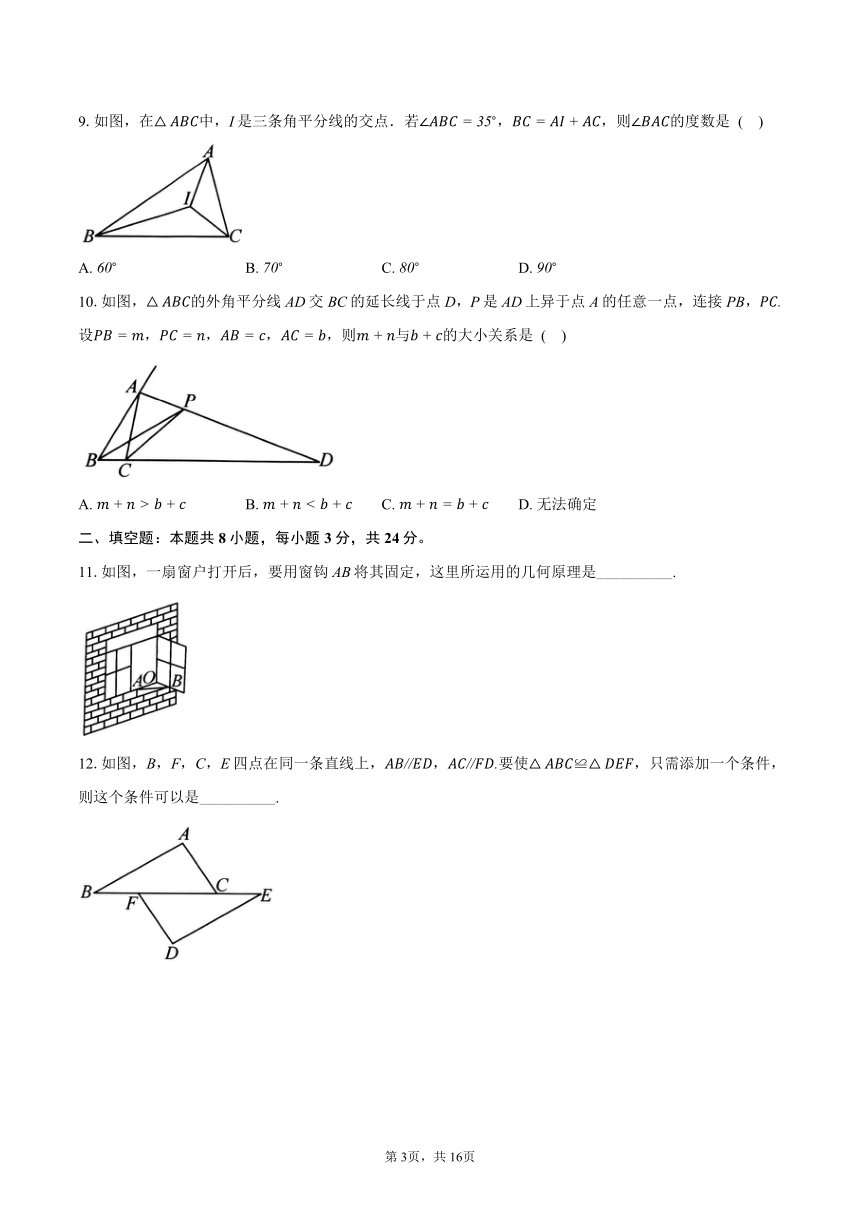
9.如图,在中,I是三条角平分线的交点.若,,则的度数是 ( )
A. B. C. D.
10.如图,的外角平分线AD交BC的延长线于点D,P是AD上异于点A的任意一点,连接PB,设,,,,则与的大小关系是 ( )
A. B. C. D. 无法确定
二、填空题:本题共8小题,每小题3分,共24分。
11.如图,一扇窗户打开后,要用窗钩AB将其固定,这里所运用的几何原理是__________.
12.如图,B,F,C,E四点在同一条直线上,,要使≌,只需添加一个条件,则这个条件可以是__________.
13.如图,以的顶点A为圆心,BC的长为半径作弧;再以顶点C为圆心,AB的长为半径作弧,两弧交于点D,连接AD,若,则的度数为__________.
14.如图,点O在一个直角三角尺ABC上其中,于点M,于点若,则__________
15.如图,点A在DE上,点F在AB上,且,,,则AB的长为__________.
16.如图,在中,,按以下步骤作图:①以点B为圆心,任意长为半径作弧,分别交BA,BC于M,N两点;②分别以M,N两点为圆心,以大于的长为半径作弧,两弧相交于点P;③作射线BP,交边AC于点若,,,则线段CD的长为__________.
17.如图,在长方形ABCD中,,,点P从点B出发,以的速度沿边BC向点C运动,到达点C停止,同时,点Q从点C出发,以的速度沿边CD向点D运动,到达点D停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当v的值为__________时,与全等.
18.如图,,,B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM的两侧作等腰直角三角形OBF和等腰直角三角形ABE,连接EF交OM于点P,当点B在射线OM上移动时,线段PB的长为__________.
三、解答题:本题共8小题,共64分。解答应写出文字说明,证明过程或演算步骤。
19.本小题8分
如图,AB交CD于点O,在与中,有下列三个条件:①;②;③请你在上述三个条件中选择两个为条件,另一个作为这两个条件推出来的结论,并证明你的结论要求写出一种正确的选法
你选的条件为__________、__________,结论为__________填序号;
证明你的结论.
20.本小题8分
如图,将长方形ABCD沿对角线AC折叠,点B的对应点为点E,AE与CD相交于点
求证:≌;
若,求的度数.
21.本小题8分
如图,在中,,,在的顶点A,C处各有一只小蚂蚁,它们同时出发,分别以相同的速度由点A向点B和由点C向点A爬行,经过t s后,它们分别爬行到了D,E两点处,设DC与BE的交点为
求证:≌;
小蚂蚁在爬行过程中,DC与BE所成的的大小有无变化?请说明理由.
22.本小题8分
如图,杨阳同学沿一段笔直的人行道行走,在由A处步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙CD上的社会主义核心价值观标语,其具体信息汇集如下:
已知,,相邻两平行线间的距离相等,AC,BD相交于点O,,垂足为请根据上述信息求宣传墙CD的长度.
23.本小题8分
如图,B,F,C,E是直线l上的四点,且,,
求证:≌;
将沿直线l翻折得到
①用直尺和圆规在图中作出保留作图痕迹,不要求写作法;
②连接,则直线与l的位置关系是________.
24.本小题8分
已知一个三角形两条边的长分别是1 cm和2 cm,一个内角为请用无刻度的直尺和圆规完成作图并解答问题.
在图①中画出一个满足题中条件的三角形;
你是否还能画出既满足题中条件,又与中所画的三角形不全等的三角形?若能,在图②中画出所有这样的三角形;若不能,请说明理由;
如果将题中条件改为“三角形两条边的长分别是3 cm和4 cm,一个内角为”,那么满足这一条件,且彼此不全等的三角形共有__________个.在你画的图中标出已知角的度数和已知边的长度,不写作法,但要保留作图痕迹
25.本小题8分
在中,,,直线MN经过点C,且于点D,于点
当直线MN绕点C旋转到图①的位置时,请你探究线段DE,AD,BE之间的数量关系,并加以证明;
当直线MN绕点C旋转到图②的位置时,你在中得到的结论是否发生变化?请写出你的猜想,并加以证明;
当直线MN绕点C旋转到图③的位置时,你在中得到的结论是否发生变化?请写出你的猜想,并加以证明.
26.本小题8分
已知在五边形ABCDE中,,,连接AC,AD,且
如图①,若求证:;
如图②,在的条件下,连接BE,分别交AC,AD于M,N两点.若,AF为中边BE上的中线.求证:;
如图③,在的条件下,若,,则五边形ABCDE的面积为__________.
答案和解析
1.【答案】B
【解析】略
2.【答案】C
【解析】【分析】
此题考查了全等三角形的判定,掌握全等三角形的判定方法是关键,要使≌的条件必须满足SSS、SAS、ASA、AAS,可据此进行判断.
【解答】
解:第①组,,,满足AAS,能证明≌;
第②组,,满足SAS,能证明≌;
第③组,,满足ASA,能证明≌;
所以有3组能证明≌
故选
3.【答案】B
【解析】【分析】
本题考查了作图-基本作图、等腰三角形的性质,解决本题的关键是掌握等腰三角形的性质.根据等腰三角形的性质可得的度数,由邻补角关系求出度数,观察作图过程可得CE平分,利用角平分线定义而可得的度数.
【解答】
解:,,
,
,
观察作图过程可知:
CE平分,
,
的度数为,
故选:
4.【答案】C
【解析】略
5.【答案】B
【解析】略
6.【答案】C
【解析】略
7.【答案】B
【解析】略
8.【答案】D
【解析】延长BA至点E,使,连接则因为,所以又BD平分,所以在和中, 所以≌所以又,所以又,所以为等腰三角形.所以又,所以又,所以
9.【答案】B
【解析】【分析】
本题考查了全等三角形的判定与性质,三角形的外角性质,等腰三角形的判定与性质等内容.
在BC上截取,连接根据I是三条角平分线的交点,证得≌进而得,可得答案.
【解答】
解:在BC上截取,连接
因为,的平分线交于点I,
所以,
在和中,
所以≌
所以,
因为,,
所以,即
所以是等腰三角形
所以
所以
因为BI平分,所以
所以,即
所以
因为,
所以
10.【答案】A
【解析】在BA的延长线上取点E,使,连接因为AD是的外角平分线,所以在和中, 所以≌所以在中,又,所以,即因为,,,,所以
11.【答案】三角形的稳定性
【解析】略
12.【答案】答案不唯一,如:
【解析】略
13.【答案】
【解析】略
14.【答案】15
【解析】略
15.【答案】3
【解析】略
16.【答案】3
【解析】略
17.【答案】2或
【解析】因为四边形ABCD是长方形,,,所以,,所以与全等可分为≌或≌两种情况.当≌时,,所以所以又点P运动的速度为,所以点P运动的时间为此时,所以 ;当≌时,, .所以点P的运动时间为所以 .综上,当v的值为2或 时,与全等.
18.【答案】2
【解析】过点E作交OM于点所以所以又,所以又和都是等腰直角三角形,所以,,又,所以,即在和中, 所以≌所以,,即又,所以,即在和中, 所以≌所以又,所以
HB .又,所以,即
19.【答案】【小题1】
①
③
②
【小题2】
在和中, 所以≌所以
【解析】答案不唯一
略
20.【答案】【小题1】由题意,得,由折叠的性质,得,,,所以,又,所以≌
【小题2】
由,得,,所以, .又,,所以,即所以
【解析】见答案
见答案
21.【答案】【小题1】由题意,得在和中, 所以≌
【小题2】的大小无变化.理由如下:由,得≌,所以因为,,所以因为,所以因为,所以所以的大小无变化.
【解析】略
略
22.【答案】因为,所以因为,所以所以,即因为相邻两平行线间的距离相等,所以在和中, 所以≌所以又,所以则宣传墙CD的长度为
【解析】略
23.【答案】【小题1】因为,所以又,所以,即在和中, 所以≌
【小题2】
①如图,即为所作.
②平行
【解析】略
略
24.【答案】【小题1】
如图①:
【小题2】
能.如图②:
【小题3】
4
【解析】略
略
当已知角为两条边的夹角时,可画出1个满足条件的三角形;当3 cm长的边作为角的对边时,可画出2个满足条件的三角形;当4 cm长的边作为角的对边时,可画出1个满足条件的三角形.则符合条件的三角形共有个
25.【答案】【小题1】证明如下:因为,,所以因为,,所以所以所以在和中, 所以≌所以,所以
【小题2】发生变化,证明如下:因为,所以因为,,所以所以所以在和中, 所以≌所以,所以
【小题3】发生变化,证明如下:因为,所以因为,,所以所以所以在和中, 所以≌所以,所以
【解析】略
略
略
26.【答案】【小题1】
因为,所以又,所以又,,所以所以
【小题2】
延长AF,BC交于点G,设AG交CD于点P,如图.由,得≌,,,所以,又,所以,即所以所以又AF为中边BE上的中线,所以又,所以≌所以,即又,所以≌所以因为,所以,即所以又,所以所以
【小题3】
42
【解析】略
略
由,得,,,所以又,所以,即又,所以四边形ACDE是直角梯形.又,,,所以,所以 , .所以
第1页,共1页
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下列选项中的图形与如图全等的是( )
A. B. C. D.
2.给出下列四个条件:,,,,从中任选三个条件,能使≌的共有 ( )
A. 1组 B. 2组 C. 3组 D. 4组
3.如图,在中,,,观察图中尺规作图的痕迹,则的度数为 ( )
A. B. C. D.
4.如图,,,M,N分别为CA,CB的中点,,,则的度数为 ( )
A. B. C. D.
5.已知与全等,A,B,C三点的对应点分别为D,E,F三点,且点E在AC上,B,F,C,D四点共线,如图所示.若,,则下列结论正确的是 ( )
A. , B. ,
C. , D. ,
6.如图,在中,,,D是AC的中点,,交BD的延长线于点E,交BA的延长线于点若,则的面积是 ( )
A. 40 B. 46 C. 48 D. 50
7.如图,在中,,,,垂足为R,,垂足为有下列三个结论:①;②;③≌下列说法正确的是 ( )
A. ①②③ B. ①② C. ① D. ①③
8.如图,在中,的平分线交AC于点若,,则的度数为 ( )
A. B. C. D.
9.如图,在中,I是三条角平分线的交点.若,,则的度数是 ( )
A. B. C. D.
10.如图,的外角平分线AD交BC的延长线于点D,P是AD上异于点A的任意一点,连接PB,设,,,,则与的大小关系是 ( )
A. B. C. D. 无法确定
二、填空题:本题共8小题,每小题3分,共24分。
11.如图,一扇窗户打开后,要用窗钩AB将其固定,这里所运用的几何原理是__________.
12.如图,B,F,C,E四点在同一条直线上,,要使≌,只需添加一个条件,则这个条件可以是__________.
13.如图,以的顶点A为圆心,BC的长为半径作弧;再以顶点C为圆心,AB的长为半径作弧,两弧交于点D,连接AD,若,则的度数为__________.
14.如图,点O在一个直角三角尺ABC上其中,于点M,于点若,则__________
15.如图,点A在DE上,点F在AB上,且,,,则AB的长为__________.
16.如图,在中,,按以下步骤作图:①以点B为圆心,任意长为半径作弧,分别交BA,BC于M,N两点;②分别以M,N两点为圆心,以大于的长为半径作弧,两弧相交于点P;③作射线BP,交边AC于点若,,,则线段CD的长为__________.
17.如图,在长方形ABCD中,,,点P从点B出发,以的速度沿边BC向点C运动,到达点C停止,同时,点Q从点C出发,以的速度沿边CD向点D运动,到达点D停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当v的值为__________时,与全等.
18.如图,,,B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM的两侧作等腰直角三角形OBF和等腰直角三角形ABE,连接EF交OM于点P,当点B在射线OM上移动时,线段PB的长为__________.
三、解答题:本题共8小题,共64分。解答应写出文字说明,证明过程或演算步骤。
19.本小题8分
如图,AB交CD于点O,在与中,有下列三个条件:①;②;③请你在上述三个条件中选择两个为条件,另一个作为这两个条件推出来的结论,并证明你的结论要求写出一种正确的选法
你选的条件为__________、__________,结论为__________填序号;
证明你的结论.
20.本小题8分
如图,将长方形ABCD沿对角线AC折叠,点B的对应点为点E,AE与CD相交于点
求证:≌;
若,求的度数.
21.本小题8分
如图,在中,,,在的顶点A,C处各有一只小蚂蚁,它们同时出发,分别以相同的速度由点A向点B和由点C向点A爬行,经过t s后,它们分别爬行到了D,E两点处,设DC与BE的交点为
求证:≌;
小蚂蚁在爬行过程中,DC与BE所成的的大小有无变化?请说明理由.
22.本小题8分
如图,杨阳同学沿一段笔直的人行道行走,在由A处步行到达B处的过程中,通过隔离带的空隙O,刚好浏览完对面人行道宣传墙CD上的社会主义核心价值观标语,其具体信息汇集如下:
已知,,相邻两平行线间的距离相等,AC,BD相交于点O,,垂足为请根据上述信息求宣传墙CD的长度.
23.本小题8分
如图,B,F,C,E是直线l上的四点,且,,
求证:≌;
将沿直线l翻折得到
①用直尺和圆规在图中作出保留作图痕迹,不要求写作法;
②连接,则直线与l的位置关系是________.
24.本小题8分
已知一个三角形两条边的长分别是1 cm和2 cm,一个内角为请用无刻度的直尺和圆规完成作图并解答问题.
在图①中画出一个满足题中条件的三角形;
你是否还能画出既满足题中条件,又与中所画的三角形不全等的三角形?若能,在图②中画出所有这样的三角形;若不能,请说明理由;
如果将题中条件改为“三角形两条边的长分别是3 cm和4 cm,一个内角为”,那么满足这一条件,且彼此不全等的三角形共有__________个.在你画的图中标出已知角的度数和已知边的长度,不写作法,但要保留作图痕迹
25.本小题8分
在中,,,直线MN经过点C,且于点D,于点
当直线MN绕点C旋转到图①的位置时,请你探究线段DE,AD,BE之间的数量关系,并加以证明;
当直线MN绕点C旋转到图②的位置时,你在中得到的结论是否发生变化?请写出你的猜想,并加以证明;
当直线MN绕点C旋转到图③的位置时,你在中得到的结论是否发生变化?请写出你的猜想,并加以证明.
26.本小题8分
已知在五边形ABCDE中,,,连接AC,AD,且
如图①,若求证:;
如图②,在的条件下,连接BE,分别交AC,AD于M,N两点.若,AF为中边BE上的中线.求证:;
如图③,在的条件下,若,,则五边形ABCDE的面积为__________.
答案和解析
1.【答案】B
【解析】略
2.【答案】C
【解析】【分析】
此题考查了全等三角形的判定,掌握全等三角形的判定方法是关键,要使≌的条件必须满足SSS、SAS、ASA、AAS,可据此进行判断.
【解答】
解:第①组,,,满足AAS,能证明≌;
第②组,,满足SAS,能证明≌;
第③组,,满足ASA,能证明≌;
所以有3组能证明≌
故选
3.【答案】B
【解析】【分析】
本题考查了作图-基本作图、等腰三角形的性质,解决本题的关键是掌握等腰三角形的性质.根据等腰三角形的性质可得的度数,由邻补角关系求出度数,观察作图过程可得CE平分,利用角平分线定义而可得的度数.
【解答】
解:,,
,
,
观察作图过程可知:
CE平分,
,
的度数为,
故选:
4.【答案】C
【解析】略
5.【答案】B
【解析】略
6.【答案】C
【解析】略
7.【答案】B
【解析】略
8.【答案】D
【解析】延长BA至点E,使,连接则因为,所以又BD平分,所以在和中, 所以≌所以又,所以又,所以为等腰三角形.所以又,所以又,所以
9.【答案】B
【解析】【分析】
本题考查了全等三角形的判定与性质,三角形的外角性质,等腰三角形的判定与性质等内容.
在BC上截取,连接根据I是三条角平分线的交点,证得≌进而得,可得答案.
【解答】
解:在BC上截取,连接
因为,的平分线交于点I,
所以,
在和中,
所以≌
所以,
因为,,
所以,即
所以是等腰三角形
所以
所以
因为BI平分,所以
所以,即
所以
因为,
所以
10.【答案】A
【解析】在BA的延长线上取点E,使,连接因为AD是的外角平分线,所以在和中, 所以≌所以在中,又,所以,即因为,,,,所以
11.【答案】三角形的稳定性
【解析】略
12.【答案】答案不唯一,如:
【解析】略
13.【答案】
【解析】略
14.【答案】15
【解析】略
15.【答案】3
【解析】略
16.【答案】3
【解析】略
17.【答案】2或
【解析】因为四边形ABCD是长方形,,,所以,,所以与全等可分为≌或≌两种情况.当≌时,,所以所以又点P运动的速度为,所以点P运动的时间为此时,所以 ;当≌时,, .所以点P的运动时间为所以 .综上,当v的值为2或 时,与全等.
18.【答案】2
【解析】过点E作交OM于点所以所以又,所以又和都是等腰直角三角形,所以,,又,所以,即在和中, 所以≌所以,,即又,所以,即在和中, 所以≌所以又,所以
HB .又,所以,即
19.【答案】【小题1】
①
③
②
【小题2】
在和中, 所以≌所以
【解析】答案不唯一
略
20.【答案】【小题1】由题意,得,由折叠的性质,得,,,所以,又,所以≌
【小题2】
由,得,,所以, .又,,所以,即所以
【解析】见答案
见答案
21.【答案】【小题1】由题意,得在和中, 所以≌
【小题2】的大小无变化.理由如下:由,得≌,所以因为,,所以因为,所以因为,所以所以的大小无变化.
【解析】略
略
22.【答案】因为,所以因为,所以所以,即因为相邻两平行线间的距离相等,所以在和中, 所以≌所以又,所以则宣传墙CD的长度为
【解析】略
23.【答案】【小题1】因为,所以又,所以,即在和中, 所以≌
【小题2】
①如图,即为所作.
②平行
【解析】略
略
24.【答案】【小题1】
如图①:
【小题2】
能.如图②:
【小题3】
4
【解析】略
略
当已知角为两条边的夹角时,可画出1个满足条件的三角形;当3 cm长的边作为角的对边时,可画出2个满足条件的三角形;当4 cm长的边作为角的对边时,可画出1个满足条件的三角形.则符合条件的三角形共有个
25.【答案】【小题1】证明如下:因为,,所以因为,,所以所以所以在和中, 所以≌所以,所以
【小题2】发生变化,证明如下:因为,所以因为,,所以所以所以在和中, 所以≌所以,所以
【小题3】发生变化,证明如下:因为,所以因为,,所以所以所以在和中, 所以≌所以,所以
【解析】略
略
略
26.【答案】【小题1】
因为,所以又,所以又,,所以所以
【小题2】
延长AF,BC交于点G,设AG交CD于点P,如图.由,得≌,,,所以,又,所以,即所以所以又AF为中边BE上的中线,所以又,所以≌所以,即又,所以≌所以因为,所以,即所以又,所以所以
【小题3】
42
【解析】略
略
由,得,,,所以又,所以,即又,所以四边形ACDE是直角梯形.又,,,所以,所以 , .所以
第1页,共1页
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
