湖南省长沙市雅礼中学2025届高三上学期月考(二)数学试题(含答案)
文档属性
| 名称 | 湖南省长沙市雅礼中学2025届高三上学期月考(二)数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 251.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-20 15:28:49 | ||
图片预览




文档简介
湖南省长沙市雅礼中学2025届高三上学期月考(二)数学试题
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.若复数,则( )
A. B. C. D.
3.设,是单位向量,则的最小值是( )
A. B. C. D.
4.已知,则( )
A. B. C. D.
5.巴黎奥运会期间,旅客人数万人为随机变量,且记一天中旅客人数不少于万人的概率为,则的值约为( ) 参考数据:若,有,,
A. B. C. D.
6.已知抛物线:的焦点为,过点的直线与相交于,两点,则的最小值为( )
A. B. C. D.
7.若,,,则的取值范围为( )
A. B. C. D.
8.从重量分别为,,,,,克的砝码每种砝码各个中选出若干个,使其总重量恰为克的方法总数为,下列各式的展开式中的系数为的选项是( )
A.
B.
C.
D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列选项中,正确的是( )
A. 不等式的解集为或
B. 不等式的解集为
C. 不等式的解集为
D. 设,则“”是“”的充分不必要条件
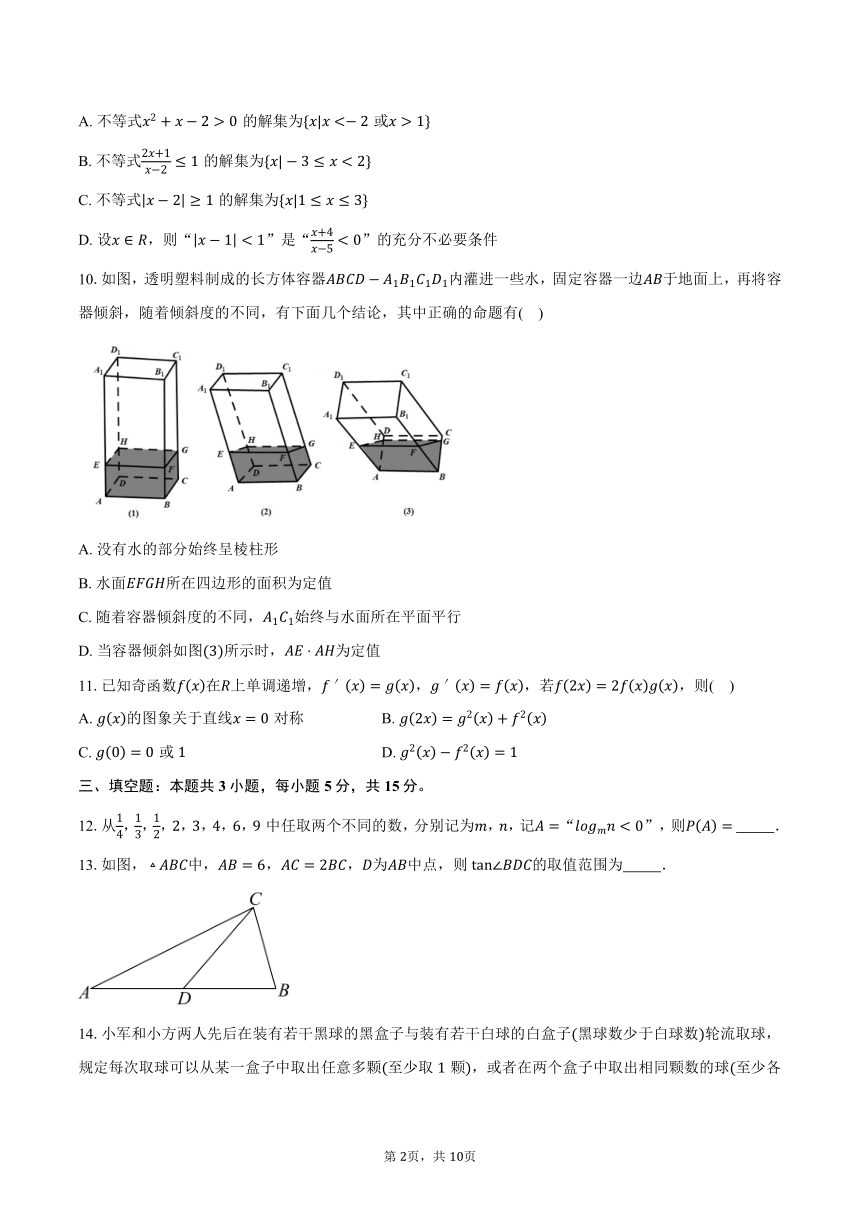
10.如图,透明塑料制成的长方体容器内灌进一些水,固定容器一边于地面上,再将容器倾斜,随着倾斜度的不同,有下面几个结论,其中正确的命题有( )
A. 没有水的部分始终呈棱柱形
B. 水面所在四边形的面积为定值
C. 随着容器倾斜度的不同,始终与水面所在平面平行
D. 当容器倾斜如图所示时,为定值
11.已知奇函数在上单调递增,,,若,则( )
A. 的图象关于直线对称 B.
C. 或 D.
三、填空题:本题共3小题,每小题5分,共15分。
12.从,,,,,,,中任取两个不同的数,分别记为,,记“”,则 .
13.如图,中,,,为中点,则的取值范围为 .
14.小军和小方两人先后在装有若干黑球的黑盒子与装有若干白球的白盒子黑球数少于白球数轮流取球,规定每次取球可以从某一盒子中取出任意多颗至少取颗,或者在两个盒子中取出相同颗数的球至少各取颗,最后不能按规则取的人输已知两盒中共有个球,且两人掷硬币后决定由小军先手取球小方看了眼黑盒中的球,对小军说:“你输了”若已知小方有必胜策略,则黑盒中球数为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
记的内角的对边分别为已知,.
求;
若的内切圆在上的切点为,求.
16.本小题分
已知动圆过点且与圆:内切.
求动圆圆心的轨迹的方程;
设动圆:,与相交于四点,动圆:与相交于四点若矩形与矩形的面积相等,求的值.
17.本小题分
为提高我国公民整体健康水平,年月,由国家卫生健康委疾控局指导、中国疾病预防控制中心和国家体育总局体育科学研究所牵头组织编制的中国人群身体活动指南以下简称指南正式发布,指南建议岁的成年人每周进行分钟中等强度或分钟高强度的有氧运动以下简称为“达标成年人”,经过两年的宣传,某体育健康机构为制作一期达标成年人的纪录片,采取街头采访的方式进行拍摄,当采访到第二位“达标成年人”时,停止当天采访记采访的岁的市民数为随机变量,且该市随机抽取的岁的市民是达标成年人的概率为,抽查结果相互独立.
求某天采访刚好到第五位可停止当天采访的概率;
若抽取的岁的市民数不超过的概率大于,求整数的最小值.
18.本小题分
已知函数.
当时,求的图象在点处的切线方程;
若时,,求的取值范围;
求证:.
19.本小题分
高斯博内公式是大范围微分几何学的一个经典的公式,是关于曲面的图形由曲率表征和拓扑由欧拉示性数表征间联系的一项重要表述,建立了空间的局部性质和整体性质之间的联系其特例是球面三角形总曲率与球面三角形内角和满足:,其中为常数,如图,把球面上的三个点用三个大圆以球心为半径的圆的圆弧联结起来,所围成的图形叫做球面三角形,每个大圆弧叫做球面三角形的一条边,两条边所在的半平面构成的二面角叫做球面三角形的一个角球面三角形的总曲率等于,为球面三角形面积,为球的半径.
若单位球面有一个球面三角形,三条边长均为,求此球面三角形内角和;
求的值;
把多面体的任何一个面伸展成平面,如果所有其他各面都在这个平面的同侧,这样的多面体叫做凸多面体设凸多面体顶点数为,棱数为,面数为,试证明凸多面体欧拉示性数为定值,并求出.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
由,则,
整理得:,
则角化边可得:,
整理可得:,
又,因此可得.
由知,
设的内切圆在上的切点为,
则,
则,
,
因此可得,即.
16.
设动圆半径为,则,内切,
,所以点的轨迹是以为焦点的椭圆.
,,.
则动圆圆心的轨迹的方程为:.
设,由矩形与矩形的面积相等,得
,故,
因为点,均在椭圆上,所以,,
整理可得:,
由,知,所以,同理可得,
因此.
17.
根据题意,某天采访刚好到第五位可停止当天采访,即采访的前四位中有一位是达标成年人,第五位必是达标成年人,
所以随机变量服从二项分布,
所以某天采访刚好到第五位可停止当天采访的概率为.
依题意,随机变量服从二项分布,则
所以,
化简得,
即,
记,
则,
由,可得,
即,解得,
由此可得,,即,
设,,
因为,可得数列是递减数列,
又,,
所以整数的最小值为.
18.
当时,,,
则,则,
所以在点处的切线方程为.
由时,,
即,整理得,对恒成立,
令,则,
令,,
所以,即函数在上单调递减,
所以,即,
所以函数在上单调递减,则,
.
设,,
则,
所以在上单调递减,则,即,
,,
令,,
可得,
所以,
,
,
,
以上式子相加得,
整理得,,
两边取指数得,,
即得,得证.
19.
如图,设球心为,球面三角形三个顶点分别为,
由球面三角形三边长均为,由题意,即每个大圆弧长均为.
又单位球面的球半径,则球面三角形每条边所对圆心角为,
所以在三棱锥中,两两垂直.
由,,且平面,平面,
则平面,平面,
故平面平面,同理平面平面,平面平面,
即球面三角形任意两条边所在的半平面构成的二面角均为,
故球面三角形的个角均为,从而此球面三角形内角和为.
若将地球看作一个球体,
在地球上零度经线和经线所在大圆与赤道所在大圆将球面平均分成个全等的球面三角形,
由可知,每个球面三角形的个角均为,且球面三角形内角和,
从而每个球面三角形的面积为,
则每个球面三角形的总曲率为,
设,由题意,且为 常数,
则有,从而.
将多面体的每个面视作可以自由伸缩的橡皮膜,使膨胀为一个半径为的球,
每个顶点均在球面上,每条边变为球面上的边,每个多边形变为球面上的多边形,
且膨胀前后不变.
不妨记球面仍为单位球面,半径,
对于任意一个球面边形,可用球面上的边分割成个球面三角形,
由可知,,则每个球面三角形的内角和.
即每个内角和为的球面三角形面积为,
记,称为分割成个球面三角形的球面边形的内角和.
所以球面边形面积为.
由已知凸多面体顶点数为,棱数为,面数为,
则可记球面上多边形,
对每一个球面多边形,设其边数为,内角和为,面积为,
则,
由球面三角形角的定义可知,每个顶点处所有球面多边形的角之和为,顶点数为,
从而所有球面多边形内角和为,
又球面多边形每条边被重复计算次,棱数为,故,
则,
又所有球面多边形面积之和,
故,故.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,,则( )
A. B. C. D.
2.若复数,则( )
A. B. C. D.
3.设,是单位向量,则的最小值是( )
A. B. C. D.
4.已知,则( )
A. B. C. D.
5.巴黎奥运会期间,旅客人数万人为随机变量,且记一天中旅客人数不少于万人的概率为,则的值约为( ) 参考数据:若,有,,
A. B. C. D.
6.已知抛物线:的焦点为,过点的直线与相交于,两点,则的最小值为( )
A. B. C. D.
7.若,,,则的取值范围为( )
A. B. C. D.
8.从重量分别为,,,,,克的砝码每种砝码各个中选出若干个,使其总重量恰为克的方法总数为,下列各式的展开式中的系数为的选项是( )
A.
B.
C.
D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列选项中,正确的是( )
A. 不等式的解集为或
B. 不等式的解集为
C. 不等式的解集为
D. 设,则“”是“”的充分不必要条件
10.如图,透明塑料制成的长方体容器内灌进一些水,固定容器一边于地面上,再将容器倾斜,随着倾斜度的不同,有下面几个结论,其中正确的命题有( )
A. 没有水的部分始终呈棱柱形
B. 水面所在四边形的面积为定值
C. 随着容器倾斜度的不同,始终与水面所在平面平行
D. 当容器倾斜如图所示时,为定值
11.已知奇函数在上单调递增,,,若,则( )
A. 的图象关于直线对称 B.
C. 或 D.
三、填空题:本题共3小题,每小题5分,共15分。
12.从,,,,,,,中任取两个不同的数,分别记为,,记“”,则 .
13.如图,中,,,为中点,则的取值范围为 .
14.小军和小方两人先后在装有若干黑球的黑盒子与装有若干白球的白盒子黑球数少于白球数轮流取球,规定每次取球可以从某一盒子中取出任意多颗至少取颗,或者在两个盒子中取出相同颗数的球至少各取颗,最后不能按规则取的人输已知两盒中共有个球,且两人掷硬币后决定由小军先手取球小方看了眼黑盒中的球,对小军说:“你输了”若已知小方有必胜策略,则黑盒中球数为 .
四、解答题:本题共5小题,共60分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
记的内角的对边分别为已知,.
求;
若的内切圆在上的切点为,求.
16.本小题分
已知动圆过点且与圆:内切.
求动圆圆心的轨迹的方程;
设动圆:,与相交于四点,动圆:与相交于四点若矩形与矩形的面积相等,求的值.
17.本小题分
为提高我国公民整体健康水平,年月,由国家卫生健康委疾控局指导、中国疾病预防控制中心和国家体育总局体育科学研究所牵头组织编制的中国人群身体活动指南以下简称指南正式发布,指南建议岁的成年人每周进行分钟中等强度或分钟高强度的有氧运动以下简称为“达标成年人”,经过两年的宣传,某体育健康机构为制作一期达标成年人的纪录片,采取街头采访的方式进行拍摄,当采访到第二位“达标成年人”时,停止当天采访记采访的岁的市民数为随机变量,且该市随机抽取的岁的市民是达标成年人的概率为,抽查结果相互独立.
求某天采访刚好到第五位可停止当天采访的概率;
若抽取的岁的市民数不超过的概率大于,求整数的最小值.
18.本小题分
已知函数.
当时,求的图象在点处的切线方程;
若时,,求的取值范围;
求证:.
19.本小题分
高斯博内公式是大范围微分几何学的一个经典的公式,是关于曲面的图形由曲率表征和拓扑由欧拉示性数表征间联系的一项重要表述,建立了空间的局部性质和整体性质之间的联系其特例是球面三角形总曲率与球面三角形内角和满足:,其中为常数,如图,把球面上的三个点用三个大圆以球心为半径的圆的圆弧联结起来,所围成的图形叫做球面三角形,每个大圆弧叫做球面三角形的一条边,两条边所在的半平面构成的二面角叫做球面三角形的一个角球面三角形的总曲率等于,为球面三角形面积,为球的半径.
若单位球面有一个球面三角形,三条边长均为,求此球面三角形内角和;
求的值;
把多面体的任何一个面伸展成平面,如果所有其他各面都在这个平面的同侧,这样的多面体叫做凸多面体设凸多面体顶点数为,棱数为,面数为,试证明凸多面体欧拉示性数为定值,并求出.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
由,则,
整理得:,
则角化边可得:,
整理可得:,
又,因此可得.
由知,
设的内切圆在上的切点为,
则,
则,
,
因此可得,即.
16.
设动圆半径为,则,内切,
,所以点的轨迹是以为焦点的椭圆.
,,.
则动圆圆心的轨迹的方程为:.
设,由矩形与矩形的面积相等,得
,故,
因为点,均在椭圆上,所以,,
整理可得:,
由,知,所以,同理可得,
因此.
17.
根据题意,某天采访刚好到第五位可停止当天采访,即采访的前四位中有一位是达标成年人,第五位必是达标成年人,
所以随机变量服从二项分布,
所以某天采访刚好到第五位可停止当天采访的概率为.
依题意,随机变量服从二项分布,则
所以,
化简得,
即,
记,
则,
由,可得,
即,解得,
由此可得,,即,
设,,
因为,可得数列是递减数列,
又,,
所以整数的最小值为.
18.
当时,,,
则,则,
所以在点处的切线方程为.
由时,,
即,整理得,对恒成立,
令,则,
令,,
所以,即函数在上单调递减,
所以,即,
所以函数在上单调递减,则,
.
设,,
则,
所以在上单调递减,则,即,
,,
令,,
可得,
所以,
,
,
,
以上式子相加得,
整理得,,
两边取指数得,,
即得,得证.
19.
如图,设球心为,球面三角形三个顶点分别为,
由球面三角形三边长均为,由题意,即每个大圆弧长均为.
又单位球面的球半径,则球面三角形每条边所对圆心角为,
所以在三棱锥中,两两垂直.
由,,且平面,平面,
则平面,平面,
故平面平面,同理平面平面,平面平面,
即球面三角形任意两条边所在的半平面构成的二面角均为,
故球面三角形的个角均为,从而此球面三角形内角和为.
若将地球看作一个球体,
在地球上零度经线和经线所在大圆与赤道所在大圆将球面平均分成个全等的球面三角形,
由可知,每个球面三角形的个角均为,且球面三角形内角和,
从而每个球面三角形的面积为,
则每个球面三角形的总曲率为,
设,由题意,且为 常数,
则有,从而.
将多面体的每个面视作可以自由伸缩的橡皮膜,使膨胀为一个半径为的球,
每个顶点均在球面上,每条边变为球面上的边,每个多边形变为球面上的多边形,
且膨胀前后不变.
不妨记球面仍为单位球面,半径,
对于任意一个球面边形,可用球面上的边分割成个球面三角形,
由可知,,则每个球面三角形的内角和.
即每个内角和为的球面三角形面积为,
记,称为分割成个球面三角形的球面边形的内角和.
所以球面边形面积为.
由已知凸多面体顶点数为,棱数为,面数为,
则可记球面上多边形,
对每一个球面多边形,设其边数为,内角和为,面积为,
则,
由球面三角形角的定义可知,每个顶点处所有球面多边形的角之和为,顶点数为,
从而所有球面多边形内角和为,
又球面多边形每条边被重复计算次,棱数为,故,
则,
又所有球面多边形面积之和,
故,故.
第1页,共1页
同课章节目录
