2024-2025学年北师大版八年级上册数学期中测试题(1-3单元)(含答案)
文档属性
| 名称 | 2024-2025学年北师大版八年级上册数学期中测试题(1-3单元)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 328.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-21 00:00:00 | ||
图片预览



文档简介
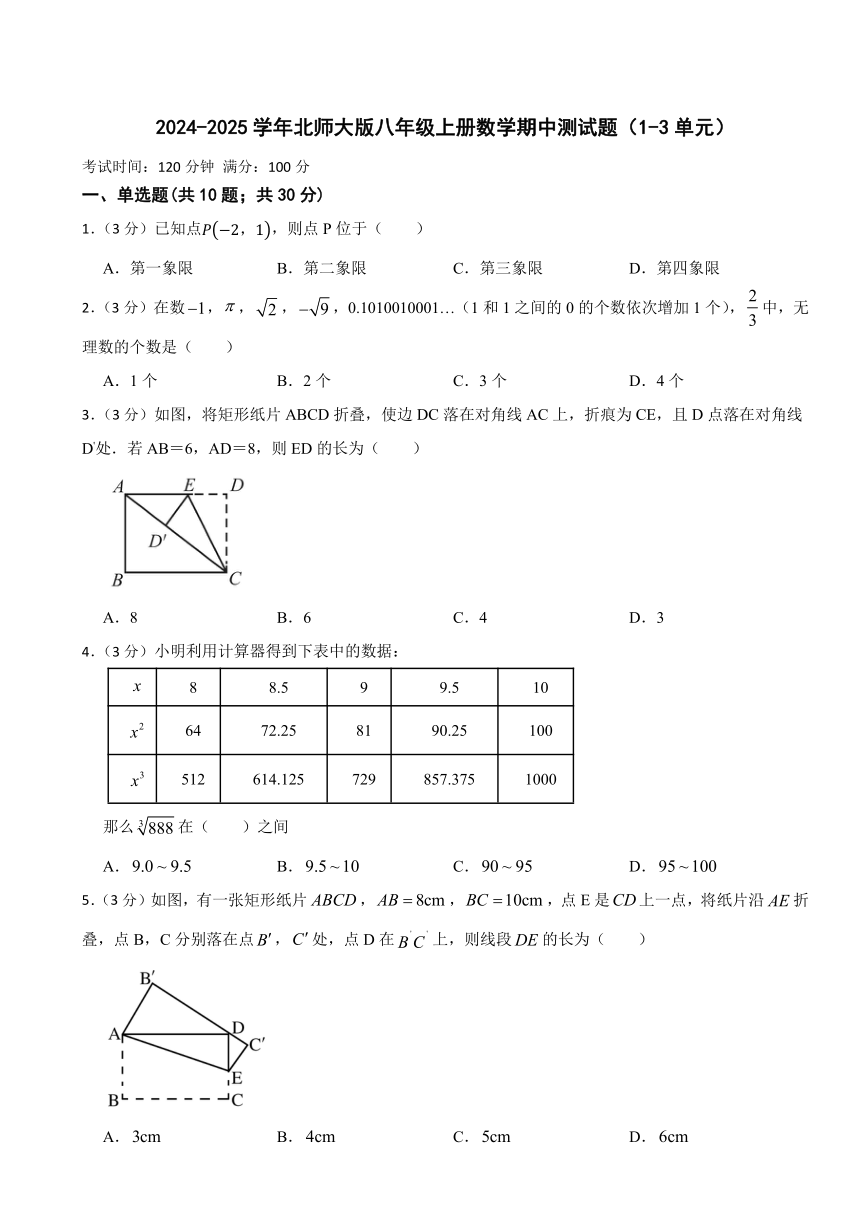
2024-2025学年北师大版八年级上册数学期中测试题(1-3单元)
考试时间:120分钟 满分:100分
一、单选题(共10题;共30分)
1.(3分)已知点,则点P位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(3分)在数,,,,0.1010010001…(1和1之间的0的个数依次增加1个),中,无理数的个数是( )
A.1个 B.2个 C.3个 D.4个
3.(3分)如图,将矩形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D'处.若AB=6,AD=8,则ED的长为( )
A.8 B.6 C.4 D.3
4.(3分)小明利用计算器得到下表中的数据:
8 8.5 9 9.5 10
64 72.25 81 90.25 100
512 614.125 729 857.375 1000
那么在( )之间
A. B. C. D.
5.(3分)如图,有一张矩形纸片,,,点E是上一点,将纸片沿折叠,点B,C分别落在点,处,点D在上,则线段的长为( )
A. B. C. D.
6.(3分)如图,正方形的对角线交于点O,点E是直线上一动点.若,则的最小值是( )
A. B. C. D.
7.(3分)数学课上,老师让同学们以“矩形的折叠”为主题开展数学活动.如图,小明把矩形沿折叠,使点落在边的点处,其中,且,则矩形的面积为( )
A. B. C. D.
8.(3分)设681×2019﹣681×2018=a,2015×2016﹣2013×2018=b, ,则a,b,c的大小关系是( )
A.b<c<a B.a<c<b C.b<a<c D.c<b<a
9.(3分)如图,中,,,.以,为直角边,构造;再以,为直角边,构造;……,按照这个规律,在中,点到的距离是( )
A. B. C. D.
10.(3分)在数轴上有三个互不重合的点A,B,C,它们代表的实数分别为a,b,c,下列结论中①若abc 0,则A,B,C三点中,至少有一个点在原点右侧;②若a+b+c=0,则A,B,C三点中,至少有一个点在原点右侧;③若a+c=2b,则点B为线段AC的中点;④O为坐标原点且A,B,C均不与O重合,若OB﹣OC=AB﹣AC,则bc 0,
所有正确结论的序号是( )
A.①② B.③④ C.①②③ D.①②③④
二、填空题(共7题;共24分)
11.(3分)如图,矩形ABCD的面积为60,一条边AB的长为5,则矩形的对角线BD= .
12.(3分)若点P的坐标是(﹣4,2),则点P关于原点的对称点坐标是 .
13.(3分)如图,在中,,,,点,分别在,上,将沿直线翻折,点的对应点恰好落在上,连接,若,则的长为 .
14.(6分)在平面直角坐标系中,点P(-3,2)在第 象限;点P到x轴的距离是 .
15.(3分)如图,长方形ABCD的各边分别平行于x轴或y轴,A,B,C,D的坐标分别为(﹣2,1)(2,1)(2,﹣1)(﹣2,﹣1)物体甲和物体乙分别由E(﹣2,0)和F(2,0)同时出发,沿长方形的边按逆时针方向同向行进,甲的速度每秒4个单位长度,乙的速度每秒1个单位长度,则两个物体第2019次相遇地点的坐标为 .
16.(3分)如图,在矩形 中, .分别以点 为圆心,以大于 的长为半径画弧,两弧相交于点 和 .作直线 分别与 交于点 ,则 .
17.(3分)如图,长方形ABOC中点A坐标为(4,5),点E是x轴上一动点,连接AE,把∠B沿AE折叠,当点B落在y轴上时点E的坐标为 .
三、解答题(共7题;共46分)
18.(6分)计算:
(1)(3分)
(2)(3分)
19.(6分)如图,正方形ABCD的面积为8,正方形ECFG的面积为32.
(1)(3分)求正方形ABCD和正方形ECFG的边长;
(2)(3分)求阴影部分的面积.
20.(6分)如图,小明将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端6m处,发现此时绳子底端距离打结处约2m.请设法算出旗杆的高度.
21.(6分)(1)如图1,在四边形中,,,,,,求四边形的面积.
(2)如图2,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子的长为13米,此人以米每秒的速度收绳,6秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)
22.(7分)求出下列各数的相反数,在数轴上表示下列各数以及它们的相反数,并用“<”连接:
.
23.(7分)我国古代数学著作《九章算术》中有一个问题,原文是:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何.(丈、尺是长度单位,1丈=10尺).意思是有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水的深度与这根芦苇的长度分别是多少?
24.(8分)如图,已知数轴上点A表示的数为-10,B是数轴上在A右侧的一点,且A,B两点间的距离为16.动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
(1)(2分)数轴上点B表示的数是 ,点P表示的数是 (用含t的代数式表示);
(2)(3分)在点P开始运动后第几秒时,P到A、B两点的距离之和为20,请说明理由;
(3)(3分)若动点Q同时从点B出发,以每秒1个单位长度的速度沿数轴向右匀速运动,试判断:2AQ-AP的值是否会随着t的变化而变化?请说明理由.
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】D
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】A
8.【答案】A
9.【答案】B
10.【答案】D
11.【答案】13
12.【答案】(4,﹣2)
13.【答案】7.5
14.【答案】二;2
15.【答案】(1,﹣1)
16.【答案】2
17.【答案】( ,0)或(﹣6,0)
18.【答案】(1)解:
(2)解:
19.【答案】(1)正方形ABCD的边长为2,正方形ECFG的边长为4
(2)阴影部分的面积为12
20.【答案】旗杆高8米
21.【答案】(1)36;(2)船向岸边移动了米
22.【答案】解: 的相反数为 ,
的相反数为 ,
0的相反数为0,
因为 ,
所以 的相反数为2;
将各数以及它们的相反数在数轴上表示出来如下图:
用“<”连接:
.
23.【答案】解:设水深尺,芦苇尺,1丈=10尺,
由勾股定理:,
解得:,
∴,
答:水深12尺,芦苇的长度是13尺.
24.【答案】(1)6;-10+2t
(2)在点P开始运动后第9秒时,P到A、B两点的距离之和为20.理由如下:
根据题意可知,当P到A、B两点的距离之和为20时,点P应位于点B的右侧.
∵PA+PB=AB+2PB=20,
∴2PB=20-AB=20-16=4,
∴PB=2,
∴点P表示的数为6+2=8,
∴-10+2t=8,
解得t=9.
∴在点P开始运动后第9秒时,P到A、B两点的距离之和为20.
(3)解:2AQ-AP的值不会随着t的变化而变化.理由如下:
根据题意,点Q表示的数为6+t.
∵AQ=6+t-(-10)=16+t,AP=2t,
∴2AQ-AP=2(16+t)-2t=32,
∴2AQ-AP的值不会随着t的变化而变化.
考试时间:120分钟 满分:100分
一、单选题(共10题;共30分)
1.(3分)已知点,则点P位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(3分)在数,,,,0.1010010001…(1和1之间的0的个数依次增加1个),中,无理数的个数是( )
A.1个 B.2个 C.3个 D.4个
3.(3分)如图,将矩形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D'处.若AB=6,AD=8,则ED的长为( )
A.8 B.6 C.4 D.3
4.(3分)小明利用计算器得到下表中的数据:
8 8.5 9 9.5 10
64 72.25 81 90.25 100
512 614.125 729 857.375 1000
那么在( )之间
A. B. C. D.
5.(3分)如图,有一张矩形纸片,,,点E是上一点,将纸片沿折叠,点B,C分别落在点,处,点D在上,则线段的长为( )
A. B. C. D.
6.(3分)如图,正方形的对角线交于点O,点E是直线上一动点.若,则的最小值是( )
A. B. C. D.
7.(3分)数学课上,老师让同学们以“矩形的折叠”为主题开展数学活动.如图,小明把矩形沿折叠,使点落在边的点处,其中,且,则矩形的面积为( )
A. B. C. D.
8.(3分)设681×2019﹣681×2018=a,2015×2016﹣2013×2018=b, ,则a,b,c的大小关系是( )
A.b<c<a B.a<c<b C.b<a<c D.c<b<a
9.(3分)如图,中,,,.以,为直角边,构造;再以,为直角边,构造;……,按照这个规律,在中,点到的距离是( )
A. B. C. D.
10.(3分)在数轴上有三个互不重合的点A,B,C,它们代表的实数分别为a,b,c,下列结论中①若abc 0,则A,B,C三点中,至少有一个点在原点右侧;②若a+b+c=0,则A,B,C三点中,至少有一个点在原点右侧;③若a+c=2b,则点B为线段AC的中点;④O为坐标原点且A,B,C均不与O重合,若OB﹣OC=AB﹣AC,则bc 0,
所有正确结论的序号是( )
A.①② B.③④ C.①②③ D.①②③④
二、填空题(共7题;共24分)
11.(3分)如图,矩形ABCD的面积为60,一条边AB的长为5,则矩形的对角线BD= .
12.(3分)若点P的坐标是(﹣4,2),则点P关于原点的对称点坐标是 .
13.(3分)如图,在中,,,,点,分别在,上,将沿直线翻折,点的对应点恰好落在上,连接,若,则的长为 .
14.(6分)在平面直角坐标系中,点P(-3,2)在第 象限;点P到x轴的距离是 .
15.(3分)如图,长方形ABCD的各边分别平行于x轴或y轴,A,B,C,D的坐标分别为(﹣2,1)(2,1)(2,﹣1)(﹣2,﹣1)物体甲和物体乙分别由E(﹣2,0)和F(2,0)同时出发,沿长方形的边按逆时针方向同向行进,甲的速度每秒4个单位长度,乙的速度每秒1个单位长度,则两个物体第2019次相遇地点的坐标为 .
16.(3分)如图,在矩形 中, .分别以点 为圆心,以大于 的长为半径画弧,两弧相交于点 和 .作直线 分别与 交于点 ,则 .
17.(3分)如图,长方形ABOC中点A坐标为(4,5),点E是x轴上一动点,连接AE,把∠B沿AE折叠,当点B落在y轴上时点E的坐标为 .
三、解答题(共7题;共46分)
18.(6分)计算:
(1)(3分)
(2)(3分)
19.(6分)如图,正方形ABCD的面积为8,正方形ECFG的面积为32.
(1)(3分)求正方形ABCD和正方形ECFG的边长;
(2)(3分)求阴影部分的面积.
20.(6分)如图,小明将升旗的绳子拉到旗杆底端,并在绳子上打了一个结,然后将绳子拉到离旗杆底端6m处,发现此时绳子底端距离打结处约2m.请设法算出旗杆的高度.
21.(6分)(1)如图1,在四边形中,,,,,,求四边形的面积.
(2)如图2,在离水面高度为5米的岸上,有人用绳子拉船靠岸,开始时绳子的长为13米,此人以米每秒的速度收绳,6秒后船移动到点D的位置,问船向岸边移动了多少米?(假设绳子是直的,结果保留根号)
22.(7分)求出下列各数的相反数,在数轴上表示下列各数以及它们的相反数,并用“<”连接:
.
23.(7分)我国古代数学著作《九章算术》中有一个问题,原文是:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问水深、葭长各几何.(丈、尺是长度单位,1丈=10尺).意思是有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.水的深度与这根芦苇的长度分别是多少?
24.(8分)如图,已知数轴上点A表示的数为-10,B是数轴上在A右侧的一点,且A,B两点间的距离为16.动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
(1)(2分)数轴上点B表示的数是 ,点P表示的数是 (用含t的代数式表示);
(2)(3分)在点P开始运动后第几秒时,P到A、B两点的距离之和为20,请说明理由;
(3)(3分)若动点Q同时从点B出发,以每秒1个单位长度的速度沿数轴向右匀速运动,试判断:2AQ-AP的值是否会随着t的变化而变化?请说明理由.
答案解析部分
1.【答案】B
2.【答案】C
3.【答案】D
4.【答案】B
5.【答案】C
6.【答案】D
7.【答案】A
8.【答案】A
9.【答案】B
10.【答案】D
11.【答案】13
12.【答案】(4,﹣2)
13.【答案】7.5
14.【答案】二;2
15.【答案】(1,﹣1)
16.【答案】2
17.【答案】( ,0)或(﹣6,0)
18.【答案】(1)解:
(2)解:
19.【答案】(1)正方形ABCD的边长为2,正方形ECFG的边长为4
(2)阴影部分的面积为12
20.【答案】旗杆高8米
21.【答案】(1)36;(2)船向岸边移动了米
22.【答案】解: 的相反数为 ,
的相反数为 ,
0的相反数为0,
因为 ,
所以 的相反数为2;
将各数以及它们的相反数在数轴上表示出来如下图:
用“<”连接:
.
23.【答案】解:设水深尺,芦苇尺,1丈=10尺,
由勾股定理:,
解得:,
∴,
答:水深12尺,芦苇的长度是13尺.
24.【答案】(1)6;-10+2t
(2)在点P开始运动后第9秒时,P到A、B两点的距离之和为20.理由如下:
根据题意可知,当P到A、B两点的距离之和为20时,点P应位于点B的右侧.
∵PA+PB=AB+2PB=20,
∴2PB=20-AB=20-16=4,
∴PB=2,
∴点P表示的数为6+2=8,
∴-10+2t=8,
解得t=9.
∴在点P开始运动后第9秒时,P到A、B两点的距离之和为20.
(3)解:2AQ-AP的值不会随着t的变化而变化.理由如下:
根据题意,点Q表示的数为6+t.
∵AQ=6+t-(-10)=16+t,AP=2t,
∴2AQ-AP=2(16+t)-2t=32,
∴2AQ-AP的值不会随着t的变化而变化.
同课章节目录
