2024-2025北师大版八年级数学上册 第三章 位置与坐标 题型总结试卷(无答案)
文档属性
| 名称 | 2024-2025北师大版八年级数学上册 第三章 位置与坐标 题型总结试卷(无答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-21 16:01:30 | ||
图片预览


文档简介
北师大版八年级数学(上)第三章位置与坐标题型总结
题组一 平面直角坐标系坐标特征
1.下列各点中在第四象限的是( )
A.(﹣3,7) B.(3,﹣7) C.(3,7) D.(﹣3,﹣7)
2.在平面直角坐标系中,若点P(m,m﹣n)与点Q(2,1)关于原点对称,则点M(m,n)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.平面直角坐标系中,点A在第四象限,点A到x轴的距离为2,到y轴的距离为3,则点A的坐标为( )
A.(2,﹣3) B.(﹣3,2) C.(3,﹣2) D.(﹣2,3)
4.下列说法正确的是( )
A.点(1,﹣a2)在第四象限 B.若ab=0,则P(a,b)在坐标原点
C.点P在第二象限,且点P到x轴的距离为2,点P到y轴的距离为3,则点P的坐标为(﹣3,2)
D.在平面直角坐标系中,若点A的坐标为(﹣1,﹣2),且AB平行于x轴,AB=5,则点B的坐标为(4,﹣2)
5.下列说法不正确的是( )
A.在x轴上的点的纵坐标为0 B.点P(﹣1,3)到y轴的距离是1
C.若xy<0,x﹣y>0,那么点Q(x,y)在第四象限 D.点A(﹣a2﹣1,|b|)一定在第二象限
题组二 基本对称变换
6.在平面直角坐标系中,坐标为(a,b)的点关于x轴对称的点的坐标为( )
A.(a,﹣b) B.(b,a) C.(﹣a,b) D.(﹣b,﹣a)
7.点A(1,﹣2)经过某种图形变化后得到点A′(2,1),这种图形变化可以是( )
A.绕原点逆时针旋转90° B.绕原点顺时针旋转90° C.关于x轴对称 D.关于y轴对称
8.点A(2023,﹣2024)关于y轴对称的点的坐标为( )
A.(﹣2024,2023) B.(2023,﹣2024) C.(﹣2023,﹣2024) D.(2023,2024)
9.在直角坐标系中,已知点A(2+a,b﹣2),B(b,1)关于原点对称,则a,b的值是( )
A.a=0,b=0 B.a=﹣3,b=1 C.a=1,b=﹣3 D.a=5,b=3
10.若点A(a+b,﹣1)与点B(5,a﹣b) 关于原点对称,则点P(a,b)的坐标是( )
A.(2,3) B.(3,2) C.(﹣2,﹣3) D.(﹣3,﹣2)
题组三 关于x=a对称
11.平面直角坐标系中,已知点P(a,﹣3)在第四象限,则点P关于直线x=2对称的点的坐标是( )
A.(a,1) B.(﹣a+2,﹣3) C.(﹣a+4,﹣3) D.(﹣a,﹣3)
12.在平面直角坐标系中,点P(﹣2,3)关于直线x=1的对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
13.在平面直角坐标系中,已知A(4,3),A′与A关于直线x=1轴对称,则A′的坐标为( )
A.(﹣4,3) B.(4,﹣1) C.(﹣2,3) D.(4,﹣3)
14.平面直角坐标系中,已知点P(a,3)在第二象限,则点P关于直线m(直线m上各点的横坐标都是2)对称的点的坐标是( )
A.(﹣a,3) B.(a,﹣3) C.(﹣a+2,3) D.(﹣a+4,3)
15.在平面直角坐标系中,已知点P(a2+2,5),则点P关于直线m(直线m上各点的横坐标都为﹣2)对称点的坐标是( )
A.(﹣a2+6,5) B.(﹣a2﹣6,5) C.(a2﹣6,5) D.(﹣a2+4,5)
题组四 关于y=b对称
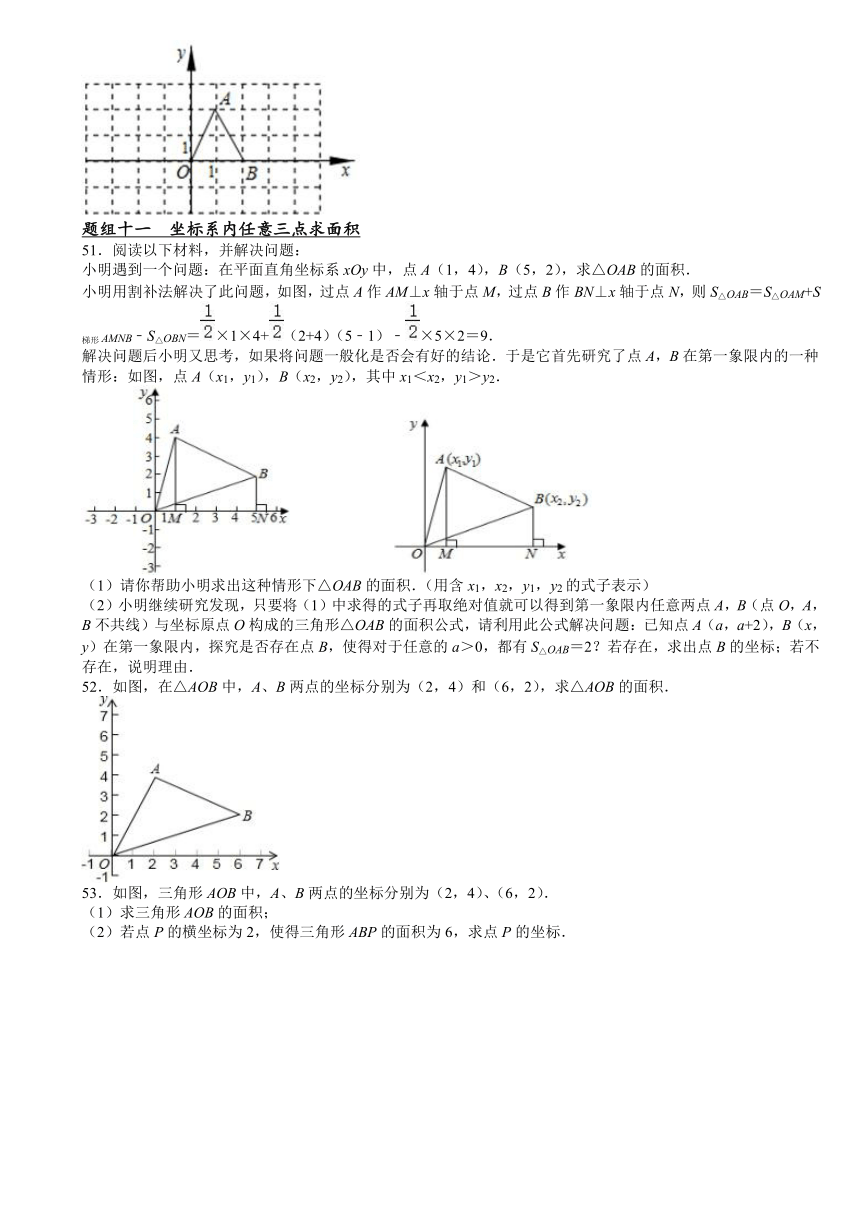
16.已知A(﹣4,1),那么A点关于直线y=﹣1对称的点的坐标为( )
A.(4,1) B.(﹣4,﹣1) C.(﹣4,﹣3) D.(﹣4,3)
17.如图点A和B关于直线y=1对称,已知点A坐标是(4,4),则点B的坐标是( )
18题图
A.(4,﹣4) B.(4,﹣2) C.(﹣2,4) D.(﹣4,2)
18.点P(﹣2,1)与点Q(a,b)关于直线y=﹣1对称,则点Q的坐标为( )
A.(﹣2,﹣3) B.(﹣2,﹣1) C.(﹣2,﹣2) D.(﹣2,﹣4)
19.在直角坐标系中,点A与点C关于直线y=2成轴对称,已知点A的坐标是(5,5),则点C的坐标是( )
A.(5,﹣5) B.(5,﹣1) C.(﹣2,5) D.(﹣5,1)
20.若点P(﹣2,a),Q(b,3),且PQ∥x轴,则a,b的值为( )
A.a=3,b≠2 B.a=3,b≠﹣2 C.a≠﹣3,b=2 D.a≠﹣3,b=﹣2
题组五 一三象限角平分线上的点
21.在平面直角坐标系中,点P(2m+3,3m﹣1)在第一三象限角平分线上,则点P的坐标为( )
A.(4,4) B.(3,3) C.(11,11) D.(﹣11,﹣11)
22.已知点P(5﹣a,2a﹣1)在一、三象限的角平分线上,则a的值为( )
A.﹣1 B.0 C.1 D.2
23.已知点P(a,2a+1)在一、三象限的角平分线上,则a的值为( )
A.﹣1 B.0 C.1 D.2
24.已知点P(a,1)在一、三象限的角平分线上,则a的值为( )
A.﹣1 B.0 C.1 D.2
25.已知点P(a,2a﹣1)在一、三象限的角平分线上,则a的值为( )
A.﹣1 B.0 C.1 D.2
题组六 二四象限角平分线上的点
26.已知点A(2a+1,5a﹣2)在第一、三象限的角平分线上,点B(2m+7,m﹣1)在二、四象限的角平分线上,则( )
A.a=1,m=﹣2 B.a=1,m=2 C.a=﹣1,m=﹣2 D.a=﹣1,m=2
27.已知点P(a,b)在第一、三或二、四象限坐标轴夹角的角平分线上,则有( )
A.a+b=0 B.a﹣b=0 C.a2﹣b2=0 D.a2+b2=0
28.点P(3﹣2x,5﹣x)在二、四象限的角平分线上,则x=( )
A. B.2 C. D.﹣2
29.点P(2x,y)在二、四象限的角平分线上,则( )
A.2x=y B.2x=﹣y C.﹣x=y D.|﹣2x|=y
30.若x+y=0,则点P(x,y)的位置是( )
A.一、三象限的角平分线上 B.二、四象限的角平分线上
C.二、三象限的角平分线上 D.一、四象限的角平分线上
题组七 关于一三象限角平分线对称
31.如图,在平面直角坐标系中,线段OA与OA′关于一、三象限的角平分线对称,已知点A的坐标为(2,1),则点A′的坐标为 .
32题图34题图
32.(1)如图,点P(﹣2,1)与点Q(a,b)关于直线l(y=﹣1)对称,则a+b= ;
(2)在平面直角坐标系中,点P(﹣3,2)关于第一、三象限角平分线对称的点的坐标是 .
33.点M(﹣1,3)关于第一、三象限的角平分线对称的点的坐标为 .
34.如图,第一、三象限角平分线记为y=x,如点(﹣1,﹣2)关于直线y=x对称点坐标为(﹣2,﹣1),点(a,b)关于y=x对称点的坐标为 .
35.点A(a,b)关于第一、三象限的角平分线(y=x)的对称点的坐标为A4 .
题组八 关于二四象限角平分线对称
36.已知点A(﹣2,3).若A、B两点关于x轴对称,则B的坐标为 ;若A、B两点关于二、四象限角平分线对称,则B的坐标为 .
37.已知点A(m,﹣3),B(2,n).若点A、B关于y轴对称,则m= ,n= ;若A、B在二、四象限的角平分线上,则m= ,n= .
38.点P(a,b)关于二四象限的角平分线的对称点表示为 .
39.点P(2,1)关于y=﹣x对称的点的坐标是 .
40.在平面直角坐标系中,点P(﹣4,﹣2)关于直线y=﹣x对称的点P′的坐标为 .
题组九 点的平移变换
41.在平面直角坐标系中,线段AB两个端点A(1,2),B(7,5).将线段AB平移后,点A的新坐标为(﹣6,﹣3),则点B的新坐标为 .
42.直角坐标系中,已知线段AB的两个端点分别是A(3,﹣2),B(1,1),将线段AB平移后得到线段A1B1.若点A1的坐标为(﹣1,2),则点B1的坐标为 .
43.在平面直角坐标系中,已知线段AB的两个端点分别是A(1,2),B(2,0),将线段AB平移后得到线段CD,其中,点A的对应点为点C,若C(3,a),D(b,1),则a﹣b的值为 .
44.线段AB的两个端点的坐标为A(m,2),B(3,5),将线段AB平移后得线段A′B′,其中A′(0,3),B′(6,n),则线段AB上的点C(﹣1,3)平移后的坐标是 .
45.如图,在平面直角坐标系中,点A,B的坐标分别为(﹣2,0)和(0,1),将线段AB平移,若平移后A,B的对应点为C(﹣1,m),D(n,3),则m+n的值是
题组十 点的规律变换
46.如图,在平面直角坐标系中,将等边△OAB绕点A旋转180°得到△O1AB,再将ΔO1AB1绕点O1旋转180°得到△O1A1B2,再将△O1A1B2绕点A1旋转180°得到△O2A1B,…,按此规律进行下去,若点B的坐标为(﹣2,0),则点B2024的坐标为 .
47题图 48题图
47.如图所示,长方形ABCD的两边BC、CD分别在x轴、y轴上,点C与原点重合,点A的坐标为(2,3),将长方形ABCD沿x轴无滑动向右翻滚,经过一次翻滚,点A的对应点记为A1;经过第二次翻滚,点A的对应点记为A2;……依次类推,经过第2024次翻滚,点A的对应点A2024的坐标为 .
48.如图,在平面直角坐标系xOy中,已知抛物线y=﹣x(x﹣3)(0≤x≤3)在x轴上方的部分,记作C1,它与x轴交于点O,A1,将C1绕点A1旋转180°得C2,C2与x轴交于另一点A2.请继续操作并探究:将C2绕点A2旋转180°得C3,与x轴交于另一点A3;将C3绕点A2旋转180°得C4,与x轴交于另一点A4,这样依次得到x轴上的点A1,A2,A3,…,An,…,及抛物线C1,C2,…, n,….则点A4的坐标为 ; n的顶点坐标为 (n为正整数,用含n的代数式表示).
49.已知:如图,直线l:y=﹣x﹣1,一组可由平移变换得到的抛物线的顶点为B1,B2、B3、…Bn(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0)(n为正整数),其中x1=0,x2=2,则x3= ;B8的坐标为 .
50.在平面直角坐标系中,△OAB的位置如图所示,将△OAB绕点O顺时针旋转90°得△OA1B1;再将△OA1B1绕点O顺时针旋转90°得△OA2B2;再将△OA2B2绕点O顺时针旋转90°得△OA3B3;……依此类推,第2021次旋转得到△OA2021B2021,则顶点A的对应点A2021的坐标是 .
题组十一 坐标系内任意三点求面积
51.阅读以下材料,并解决问题:
小明遇到一个问题:在平面直角坐标系xOy中,点A(1,4),B(5,2),求△OAB的面积.
小明用割补法解决了此问题,如图,过点A作AM⊥x轴于点M,过点B作BN⊥x轴于点N,则S△OAB=S△OAM+S梯形AMNB﹣S△OBN=×1×4+(2+4)(5﹣1)﹣×5×2=9.
解决问题后小明又思考,如果将问题一般化是否会有好的结论.于是它首先研究了点A,B在第一象限内的一种情形:如图,点A(x1,y1),B(x2,y2),其中x1<x2,y1>y2.
(1)请你帮助小明求出这种情形下△OAB的面积.(用含x1,x2,y1,y2的式子表示)
(2)小明继续研究发现,只要将(1)中求得的式子再取绝对值就可以得到第一象限内任意两点A,B(点O,A,B不共线)与坐标原点O构成的三角形△OAB的面积公式,请利用此公式解决问题:已知点A(a,a+2),B(x,y)在第一象限内,探究是否存在点B,使得对于任意的a>0,都有S△OAB=2?若存在,求出点B的坐标;若不存在,说明理由.
52.如图,在△AOB中,A、B两点的坐标分别为(2,4)和(6,2),求△AOB的面积.
53.如图,三角形AOB中,A、B两点的坐标分别为(2,4)、(6,2).
(1)求三角形AOB的面积;
(2)若点P的横坐标为2,使得三角形ABP的面积为6,求点P的坐标.
54.△ABC的顶点坐标分别是A(﹣1,2),B(﹣3,0),C(2,0),求△ABC的面积.
55.如图,已知:A(2,0),B(0,﹣2),点P(a,1),S△PAB>5,求a的取值范围.
题组十二 作图--对称变换
56.在正方形网格中,每个小正方形的边长为1,点A(﹣4,5),C(﹣1,3),A1(4,5),B1(2,1),△ABC与△A1B1C1关于某直线成轴对称.
(1)在网格内完善平面直角坐标系;
(2)点B坐标是 ,点C1坐标是 ;
(3)求△A1B1C1的面积.
57.如图,在平面直角坐标系中,每个小正方形的边长均为1,请回答下列问题:
(1)点A在第 象限,它的坐标是 ;
(2)点B在第 象限,它的坐标是 ;
(3)将△AOB的每个顶点的横坐标保持不变,纵坐标都乘以﹣1,再顺次连接这些点,所得的图形与△AOB关于 轴对称.
58.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(2,﹣1),B(1,﹣2),C(3,﹣3).
(1)请画出与△ABC关于y轴对称的△A1B1C1,并写出点C1的坐标;
(2)在(1)的条件下,画出与△A1B1C1关于直线l对称的△A2B2C2;
(3)在(2)的条件下,若点P1(m,n)在△A1B1C1的内部,则点P1在△A2B2C2中对应点P2的坐标是 .
59.如图,在平面直角坐标系中,已知点A(﹣4,1);B(1,1),C(﹣3,3).
(1)判断△ABC的形状,并说明理由;
(2)若点C关于直线AB的对称点为点D,则点D的坐标为 ;
(3)连接CD,BD,则△BCD的周长为 .
60.如图已知平面直角坐标系中A(﹣1,3),B(2,0),C(﹣3,﹣1)
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1,并写出点A1,B1,C1的坐标.
(2)在y轴上找一点P,使PA+PC最短,并求出P点的坐标.
题组十三 建立坐标系求解线段长
1.如图,在正方形ABCD中,AB=6,点E是BA延长线上一点,2CF=BF,AE=CF,则线段DG的长是( )
A. B. C. D.
2.如图,边长为6的正方形ABCD中,M为对角线BD上的一点,连接AM并延长交CD于点P,若PM=PC,则AM的长为( )
A.3(﹣1) B.3(3﹣2) C.6(﹣1) D.6(3﹣2)
3.课题学习:用函数模型解几何题.
(1)方法体会:如图1,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF与CG的交点,那么EH的长是多少?
下面让我们一起来用函数模型来解这个题目,要好好体会这种解法哟!
解:以点B为坐标原点O,BE、BA所在直线分别为x轴、y轴,建立平面直角坐标系,如图2.以BC长为一个单位长度,则由题意可知点A坐标为(0,1),点F的坐标为(4,3),则直线AF的解析式为 ;请同学们根据点H是AF与CG的交点,求出点H的坐标为 ;进而求得EH的长为 .
(2)解决问题:请仿照上述建立平面直角坐标系的方法解决下面的问题.
如图3,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,四边形DEFG为正方形,D、E分别在边AC、BC上,F、G在边AB上,求DE的长.
题组十四 铅锤法求面积
4.如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=ah,即三角形面积等于水平宽与铅垂高乘积的一半.这个结论是否正确?
5.阅读材料:
如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.
我们可得出一种计算三角形面积的新方法:S△ABC=ah,即三角形面积等于水平宽与铅垂高乘积的一半.
解答下列问题:
已知:直线l1:y=﹣2x+6与x轴交于点A,直线l2:y=x+3与y轴交于点B,直线l1、l2交于点C.
(1)建立平面直角坐标系,画出示意图(无需列表)并求出C点的坐标;
(2)利用阅读材料提供的方法求△ABC的面积.
6.对于某些三角形或四边形,我们可以直接用面积公式或者用割补法来求它们的面积.下面我们再研究一种求某些三角形或四边形面积的新方法:
如图1,2所示,分别过三角形或四边形的顶点A,C作水平线的铅垂线l1,l2,l1,l2之间的距离d叫做水平宽;如图1所示,过点B作水平线的铅垂线交AC于点D,称线段BD的长叫做这个三角形的铅垂高;如图2所示,分别过四边形的顶点B,D作水平线l3,l4,l3,l4之间的距离h叫做四边形的铅垂高.
【结论提炼】
容易证明:“三角形的面积等于水平宽与铅垂高乘积的一半”,即“S=dh”
【结论应用】
为了便于计算水平宽和铅垂高,我们不妨借助平面直角坐标系.
已知:如图3,点A(﹣5,2),B(5,0),C(0,5),则△ABC的水平宽为10,铅垂高为 ,所以△ABC面积的大小为 .
【再探新知】
三角形的面积可以用“水平宽与铅垂高乘积的一半”来求,那四边形的面积是不是也可以这样求呢?带着这个问题,我们进行如下探索:
(1)在图4所示的平面直角坐标系中,取A(﹣4,2),B(1,5),C(4,1),D(﹣2,﹣4)四个点,得到四边形ABCD.运用“水平宽与铅垂高乘积的一半”进行计算得到四边形ABCD面积的大小是 ;用其它的方法进行计算得到其面积的大小是 ,由此发现:用“S=dh”这一方法对求图4中四边形的面积 .(填“适合”或“不适合”)
(2)在图5所示的平面直角坐标系中,取A(﹣5,2),B(1,5),C(4,2),D(﹣2,﹣3)四个点,得到了四边形ABCD.运用“水平宽与铅垂高乘积的一半”进行计算得到四边形ABCD面积的大小是 ,用其它的方法进行计算得到面积的大小是 ,由此发现:用“S=dh”这一方法对求图5中四边形的面积 .(“适合”或“不适合”)
(3)在图6所示的平面直角坐标系中,取A(﹣4,2),B(1,5),C(5,1),D(1,﹣5)四个点,得到了四边形ABCD.通过计算发现:用“S=dh”这一方法对求图6中四边形的面积 .(填“适合”或“不适合”)
【归纳总结】我们经历上面的探索过程,通过猜想、归纳,验证,便可得到:当四边形满足某些条件时,可以用“S=dh”来求面积.那么,可以用“S=dh”来求面积的四边形应满足的条件是: .
题组十五 中点坐标公式
7.探究:
小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用图①得到结论:.他还利用图②证明了线段P1P2的中点P(x,y)的坐标公式:,.
(1)请你帮小明写出中点坐标公式的证明过程.
运用:
(2)已知点M(2,﹣1),N(﹣3,5),求线段MN的长度;
(3)请直接写出以点A(2,2),B(﹣2,0),C(3,﹣1),D为顶点的平行四边形顶点D的坐标.
8.如图1:在△ABC中,
(1)利用尺规作图,做出这个三角形的一条中位线DE,(要求:点D在AB上,点E在AC上;)
(2)直角坐标系的建立,在代数和几何之间架起了一座桥梁,用代数的方法解决几何问题:某数学小组在自主学习时了解了三角形的中位线及相关的定理,在学习了相关知识后,该小组同学深入思考,利用中点坐标公式,给出了三角形中位线定理的另外一种证明方法.该数学小组建立如图2所示的直角坐标系,已知点D,E分别是AB,AC边的中点,不妨设点A(a,b),点C(c,0)(c>0).请你利用该数学学习小组的思路证明DE∥BC且DE=BC.(提示:中点坐标公式,A(x1,y1),B(x2,y2),则A,B中点坐标为(,)
(3)如图3:在△ABC中,∠ACB=90°,AC=3,BC=6,延长AC至点D,DE⊥AD,连接EC并延长AB边于点F,若2CD+DE=6,则EF是否存在最小值,若存在求出最小值,若不存在,请说明理由.
9.预备知识:(1)线段中点坐标公式:在平面直角坐标系中,已知A(x1,y1),B(x2,y2),设点M为线段AB的中点,则点M的坐标为.
①设A(1,2),B(5,0),点M为线段AB的中点,则点M的坐标为 .
②设线段CD的中点为点N,其坐标为(3,2),若端点C的坐标为(7,3),则端点D的坐标为 .
(2)如图,四边形ABCD中,AD∥BC,点E为DC的中点,连结AE并延长交BC的延长线于点F.求证:S四边形ABCD=S△ABF.(S表示面积)
10.知识储备
如图①,点E、F分别是y=3和y=﹣1上的动点,则EF的最小值是 ;
方法储备
直角坐标系的建立,在代数和几何之间架起了一座桥梁,用代数的方法解决几何问题:某数学小组在自主学习时了解了三角形的中位线及相关的定理,在学习了《坐标与位置)后,该小组同学深入思考,利用中点坐标公式,给出了三角形中位线定理的一种证明方法.如图②,在△ABC中,点D,E分别是AB,AC边的中点,DE称为△ABC的中位线,则DE∥BC且DE=BC.该数学小组建立如图③的直角坐标系,设点A(a,b),点C(c,0)(c>0).请你利用该数学学习小组的思路证明DE∥BC且DE=BC.(提示:中点坐标公式,A(x1,y1),B(x2,y2),则A,B中点坐标为(,))
综合应用
结合上述知识和方法解决问题,如图④,在△ABC中,∠ACB=90°,AC=3,BC=6,延长AC至点 D.DE⊥AD,连接EC并延长交AB边于点F.若2CD+DE=6,则EF是否存在最小值,若存在,求出最小值;若不存在,请说明理由.
题组十六 两点间的距离公式
11.先阅读下列一段文字,再解答问题
已知在平面内有两点P1(x1,y1),P2(x2,y2),其两点间的距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
如图1:平面直角坐标系中,点A(2,3),B(3,﹣1),直线AB交x轴于点C,连接OA,OB.
①直接写出OA,OB的值;用两点间的距离公式求出线段AB的长度.
②试求点C的坐标和三角形AOB的面积.
③如图2:如果点D在平行x轴的直线上,连接OD,DC,三角形ODC的面积比三角形OAC大1,请直接写出点D的纵坐标.
12.先阅读下列一段文字,再回答问题:
已知平面内两点P1(x1,y1)、P2(x2,y2),这两点间的距离同时当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)已知点M(2,3)、N(4,2),则M、N两点间的距离为 ;已知点E、F在平行于x轴的直线上,点E的横坐标为7,点F的横坐标为5,则E、F两点间的距离 ;
(2)已知一个三角形的各顶点坐标分别为A(﹣2,1)、B(2,4)、C(5,0),你能判定此三角形的形状吗?请说明理由.
(3)在(2)的条件下,在x轴上有一点P,若PA+PB的值最小,请找出点P(不求坐标,画出图形即可),求出PA+PB的最小值.
13.如图①,我们在“格点”直角坐标系上可以清楚看到:要找AB或DE的长度,显然是转化为求Rt△ABC或Rt△DEF的斜边长.下面以求DE为例来说明如何解决:
从坐标系中发现:D(﹣7,5),E(4,﹣3),
所以DF=|5﹣(﹣3)|=8,
EF=|4﹣(﹣7)|=11,
所以由勾股定理可得,.
解决以下问题:
(1)图①中:AC= ,BC= ,所以AB= ;
(2)在图②中,设A(x1,y1),B(x1,y2),试用x1,x2,y1,y2表示,AC= ,BC= ,所以AB= ;
由此得到平面直角坐标系内任意两点间的距离公式.请用此公式解决问题:
(3)在平面直角坐标系中的两点A(﹣1,3),B(4,1),P为x轴上任一点,求PA+PB的最小值;
(4)应用平面内两点间的距离公式,求代数式的最小值为: .(直接写出答案)
14.【阅读与应用】如图1已知平面内两点A(x1,y1)、B(x2,y2),过这两点分别作垂直于x轴和y轴的虚线相交于点M,则BM间的距离为|x1﹣x2|,则BM2=(x1﹣x2)2,同理AM间的距离为|y1﹣y2|,则,由勾股定理得:AB2=BM2+AM2,即:,则平面内任意两点间的距离公式为AB=.
(1)如图2,已知点A(4,5)、B(1,1),试利用两点间的距离公式求A、B两点间的距离?
(2)课本阅读:如果一个三角形的三边长分别为a,b,c,记,那么这个三角形的面积为,这个公式叫“海伦公式”.
如图3,在(1)的条件下,△ABC中,AB=c,BC=a=7,AC=b=8,试利用“海伦公式”,求△ABC的面积?
(3)如图4,在(2)的条件下,过点C作CD⊥AB,垂足为D,求线段CD的长?
题组一 平面直角坐标系坐标特征
1.下列各点中在第四象限的是( )
A.(﹣3,7) B.(3,﹣7) C.(3,7) D.(﹣3,﹣7)
2.在平面直角坐标系中,若点P(m,m﹣n)与点Q(2,1)关于原点对称,则点M(m,n)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.平面直角坐标系中,点A在第四象限,点A到x轴的距离为2,到y轴的距离为3,则点A的坐标为( )
A.(2,﹣3) B.(﹣3,2) C.(3,﹣2) D.(﹣2,3)
4.下列说法正确的是( )
A.点(1,﹣a2)在第四象限 B.若ab=0,则P(a,b)在坐标原点
C.点P在第二象限,且点P到x轴的距离为2,点P到y轴的距离为3,则点P的坐标为(﹣3,2)
D.在平面直角坐标系中,若点A的坐标为(﹣1,﹣2),且AB平行于x轴,AB=5,则点B的坐标为(4,﹣2)
5.下列说法不正确的是( )
A.在x轴上的点的纵坐标为0 B.点P(﹣1,3)到y轴的距离是1
C.若xy<0,x﹣y>0,那么点Q(x,y)在第四象限 D.点A(﹣a2﹣1,|b|)一定在第二象限
题组二 基本对称变换
6.在平面直角坐标系中,坐标为(a,b)的点关于x轴对称的点的坐标为( )
A.(a,﹣b) B.(b,a) C.(﹣a,b) D.(﹣b,﹣a)
7.点A(1,﹣2)经过某种图形变化后得到点A′(2,1),这种图形变化可以是( )
A.绕原点逆时针旋转90° B.绕原点顺时针旋转90° C.关于x轴对称 D.关于y轴对称
8.点A(2023,﹣2024)关于y轴对称的点的坐标为( )
A.(﹣2024,2023) B.(2023,﹣2024) C.(﹣2023,﹣2024) D.(2023,2024)
9.在直角坐标系中,已知点A(2+a,b﹣2),B(b,1)关于原点对称,则a,b的值是( )
A.a=0,b=0 B.a=﹣3,b=1 C.a=1,b=﹣3 D.a=5,b=3
10.若点A(a+b,﹣1)与点B(5,a﹣b) 关于原点对称,则点P(a,b)的坐标是( )
A.(2,3) B.(3,2) C.(﹣2,﹣3) D.(﹣3,﹣2)
题组三 关于x=a对称
11.平面直角坐标系中,已知点P(a,﹣3)在第四象限,则点P关于直线x=2对称的点的坐标是( )
A.(a,1) B.(﹣a+2,﹣3) C.(﹣a+4,﹣3) D.(﹣a,﹣3)
12.在平面直角坐标系中,点P(﹣2,3)关于直线x=1的对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
13.在平面直角坐标系中,已知A(4,3),A′与A关于直线x=1轴对称,则A′的坐标为( )
A.(﹣4,3) B.(4,﹣1) C.(﹣2,3) D.(4,﹣3)
14.平面直角坐标系中,已知点P(a,3)在第二象限,则点P关于直线m(直线m上各点的横坐标都是2)对称的点的坐标是( )
A.(﹣a,3) B.(a,﹣3) C.(﹣a+2,3) D.(﹣a+4,3)
15.在平面直角坐标系中,已知点P(a2+2,5),则点P关于直线m(直线m上各点的横坐标都为﹣2)对称点的坐标是( )
A.(﹣a2+6,5) B.(﹣a2﹣6,5) C.(a2﹣6,5) D.(﹣a2+4,5)
题组四 关于y=b对称
16.已知A(﹣4,1),那么A点关于直线y=﹣1对称的点的坐标为( )
A.(4,1) B.(﹣4,﹣1) C.(﹣4,﹣3) D.(﹣4,3)
17.如图点A和B关于直线y=1对称,已知点A坐标是(4,4),则点B的坐标是( )
18题图
A.(4,﹣4) B.(4,﹣2) C.(﹣2,4) D.(﹣4,2)
18.点P(﹣2,1)与点Q(a,b)关于直线y=﹣1对称,则点Q的坐标为( )
A.(﹣2,﹣3) B.(﹣2,﹣1) C.(﹣2,﹣2) D.(﹣2,﹣4)
19.在直角坐标系中,点A与点C关于直线y=2成轴对称,已知点A的坐标是(5,5),则点C的坐标是( )
A.(5,﹣5) B.(5,﹣1) C.(﹣2,5) D.(﹣5,1)
20.若点P(﹣2,a),Q(b,3),且PQ∥x轴,则a,b的值为( )
A.a=3,b≠2 B.a=3,b≠﹣2 C.a≠﹣3,b=2 D.a≠﹣3,b=﹣2
题组五 一三象限角平分线上的点
21.在平面直角坐标系中,点P(2m+3,3m﹣1)在第一三象限角平分线上,则点P的坐标为( )
A.(4,4) B.(3,3) C.(11,11) D.(﹣11,﹣11)
22.已知点P(5﹣a,2a﹣1)在一、三象限的角平分线上,则a的值为( )
A.﹣1 B.0 C.1 D.2
23.已知点P(a,2a+1)在一、三象限的角平分线上,则a的值为( )
A.﹣1 B.0 C.1 D.2
24.已知点P(a,1)在一、三象限的角平分线上,则a的值为( )
A.﹣1 B.0 C.1 D.2
25.已知点P(a,2a﹣1)在一、三象限的角平分线上,则a的值为( )
A.﹣1 B.0 C.1 D.2
题组六 二四象限角平分线上的点
26.已知点A(2a+1,5a﹣2)在第一、三象限的角平分线上,点B(2m+7,m﹣1)在二、四象限的角平分线上,则( )
A.a=1,m=﹣2 B.a=1,m=2 C.a=﹣1,m=﹣2 D.a=﹣1,m=2
27.已知点P(a,b)在第一、三或二、四象限坐标轴夹角的角平分线上,则有( )
A.a+b=0 B.a﹣b=0 C.a2﹣b2=0 D.a2+b2=0
28.点P(3﹣2x,5﹣x)在二、四象限的角平分线上,则x=( )
A. B.2 C. D.﹣2
29.点P(2x,y)在二、四象限的角平分线上,则( )
A.2x=y B.2x=﹣y C.﹣x=y D.|﹣2x|=y
30.若x+y=0,则点P(x,y)的位置是( )
A.一、三象限的角平分线上 B.二、四象限的角平分线上
C.二、三象限的角平分线上 D.一、四象限的角平分线上
题组七 关于一三象限角平分线对称
31.如图,在平面直角坐标系中,线段OA与OA′关于一、三象限的角平分线对称,已知点A的坐标为(2,1),则点A′的坐标为 .
32题图34题图
32.(1)如图,点P(﹣2,1)与点Q(a,b)关于直线l(y=﹣1)对称,则a+b= ;
(2)在平面直角坐标系中,点P(﹣3,2)关于第一、三象限角平分线对称的点的坐标是 .
33.点M(﹣1,3)关于第一、三象限的角平分线对称的点的坐标为 .
34.如图,第一、三象限角平分线记为y=x,如点(﹣1,﹣2)关于直线y=x对称点坐标为(﹣2,﹣1),点(a,b)关于y=x对称点的坐标为 .
35.点A(a,b)关于第一、三象限的角平分线(y=x)的对称点的坐标为A4 .
题组八 关于二四象限角平分线对称
36.已知点A(﹣2,3).若A、B两点关于x轴对称,则B的坐标为 ;若A、B两点关于二、四象限角平分线对称,则B的坐标为 .
37.已知点A(m,﹣3),B(2,n).若点A、B关于y轴对称,则m= ,n= ;若A、B在二、四象限的角平分线上,则m= ,n= .
38.点P(a,b)关于二四象限的角平分线的对称点表示为 .
39.点P(2,1)关于y=﹣x对称的点的坐标是 .
40.在平面直角坐标系中,点P(﹣4,﹣2)关于直线y=﹣x对称的点P′的坐标为 .
题组九 点的平移变换
41.在平面直角坐标系中,线段AB两个端点A(1,2),B(7,5).将线段AB平移后,点A的新坐标为(﹣6,﹣3),则点B的新坐标为 .
42.直角坐标系中,已知线段AB的两个端点分别是A(3,﹣2),B(1,1),将线段AB平移后得到线段A1B1.若点A1的坐标为(﹣1,2),则点B1的坐标为 .
43.在平面直角坐标系中,已知线段AB的两个端点分别是A(1,2),B(2,0),将线段AB平移后得到线段CD,其中,点A的对应点为点C,若C(3,a),D(b,1),则a﹣b的值为 .
44.线段AB的两个端点的坐标为A(m,2),B(3,5),将线段AB平移后得线段A′B′,其中A′(0,3),B′(6,n),则线段AB上的点C(﹣1,3)平移后的坐标是 .
45.如图,在平面直角坐标系中,点A,B的坐标分别为(﹣2,0)和(0,1),将线段AB平移,若平移后A,B的对应点为C(﹣1,m),D(n,3),则m+n的值是
题组十 点的规律变换
46.如图,在平面直角坐标系中,将等边△OAB绕点A旋转180°得到△O1AB,再将ΔO1AB1绕点O1旋转180°得到△O1A1B2,再将△O1A1B2绕点A1旋转180°得到△O2A1B,…,按此规律进行下去,若点B的坐标为(﹣2,0),则点B2024的坐标为 .
47题图 48题图
47.如图所示,长方形ABCD的两边BC、CD分别在x轴、y轴上,点C与原点重合,点A的坐标为(2,3),将长方形ABCD沿x轴无滑动向右翻滚,经过一次翻滚,点A的对应点记为A1;经过第二次翻滚,点A的对应点记为A2;……依次类推,经过第2024次翻滚,点A的对应点A2024的坐标为 .
48.如图,在平面直角坐标系xOy中,已知抛物线y=﹣x(x﹣3)(0≤x≤3)在x轴上方的部分,记作C1,它与x轴交于点O,A1,将C1绕点A1旋转180°得C2,C2与x轴交于另一点A2.请继续操作并探究:将C2绕点A2旋转180°得C3,与x轴交于另一点A3;将C3绕点A2旋转180°得C4,与x轴交于另一点A4,这样依次得到x轴上的点A1,A2,A3,…,An,…,及抛物线C1,C2,…, n,….则点A4的坐标为 ; n的顶点坐标为 (n为正整数,用含n的代数式表示).
49.已知:如图,直线l:y=﹣x﹣1,一组可由平移变换得到的抛物线的顶点为B1,B2、B3、…Bn(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是A1(x1,0),A2(x2,0),A3(x3,0),…An+1(xn+1,0)(n为正整数),其中x1=0,x2=2,则x3= ;B8的坐标为 .
50.在平面直角坐标系中,△OAB的位置如图所示,将△OAB绕点O顺时针旋转90°得△OA1B1;再将△OA1B1绕点O顺时针旋转90°得△OA2B2;再将△OA2B2绕点O顺时针旋转90°得△OA3B3;……依此类推,第2021次旋转得到△OA2021B2021,则顶点A的对应点A2021的坐标是 .
题组十一 坐标系内任意三点求面积
51.阅读以下材料,并解决问题:
小明遇到一个问题:在平面直角坐标系xOy中,点A(1,4),B(5,2),求△OAB的面积.
小明用割补法解决了此问题,如图,过点A作AM⊥x轴于点M,过点B作BN⊥x轴于点N,则S△OAB=S△OAM+S梯形AMNB﹣S△OBN=×1×4+(2+4)(5﹣1)﹣×5×2=9.
解决问题后小明又思考,如果将问题一般化是否会有好的结论.于是它首先研究了点A,B在第一象限内的一种情形:如图,点A(x1,y1),B(x2,y2),其中x1<x2,y1>y2.
(1)请你帮助小明求出这种情形下△OAB的面积.(用含x1,x2,y1,y2的式子表示)
(2)小明继续研究发现,只要将(1)中求得的式子再取绝对值就可以得到第一象限内任意两点A,B(点O,A,B不共线)与坐标原点O构成的三角形△OAB的面积公式,请利用此公式解决问题:已知点A(a,a+2),B(x,y)在第一象限内,探究是否存在点B,使得对于任意的a>0,都有S△OAB=2?若存在,求出点B的坐标;若不存在,说明理由.
52.如图,在△AOB中,A、B两点的坐标分别为(2,4)和(6,2),求△AOB的面积.
53.如图,三角形AOB中,A、B两点的坐标分别为(2,4)、(6,2).
(1)求三角形AOB的面积;
(2)若点P的横坐标为2,使得三角形ABP的面积为6,求点P的坐标.
54.△ABC的顶点坐标分别是A(﹣1,2),B(﹣3,0),C(2,0),求△ABC的面积.
55.如图,已知:A(2,0),B(0,﹣2),点P(a,1),S△PAB>5,求a的取值范围.
题组十二 作图--对称变换
56.在正方形网格中,每个小正方形的边长为1,点A(﹣4,5),C(﹣1,3),A1(4,5),B1(2,1),△ABC与△A1B1C1关于某直线成轴对称.
(1)在网格内完善平面直角坐标系;
(2)点B坐标是 ,点C1坐标是 ;
(3)求△A1B1C1的面积.
57.如图,在平面直角坐标系中,每个小正方形的边长均为1,请回答下列问题:
(1)点A在第 象限,它的坐标是 ;
(2)点B在第 象限,它的坐标是 ;
(3)将△AOB的每个顶点的横坐标保持不变,纵坐标都乘以﹣1,再顺次连接这些点,所得的图形与△AOB关于 轴对称.
58.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别是A(2,﹣1),B(1,﹣2),C(3,﹣3).
(1)请画出与△ABC关于y轴对称的△A1B1C1,并写出点C1的坐标;
(2)在(1)的条件下,画出与△A1B1C1关于直线l对称的△A2B2C2;
(3)在(2)的条件下,若点P1(m,n)在△A1B1C1的内部,则点P1在△A2B2C2中对应点P2的坐标是 .
59.如图,在平面直角坐标系中,已知点A(﹣4,1);B(1,1),C(﹣3,3).
(1)判断△ABC的形状,并说明理由;
(2)若点C关于直线AB的对称点为点D,则点D的坐标为 ;
(3)连接CD,BD,则△BCD的周长为 .
60.如图已知平面直角坐标系中A(﹣1,3),B(2,0),C(﹣3,﹣1)
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1,并写出点A1,B1,C1的坐标.
(2)在y轴上找一点P,使PA+PC最短,并求出P点的坐标.
题组十三 建立坐标系求解线段长
1.如图,在正方形ABCD中,AB=6,点E是BA延长线上一点,2CF=BF,AE=CF,则线段DG的长是( )
A. B. C. D.
2.如图,边长为6的正方形ABCD中,M为对角线BD上的一点,连接AM并延长交CD于点P,若PM=PC,则AM的长为( )
A.3(﹣1) B.3(3﹣2) C.6(﹣1) D.6(3﹣2)
3.课题学习:用函数模型解几何题.
(1)方法体会:如图1,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF与CG的交点,那么EH的长是多少?
下面让我们一起来用函数模型来解这个题目,要好好体会这种解法哟!
解:以点B为坐标原点O,BE、BA所在直线分别为x轴、y轴,建立平面直角坐标系,如图2.以BC长为一个单位长度,则由题意可知点A坐标为(0,1),点F的坐标为(4,3),则直线AF的解析式为 ;请同学们根据点H是AF与CG的交点,求出点H的坐标为 ;进而求得EH的长为 .
(2)解决问题:请仿照上述建立平面直角坐标系的方法解决下面的问题.
如图3,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,四边形DEFG为正方形,D、E分别在边AC、BC上,F、G在边AB上,求DE的长.
题组十四 铅锤法求面积
4.如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=ah,即三角形面积等于水平宽与铅垂高乘积的一半.这个结论是否正确?
5.阅读材料:
如图,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.
我们可得出一种计算三角形面积的新方法:S△ABC=ah,即三角形面积等于水平宽与铅垂高乘积的一半.
解答下列问题:
已知:直线l1:y=﹣2x+6与x轴交于点A,直线l2:y=x+3与y轴交于点B,直线l1、l2交于点C.
(1)建立平面直角坐标系,画出示意图(无需列表)并求出C点的坐标;
(2)利用阅读材料提供的方法求△ABC的面积.
6.对于某些三角形或四边形,我们可以直接用面积公式或者用割补法来求它们的面积.下面我们再研究一种求某些三角形或四边形面积的新方法:
如图1,2所示,分别过三角形或四边形的顶点A,C作水平线的铅垂线l1,l2,l1,l2之间的距离d叫做水平宽;如图1所示,过点B作水平线的铅垂线交AC于点D,称线段BD的长叫做这个三角形的铅垂高;如图2所示,分别过四边形的顶点B,D作水平线l3,l4,l3,l4之间的距离h叫做四边形的铅垂高.
【结论提炼】
容易证明:“三角形的面积等于水平宽与铅垂高乘积的一半”,即“S=dh”
【结论应用】
为了便于计算水平宽和铅垂高,我们不妨借助平面直角坐标系.
已知:如图3,点A(﹣5,2),B(5,0),C(0,5),则△ABC的水平宽为10,铅垂高为 ,所以△ABC面积的大小为 .
【再探新知】
三角形的面积可以用“水平宽与铅垂高乘积的一半”来求,那四边形的面积是不是也可以这样求呢?带着这个问题,我们进行如下探索:
(1)在图4所示的平面直角坐标系中,取A(﹣4,2),B(1,5),C(4,1),D(﹣2,﹣4)四个点,得到四边形ABCD.运用“水平宽与铅垂高乘积的一半”进行计算得到四边形ABCD面积的大小是 ;用其它的方法进行计算得到其面积的大小是 ,由此发现:用“S=dh”这一方法对求图4中四边形的面积 .(填“适合”或“不适合”)
(2)在图5所示的平面直角坐标系中,取A(﹣5,2),B(1,5),C(4,2),D(﹣2,﹣3)四个点,得到了四边形ABCD.运用“水平宽与铅垂高乘积的一半”进行计算得到四边形ABCD面积的大小是 ,用其它的方法进行计算得到面积的大小是 ,由此发现:用“S=dh”这一方法对求图5中四边形的面积 .(“适合”或“不适合”)
(3)在图6所示的平面直角坐标系中,取A(﹣4,2),B(1,5),C(5,1),D(1,﹣5)四个点,得到了四边形ABCD.通过计算发现:用“S=dh”这一方法对求图6中四边形的面积 .(填“适合”或“不适合”)
【归纳总结】我们经历上面的探索过程,通过猜想、归纳,验证,便可得到:当四边形满足某些条件时,可以用“S=dh”来求面积.那么,可以用“S=dh”来求面积的四边形应满足的条件是: .
题组十五 中点坐标公式
7.探究:
小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用图①得到结论:.他还利用图②证明了线段P1P2的中点P(x,y)的坐标公式:,.
(1)请你帮小明写出中点坐标公式的证明过程.
运用:
(2)已知点M(2,﹣1),N(﹣3,5),求线段MN的长度;
(3)请直接写出以点A(2,2),B(﹣2,0),C(3,﹣1),D为顶点的平行四边形顶点D的坐标.
8.如图1:在△ABC中,
(1)利用尺规作图,做出这个三角形的一条中位线DE,(要求:点D在AB上,点E在AC上;)
(2)直角坐标系的建立,在代数和几何之间架起了一座桥梁,用代数的方法解决几何问题:某数学小组在自主学习时了解了三角形的中位线及相关的定理,在学习了相关知识后,该小组同学深入思考,利用中点坐标公式,给出了三角形中位线定理的另外一种证明方法.该数学小组建立如图2所示的直角坐标系,已知点D,E分别是AB,AC边的中点,不妨设点A(a,b),点C(c,0)(c>0).请你利用该数学学习小组的思路证明DE∥BC且DE=BC.(提示:中点坐标公式,A(x1,y1),B(x2,y2),则A,B中点坐标为(,)
(3)如图3:在△ABC中,∠ACB=90°,AC=3,BC=6,延长AC至点D,DE⊥AD,连接EC并延长AB边于点F,若2CD+DE=6,则EF是否存在最小值,若存在求出最小值,若不存在,请说明理由.
9.预备知识:(1)线段中点坐标公式:在平面直角坐标系中,已知A(x1,y1),B(x2,y2),设点M为线段AB的中点,则点M的坐标为.
①设A(1,2),B(5,0),点M为线段AB的中点,则点M的坐标为 .
②设线段CD的中点为点N,其坐标为(3,2),若端点C的坐标为(7,3),则端点D的坐标为 .
(2)如图,四边形ABCD中,AD∥BC,点E为DC的中点,连结AE并延长交BC的延长线于点F.求证:S四边形ABCD=S△ABF.(S表示面积)
10.知识储备
如图①,点E、F分别是y=3和y=﹣1上的动点,则EF的最小值是 ;
方法储备
直角坐标系的建立,在代数和几何之间架起了一座桥梁,用代数的方法解决几何问题:某数学小组在自主学习时了解了三角形的中位线及相关的定理,在学习了《坐标与位置)后,该小组同学深入思考,利用中点坐标公式,给出了三角形中位线定理的一种证明方法.如图②,在△ABC中,点D,E分别是AB,AC边的中点,DE称为△ABC的中位线,则DE∥BC且DE=BC.该数学小组建立如图③的直角坐标系,设点A(a,b),点C(c,0)(c>0).请你利用该数学学习小组的思路证明DE∥BC且DE=BC.(提示:中点坐标公式,A(x1,y1),B(x2,y2),则A,B中点坐标为(,))
综合应用
结合上述知识和方法解决问题,如图④,在△ABC中,∠ACB=90°,AC=3,BC=6,延长AC至点 D.DE⊥AD,连接EC并延长交AB边于点F.若2CD+DE=6,则EF是否存在最小值,若存在,求出最小值;若不存在,请说明理由.
题组十六 两点间的距离公式
11.先阅读下列一段文字,再解答问题
已知在平面内有两点P1(x1,y1),P2(x2,y2),其两点间的距离公式为P1P2=,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
如图1:平面直角坐标系中,点A(2,3),B(3,﹣1),直线AB交x轴于点C,连接OA,OB.
①直接写出OA,OB的值;用两点间的距离公式求出线段AB的长度.
②试求点C的坐标和三角形AOB的面积.
③如图2:如果点D在平行x轴的直线上,连接OD,DC,三角形ODC的面积比三角形OAC大1,请直接写出点D的纵坐标.
12.先阅读下列一段文字,再回答问题:
已知平面内两点P1(x1,y1)、P2(x2,y2),这两点间的距离同时当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)已知点M(2,3)、N(4,2),则M、N两点间的距离为 ;已知点E、F在平行于x轴的直线上,点E的横坐标为7,点F的横坐标为5,则E、F两点间的距离 ;
(2)已知一个三角形的各顶点坐标分别为A(﹣2,1)、B(2,4)、C(5,0),你能判定此三角形的形状吗?请说明理由.
(3)在(2)的条件下,在x轴上有一点P,若PA+PB的值最小,请找出点P(不求坐标,画出图形即可),求出PA+PB的最小值.
13.如图①,我们在“格点”直角坐标系上可以清楚看到:要找AB或DE的长度,显然是转化为求Rt△ABC或Rt△DEF的斜边长.下面以求DE为例来说明如何解决:
从坐标系中发现:D(﹣7,5),E(4,﹣3),
所以DF=|5﹣(﹣3)|=8,
EF=|4﹣(﹣7)|=11,
所以由勾股定理可得,.
解决以下问题:
(1)图①中:AC= ,BC= ,所以AB= ;
(2)在图②中,设A(x1,y1),B(x1,y2),试用x1,x2,y1,y2表示,AC= ,BC= ,所以AB= ;
由此得到平面直角坐标系内任意两点间的距离公式.请用此公式解决问题:
(3)在平面直角坐标系中的两点A(﹣1,3),B(4,1),P为x轴上任一点,求PA+PB的最小值;
(4)应用平面内两点间的距离公式,求代数式的最小值为: .(直接写出答案)
14.【阅读与应用】如图1已知平面内两点A(x1,y1)、B(x2,y2),过这两点分别作垂直于x轴和y轴的虚线相交于点M,则BM间的距离为|x1﹣x2|,则BM2=(x1﹣x2)2,同理AM间的距离为|y1﹣y2|,则,由勾股定理得:AB2=BM2+AM2,即:,则平面内任意两点间的距离公式为AB=.
(1)如图2,已知点A(4,5)、B(1,1),试利用两点间的距离公式求A、B两点间的距离?
(2)课本阅读:如果一个三角形的三边长分别为a,b,c,记,那么这个三角形的面积为,这个公式叫“海伦公式”.
如图3,在(1)的条件下,△ABC中,AB=c,BC=a=7,AC=b=8,试利用“海伦公式”,求△ABC的面积?
(3)如图4,在(2)的条件下,过点C作CD⊥AB,垂足为D,求线段CD的长?
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
