河北省邯郸市成安县2023-2024学年八年级上学期期末数学试题(含解析)
文档属性
| 名称 | 河北省邯郸市成安县2023-2024学年八年级上学期期末数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 338.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-21 15:28:14 | ||
图片预览


文档简介
河北省邯郸市成安县2023-2024学年八年级上学期期末数学试题
一、相信你.你会选(1-10每小题3分,11-16每小题2分共42分)
1.下列各组数中都是无理数的为( )
A. B. C. D.
2.下列各式中,正确的是( )
A. B. C. D.
3.一组数据按从小到大排列为3,4,7,x,15,17,若这组数据的中位数为9,则x是( )
A.9 B.10 C.11 D.12
4.已知一个二元一次方程的一个解是,则这个方程可能是( )
A. B. C. D.
5.已知二元一次方程组 ,把②代入①,整理,得( )
A.x﹣2x+1=4 B.x﹣2x﹣1=4 C.x﹣6x﹣3=6 D.x﹣6x+3=4
6.以方程组的解为坐标的点,在平面直角坐标系中的位置是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.据统计,某班7个学习小组上周参加“青年大学习”的人数分别为:5,5,6,6,6,7,7,下列说法错误的是( )
A.该组数据的中位数是6 B.该组数据的众数是6
C.该组数据的平均数是6 D.该组数据的方差是6
8.在第60届国际数学奥林匹克比赛中,中国队荣获团体总分第一名.我国参赛选手比赛成绩的方差计算公式为:,下列说法错误的是( ).
A.我国一共派出了6名选手 B.我国参赛选手的平均成绩为38分
C.我国选手比赛成绩的中位数为38 D.我国选手比赛成绩的团体总分为228分
9.如图,直线AB,CD,相交于点O,∠MON=90°.∠BON比∠MOA多10°.求∠BON,∠MOA的度数若设∠BON=x°,∠MOA=y°.可列方程组为( )
A. B. C. D.
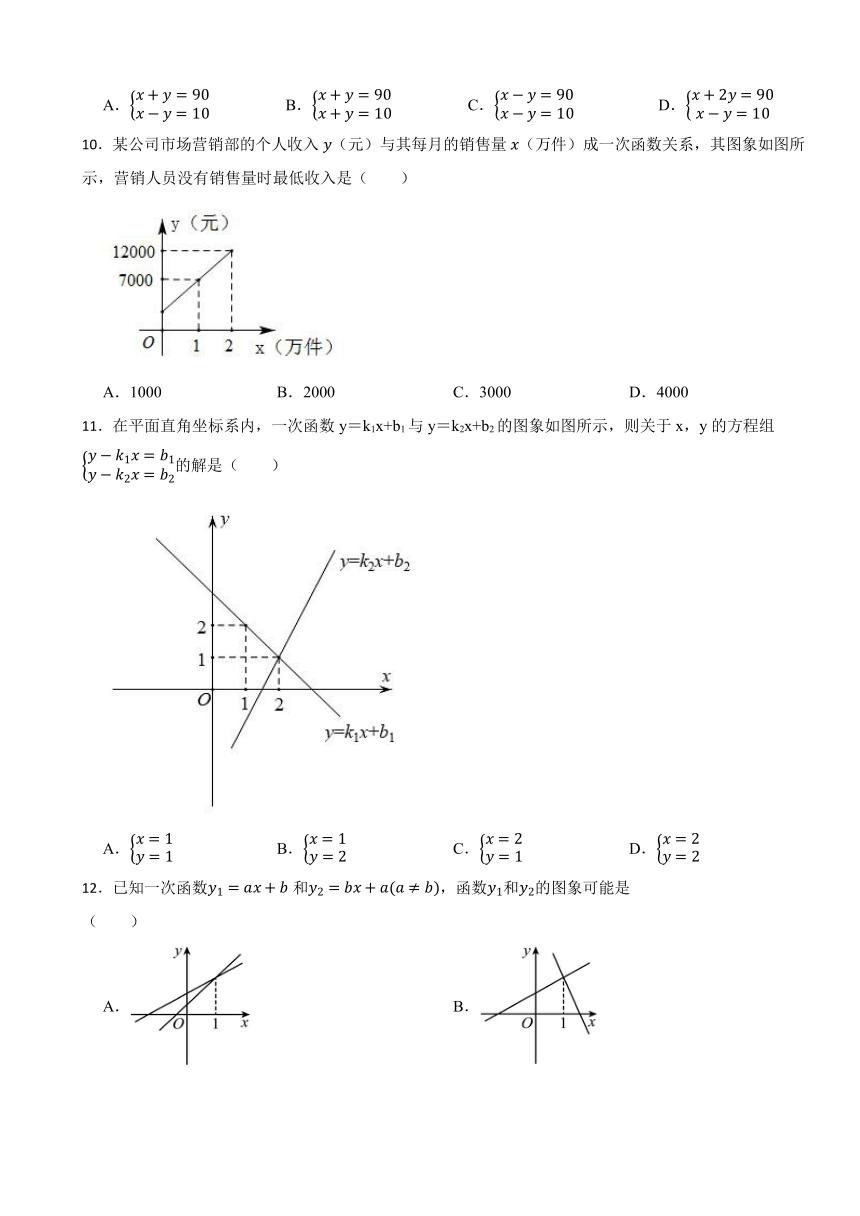
10.某公司市场营销部的个人收入(元)与其每月的销售量(万件)成一次函数关系,其图象如图所示,营销人员没有销售量时最低收入是( )
A.1000 B.2000 C.3000 D.4000
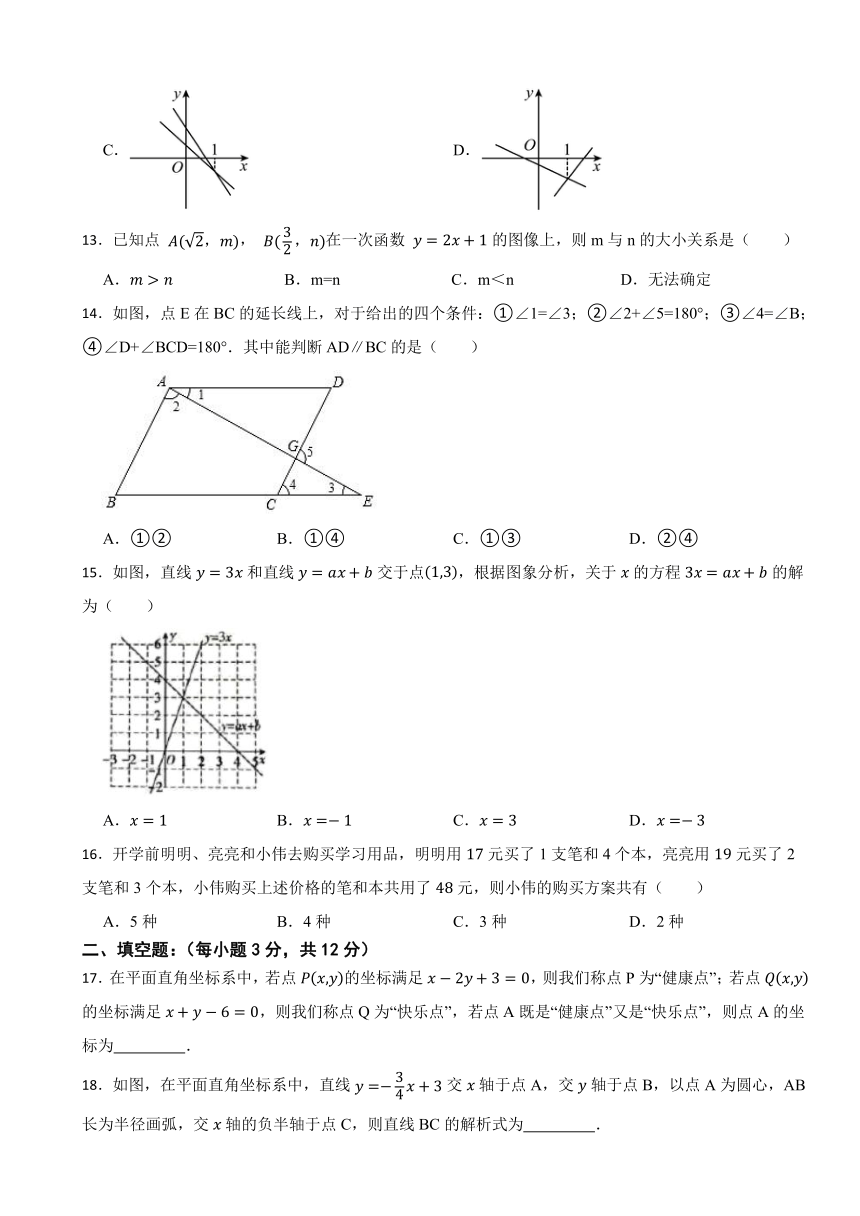
11.在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组的解是( )
A. B. C. D.
12.已知一次函数和,函数和的图象可能是 ( )
A. B.
C. D.
13.已知点
,
在一次函数
的图像上,则m与n的大小关系是( )
A. B.m=n C.m<n D.无法确定
14.如图,点E在BC的延长线上,对于给出的四个条件:①∠1=∠3;②∠2+∠5=180°;③∠4=∠B;④∠D+∠BCD=180°.其中能判断AD∥BC的是( )
A.①② B.①④ C.①③ D.②④
15.如图,直线和直线交于点,根据图象分析,关于的方程的解为( )
A. B. C. D.
16.开学前明明、亮亮和小伟去购买学习用品,明明用元买了1支笔和4个本,亮亮用元买了2支笔和3个本,小伟购买上述价格的笔和本共用了元,则小伟的购买方案共有( )
A.5种 B.4种 C.3种 D.2种
二、填空题:(每小题3分,共12分)
17.在平面直角坐标系中,若点的坐标满足,则我们称点P为“健康点”;若点的坐标满足,则我们称点Q为“快乐点”,若点A既是“健康点”又是“快乐点”,则点A的坐标为 .
18.如图,在平面直角坐标系中,直线交轴于点A,交轴于点B,以点A为圆心,AB长为半径画弧,交轴的负半轴于点C,则直线BC的解析式为 .
19.某校规定学生的期末学科成绩由三部分组成,将课堂、作业和考试三项得分按1:3:6的权重确定每个人的期末成绩.小明同学本学期数学这三项得分分别是:课堂98分,作业95分,考试85分,那么小明的数学期末成绩是 分.
20.如图1,已知直线,且和分别相交于A,B两点,和分别交于C,D两点,点P在线段上若,则 .
三、简答题:(本题共46分)
21.计算下列各题:
(1);
(2).
22.在甘肃抗震救灾捐款活动中,某市振兴中学某班的学生对本校学生自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为,又知此次调查中捐款25元和30元的学生一共42人.
(1)他们一共调查了多少人?
(2)这组数据的众数,中位数各是多少?
23.列方程(组)解应用题:
汾河古称“汾”,又称汾水,是山西最大的河流,被山西人称为“母亲河”,对山西省的历史文化有着深远的影响.为打造“一川清水、两岸锦绣”的生态环境,现将一段长为的汾河两岸绿化任务交由甲、乙两个工程队先后接力完成.甲工程队每天绿化,乙工程队每天绿化,共用时天.
根据以上信息,小敏和小颖由自己的设想方案分别列出了尚不完整的方程组:
小敏:
小颖:
(1)请你在方框中补全小敏和小颖所列的方程组;
(2)根据小敏和小颖所列的方程组,分别指出未知数,表示的实际意义:
小敏:表示_____________,表示____________;
小颖:表示____________,表示______________;
(3)请你选择一种方案,求甲、乙两工程队分别绿化河岸多少米?
24.如图,点A、B分别在射线上运动(不与点O重合).
(1)如图1,若的平分线交于点C,则 ;
(2)如图2,若的平分线交于点C,则 ;
(3)如图2,若的外角的平分线交于点D,求与之间的数量关系,并求出的度数.
25.甲乙两地分别对本地各40万人接种某种疫苗,甲地在前期完成5万人接种后,甲、乙两地同时以相同速度接种,甲地经过a天后接种人数达到25万人,由于情况变化,接种速度放缓,结果100天完成接种任务,乙地80天完成接种任务,在某段时间内,甲、乙两地的接种人数y(万人)与各自接种时间x(天)之间的关系如图所示.
(1)乙地每天接种_________万人,
(2)当甲地接种速度放缓后,求y关于x的函数表达式;
(3)当乙地完成接种任务时,求甲地未接种疫苗的人数.
答案解析部分
1.【答案】C
【知识点】无理数的概念;求算术平方根
【解析】【解答】解:A、∵中的0.07,不是无理数,∴A错误;
B、∵中的不是无理数,∴B错误;
C、∵中的都是无理数,∴C正确;
D,∵中的不是无理数,∴D错误.
故答案为:C.
【分析】利用无理数的定义(无限不循环小数称为无理数)逐个分析判断求解即可.
2.【答案】D
【知识点】立方根及开立方;二次根式的性质与化简
【解析】【解答】解:A、原式 ,不符合题意;
B、原式 ,不符合题意;
C、原式 ,不符合题意;
D、原式 ,符合题意,
故答案为:D.
【分析】利用指数幂的运算性质即可得出答案。
3.【答案】C
【知识点】中位数
【解析】【解答】解:由题意得,(7+x)÷2=9,
解得:x=11.
故答案为:C.
【分析】根据中位数为中间两个数据的平均数可得(7+x)÷2=9,计算即可.
4.【答案】B
【知识点】二元一次方程的解
【解析】【解答】解:A、∵将代入,等式左右两边不相等,∴A是错误的;
B、∵将代入,等式左右两边相等,∴B是正确的;
C、∵将代入,等式左右两边不相等,∴C是错误的;
D、∵将代入,等式左右两边不相等,∴D错误的;
故答案为:B.
【分析】将分别代入各选项进行计算并判断即可.
5.【答案】D
【知识点】代入消元法解二元一次方程组
【解析】【解答】解: ,
把②代入①得:x﹣3(2x﹣1)=4,
整理,得:x﹣6x+3=4
故答案为:D.
【分析】利用代入消元法求解即可。
6.【答案】B
【知识点】点的坐标与象限的关系;加减消元法解二元一次方程组
【解析】【解答】解:
由,得:,
解得:.
将代入①,得:,
解得:,
∴原方程组的解为,
∴点在平面直角坐标系中的位置是第二象限.
故答案为:B.
【分析】先利用加减消元法的计算方法及步骤求出解集,再利用四个象限点坐标的符号特点(①第一象限(+,+);②第二象限(-,+);③第三象限(-,-);④第四象限(+,-))分析求解即可.
7.【答案】D
【知识点】平均数及其计算;中位数;方差;众数
【解析】【解答】解:A、把这些数从小到大排列为:5,5,6,6,6,7,7,则中位数是6,故本选项说法正确,不符合题意;
B、∵6出现了3次,出现的次数最多,∴众数是6,故本选项说法正确,不符合题意;
C、平均数是(5+5+6+6+6+7+7)÷7=6,故本选项说法正确,不符合题意;
D、方差= ×[2×(5 6)2+3×(6 6)2+2×(7 6)2]= ,故本选项说法错误,符合题意;
故答案为:D.
【分析】求中位数的方法是:把数据先按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,据此可对A,B作出判断;利用平均数公式求出这组数据的平均数,可对C作出判断;利用方差公式求出该组数据的方差,可对D作出判断.
8.【答案】C
【知识点】平均数及其计算;中位数;方差
【解析】【解答】解:A、由方差计算公式可知,总人数为6人,故我国一共派出了6名选手,∴A不符合题意;
B、由方差计算公式可知,平均数为38,故平均成绩为38分,∴B不符合题意;
C 、由方差计算公式无法判断出中位数的值,∴C符合题意;
D、由方差计算公式可知,总分=,∴D不符合题意.
故答案为:C.
【分析】利用方差的定义及计算方法和步骤可得平均数的大小,再逐项分析判断即可.
9.【答案】A
【知识点】二元一次方程组的应用-几何问题
【解析】【解答】解:∵∠BON+∠MOA+∠MON=180°,
∴x+y=90°,且由题可知,x-y=10°,
故答案为:A.
【分析】利用角的运算及图形可得∠BON+∠MOA+∠MON=180°,再结合 ∠BON=x°,∠MOA=y° 可得x+y=90°,再图形可得x-y=10°,从而可得方程组.
10.【答案】B
【知识点】待定系数法求一次函数解析式;一次函数的其他应用
【解析】【解答】解:由图可得:一次函数经过点和
∴设一次函数的解析式为:,把点和代入得:
解得:
∴
∴把代入得:.
故答案为:B.
【分析】结合函数图象中的数据,再利用待定系数法求出函数解析式,最后将x=0代入计算即可.
11.【答案】C
【知识点】一次函数与二元一次方程(组)的关系
【解析】【解答】解:∵一次函数y=k1x+b1与y=k2x+b2的图象的交点坐标为(2,1),∴关于x,y的方程组的解是.
故答案为:C.
【分析】先将求二元一次方程组的解的问题转换为两个一次函数的图象交点问题,再结合函数图象直接求出方程组的解即可.
12.【答案】A
【知识点】一次函数的图象
【解析】【解答】解:①当,、的图象都经过一、二、三象限;
②当,、的图象都经过二、三、四象限;
③当,的图象都经过一、三、四象限,的图象都经过一、二、四象限;
④当,的图象都经过一、二、四象限,的图象都经过一、三、四象限;
满足题意的只有A,
故答案为:A.
【分析】利用一次函数的图象、性质与系数的关系(①当k>0时,一次函数的图象呈上升趋势;②当k<0时,一次函数的图象呈下降趋势;③当b>0时,函数图象经过y轴的正半轴;④当b<0时,函数图象经过y轴的负半轴)分析求解即可.
13.【答案】C
【知识点】一次函数的性质
【解析】【解答】解:在一次函数y=2x+1中,
∵k=2>0,
∴y随x的增大而增大.
∵2< ,
∴.
∴m故答案为:C
【分析】根据k=2>0,可得y随x的增大而增大,再利用此性质结合可得答案。
14.【答案】B
【知识点】平行线的判定
【解析】【解答】解:①∵∠1=∠3,
∴AD∥BC;
②∵∠2+∠5=180°,∠5=∠AGC,
∴∠2+∠AGC=180°,
∴AB∥DC;
③∵∠4=∠B,
∴AB∥DC;
④∵∠D+∠BCD=180°,
∴AD∥BC.
综上,只有①④能判断AD∥BC.
故答案为:B.
【分析】利用同位角相等的两条直线平行、同位角相等的两条直线平行或同旁内角互补的两条直线平行的判定方法分析求解即可.
15.【答案】A
【知识点】一次函数与一元一次方程的关系
【解析】【解答】解:∵直线y=3x和直线y=ax+b交于点(1,3)
∴方程3x=ax+b的解为x=1.
故答案为:A.
【分析】先将求一元一次方程的解的问题转换为两个一次函数的图象交点问题(两个一次函数图象的交点横坐标即是方程的解),再结合函数图象直接求出方程的解即可.
16.【答案】B
【知识点】二元一次方程组的实际应用-方案选择题问题
【解析】【解答】解:设1支笔的价格为x元,1个本的价格为y元,
根据题意可得,,
解得:,
设小伟购买笔m支,本n个,
根据题意可得,,化简得,
当时,,
当时,,
当时,,
当时,,
∴小伟的购买方案共有4种,
故答案为:B.
【分析】设1支笔的价格为x元,1个本的价格为y元,根据“ 明明用元买了1支笔和4个本,亮亮用元买了2支笔和3个本 ”列出方程组求出笔和本的单价,再设小伟购买笔m支,本n个,根据“ 小伟购买上述价格的笔和本共用了元 ”列出二元一次方程,再求解即可.
17.【答案】
【知识点】二元一次方程的应用;坐标与图形性质
【解析】【解答】解:点A既是“健康点”又是“快乐点”,则A坐标应该满足和,
解
得:,
∴A的坐标为;
故答案为:.
【分析】利用“健康点”和“快乐点”的定义和点A既是“健康点”又是“快乐点”列出方程组,再求解即可.
18.【答案】
【知识点】待定系数法求一次函数解析式;坐标系中的两点距离公式
【解析】【解答】解:对于,
当时,,解得,即,
当时,,即,
由两点之间的距离公式得:,
以点A为圆心,AB长为半径画弧,交轴的负半轴于点C,
,
设点C的坐标为,
,
解得,
,
设直线BC的解析式为,
将点,代入得:,解得,
则直线BC的解析式为,
故答案为:.
【分析】先利用一次函数解析式求出点A、B的坐标,再利用勾股定理求出AB的长,再求出点C的坐标,最后利用待定系数法求出直线BC的解析式即可.
19.【答案】89.3
【知识点】加权平均数及其计算
【解析】【解答】小明的数学期末成绩是 =89.3(分),
故答案为:89.3.
【分析】利用加权平均数公式计算即可.
20.【答案】
【知识点】三角形内角和定理;同旁内角的概念
【解析】【解答】解:∵,
∴,
在中,,
∴;
故答案为:.
【分析】利用平行线的性质可得,再利用三角形的内角和及角的运算求出求出即可.
21.【答案】解:原式=3
=-1;
(2),
①×2-②得:5x=-5,
解得:x=-1,
把x=-1代入①得:y=1.
所以原方程组的解为.
【知识点】二次根式的混合运算;加减消元法解二元一次方程组
【解析】【分析】(1)利用二次根式的混合运算的计算方法及步骤(①有括号先算括号内;②再算二次根式的乘除;③最后计算二次根式的加减法)分析求解即可.
(2)利用加减消元法的计算方法及步骤分析求解即可.
22.【答案】(1)解:设捐款30元的有人,则可得:
,
解得.
则捐款人数共有(人).
答:他们一共调查了78人
(2)解:由图象可知:众数为25(元);
又捐款10元的人数为9人,15元的人数为12人,20元的人数为15人,25元的为24人,30元的为18人,
由于本组数据的个数为78,按大小顺序排列处于中间位置的两个数是第39个和40个,都是25(元),
故中位数为(元)
【知识点】条形统计图;中位数;众数
【解析】【分析】(1)设捐款30元的有人,根据“ 此次调查中捐款25元和30元的学生一共42人 ”列出方程,再求解即可;
(2)利用中位数的定义及计算方法(将一组数据按大小顺序排列后,位于中间位置的数值。如果数据量是奇数,则中位数是正中间的那个数;如果数据量是偶数,则中位数是中间两个数的平均值)和众数的定义及计算方法(众数是指在一组数据中出现次数最多的数值。众数有时不只一个,如果有两个或两个以上的数值出现次数相同且最多,则这些数值都是这组数据的众数)分析求解即可.
23.【答案】解:(1)小敏:小颖:.
(2)小敏:甲工程队绿化河岸的天数,乙工程队绿化河岸的天数.
小颖:甲工程队绿化河岸的长度,乙工程队绿化河岸的长度.
(3)选择方案一:解小敏的方程组.
原方程组可化为,
①,得,③
②③,得,
把代入①,得,
,.
答:甲、乙两工程队分别绿化河岸和.
选择方案二:解小颖的方程组.
原方程组可化为
①,得,③
②③,得,把代入①,得.
答:甲、乙两工程队分别绿化河岸和.
【知识点】二元一次方程组的实际应用-工程问题
【解析】【分析】(1)根据题干中的信息直接补全小敏和小颖的方程组即可;
(2)根据(1)的方程组分析求解即可;
(3)先任选一种方案,再利用二元一次方程组的计算方法分析求解即可.
24.【答案】(1)
(2)
(3)解:∵分别是和的角平分线,
∴,,
∴,
∴,即,
同理:,
∵四边形内角和等于360°,
∴,
由(1)知:,
∴,
∴,
【知识点】角的运算;三角形内角和定理;角平分线的性质
【解析】【解答】(1)解:∵,
∴,
∵的平分线交于点C,
∴,
∴,
故答案为:;
(2)解:在中,,
∵的平分线交于点C,
∴,
即,
∴;
故答案为:;
【分析】(1)先利用角平分线的定义及角的运算求出,再求出即可;
(2)先利用角平分线的定义及角的运算求出,再求出即可;
(3)先利用角平分线的定义及角的运算求出,即,,再利用四边形的内角和求出,再结合,最后求出即可.
25.【答案】(1),
(2)解:设甲地接种速度放缓后y与x的解析式为,
∵点在函数图象上,
∴,
解得:,
∴函数解析式为;
(3)解:由可得当时, ,
∴甲地未接种疫苗的人数万人;
【知识点】待定系数法求一次函数解析式;通过函数图象获取信息;一次函数的其他应用
【解析】【解答】解:∵乙地80天接种了40万人,
∴乙地每天接种的人数万人,
∵从开始到a天之间,两地接种速度相同,
∴此时甲地每天接种的人数0.5万人,
∵甲地a天接种了万人,
∴,
故答案为:,;
【分析】(1)根据函数图象中的数据列出算式分析求解即可;
(2)结合函数图象中的数据并利用待定系数法求出函数解析式即可;
(3)将x=80代入解析式求出y的值,再列出算式求出甲地未接种疫苗的人数即可.
一、相信你.你会选(1-10每小题3分,11-16每小题2分共42分)
1.下列各组数中都是无理数的为( )
A. B. C. D.
2.下列各式中,正确的是( )
A. B. C. D.
3.一组数据按从小到大排列为3,4,7,x,15,17,若这组数据的中位数为9,则x是( )
A.9 B.10 C.11 D.12
4.已知一个二元一次方程的一个解是,则这个方程可能是( )
A. B. C. D.
5.已知二元一次方程组 ,把②代入①,整理,得( )
A.x﹣2x+1=4 B.x﹣2x﹣1=4 C.x﹣6x﹣3=6 D.x﹣6x+3=4
6.以方程组的解为坐标的点,在平面直角坐标系中的位置是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.据统计,某班7个学习小组上周参加“青年大学习”的人数分别为:5,5,6,6,6,7,7,下列说法错误的是( )
A.该组数据的中位数是6 B.该组数据的众数是6
C.该组数据的平均数是6 D.该组数据的方差是6
8.在第60届国际数学奥林匹克比赛中,中国队荣获团体总分第一名.我国参赛选手比赛成绩的方差计算公式为:,下列说法错误的是( ).
A.我国一共派出了6名选手 B.我国参赛选手的平均成绩为38分
C.我国选手比赛成绩的中位数为38 D.我国选手比赛成绩的团体总分为228分
9.如图,直线AB,CD,相交于点O,∠MON=90°.∠BON比∠MOA多10°.求∠BON,∠MOA的度数若设∠BON=x°,∠MOA=y°.可列方程组为( )
A. B. C. D.
10.某公司市场营销部的个人收入(元)与其每月的销售量(万件)成一次函数关系,其图象如图所示,营销人员没有销售量时最低收入是( )
A.1000 B.2000 C.3000 D.4000
11.在平面直角坐标系内,一次函数y=k1x+b1与y=k2x+b2的图象如图所示,则关于x,y的方程组的解是( )
A. B. C. D.
12.已知一次函数和,函数和的图象可能是 ( )
A. B.
C. D.
13.已知点
,
在一次函数
的图像上,则m与n的大小关系是( )
A. B.m=n C.m<n D.无法确定
14.如图,点E在BC的延长线上,对于给出的四个条件:①∠1=∠3;②∠2+∠5=180°;③∠4=∠B;④∠D+∠BCD=180°.其中能判断AD∥BC的是( )
A.①② B.①④ C.①③ D.②④
15.如图,直线和直线交于点,根据图象分析,关于的方程的解为( )
A. B. C. D.
16.开学前明明、亮亮和小伟去购买学习用品,明明用元买了1支笔和4个本,亮亮用元买了2支笔和3个本,小伟购买上述价格的笔和本共用了元,则小伟的购买方案共有( )
A.5种 B.4种 C.3种 D.2种
二、填空题:(每小题3分,共12分)
17.在平面直角坐标系中,若点的坐标满足,则我们称点P为“健康点”;若点的坐标满足,则我们称点Q为“快乐点”,若点A既是“健康点”又是“快乐点”,则点A的坐标为 .
18.如图,在平面直角坐标系中,直线交轴于点A,交轴于点B,以点A为圆心,AB长为半径画弧,交轴的负半轴于点C,则直线BC的解析式为 .
19.某校规定学生的期末学科成绩由三部分组成,将课堂、作业和考试三项得分按1:3:6的权重确定每个人的期末成绩.小明同学本学期数学这三项得分分别是:课堂98分,作业95分,考试85分,那么小明的数学期末成绩是 分.
20.如图1,已知直线,且和分别相交于A,B两点,和分别交于C,D两点,点P在线段上若,则 .
三、简答题:(本题共46分)
21.计算下列各题:
(1);
(2).
22.在甘肃抗震救灾捐款活动中,某市振兴中学某班的学生对本校学生自愿捐款活动进行抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,图中从左到右各长方形的高度之比为,又知此次调查中捐款25元和30元的学生一共42人.
(1)他们一共调查了多少人?
(2)这组数据的众数,中位数各是多少?
23.列方程(组)解应用题:
汾河古称“汾”,又称汾水,是山西最大的河流,被山西人称为“母亲河”,对山西省的历史文化有着深远的影响.为打造“一川清水、两岸锦绣”的生态环境,现将一段长为的汾河两岸绿化任务交由甲、乙两个工程队先后接力完成.甲工程队每天绿化,乙工程队每天绿化,共用时天.
根据以上信息,小敏和小颖由自己的设想方案分别列出了尚不完整的方程组:
小敏:
小颖:
(1)请你在方框中补全小敏和小颖所列的方程组;
(2)根据小敏和小颖所列的方程组,分别指出未知数,表示的实际意义:
小敏:表示_____________,表示____________;
小颖:表示____________,表示______________;
(3)请你选择一种方案,求甲、乙两工程队分别绿化河岸多少米?
24.如图,点A、B分别在射线上运动(不与点O重合).
(1)如图1,若的平分线交于点C,则 ;
(2)如图2,若的平分线交于点C,则 ;
(3)如图2,若的外角的平分线交于点D,求与之间的数量关系,并求出的度数.
25.甲乙两地分别对本地各40万人接种某种疫苗,甲地在前期完成5万人接种后,甲、乙两地同时以相同速度接种,甲地经过a天后接种人数达到25万人,由于情况变化,接种速度放缓,结果100天完成接种任务,乙地80天完成接种任务,在某段时间内,甲、乙两地的接种人数y(万人)与各自接种时间x(天)之间的关系如图所示.
(1)乙地每天接种_________万人,
(2)当甲地接种速度放缓后,求y关于x的函数表达式;
(3)当乙地完成接种任务时,求甲地未接种疫苗的人数.
答案解析部分
1.【答案】C
【知识点】无理数的概念;求算术平方根
【解析】【解答】解:A、∵中的0.07,不是无理数,∴A错误;
B、∵中的不是无理数,∴B错误;
C、∵中的都是无理数,∴C正确;
D,∵中的不是无理数,∴D错误.
故答案为:C.
【分析】利用无理数的定义(无限不循环小数称为无理数)逐个分析判断求解即可.
2.【答案】D
【知识点】立方根及开立方;二次根式的性质与化简
【解析】【解答】解:A、原式 ,不符合题意;
B、原式 ,不符合题意;
C、原式 ,不符合题意;
D、原式 ,符合题意,
故答案为:D.
【分析】利用指数幂的运算性质即可得出答案。
3.【答案】C
【知识点】中位数
【解析】【解答】解:由题意得,(7+x)÷2=9,
解得:x=11.
故答案为:C.
【分析】根据中位数为中间两个数据的平均数可得(7+x)÷2=9,计算即可.
4.【答案】B
【知识点】二元一次方程的解
【解析】【解答】解:A、∵将代入,等式左右两边不相等,∴A是错误的;
B、∵将代入,等式左右两边相等,∴B是正确的;
C、∵将代入,等式左右两边不相等,∴C是错误的;
D、∵将代入,等式左右两边不相等,∴D错误的;
故答案为:B.
【分析】将分别代入各选项进行计算并判断即可.
5.【答案】D
【知识点】代入消元法解二元一次方程组
【解析】【解答】解: ,
把②代入①得:x﹣3(2x﹣1)=4,
整理,得:x﹣6x+3=4
故答案为:D.
【分析】利用代入消元法求解即可。
6.【答案】B
【知识点】点的坐标与象限的关系;加减消元法解二元一次方程组
【解析】【解答】解:
由,得:,
解得:.
将代入①,得:,
解得:,
∴原方程组的解为,
∴点在平面直角坐标系中的位置是第二象限.
故答案为:B.
【分析】先利用加减消元法的计算方法及步骤求出解集,再利用四个象限点坐标的符号特点(①第一象限(+,+);②第二象限(-,+);③第三象限(-,-);④第四象限(+,-))分析求解即可.
7.【答案】D
【知识点】平均数及其计算;中位数;方差;众数
【解析】【解答】解:A、把这些数从小到大排列为:5,5,6,6,6,7,7,则中位数是6,故本选项说法正确,不符合题意;
B、∵6出现了3次,出现的次数最多,∴众数是6,故本选项说法正确,不符合题意;
C、平均数是(5+5+6+6+6+7+7)÷7=6,故本选项说法正确,不符合题意;
D、方差= ×[2×(5 6)2+3×(6 6)2+2×(7 6)2]= ,故本选项说法错误,符合题意;
故答案为:D.
【分析】求中位数的方法是:把数据先按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,据此可对A,B作出判断;利用平均数公式求出这组数据的平均数,可对C作出判断;利用方差公式求出该组数据的方差,可对D作出判断.
8.【答案】C
【知识点】平均数及其计算;中位数;方差
【解析】【解答】解:A、由方差计算公式可知,总人数为6人,故我国一共派出了6名选手,∴A不符合题意;
B、由方差计算公式可知,平均数为38,故平均成绩为38分,∴B不符合题意;
C 、由方差计算公式无法判断出中位数的值,∴C符合题意;
D、由方差计算公式可知,总分=,∴D不符合题意.
故答案为:C.
【分析】利用方差的定义及计算方法和步骤可得平均数的大小,再逐项分析判断即可.
9.【答案】A
【知识点】二元一次方程组的应用-几何问题
【解析】【解答】解:∵∠BON+∠MOA+∠MON=180°,
∴x+y=90°,且由题可知,x-y=10°,
故答案为:A.
【分析】利用角的运算及图形可得∠BON+∠MOA+∠MON=180°,再结合 ∠BON=x°,∠MOA=y° 可得x+y=90°,再图形可得x-y=10°,从而可得方程组.
10.【答案】B
【知识点】待定系数法求一次函数解析式;一次函数的其他应用
【解析】【解答】解:由图可得:一次函数经过点和
∴设一次函数的解析式为:,把点和代入得:
解得:
∴
∴把代入得:.
故答案为:B.
【分析】结合函数图象中的数据,再利用待定系数法求出函数解析式,最后将x=0代入计算即可.
11.【答案】C
【知识点】一次函数与二元一次方程(组)的关系
【解析】【解答】解:∵一次函数y=k1x+b1与y=k2x+b2的图象的交点坐标为(2,1),∴关于x,y的方程组的解是.
故答案为:C.
【分析】先将求二元一次方程组的解的问题转换为两个一次函数的图象交点问题,再结合函数图象直接求出方程组的解即可.
12.【答案】A
【知识点】一次函数的图象
【解析】【解答】解:①当,、的图象都经过一、二、三象限;
②当,、的图象都经过二、三、四象限;
③当,的图象都经过一、三、四象限,的图象都经过一、二、四象限;
④当,的图象都经过一、二、四象限,的图象都经过一、三、四象限;
满足题意的只有A,
故答案为:A.
【分析】利用一次函数的图象、性质与系数的关系(①当k>0时,一次函数的图象呈上升趋势;②当k<0时,一次函数的图象呈下降趋势;③当b>0时,函数图象经过y轴的正半轴;④当b<0时,函数图象经过y轴的负半轴)分析求解即可.
13.【答案】C
【知识点】一次函数的性质
【解析】【解答】解:在一次函数y=2x+1中,
∵k=2>0,
∴y随x的增大而增大.
∵2< ,
∴.
∴m
【分析】根据k=2>0,可得y随x的增大而增大,再利用此性质结合可得答案。
14.【答案】B
【知识点】平行线的判定
【解析】【解答】解:①∵∠1=∠3,
∴AD∥BC;
②∵∠2+∠5=180°,∠5=∠AGC,
∴∠2+∠AGC=180°,
∴AB∥DC;
③∵∠4=∠B,
∴AB∥DC;
④∵∠D+∠BCD=180°,
∴AD∥BC.
综上,只有①④能判断AD∥BC.
故答案为:B.
【分析】利用同位角相等的两条直线平行、同位角相等的两条直线平行或同旁内角互补的两条直线平行的判定方法分析求解即可.
15.【答案】A
【知识点】一次函数与一元一次方程的关系
【解析】【解答】解:∵直线y=3x和直线y=ax+b交于点(1,3)
∴方程3x=ax+b的解为x=1.
故答案为:A.
【分析】先将求一元一次方程的解的问题转换为两个一次函数的图象交点问题(两个一次函数图象的交点横坐标即是方程的解),再结合函数图象直接求出方程的解即可.
16.【答案】B
【知识点】二元一次方程组的实际应用-方案选择题问题
【解析】【解答】解:设1支笔的价格为x元,1个本的价格为y元,
根据题意可得,,
解得:,
设小伟购买笔m支,本n个,
根据题意可得,,化简得,
当时,,
当时,,
当时,,
当时,,
∴小伟的购买方案共有4种,
故答案为:B.
【分析】设1支笔的价格为x元,1个本的价格为y元,根据“ 明明用元买了1支笔和4个本,亮亮用元买了2支笔和3个本 ”列出方程组求出笔和本的单价,再设小伟购买笔m支,本n个,根据“ 小伟购买上述价格的笔和本共用了元 ”列出二元一次方程,再求解即可.
17.【答案】
【知识点】二元一次方程的应用;坐标与图形性质
【解析】【解答】解:点A既是“健康点”又是“快乐点”,则A坐标应该满足和,
解
得:,
∴A的坐标为;
故答案为:.
【分析】利用“健康点”和“快乐点”的定义和点A既是“健康点”又是“快乐点”列出方程组,再求解即可.
18.【答案】
【知识点】待定系数法求一次函数解析式;坐标系中的两点距离公式
【解析】【解答】解:对于,
当时,,解得,即,
当时,,即,
由两点之间的距离公式得:,
以点A为圆心,AB长为半径画弧,交轴的负半轴于点C,
,
设点C的坐标为,
,
解得,
,
设直线BC的解析式为,
将点,代入得:,解得,
则直线BC的解析式为,
故答案为:.
【分析】先利用一次函数解析式求出点A、B的坐标,再利用勾股定理求出AB的长,再求出点C的坐标,最后利用待定系数法求出直线BC的解析式即可.
19.【答案】89.3
【知识点】加权平均数及其计算
【解析】【解答】小明的数学期末成绩是 =89.3(分),
故答案为:89.3.
【分析】利用加权平均数公式计算即可.
20.【答案】
【知识点】三角形内角和定理;同旁内角的概念
【解析】【解答】解:∵,
∴,
在中,,
∴;
故答案为:.
【分析】利用平行线的性质可得,再利用三角形的内角和及角的运算求出求出即可.
21.【答案】解:原式=3
=-1;
(2),
①×2-②得:5x=-5,
解得:x=-1,
把x=-1代入①得:y=1.
所以原方程组的解为.
【知识点】二次根式的混合运算;加减消元法解二元一次方程组
【解析】【分析】(1)利用二次根式的混合运算的计算方法及步骤(①有括号先算括号内;②再算二次根式的乘除;③最后计算二次根式的加减法)分析求解即可.
(2)利用加减消元法的计算方法及步骤分析求解即可.
22.【答案】(1)解:设捐款30元的有人,则可得:
,
解得.
则捐款人数共有(人).
答:他们一共调查了78人
(2)解:由图象可知:众数为25(元);
又捐款10元的人数为9人,15元的人数为12人,20元的人数为15人,25元的为24人,30元的为18人,
由于本组数据的个数为78,按大小顺序排列处于中间位置的两个数是第39个和40个,都是25(元),
故中位数为(元)
【知识点】条形统计图;中位数;众数
【解析】【分析】(1)设捐款30元的有人,根据“ 此次调查中捐款25元和30元的学生一共42人 ”列出方程,再求解即可;
(2)利用中位数的定义及计算方法(将一组数据按大小顺序排列后,位于中间位置的数值。如果数据量是奇数,则中位数是正中间的那个数;如果数据量是偶数,则中位数是中间两个数的平均值)和众数的定义及计算方法(众数是指在一组数据中出现次数最多的数值。众数有时不只一个,如果有两个或两个以上的数值出现次数相同且最多,则这些数值都是这组数据的众数)分析求解即可.
23.【答案】解:(1)小敏:小颖:.
(2)小敏:甲工程队绿化河岸的天数,乙工程队绿化河岸的天数.
小颖:甲工程队绿化河岸的长度,乙工程队绿化河岸的长度.
(3)选择方案一:解小敏的方程组.
原方程组可化为,
①,得,③
②③,得,
把代入①,得,
,.
答:甲、乙两工程队分别绿化河岸和.
选择方案二:解小颖的方程组.
原方程组可化为
①,得,③
②③,得,把代入①,得.
答:甲、乙两工程队分别绿化河岸和.
【知识点】二元一次方程组的实际应用-工程问题
【解析】【分析】(1)根据题干中的信息直接补全小敏和小颖的方程组即可;
(2)根据(1)的方程组分析求解即可;
(3)先任选一种方案,再利用二元一次方程组的计算方法分析求解即可.
24.【答案】(1)
(2)
(3)解:∵分别是和的角平分线,
∴,,
∴,
∴,即,
同理:,
∵四边形内角和等于360°,
∴,
由(1)知:,
∴,
∴,
【知识点】角的运算;三角形内角和定理;角平分线的性质
【解析】【解答】(1)解:∵,
∴,
∵的平分线交于点C,
∴,
∴,
故答案为:;
(2)解:在中,,
∵的平分线交于点C,
∴,
即,
∴;
故答案为:;
【分析】(1)先利用角平分线的定义及角的运算求出,再求出即可;
(2)先利用角平分线的定义及角的运算求出,再求出即可;
(3)先利用角平分线的定义及角的运算求出,即,,再利用四边形的内角和求出,再结合,最后求出即可.
25.【答案】(1),
(2)解:设甲地接种速度放缓后y与x的解析式为,
∵点在函数图象上,
∴,
解得:,
∴函数解析式为;
(3)解:由可得当时, ,
∴甲地未接种疫苗的人数万人;
【知识点】待定系数法求一次函数解析式;通过函数图象获取信息;一次函数的其他应用
【解析】【解答】解:∵乙地80天接种了40万人,
∴乙地每天接种的人数万人,
∵从开始到a天之间,两地接种速度相同,
∴此时甲地每天接种的人数0.5万人,
∵甲地a天接种了万人,
∴,
故答案为:,;
【分析】(1)根据函数图象中的数据列出算式分析求解即可;
(2)结合函数图象中的数据并利用待定系数法求出函数解析式即可;
(3)将x=80代入解析式求出y的值,再列出算式求出甲地未接种疫苗的人数即可.
同课章节目录
