人教版数学九年级上册 第二十四章 圆 单元练习(含答案)
文档属性
| 名称 | 人教版数学九年级上册 第二十四章 圆 单元练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 516.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-21 00:00:00 | ||
图片预览



文档简介
人教版数学九上 第二十四章 圆 单元练习
一、单选题
1.已如的直径为,点到直线的距离为,则与的位置关系是( )
A.相离 B.相切 C.相交 D.相切或相交
2.用反证法证明:a,b至少有一个为0,应该假设( )
A.a,b没有一个为0 B.a,b只有一个为0
C.a,b至多一个为0 D.a,b两个都为0
3.如图,⊙O的弦AB=8,P是劣弧AB中点,连接OP交AB于C,且PC=2,则⊙O的半径为( )
A.8 B.4 C.5 D.10
4.已知过正方形顶点,,且与相切,若正方形边长为,则圆的半径为( )
A. B. C. D.
5.⊙O的直径为8,圆心O到直线a的距离为4,则直线a与⊙O的位置关系是( )
A.相离 B.相切 C.相交 D.不能确定
6.如图,切于点A,连接,作弦于点C,,则的度数为( )
A.35 B.40 C.50 D.55
7.如图,是的直径,与相切于点A,,的延长线交于点P,则的度数是( )
A. B. C. D.
8.如图,点A,B,C为⊙O上的三点,∠AOB=∠BOC,∠ACB=10°,则∠AOC的度数为( )
A.90° B.80° C.70° D.60°
9.如图,某数学兴趣小组将边长为 5 的正方形铁丝框ABCD变形为以A为圆心,AB 为半径 的扇形(忽略铁丝的粗细),则所得的扇形 ABD 的面积为( )
A. B. C.25 D.20
二、填空题
10.已知圆锥的母线长为4,其侧面积为,则它的底面圆的半径等于 .
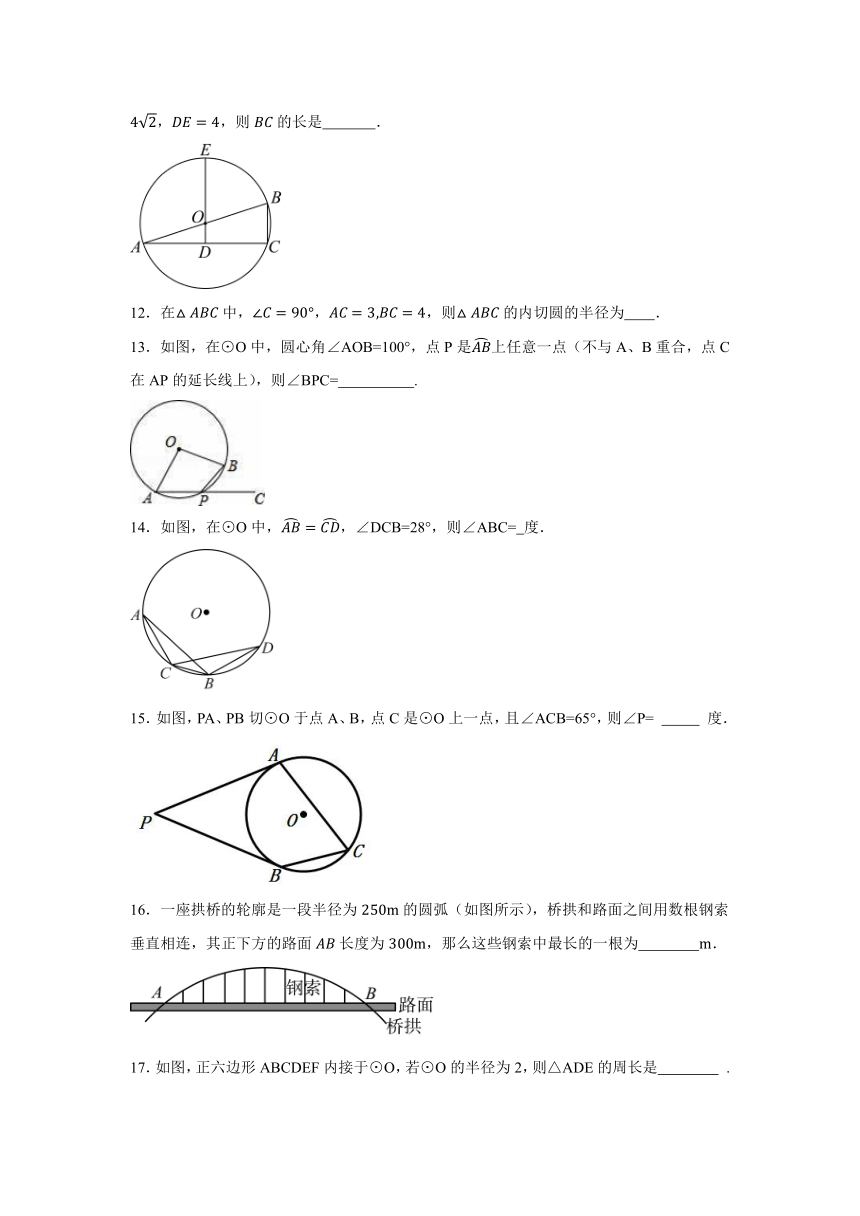
11.如图,是的直径,垂直于弦于点,的延长线交于点.若,,则的长是 .
12.在中,,,则的内切圆的半径为 .
13.如图,在⊙O中,圆心角∠AOB=100°,点P是上任意一点(不与A、B重合,点C在AP的延长线上),则∠BPC= .
14.如图,在⊙O中,,∠DCB=28°,则∠ABC= 度.
15.如图,PA、PB切⊙O于点A、B,点C是⊙O上一点,且∠ACB=65°,则∠P= 度.
16.一座拱桥的轮廓是一段半径为的圆弧(如图所示),桥拱和路面之间用数根钢索垂直相连,其正下方的路面长度为,那么这些钢索中最长的一根为 .
17.如图,正六边形ABCDEF内接于⊙O,若⊙O的半径为2,则△ADE的周长是 .
三、解答题
18.一根横截面为圆形的下水管道的直径为1米,管内有少量的污水(如图),此时的水面宽AB为0.6米.求此时的水深(即阴影部分的弓形高).
19.如图,⊙O中直径AB⊥弦CD于E,点F是的中点,CF交AB于I,连接BD、AC、AD.
(1)求证:BI=BD;
(2)若OI=1,OE=2,求⊙O的半径.
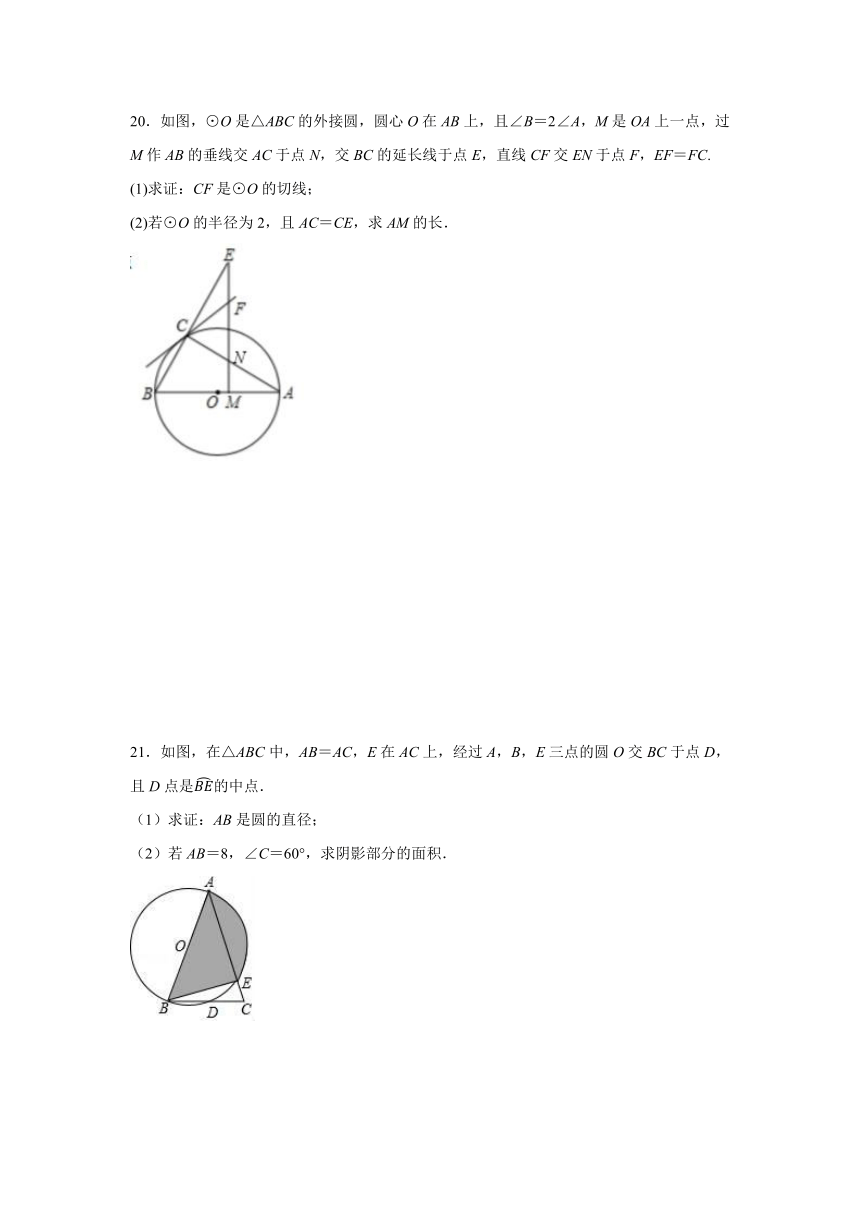
20.如图,⊙O是△ABC的外接圆,圆心O在AB上,且∠B=2∠A,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,EF=FC.
(1)求证:CF是⊙O的切线;
(2)若⊙O的半径为2,且AC=CE,求AM的长.
21.如图,在△ABC中,AB=AC,E在AC上,经过A,B,E三点的圆O交BC于点D,且D点是的中点.
(1)求证:AB是圆的直径;
(2)若AB=8,∠C=60°,求阴影部分的面积.
22.请仅用无刻度的直尺作图.
(1)如图1,是的内接三角形,点在上一点,且.画出中的平分线;
(2)如图2,是的内接三角形,是的中点.画出的的平分线;
(3)如图3,是的内接三角形,点在上一点,且,画出的外角的角平分线.
23.已知经过四边形的B、D两点,并与四条边分别交于点,且.
(1)如图①,连接,若是的直径,求证:;
(2)如图②,若的度数为,请直接写出和β之间的数量关系.
24.在平面直角坐标系中,定义点P(x,y)的变换点为P′(x+y,x﹣y).
(1)如图1,如果⊙O的半径为2,
①判断M(2,0),N(﹣2,1)两个点的变换点M′、N′与⊙O的位置关系;
②若点P在直线y=x-2上,点P的变换点P′不在⊙O外,结合图形求点P横坐标x的取值范围.
(2)如图2,如果⊙O的半径为1,且P的变换点P′在直线y=﹣2x+5上,求点P与⊙O上任意一点距离的最小值.
参考答案:
1.A
2.A
3.C
4.B
5.B
6.C
7.C
8.B
9.C
10.1.5
11.2
12.1
13.50°.
14.28
15.50
16.
17.6+
18.此时的水深为0.1米
19.(1)证明:如图,连接DI,
∵AB为⊙O的直径,且AB⊥CD,
∴,
∴∠CAB=∠BAD,∠BAD=∠BDC,
∵点F是的中点,
∴∠ACF=∠DCF,
∴I是△ADC的内心,
∴∠ADI=∠CDI,
∵∠BID=∠BAD+∠ADI,∠BDI=∠BDC+∠CDI,
∴∠BID=∠BDI,
∴BI=BD;
(2)连接OD,
设⊙O的半径为r,
∵OI=1,OE=2,
∴BE=r﹣2,BD=BI=r+1,
由勾股定理得:DE2=r2﹣22=(r+1)2﹣(r﹣2)2,
r2﹣6r﹣1=0,
r1=3+,r2=3-(舍),
答:⊙O的半径是3+.
20.(1)证明:如图,连接OC.
∵⊙O是△ABC的外接圆,圆心O在AB上,
∴AB是⊙O的直径,
∴∠ACB=90°.
又∵∠B=2∠A,
∴∠B=60°,∠A=30°.
∵EM⊥AB,∴∠EMB=90°.
在Rt△EMB中,∠B=60°,
∴∠E=30°.
又∵EF=FC,
∴∠ECF=∠E=30°.
又∵∠ECA=90°,
∴∠FCA=60°.
∵OA=OC,
∴∠OCA=∠A=30°,
∴∠FCO=∠FCA+∠ACO=90°,
∴OC⊥CF,
∴FC是⊙O的切线;
(2)在Rt△ABC中,∵∠ACB=90°,∠A=30°,AB=4,
∴BC=AB=2,AC==BC=
∵AC=CE,
∴CE=2,
∴BE=BC+CE=2+
在Rt△BEM中,∠BME=90°,∠E=30°,
∴BM=BE=1+,
∴AM=AB-BM=4-1-=3-.
21.解:(1)连接AD,
∵D点是的中点,
∴∠BAD=∠CAD,
又∵AB=AC,
∴AD⊥BD,
∴∠ADB=90°,
∴AB是⊙O直径;
(2)连接OE,
∵∠C=60°,AB=AC,
∴∠BAC=60°,
∴∠AOE=60°,
∴∠BOE=120°,
∴∠OBE=30°,
∵AB=8,
∴OB=4,
∴S阴影=S扇形AOE+S△BOE==π+4.
22.(1)解:连接,则射线即为所求,
,
,
是的角平分线;
(2)解:连接并延长与圆交于点,连接,则射线即为所求,
是的中点,
,
,
,
是的平分线;
(3)解:如图3,延长交于G,则射线为所求.
理由:连接,
∵,经过圆心,
∴垂直平分,
∴,
∴,
根据圆内接四边形的性质得:,
∵,
∴,
∵,
∴,即平分.
23.(1)连接,如图①:
∵是的直径,
∴,
∵,
∴,
∵,,
∴.
(2)结论:;理由如下:
如图②中,连接,
∵,
∴,
∵,
∴,
∵,
∴,
∴.
24.(1)①M(2,0)的变换点M′的坐标为(2,2),则OM′==2,所以点M(2,0)的变换点在⊙O上;
N(-2,1)的变换点N′的坐标为(-1,-3),则ON′==>2,所以点N(-2,-1)的变换点在⊙O外;
②设P点坐标为(x,x-2),则P点的变换点为P′的坐标为(2x-2,2),则OP′=,
∵点P′不在⊙O外,
∴≤2,
∴(2x-2)2≤4,即(x-1)2≤1,
∴-1≤x-1≤1,解得0≤x≤2,
即点P横坐标的取值范围为0≤x≤2;
(2)设点P′的坐标为(x,-2x+5),P(m,n),
根据题意得m+n=x,m-n=-2x+5,
∴3m+n=5,
即n=-3m+5,
∴P点坐标为(m,-3m+5),
∴点P在直线y=-3x+5上,
设直线y=-3x+5与x轴相交于点A,与y轴相交于点B,过O点作OH⊥AB于H,交⊙O于C,如图,
则A(,0),B(0,5),
∴AB==,
∵OH AB=OA OB,
∴OH==,
∴CH=-1,
即点P与⊙O上任意一点距离的最小值为-1.
一、单选题
1.已如的直径为,点到直线的距离为,则与的位置关系是( )
A.相离 B.相切 C.相交 D.相切或相交
2.用反证法证明:a,b至少有一个为0,应该假设( )
A.a,b没有一个为0 B.a,b只有一个为0
C.a,b至多一个为0 D.a,b两个都为0
3.如图,⊙O的弦AB=8,P是劣弧AB中点,连接OP交AB于C,且PC=2,则⊙O的半径为( )
A.8 B.4 C.5 D.10
4.已知过正方形顶点,,且与相切,若正方形边长为,则圆的半径为( )
A. B. C. D.
5.⊙O的直径为8,圆心O到直线a的距离为4,则直线a与⊙O的位置关系是( )
A.相离 B.相切 C.相交 D.不能确定
6.如图,切于点A,连接,作弦于点C,,则的度数为( )
A.35 B.40 C.50 D.55
7.如图,是的直径,与相切于点A,,的延长线交于点P,则的度数是( )
A. B. C. D.
8.如图,点A,B,C为⊙O上的三点,∠AOB=∠BOC,∠ACB=10°,则∠AOC的度数为( )
A.90° B.80° C.70° D.60°
9.如图,某数学兴趣小组将边长为 5 的正方形铁丝框ABCD变形为以A为圆心,AB 为半径 的扇形(忽略铁丝的粗细),则所得的扇形 ABD 的面积为( )
A. B. C.25 D.20
二、填空题
10.已知圆锥的母线长为4,其侧面积为,则它的底面圆的半径等于 .
11.如图,是的直径,垂直于弦于点,的延长线交于点.若,,则的长是 .
12.在中,,,则的内切圆的半径为 .
13.如图,在⊙O中,圆心角∠AOB=100°,点P是上任意一点(不与A、B重合,点C在AP的延长线上),则∠BPC= .
14.如图,在⊙O中,,∠DCB=28°,则∠ABC= 度.
15.如图,PA、PB切⊙O于点A、B,点C是⊙O上一点,且∠ACB=65°,则∠P= 度.
16.一座拱桥的轮廓是一段半径为的圆弧(如图所示),桥拱和路面之间用数根钢索垂直相连,其正下方的路面长度为,那么这些钢索中最长的一根为 .
17.如图,正六边形ABCDEF内接于⊙O,若⊙O的半径为2,则△ADE的周长是 .
三、解答题
18.一根横截面为圆形的下水管道的直径为1米,管内有少量的污水(如图),此时的水面宽AB为0.6米.求此时的水深(即阴影部分的弓形高).
19.如图,⊙O中直径AB⊥弦CD于E,点F是的中点,CF交AB于I,连接BD、AC、AD.
(1)求证:BI=BD;
(2)若OI=1,OE=2,求⊙O的半径.
20.如图,⊙O是△ABC的外接圆,圆心O在AB上,且∠B=2∠A,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,EF=FC.
(1)求证:CF是⊙O的切线;
(2)若⊙O的半径为2,且AC=CE,求AM的长.
21.如图,在△ABC中,AB=AC,E在AC上,经过A,B,E三点的圆O交BC于点D,且D点是的中点.
(1)求证:AB是圆的直径;
(2)若AB=8,∠C=60°,求阴影部分的面积.
22.请仅用无刻度的直尺作图.
(1)如图1,是的内接三角形,点在上一点,且.画出中的平分线;
(2)如图2,是的内接三角形,是的中点.画出的的平分线;
(3)如图3,是的内接三角形,点在上一点,且,画出的外角的角平分线.
23.已知经过四边形的B、D两点,并与四条边分别交于点,且.
(1)如图①,连接,若是的直径,求证:;
(2)如图②,若的度数为,请直接写出和β之间的数量关系.
24.在平面直角坐标系中,定义点P(x,y)的变换点为P′(x+y,x﹣y).
(1)如图1,如果⊙O的半径为2,
①判断M(2,0),N(﹣2,1)两个点的变换点M′、N′与⊙O的位置关系;
②若点P在直线y=x-2上,点P的变换点P′不在⊙O外,结合图形求点P横坐标x的取值范围.
(2)如图2,如果⊙O的半径为1,且P的变换点P′在直线y=﹣2x+5上,求点P与⊙O上任意一点距离的最小值.
参考答案:
1.A
2.A
3.C
4.B
5.B
6.C
7.C
8.B
9.C
10.1.5
11.2
12.1
13.50°.
14.28
15.50
16.
17.6+
18.此时的水深为0.1米
19.(1)证明:如图,连接DI,
∵AB为⊙O的直径,且AB⊥CD,
∴,
∴∠CAB=∠BAD,∠BAD=∠BDC,
∵点F是的中点,
∴∠ACF=∠DCF,
∴I是△ADC的内心,
∴∠ADI=∠CDI,
∵∠BID=∠BAD+∠ADI,∠BDI=∠BDC+∠CDI,
∴∠BID=∠BDI,
∴BI=BD;
(2)连接OD,
设⊙O的半径为r,
∵OI=1,OE=2,
∴BE=r﹣2,BD=BI=r+1,
由勾股定理得:DE2=r2﹣22=(r+1)2﹣(r﹣2)2,
r2﹣6r﹣1=0,
r1=3+,r2=3-(舍),
答:⊙O的半径是3+.
20.(1)证明:如图,连接OC.
∵⊙O是△ABC的外接圆,圆心O在AB上,
∴AB是⊙O的直径,
∴∠ACB=90°.
又∵∠B=2∠A,
∴∠B=60°,∠A=30°.
∵EM⊥AB,∴∠EMB=90°.
在Rt△EMB中,∠B=60°,
∴∠E=30°.
又∵EF=FC,
∴∠ECF=∠E=30°.
又∵∠ECA=90°,
∴∠FCA=60°.
∵OA=OC,
∴∠OCA=∠A=30°,
∴∠FCO=∠FCA+∠ACO=90°,
∴OC⊥CF,
∴FC是⊙O的切线;
(2)在Rt△ABC中,∵∠ACB=90°,∠A=30°,AB=4,
∴BC=AB=2,AC==BC=
∵AC=CE,
∴CE=2,
∴BE=BC+CE=2+
在Rt△BEM中,∠BME=90°,∠E=30°,
∴BM=BE=1+,
∴AM=AB-BM=4-1-=3-.
21.解:(1)连接AD,
∵D点是的中点,
∴∠BAD=∠CAD,
又∵AB=AC,
∴AD⊥BD,
∴∠ADB=90°,
∴AB是⊙O直径;
(2)连接OE,
∵∠C=60°,AB=AC,
∴∠BAC=60°,
∴∠AOE=60°,
∴∠BOE=120°,
∴∠OBE=30°,
∵AB=8,
∴OB=4,
∴S阴影=S扇形AOE+S△BOE==π+4.
22.(1)解:连接,则射线即为所求,
,
,
是的角平分线;
(2)解:连接并延长与圆交于点,连接,则射线即为所求,
是的中点,
,
,
,
是的平分线;
(3)解:如图3,延长交于G,则射线为所求.
理由:连接,
∵,经过圆心,
∴垂直平分,
∴,
∴,
根据圆内接四边形的性质得:,
∵,
∴,
∵,
∴,即平分.
23.(1)连接,如图①:
∵是的直径,
∴,
∵,
∴,
∵,,
∴.
(2)结论:;理由如下:
如图②中,连接,
∵,
∴,
∵,
∴,
∵,
∴,
∴.
24.(1)①M(2,0)的变换点M′的坐标为(2,2),则OM′==2,所以点M(2,0)的变换点在⊙O上;
N(-2,1)的变换点N′的坐标为(-1,-3),则ON′==>2,所以点N(-2,-1)的变换点在⊙O外;
②设P点坐标为(x,x-2),则P点的变换点为P′的坐标为(2x-2,2),则OP′=,
∵点P′不在⊙O外,
∴≤2,
∴(2x-2)2≤4,即(x-1)2≤1,
∴-1≤x-1≤1,解得0≤x≤2,
即点P横坐标的取值范围为0≤x≤2;
(2)设点P′的坐标为(x,-2x+5),P(m,n),
根据题意得m+n=x,m-n=-2x+5,
∴3m+n=5,
即n=-3m+5,
∴P点坐标为(m,-3m+5),
∴点P在直线y=-3x+5上,
设直线y=-3x+5与x轴相交于点A,与y轴相交于点B,过O点作OH⊥AB于H,交⊙O于C,如图,
则A(,0),B(0,5),
∴AB==,
∵OH AB=OA OB,
∴OH==,
∴CH=-1,
即点P与⊙O上任意一点距离的最小值为-1.
同课章节目录
