2024-2025学年华东师大版数学九年级上 册 23.3 相似三角形 同步练习(含答案)
文档属性
| 名称 | 2024-2025学年华东师大版数学九年级上 册 23.3 相似三角形 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 315.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-21 21:16:42 | ||
图片预览




文档简介
2024-2025学年华东师大版数学九上 23.3相似三角形 同步练习
一、单选题
1.如图,在中,为上一点,下列四个条件中:①;②;③﹔④能满足与相似的条件是( )
A.①②③ B.①②④ C.①③④ D.②③④
2.如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC,若=,则的值为 ( )
A.1:2 B.2:1 C.1:3 D.3:1
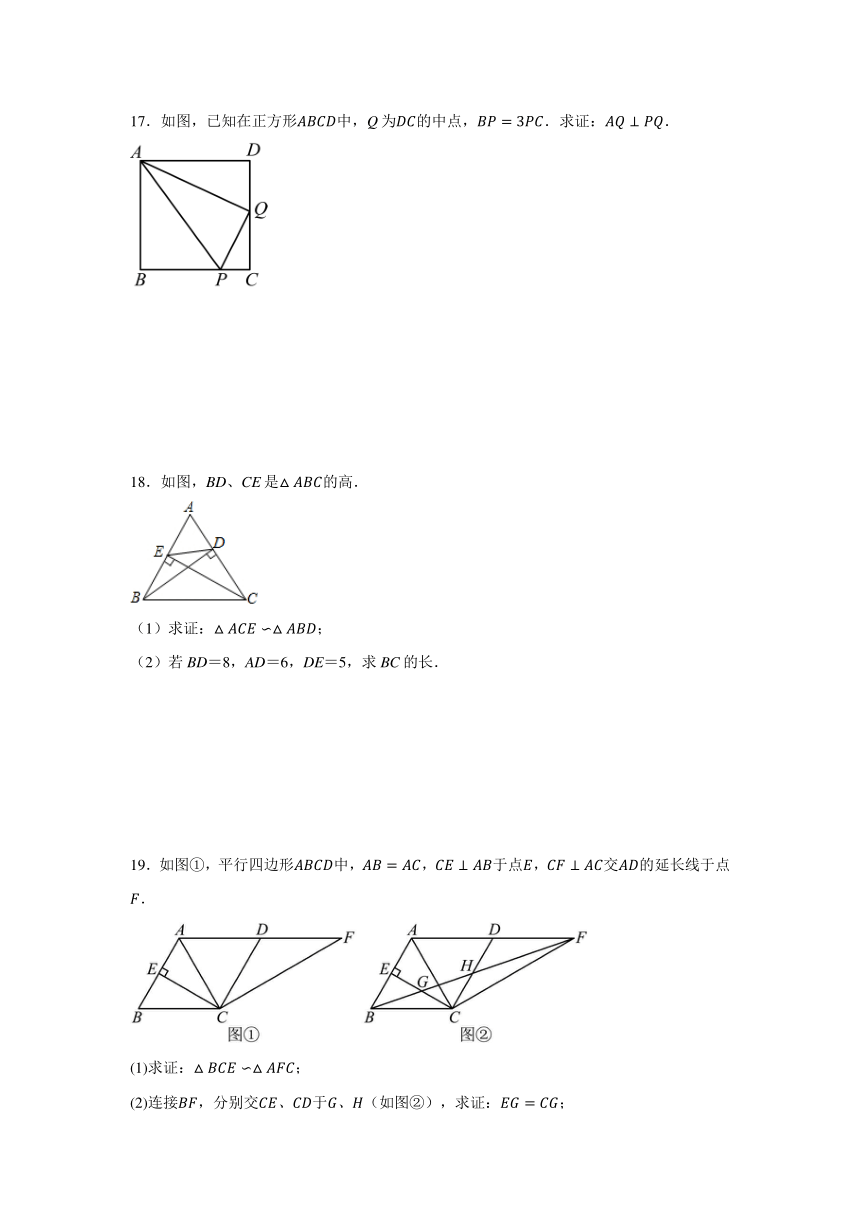
3.如图,中,,点D,E分别在上,,则( )
A. B. C.3 D.2
4.在正方形网格中,每个小正方形的顶点称为格点,如图,点,,,均在格点上,连接,相交于点,若小正方形的边长为1,则的长为( )
A. B. C. D.
5.已知△ABC和△ADC均为直角三角形,点B、D位于AC的两侧,∠ACB=∠ACD=90°,BC=a,AC=b,AB=c,要使△ADC和△ABC相似,CD可以等于( ).
A. B. C. D.
6.如图,在平行四边形中,的平分线交于点,交于点,交的延长线于点,若,则的值为( ).
A. B. C. D.
7.如图,在中,点分别在边上,且为边延长线上一点,连接,则图中与相似的三角形有( )个
A. B. C. D.
8.如图,在平面直角坐标系中,点A在函数 的图像上,点B在函数的图像上,若AO=2BO,∠AOB=90°,则k的值为( )
A.0.5 B.1 C.1.5 D.2
二、填空题
9.若与相似,已知,,,则 .
10.如图,在正方形网格上有6个三角形:①△ABC,②△CDB,③△DEB,④△FBG,⑤△HGF,⑥△EKF.在②~⑥中,与①相似的三角形的个数是 .
11.如图,的顶点在y轴上,两点都在x轴上,将边向右平移,平移后点的对应点为D,点的对应点为,线段交AC于点,若,则点的坐标为 .
12.如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线MN截△ABC交AC于点N,使截得的△CMN与△ABC相似.已知AB=6,AC=8,CM=4,则CN= .
13.如图,在△ABC中,∠BAC=90°,AB=AC=,点D、E分别在BC、AC上(点D不与点B、C重合),且∠ADE=45°,若△ADE是等腰三角形,则CE= .
14.如图,在中,,正方形的顶点D、G分别在、边上,在上,若,则正方形的边长为 .
15.如图,△ABC中,BC=1.若AD1=AB,且D1E1∥BC,则D1E1=;照这样继续下去,D1D2=D1B,且D2E2∥BC;D2D3=D2B,且D3E3∥BC;…;Dn-1Dn=n-1B,且DnEn∥BC,则DnEn= (用含n的式子表示).
三、解答题
16.如图,在中,的平分线交边于点,已知.
(1)求证:;
(2)若,求的度数.
17.如图,已知在正方形中,Q为的中点,.求证:.
18.如图,BD、CE是的高.
(1)求证:;
(2)若BD=8,AD=6,DE=5,求BC的长.
19.如图①,平行四边形中,,于点,交的延长线于点.
(1)求证:;
(2)连接,分别交于(如图②),求证:;
(3)在图②中,若,求.
20.如图,方格纸中每个小正方形的边长为1,△ABC和△DEF的顶点都在方格纸的格点上.
(1) 判断△ABC和△DEF是否相似,并说明理由;
(2) P1,P2,P3,P4,P5,D,F是△DEF边上的7个格点,请在这7个格点中选取3个点作为三角形的顶点,使构成的三角形与△ABC相似(要求写出2个符合条件的三角形,并在图中连接相应线段,不必说明理由).
参考答案:
1.C
2.C
3.A
4.C
5.B
6.B
7.D
8.D
9.
10.3
11.
12.5或
13.2﹣或.
14.
15.1-
16.(1)解:证明:∵平分,
∴,
∵,
∴,
∵,
∴,
∴,
∴即;
(2)由(1)得,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴.
17.证明:∵四边形是正方形,
∴.
∵Q为的中点,
∴.
∵,
∴,
∴,
∴.
又∵,
∴,
∴.
∵,
∴,
∴,
∴,
∴.
18.解:(1)证明:、是的高,
,
,
;
(2)在中,,,
根据勾股定理,得
,
,
,
,
,
,
,
.
19.(1)证明:,,
,
四边形是平行四边形,
,
,
,
,
,
;
(2)证明:,
,
四边形是平行四边形,
,,
,,
,,
,
,
,
,
,,
,
;
(3)解:,
是等边三角形,
,
,
由(2)可得:,
,
,,
,
,
,
,
,
,
,
,
.
20.解:(1) △ABC和△DEF相似.
根据勾股定理,得 ,,BC=5;
,,.
∵ ,
∴ △ABC∽△DEF.
(2) 答案不唯一,下面6个三角形中的任意2个均可.
△P2P5D,△P4P5F,△P2P4D,
△P4P5D,△P2P4P5,△P1FD.
一、单选题
1.如图,在中,为上一点,下列四个条件中:①;②;③﹔④能满足与相似的条件是( )
A.①②③ B.①②④ C.①③④ D.②③④
2.如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC,若=,则的值为 ( )
A.1:2 B.2:1 C.1:3 D.3:1
3.如图,中,,点D,E分别在上,,则( )
A. B. C.3 D.2
4.在正方形网格中,每个小正方形的顶点称为格点,如图,点,,,均在格点上,连接,相交于点,若小正方形的边长为1,则的长为( )
A. B. C. D.
5.已知△ABC和△ADC均为直角三角形,点B、D位于AC的两侧,∠ACB=∠ACD=90°,BC=a,AC=b,AB=c,要使△ADC和△ABC相似,CD可以等于( ).
A. B. C. D.
6.如图,在平行四边形中,的平分线交于点,交于点,交的延长线于点,若,则的值为( ).
A. B. C. D.
7.如图,在中,点分别在边上,且为边延长线上一点,连接,则图中与相似的三角形有( )个
A. B. C. D.
8.如图,在平面直角坐标系中,点A在函数 的图像上,点B在函数的图像上,若AO=2BO,∠AOB=90°,则k的值为( )
A.0.5 B.1 C.1.5 D.2
二、填空题
9.若与相似,已知,,,则 .
10.如图,在正方形网格上有6个三角形:①△ABC,②△CDB,③△DEB,④△FBG,⑤△HGF,⑥△EKF.在②~⑥中,与①相似的三角形的个数是 .
11.如图,的顶点在y轴上,两点都在x轴上,将边向右平移,平移后点的对应点为D,点的对应点为,线段交AC于点,若,则点的坐标为 .
12.如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线MN截△ABC交AC于点N,使截得的△CMN与△ABC相似.已知AB=6,AC=8,CM=4,则CN= .
13.如图,在△ABC中,∠BAC=90°,AB=AC=,点D、E分别在BC、AC上(点D不与点B、C重合),且∠ADE=45°,若△ADE是等腰三角形,则CE= .
14.如图,在中,,正方形的顶点D、G分别在、边上,在上,若,则正方形的边长为 .
15.如图,△ABC中,BC=1.若AD1=AB,且D1E1∥BC,则D1E1=;照这样继续下去,D1D2=D1B,且D2E2∥BC;D2D3=D2B,且D3E3∥BC;…;Dn-1Dn=n-1B,且DnEn∥BC,则DnEn= (用含n的式子表示).
三、解答题
16.如图,在中,的平分线交边于点,已知.
(1)求证:;
(2)若,求的度数.
17.如图,已知在正方形中,Q为的中点,.求证:.
18.如图,BD、CE是的高.
(1)求证:;
(2)若BD=8,AD=6,DE=5,求BC的长.
19.如图①,平行四边形中,,于点,交的延长线于点.
(1)求证:;
(2)连接,分别交于(如图②),求证:;
(3)在图②中,若,求.
20.如图,方格纸中每个小正方形的边长为1,△ABC和△DEF的顶点都在方格纸的格点上.
(1) 判断△ABC和△DEF是否相似,并说明理由;
(2) P1,P2,P3,P4,P5,D,F是△DEF边上的7个格点,请在这7个格点中选取3个点作为三角形的顶点,使构成的三角形与△ABC相似(要求写出2个符合条件的三角形,并在图中连接相应线段,不必说明理由).
参考答案:
1.C
2.C
3.A
4.C
5.B
6.B
7.D
8.D
9.
10.3
11.
12.5或
13.2﹣或.
14.
15.1-
16.(1)解:证明:∵平分,
∴,
∵,
∴,
∵,
∴,
∴,
∴即;
(2)由(1)得,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∴.
17.证明:∵四边形是正方形,
∴.
∵Q为的中点,
∴.
∵,
∴,
∴,
∴.
又∵,
∴,
∴.
∵,
∴,
∴,
∴,
∴.
18.解:(1)证明:、是的高,
,
,
;
(2)在中,,,
根据勾股定理,得
,
,
,
,
,
,
,
.
19.(1)证明:,,
,
四边形是平行四边形,
,
,
,
,
,
;
(2)证明:,
,
四边形是平行四边形,
,,
,,
,,
,
,
,
,
,,
,
;
(3)解:,
是等边三角形,
,
,
由(2)可得:,
,
,,
,
,
,
,
,
,
,
,
.
20.解:(1) △ABC和△DEF相似.
根据勾股定理,得 ,,BC=5;
,,.
∵ ,
∴ △ABC∽△DEF.
(2) 答案不唯一,下面6个三角形中的任意2个均可.
△P2P5D,△P4P5F,△P2P4D,
△P4P5D,△P2P4P5,△P1FD.
