2024-2025学年华东师大版数学九年级上册 23.3.4 相似三角形的应用 同步练习(含答案)
文档属性
| 名称 | 2024-2025学年华东师大版数学九年级上册 23.3.4 相似三角形的应用 同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 491.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-21 21:18:49 | ||
图片预览


文档简介
2024-2025学年华东师大版数学九上 23.3.4相似三角形的应用 同步练习
一、单选题
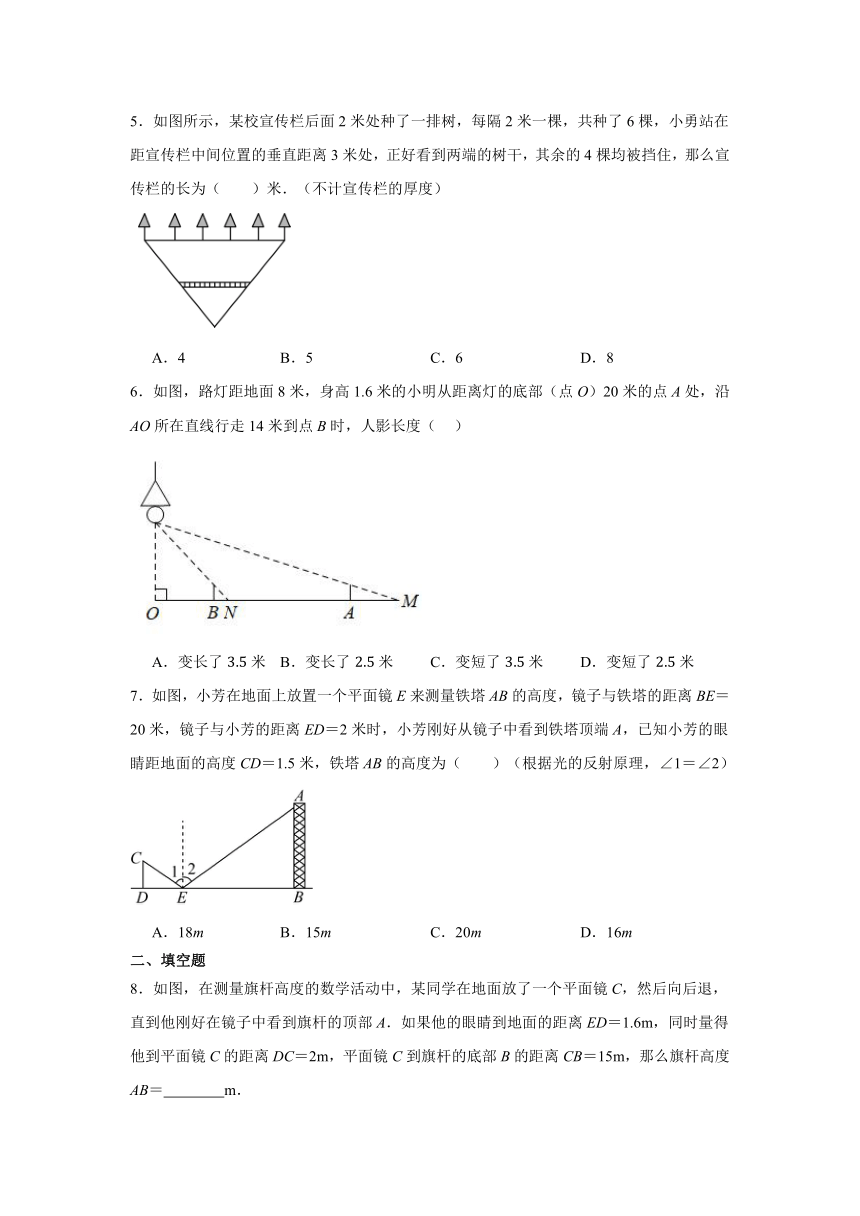
1.在同一时刻,身高1.6米的小丽在阳光下的影长为2.5米,一棵大树的影长为10米,则这棵树的高度为( )
A.3米 B.4.6米 C.6.4米 D.7.8米
2.《九章算术》中记载了一种测量古井水面以上部分深度的方法,如图所示,在井口处立一根垂直于井口的木杆,从木杆的顶端观察井水水岸.视线与井口的直径交于点,如果测得米,米,米,那么为( )
A.3米 B.4米 C.5米 D.6米
3.在一个边长为的正方体箱子的右侧面中心处点有一个小孔,在右侧面小孔正右方有一根点燃的蜡烛,如图小孔成像示意图.则像的长是( )
A. B. C. D.
4.如图,有一块锐角三角形材料,边,高,要把它加工成矩形零件,使其一边在上,其余两个顶点分别在,,且,则这个矩形零件的长为
A. B. C. D.
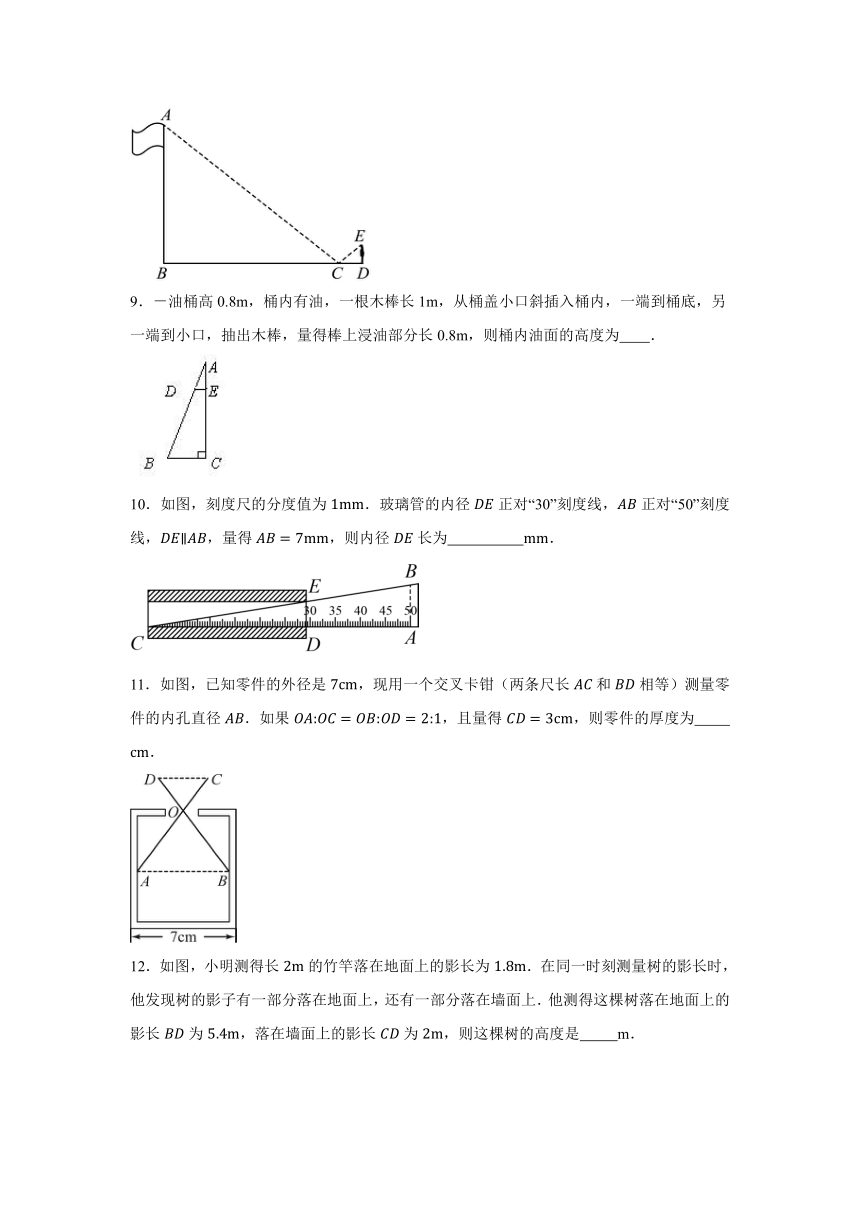
5.如图所示,某校宣传栏后面2米处种了一排树,每隔2米一棵,共种了6棵,小勇站在距宣传栏中间位置的垂直距离3米处,正好看到两端的树干,其余的4棵均被挡住,那么宣传栏的长为( )米.(不计宣传栏的厚度)
A.4 B.5 C.6 D.8
6.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿AO所在直线行走14米到点B时,人影长度( )
A.变长了米 B.变长了米 C.变短了米 D.变短了米
7.如图,小芳在地面上放置一个平面镜E来测量铁塔AB的高度,镜子与铁塔的距离BE=20米,镜子与小芳的距离ED=2米时,小芳刚好从镜子中看到铁塔顶端A,已知小芳的眼睛距地面的高度CD=1.5米,铁塔AB的高度为( )(根据光的反射原理,∠1=∠2)
A.18m B.15m C.20m D.16m
二、填空题
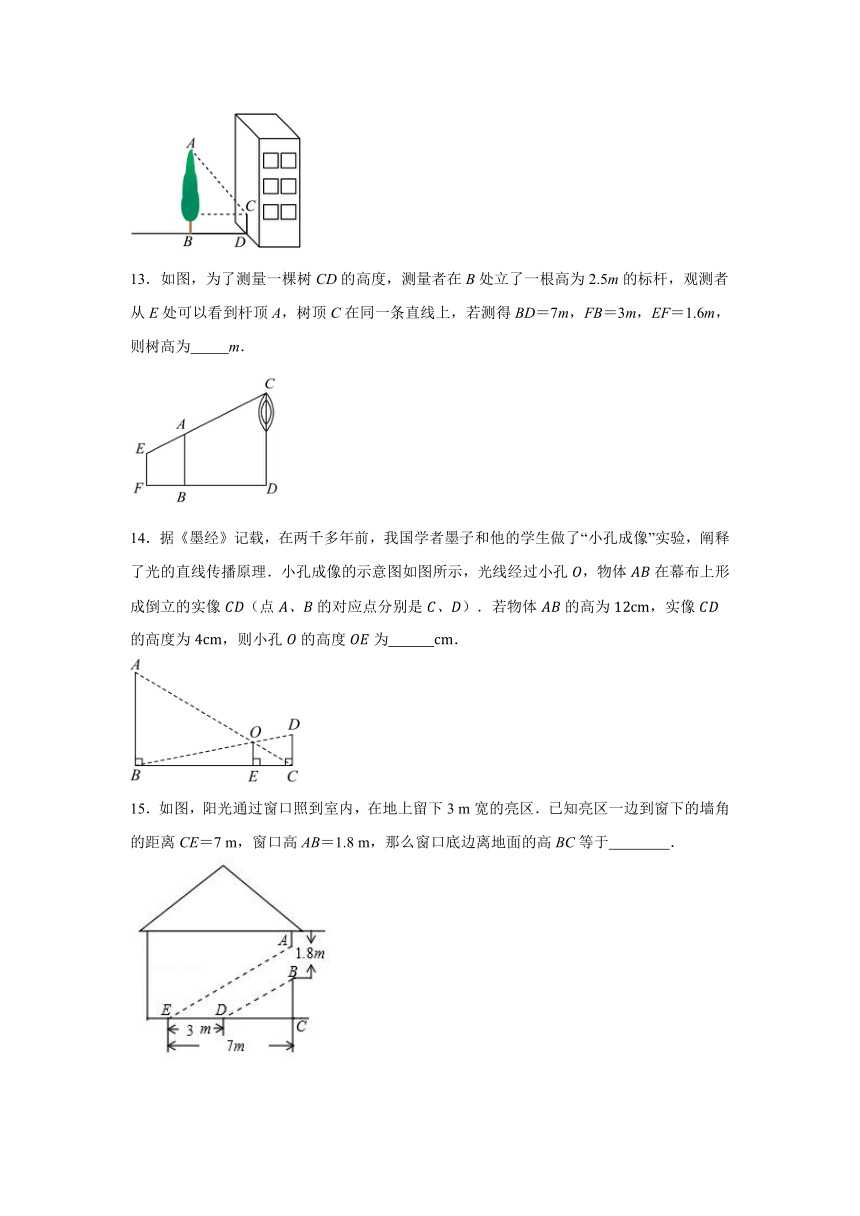
8.如图,在测量旗杆高度的数学活动中,某同学在地面放了一个平面镜C,然后向后退,直到他刚好在镜子中看到旗杆的顶部A.如果他的眼睛到地面的距离ED=1.6m,同时量得他到平面镜C的距离DC=2m,平面镜C到旗杆的底部B的距离CB=15m,那么旗杆高度AB= m.
9.-油桶高0.8m,桶内有油,一根木棒长1m,从桶盖小口斜插入桶内,一端到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长0.8m,则桶内油面的高度为 .
10.如图,刻度尺的分度值为.玻璃管的内径正对“30”刻度线,正对“50”刻度线,,量得,则内径长为 .
11.如图,已知零件的外径是,现用一个交叉卡钳(两条尺长和相等)测量零件的内孔直径.如果,且量得,则零件的厚度为 .
12.如图,小明测得长的竹竿落在地面上的影长为.在同一时刻测量树的影长时,他发现树的影子有一部分落在地面上,还有一部分落在墙面上.他测得这棵树落在地面上的影长为,落在墙面上的影长为,则这棵树的高度是 m.
13.如图,为了测量一棵树CD的高度,测量者在B处立了一根高为2.5m的标杆,观测者从E处可以看到杆顶A,树顶C在同一条直线上,若测得BD=7m,FB=3m,EF=1.6m,则树高为 m.
14.据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了“小孔成像”实验,阐释了光的直线传播原理.小孔成像的示意图如图所示,光线经过小孔,物体在幕布上形成倒立的实像(点的对应点分别是).若物体的高为,实像的高度为,则小孔的高度为 .
15.如图,阳光通过窗口照到室内,在地上留下3 m宽的亮区.已知亮区一边到窗下的墙角的距离CE=7 m,窗口高AB=1.8 m,那么窗口底边离地面的高BC等于 .
三、解答题
16.九(1)班同学到野外上数学活动课,为测量河的宽度(河的两岸平行),设计了如下方案:如图,同学们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在的延长线上取点,使得.经测量米,米,且点E到河岸的距离为6米.已知于点F,请你根据提供的数据,帮助他们计算河的宽度.
17.星明楼,又称新楼,位于榆林市南大街中心,如图①.小华为了解星明楼查阅资料发现星明楼的高度米,一天他实地观测星明楼,如图②,他在距星明楼30米(米)的F处,沿向点B前进,当走到点H处时,恰好看到广告牌的顶端C和楼顶A在一条直线上,小华的眼睛到地面的距离米,广告牌的高度米,米,点B、D、H、F在一条水平线上,,请求出小华从F处向前走了多少米恰好看到点C和点A在一条直线上(即求的长)?
18.如图:公路旁有两个高度相等的路灯AB、CD.小明同学上午上学时发现路灯B在太阳光下的影子恰好落到里程碑E处,他自己的影子恰好落在路灯CD的底部C处.晚自习放学时,站在上午同一个地方,发现在路灯CD的灯光下自己的影子恰好落在里程碑E处.
(1)在图中画出小明的位置,并画出光线,标明(太阳光、灯光).
(2)若AC距离为80米,小明身高为1.5米,小明离里程碑E恰好5米,求路灯高.
19.如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.
参考答案:
1.C
2.D
3.B
4.D
5.C
6.C
7.B
8.12
9.0.64m
10.4.2
11.
12.8
13.4.6
14.3
15.2.4 m
16.解:如图所示,过作于,
,
,
,
,
,,
,
又,
,
,即,
解得:,
桥的长度为8米.
17.解:如图:过点G作于点M,交于点N,
由题可得:,,
∵,
∴,
∴,
即,
解得:,
∴,
∴(米),
∴小华从F处向前走了8米恰好看到点C和点A在一条直线上.
18.解:
(1)如图,GH所在位置就是小明的位置,连结BE、DE,过C作CG∥BE与DE相交于点G,过G作GH⊥AC,即图中BE、CG是太阳光,DG为灯光;
(2)如图,GH所在位置就是小明的位置,
连结BE、DE,过C作CG∥BE与DE相交于点G,过G作GH⊥AC,即图中BE、CG是太阳光,DG为灯光;
∵GH⊥AC,CD⊥AC,
∴GH∥CD,
∴△EGH∽△EDC,
∴,
∵CG∥BE,
∴∠GCE=∠BEA,
∵GH⊥AC,AB⊥AC,
∴∠BAC=∠GHC=90°,
∵∠GCE=∠BEA,∠BAC=∠GHC,
∴△GCH∽△BEA,
∴,
根据题意可得GH=1.5米,EH=5米,AC=80米,AB=CD,可设AB=x米,
∵,,AB=CD,
∴,
∴,
将GH=1.5米,EH=5米,AC=80米,AB=CD,AB=x米代入和得,
,,
联立两式,解得x=6,
即AB=CD=6米,
路灯的高为6米;
19.解:延长CB交EF于点H,过点F作FM⊥EB的延长线于点M,
∵∠ABG=150°,BE⊥CB,
∴∠MBF=150°﹣90°=60°,
∴∠MFB=30°,
∵BF的长为2米,
∴BM=1米,MF=米.
∵BE⊥CB,MF⊥BE,
∴BH∥MF,
∴△EBH∽△EMF,
∴=.
又∵EB=1.8米,
∴=,
∴BH=.
∵BE∥CD,
∴△HBE∽△HCD,
∴=.
∵CB=5,
∴=,
∴CD=15.8米.
∴大树CD的高度为15.8米.
一、单选题
1.在同一时刻,身高1.6米的小丽在阳光下的影长为2.5米,一棵大树的影长为10米,则这棵树的高度为( )
A.3米 B.4.6米 C.6.4米 D.7.8米
2.《九章算术》中记载了一种测量古井水面以上部分深度的方法,如图所示,在井口处立一根垂直于井口的木杆,从木杆的顶端观察井水水岸.视线与井口的直径交于点,如果测得米,米,米,那么为( )
A.3米 B.4米 C.5米 D.6米
3.在一个边长为的正方体箱子的右侧面中心处点有一个小孔,在右侧面小孔正右方有一根点燃的蜡烛,如图小孔成像示意图.则像的长是( )
A. B. C. D.
4.如图,有一块锐角三角形材料,边,高,要把它加工成矩形零件,使其一边在上,其余两个顶点分别在,,且,则这个矩形零件的长为
A. B. C. D.
5.如图所示,某校宣传栏后面2米处种了一排树,每隔2米一棵,共种了6棵,小勇站在距宣传栏中间位置的垂直距离3米处,正好看到两端的树干,其余的4棵均被挡住,那么宣传栏的长为( )米.(不计宣传栏的厚度)
A.4 B.5 C.6 D.8
6.如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿AO所在直线行走14米到点B时,人影长度( )
A.变长了米 B.变长了米 C.变短了米 D.变短了米
7.如图,小芳在地面上放置一个平面镜E来测量铁塔AB的高度,镜子与铁塔的距离BE=20米,镜子与小芳的距离ED=2米时,小芳刚好从镜子中看到铁塔顶端A,已知小芳的眼睛距地面的高度CD=1.5米,铁塔AB的高度为( )(根据光的反射原理,∠1=∠2)
A.18m B.15m C.20m D.16m
二、填空题
8.如图,在测量旗杆高度的数学活动中,某同学在地面放了一个平面镜C,然后向后退,直到他刚好在镜子中看到旗杆的顶部A.如果他的眼睛到地面的距离ED=1.6m,同时量得他到平面镜C的距离DC=2m,平面镜C到旗杆的底部B的距离CB=15m,那么旗杆高度AB= m.
9.-油桶高0.8m,桶内有油,一根木棒长1m,从桶盖小口斜插入桶内,一端到桶底,另一端到小口,抽出木棒,量得棒上浸油部分长0.8m,则桶内油面的高度为 .
10.如图,刻度尺的分度值为.玻璃管的内径正对“30”刻度线,正对“50”刻度线,,量得,则内径长为 .
11.如图,已知零件的外径是,现用一个交叉卡钳(两条尺长和相等)测量零件的内孔直径.如果,且量得,则零件的厚度为 .
12.如图,小明测得长的竹竿落在地面上的影长为.在同一时刻测量树的影长时,他发现树的影子有一部分落在地面上,还有一部分落在墙面上.他测得这棵树落在地面上的影长为,落在墙面上的影长为,则这棵树的高度是 m.
13.如图,为了测量一棵树CD的高度,测量者在B处立了一根高为2.5m的标杆,观测者从E处可以看到杆顶A,树顶C在同一条直线上,若测得BD=7m,FB=3m,EF=1.6m,则树高为 m.
14.据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了“小孔成像”实验,阐释了光的直线传播原理.小孔成像的示意图如图所示,光线经过小孔,物体在幕布上形成倒立的实像(点的对应点分别是).若物体的高为,实像的高度为,则小孔的高度为 .
15.如图,阳光通过窗口照到室内,在地上留下3 m宽的亮区.已知亮区一边到窗下的墙角的距离CE=7 m,窗口高AB=1.8 m,那么窗口底边离地面的高BC等于 .
三、解答题
16.九(1)班同学到野外上数学活动课,为测量河的宽度(河的两岸平行),设计了如下方案:如图,同学们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在的延长线上取点,使得.经测量米,米,且点E到河岸的距离为6米.已知于点F,请你根据提供的数据,帮助他们计算河的宽度.
17.星明楼,又称新楼,位于榆林市南大街中心,如图①.小华为了解星明楼查阅资料发现星明楼的高度米,一天他实地观测星明楼,如图②,他在距星明楼30米(米)的F处,沿向点B前进,当走到点H处时,恰好看到广告牌的顶端C和楼顶A在一条直线上,小华的眼睛到地面的距离米,广告牌的高度米,米,点B、D、H、F在一条水平线上,,请求出小华从F处向前走了多少米恰好看到点C和点A在一条直线上(即求的长)?
18.如图:公路旁有两个高度相等的路灯AB、CD.小明同学上午上学时发现路灯B在太阳光下的影子恰好落到里程碑E处,他自己的影子恰好落在路灯CD的底部C处.晚自习放学时,站在上午同一个地方,发现在路灯CD的灯光下自己的影子恰好落在里程碑E处.
(1)在图中画出小明的位置,并画出光线,标明(太阳光、灯光).
(2)若AC距离为80米,小明身高为1.5米,小明离里程碑E恰好5米,求路灯高.
19.如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.
参考答案:
1.C
2.D
3.B
4.D
5.C
6.C
7.B
8.12
9.0.64m
10.4.2
11.
12.8
13.4.6
14.3
15.2.4 m
16.解:如图所示,过作于,
,
,
,
,
,,
,
又,
,
,即,
解得:,
桥的长度为8米.
17.解:如图:过点G作于点M,交于点N,
由题可得:,,
∵,
∴,
∴,
即,
解得:,
∴,
∴(米),
∴小华从F处向前走了8米恰好看到点C和点A在一条直线上.
18.解:
(1)如图,GH所在位置就是小明的位置,连结BE、DE,过C作CG∥BE与DE相交于点G,过G作GH⊥AC,即图中BE、CG是太阳光,DG为灯光;
(2)如图,GH所在位置就是小明的位置,
连结BE、DE,过C作CG∥BE与DE相交于点G,过G作GH⊥AC,即图中BE、CG是太阳光,DG为灯光;
∵GH⊥AC,CD⊥AC,
∴GH∥CD,
∴△EGH∽△EDC,
∴,
∵CG∥BE,
∴∠GCE=∠BEA,
∵GH⊥AC,AB⊥AC,
∴∠BAC=∠GHC=90°,
∵∠GCE=∠BEA,∠BAC=∠GHC,
∴△GCH∽△BEA,
∴,
根据题意可得GH=1.5米,EH=5米,AC=80米,AB=CD,可设AB=x米,
∵,,AB=CD,
∴,
∴,
将GH=1.5米,EH=5米,AC=80米,AB=CD,AB=x米代入和得,
,,
联立两式,解得x=6,
即AB=CD=6米,
路灯的高为6米;
19.解:延长CB交EF于点H,过点F作FM⊥EB的延长线于点M,
∵∠ABG=150°,BE⊥CB,
∴∠MBF=150°﹣90°=60°,
∴∠MFB=30°,
∵BF的长为2米,
∴BM=1米,MF=米.
∵BE⊥CB,MF⊥BE,
∴BH∥MF,
∴△EBH∽△EMF,
∴=.
又∵EB=1.8米,
∴=,
∴BH=.
∵BE∥CD,
∴△HBE∽△HCD,
∴=.
∵CB=5,
∴=,
∴CD=15.8米.
∴大树CD的高度为15.8米.
