湖北省恩施市沙地初中2024-2025学年八年级上学期数学10月测试题卷(含简略答案)
文档属性
| 名称 | 湖北省恩施市沙地初中2024-2025学年八年级上学期数学10月测试题卷(含简略答案) | 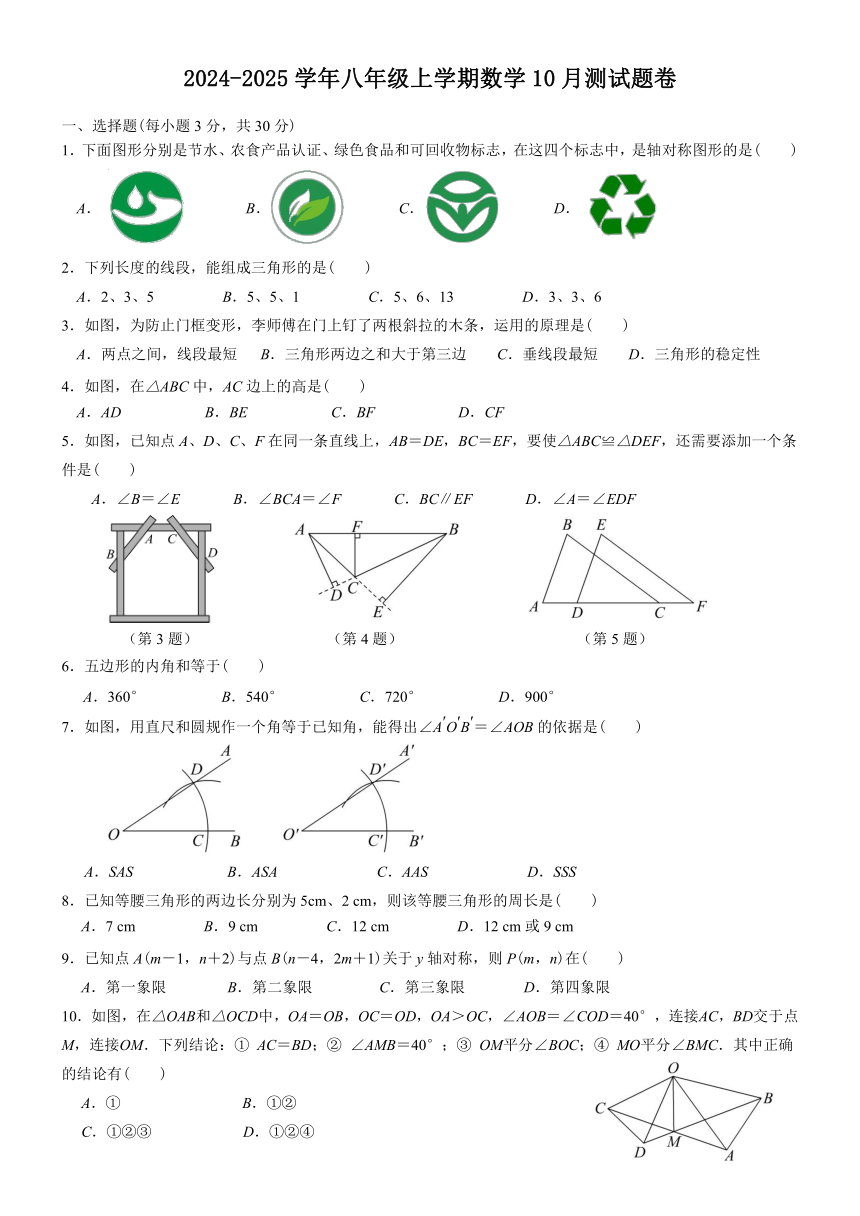 | |
| 格式 | doc | ||
| 文件大小 | 290.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-21 19:57:08 | ||
图片预览


文档简介
2024-2025学年八年级上学期数学10月测试题卷
一、选择题(每小题3分,共30分)
1.下面图形分别是节水、农食产品认证、绿色食品和可回收物标志,在这四个标志中,是轴对称图形的是( )
A. B. C. D.
2.下列长度的线段,能组成三角形的是( )
A.2、3、5 B.5、5、1 C.5、6、13 D.3、3、6
3.如图,为防止门框变形,李师傅在门上钉了两根斜拉的木条,运用的原理是( )
A.两点之间,线段最短 B.三角形两边之和大于第三边 C.垂线段最短 D.三角形的稳定性
4.如图,在△ABC中,AC边上的高是( )
A.AD B.BE C.BF D.CF
5.如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
A.∠B=∠E B.∠BCA=∠F C.BC∥EF D.∠A=∠EDF
(第3题) (第4题) (第5题)
6.五边形的内角和等于( )
A.360° B.540° C.720° D.900°
7.如图,用直尺和圆规作一个角等于已知角,能得出∠AOB=∠AOB的依据是( )
A.SAS B.ASA C.AAS D.SSS
8.已知等腰三角形的两边长分别为5cm、2 cm,则该等腰三角形的周长是( )
A.7 cm B.9 cm C.12 cm D.12 cm或9 cm
9.已知点A(m-1,n+2)与点B(n-4,2m+1)关于y轴对称,则P(m,n)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:① AC=BD;② ∠AMB=40°;③ OM平分∠BOC;④ MO平分∠BMC.其中正确的结论有( )
A.① B.①②
C.①②③ D.①②④
二、填空题(每小题3分,共18分)
11.一个三角形的三个内角的度数比是1 : 2 : 3,这个三角形是 三角形;
12.如图,在一个房间内,有一个长为2米的梯子(图中CM)斜靠在墙上,此时梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面的墙上,此时梯子的倾斜角为45°,那么MN的长是 米.
13.如图,△ABD≌△ACE,AD=8cm,AB=3cm,则BE= cm.
(第12题) (第13题)
14.从汽车的后视镜中看见某车车牌的后5位号码是:,则该车的后5位号码实际上 .
15.如图,等腰△ABC的底边BC长为6,面积是24,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点G为线段EF上一动点,则△CDG周长的最小值为 .
16.如图,∠ABC,∠ADC,的角平分线交于点F,若∠A=15°,∠C=65°则∠F的度数为 .
(第15题) (第16题)
三、解答题(共72分)
17.(8分)如果一个多边形的内角和是外角和的3倍还多180°,那么这个多边形的边数是多少.
18.(8分)如图,在△ABC中,∠ABC=82°,∠C=58°,BD⊥AC于D,AE平分∠CAB,BD与AE交于点F,求∠AFB.
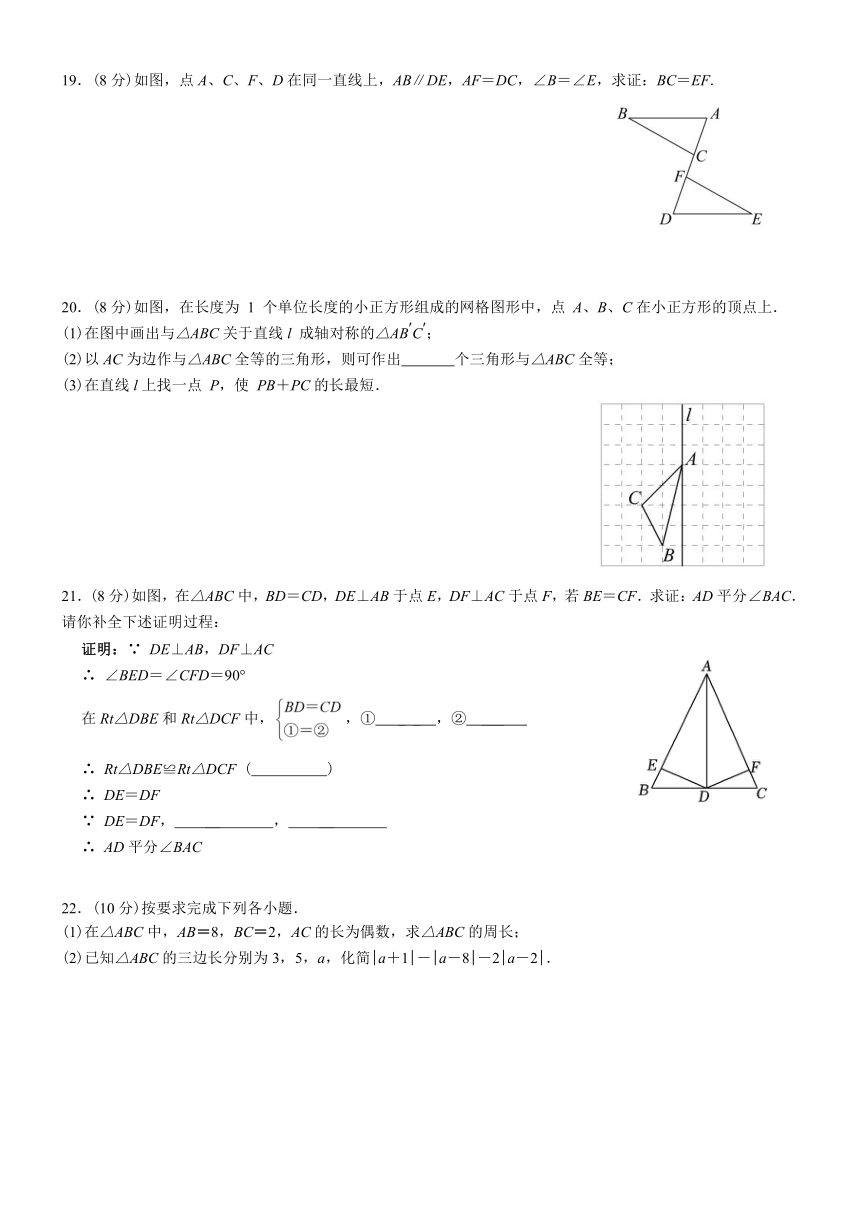
19.(8分)如图,点A、C、F、D在同一直线上,AB∥DE,AF=DC,∠B=∠E,求证:BC=EF.
20.(8分)如图,在长度为 1 个单位长度的小正方形组成的网格图形中,点 A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l 成轴对称的△ABC;
(2)以AC为边作与△ABC全等的三角形,则可作出 个三角形与△ABC全等;
(3)在直线l上找一点 P,使 PB+PC的长最短.
21.(8分)如图,在△ABC中,BD=CD,DE⊥AB于点E,DF⊥AC于点F,若BE=CF.求证:AD平分∠BAC.
请你补全下述证明过程:
证明:∵ DE⊥AB,DF⊥AC
∴ ∠BED=∠CFD=90°
在Rt△DBE和Rt△DCF中,,① _ _ ,② ___
∴ Rt△DBE≌Rt△DCF ( )
∴ DE=DF
∵ DE=DF, __ , __
∴ AD平分∠BAC
22.(10分)按要求完成下列各小题.
(1)在△ABC中,AB=8,BC=2,AC的长为偶数,求△ABC的周长;
(2)已知△ABC的三边长分别为3,5,a,化简|a+1|-|a-8|-2|a-2|.
23.(10分)如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.
(1)求证:AD⊥CF;
(2)连接AF,试判断△ACF的形状,并说明理由.
24.(10分)已知等边△ABC的边长为4cm,点P,Q分别从B,C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA,AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
(1)如图(1),当x为何值时,PQ∥AB;
(2)如图(2),若PQ⊥AC,求x;
(3)如图(3),当点Q在AB上运动时,PQ与△ABC的高AD交于点O,OQ与OP是否总是相等?请说明理由.
答案
1. C
2. B
3. D
4. B
5. A
6. B
7. D
8. C
9. A
10. D 提示:④作OH⊥AC,OG⊥BD,由两三角形全等,得面积相等,再得两高相等OH=OG,从而得到MO平分∠BMC
11. 直角 ;
12. 2 .
13. 5 .
14. BA629 .
15. 11 .
16. 25° .提示:连接DB并延长,先推导出∠ABC-∠ADC=80°,再利用8字形∠F+∠CBF=∠C+∠CDF
17. 9
18. 110°
19.如图,点A、C、F、D在同一直线上,AB∥DE,AF=DC,∠B=∠E,求证:BC=EF.
证明:略
20.(1)在图中画出与△ABC关于直线l 成轴对称的△ABC;
(2)以AC为边作与△ABC全等的三角形,则可作出 3 个三角形与△ABC全等;
(3)在直线l上找一点 P,使 PB+PC的长最短.
21.如图,在△ABC中,BD=CD,DE⊥AB于点E,DF⊥AC于点F,若BE=CF.求证:AD平分∠BAC.
请你补全下述证明过程:
证明:∵ DE⊥AB,DF⊥AC
∴ ∠BED=∠CFD=90°
在Rt△DBE和Rt△DCF中,,① _BE ,② __ CF
∴ Rt△DBE≌Rt△DCF ( HL )
∴ DE=DF
∵ DE=DF, DE⊥AB , DF⊥AC
∴ AD平分∠BAC
22.(1) 18
(2) -3
23.如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.
(1)求证:AD⊥CF;略
(2)连接AF,试判断△ACF的形状,并说明理由.等腰三角形(AF=CF)
24.(1)当x=时,PQ∥AB;
(2) x=
(3)相等,理由略(提示:作QH⊥AD于H)
一、选择题(每小题3分,共30分)
1.下面图形分别是节水、农食产品认证、绿色食品和可回收物标志,在这四个标志中,是轴对称图形的是( )
A. B. C. D.
2.下列长度的线段,能组成三角形的是( )
A.2、3、5 B.5、5、1 C.5、6、13 D.3、3、6
3.如图,为防止门框变形,李师傅在门上钉了两根斜拉的木条,运用的原理是( )
A.两点之间,线段最短 B.三角形两边之和大于第三边 C.垂线段最短 D.三角形的稳定性
4.如图,在△ABC中,AC边上的高是( )
A.AD B.BE C.BF D.CF
5.如图,已知点A、D、C、F在同一条直线上,AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加一个条件是( )
A.∠B=∠E B.∠BCA=∠F C.BC∥EF D.∠A=∠EDF
(第3题) (第4题) (第5题)
6.五边形的内角和等于( )
A.360° B.540° C.720° D.900°
7.如图,用直尺和圆规作一个角等于已知角,能得出∠AOB=∠AOB的依据是( )
A.SAS B.ASA C.AAS D.SSS
8.已知等腰三角形的两边长分别为5cm、2 cm,则该等腰三角形的周长是( )
A.7 cm B.9 cm C.12 cm D.12 cm或9 cm
9.已知点A(m-1,n+2)与点B(n-4,2m+1)关于y轴对称,则P(m,n)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:① AC=BD;② ∠AMB=40°;③ OM平分∠BOC;④ MO平分∠BMC.其中正确的结论有( )
A.① B.①②
C.①②③ D.①②④
二、填空题(每小题3分,共18分)
11.一个三角形的三个内角的度数比是1 : 2 : 3,这个三角形是 三角形;
12.如图,在一个房间内,有一个长为2米的梯子(图中CM)斜靠在墙上,此时梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面的墙上,此时梯子的倾斜角为45°,那么MN的长是 米.
13.如图,△ABD≌△ACE,AD=8cm,AB=3cm,则BE= cm.
(第12题) (第13题)
14.从汽车的后视镜中看见某车车牌的后5位号码是:,则该车的后5位号码实际上 .
15.如图,等腰△ABC的底边BC长为6,面积是24,腰AC的垂直平分线EF分别交AC,AB边于E,F点.若点D为BC边的中点,点G为线段EF上一动点,则△CDG周长的最小值为 .
16.如图,∠ABC,∠ADC,的角平分线交于点F,若∠A=15°,∠C=65°则∠F的度数为 .
(第15题) (第16题)
三、解答题(共72分)
17.(8分)如果一个多边形的内角和是外角和的3倍还多180°,那么这个多边形的边数是多少.
18.(8分)如图,在△ABC中,∠ABC=82°,∠C=58°,BD⊥AC于D,AE平分∠CAB,BD与AE交于点F,求∠AFB.
19.(8分)如图,点A、C、F、D在同一直线上,AB∥DE,AF=DC,∠B=∠E,求证:BC=EF.
20.(8分)如图,在长度为 1 个单位长度的小正方形组成的网格图形中,点 A、B、C在小正方形的顶点上.
(1)在图中画出与△ABC关于直线l 成轴对称的△ABC;
(2)以AC为边作与△ABC全等的三角形,则可作出 个三角形与△ABC全等;
(3)在直线l上找一点 P,使 PB+PC的长最短.
21.(8分)如图,在△ABC中,BD=CD,DE⊥AB于点E,DF⊥AC于点F,若BE=CF.求证:AD平分∠BAC.
请你补全下述证明过程:
证明:∵ DE⊥AB,DF⊥AC
∴ ∠BED=∠CFD=90°
在Rt△DBE和Rt△DCF中,,① _ _ ,② ___
∴ Rt△DBE≌Rt△DCF ( )
∴ DE=DF
∵ DE=DF, __ , __
∴ AD平分∠BAC
22.(10分)按要求完成下列各小题.
(1)在△ABC中,AB=8,BC=2,AC的长为偶数,求△ABC的周长;
(2)已知△ABC的三边长分别为3,5,a,化简|a+1|-|a-8|-2|a-2|.
23.(10分)如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.
(1)求证:AD⊥CF;
(2)连接AF,试判断△ACF的形状,并说明理由.
24.(10分)已知等边△ABC的边长为4cm,点P,Q分别从B,C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA,AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
(1)如图(1),当x为何值时,PQ∥AB;
(2)如图(2),若PQ⊥AC,求x;
(3)如图(3),当点Q在AB上运动时,PQ与△ABC的高AD交于点O,OQ与OP是否总是相等?请说明理由.
答案
1. C
2. B
3. D
4. B
5. A
6. B
7. D
8. C
9. A
10. D 提示:④作OH⊥AC,OG⊥BD,由两三角形全等,得面积相等,再得两高相等OH=OG,从而得到MO平分∠BMC
11. 直角 ;
12. 2 .
13. 5 .
14. BA629 .
15. 11 .
16. 25° .提示:连接DB并延长,先推导出∠ABC-∠ADC=80°,再利用8字形∠F+∠CBF=∠C+∠CDF
17. 9
18. 110°
19.如图,点A、C、F、D在同一直线上,AB∥DE,AF=DC,∠B=∠E,求证:BC=EF.
证明:略
20.(1)在图中画出与△ABC关于直线l 成轴对称的△ABC;
(2)以AC为边作与△ABC全等的三角形,则可作出 3 个三角形与△ABC全等;
(3)在直线l上找一点 P,使 PB+PC的长最短.
21.如图,在△ABC中,BD=CD,DE⊥AB于点E,DF⊥AC于点F,若BE=CF.求证:AD平分∠BAC.
请你补全下述证明过程:
证明:∵ DE⊥AB,DF⊥AC
∴ ∠BED=∠CFD=90°
在Rt△DBE和Rt△DCF中,,① _BE ,② __ CF
∴ Rt△DBE≌Rt△DCF ( HL )
∴ DE=DF
∵ DE=DF, DE⊥AB , DF⊥AC
∴ AD平分∠BAC
22.(1) 18
(2) -3
23.如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.
(1)求证:AD⊥CF;略
(2)连接AF,试判断△ACF的形状,并说明理由.等腰三角形(AF=CF)
24.(1)当x=时,PQ∥AB;
(2) x=
(3)相等,理由略(提示:作QH⊥AD于H)
同课章节目录
