冀教版六年级数学下册立体图形的体积整理复习(课件)(共19张PPT)
文档属性
| 名称 | 冀教版六年级数学下册立体图形的体积整理复习(课件)(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-21 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
立体图形的体积整理复习
冀教版六年级下册整理复习
立体图形所占空间的大小叫立体图形的体积。
立方厘米(cm ) 立方分米(dm ) 立方米(m )
什么是立体图形的体积?
常见的体积单位有哪些?
1000
1000
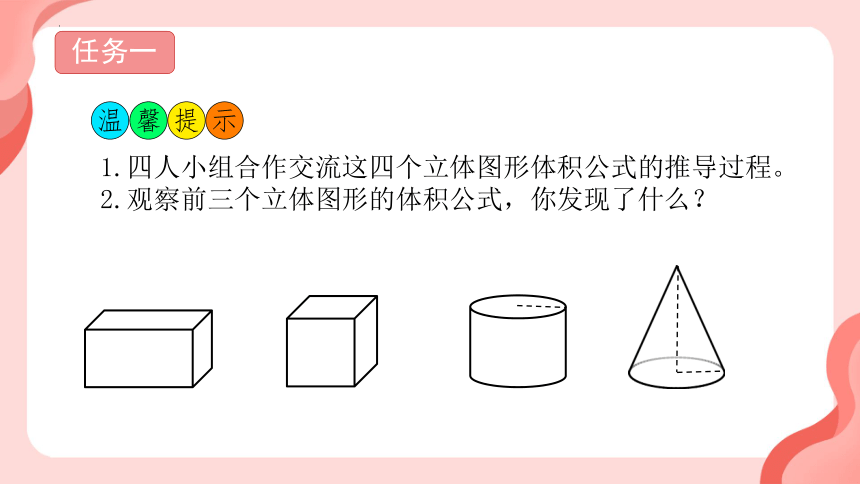
任务一
1.四人小组合作交流这四个立体图形体积公式的推导过程。
2.观察前三个立体图形的体积公式,你发现了什么?
温
馨
提
示
1立方厘米
长方体的体积
长方体的体积=长×宽×高
V=abh
底面积
×高
V=Sh
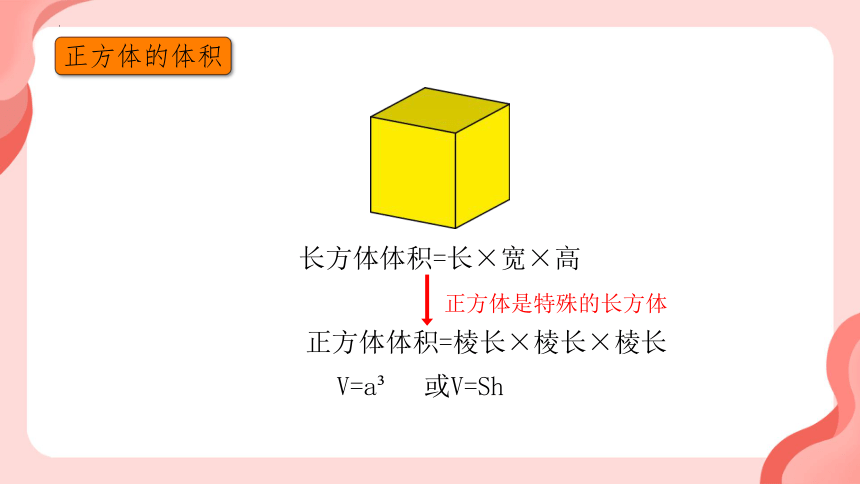
正方体的体积
V=a
或V=Sh
长方体体积=长×宽×高
正方体体积=棱长×棱长×棱长
正方体是特殊的长方体
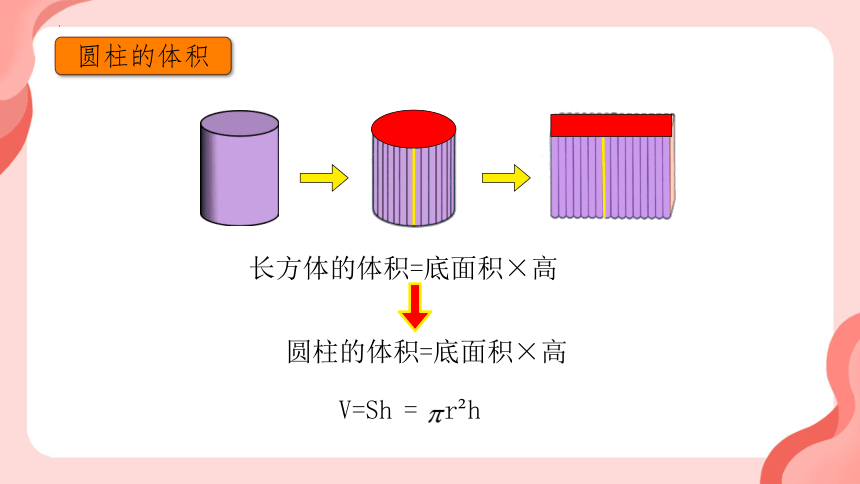
圆柱的体积
长方体的体积=底面积×高
圆柱的体积=底面积×高
V=Sh
= r
h
圆锥的体积
等底等高
圆锥的体积是等底等高的圆柱体积的 。
圆锥的体积= ×底面积×高
V= Sh=
r h
观察前三个立体图形的体积公式,你发现了什么?
V=Sh
转化思想
V=abh
V=a
V=Sh
V= Sh
V=Sh
V=Sh
任务二
1.运用公式,列出算式(不计算)
4
2
2
3
3
3
2
1
1
3
单位:cm
V=abh
=4×2×2
V=a
=3
=3×3×3
V=πr h
=3.14×1 ×2
V= πr h
= ×3.14×1 ×2
任务二
2.判断
(1)正方体是特殊的长方体。( )
(2)圆柱的体积是圆锥体积的3倍。( )
(3)棱长是6分米的正方体,它的表面积和体积相等。( )
(4)长方体、正方体、圆柱和圆锥的体积都可以用“底面积×高”计算。( )
(5)圆柱的底面半径越大,它的体积就越大。( )
√
×
×
×
×
等底等高
单位不同
圆柱的体积和半径、高都有联系
任务二
一个圆锥形沙堆,半径是2米,高3米。
走进生活
(1)求沙堆的体积。
(2)如果用这堆沙子铺一条宽2米,厚0.1米的路,能铺多长?
3m
2m
任务二
一个圆锥形沙堆,半径是2米,高3米。
走进生活
(1)求沙堆的体积。
3m
2m
任务二
一个圆锥形沙堆,半径是2米,高3米。
走进生活
(2)如果用这堆沙子铺一条宽2米,厚0.1米的路,能铺多长?
2m
0.1m
体积不变
3m
2m
任务二
这是一个正方体,棱长是20厘米。
走进生活
(1)求出正方体的体积。
(2)如果把这个正方体削成一个最大的圆柱,怎么削?圆柱的
体积是多少?
20cm
任务二
这是一个正方体,棱长是20厘米。
走进生活
(1)求出正方体的体积。
20cm
V=a
=20×20×20
=400×20
=8000(cm )
答:正方体的体积是8000立方厘米。
任务二
这是一个正方体,棱长是20厘米。
走进生活
(2)如果把这个正方体削成一个最大的圆柱,怎么削?圆柱的
体积是多少?
20cm
d= h=
d=20cm,h=20cm
r=d÷2=20÷2=10cm
V=πr h
=3.14×10 ×20
=314×20
=6280(cm )
图形 特征 表面积 (所有面的面积总和) 体积(立体图形所占空间的大小)
都有6个面,8个顶点,12条棱。 相对的棱相等;相对面是完全相同的长方形。 S表=(ab+ah+bh)×2 V长=abc V=sh
12条棱相等;6个面是完全相同的正方形。 S表=6a V正=a
底面都是圆;侧面都是曲面。 有3个面;底面是完全相同的两个圆;侧面沿高展开是长方形或正方形。 S表=2S底+S侧 其中: S底=πr S侧=Ch=πdh V圆柱=sh=πr h
有2个面;底面是圆;侧面展开是扇形 V圆锥= sh= πr h
容积(容器所能容纳物体的体积)
归纳整理立体图形的相关知识,形成思维表图。
同学们
上完这节课
你有什么新收获
立体图形的体积整理复习
冀教版六年级下册整理复习
立体图形所占空间的大小叫立体图形的体积。
立方厘米(cm ) 立方分米(dm ) 立方米(m )
什么是立体图形的体积?
常见的体积单位有哪些?
1000
1000
任务一
1.四人小组合作交流这四个立体图形体积公式的推导过程。
2.观察前三个立体图形的体积公式,你发现了什么?
温
馨
提
示
1立方厘米
长方体的体积
长方体的体积=长×宽×高
V=abh
底面积
×高
V=Sh
正方体的体积
V=a
或V=Sh
长方体体积=长×宽×高
正方体体积=棱长×棱长×棱长
正方体是特殊的长方体
圆柱的体积
长方体的体积=底面积×高
圆柱的体积=底面积×高
V=Sh
= r
h
圆锥的体积
等底等高
圆锥的体积是等底等高的圆柱体积的 。
圆锥的体积= ×底面积×高
V= Sh=
r h
观察前三个立体图形的体积公式,你发现了什么?
V=Sh
转化思想
V=abh
V=a
V=Sh
V= Sh
V=Sh
V=Sh
任务二
1.运用公式,列出算式(不计算)
4
2
2
3
3
3
2
1
1
3
单位:cm
V=abh
=4×2×2
V=a
=3
=3×3×3
V=πr h
=3.14×1 ×2
V= πr h
= ×3.14×1 ×2
任务二
2.判断
(1)正方体是特殊的长方体。( )
(2)圆柱的体积是圆锥体积的3倍。( )
(3)棱长是6分米的正方体,它的表面积和体积相等。( )
(4)长方体、正方体、圆柱和圆锥的体积都可以用“底面积×高”计算。( )
(5)圆柱的底面半径越大,它的体积就越大。( )
√
×
×
×
×
等底等高
单位不同
圆柱的体积和半径、高都有联系
任务二
一个圆锥形沙堆,半径是2米,高3米。
走进生活
(1)求沙堆的体积。
(2)如果用这堆沙子铺一条宽2米,厚0.1米的路,能铺多长?
3m
2m
任务二
一个圆锥形沙堆,半径是2米,高3米。
走进生活
(1)求沙堆的体积。
3m
2m
任务二
一个圆锥形沙堆,半径是2米,高3米。
走进生活
(2)如果用这堆沙子铺一条宽2米,厚0.1米的路,能铺多长?
2m
0.1m
体积不变
3m
2m
任务二
这是一个正方体,棱长是20厘米。
走进生活
(1)求出正方体的体积。
(2)如果把这个正方体削成一个最大的圆柱,怎么削?圆柱的
体积是多少?
20cm
任务二
这是一个正方体,棱长是20厘米。
走进生活
(1)求出正方体的体积。
20cm
V=a
=20×20×20
=400×20
=8000(cm )
答:正方体的体积是8000立方厘米。
任务二
这是一个正方体,棱长是20厘米。
走进生活
(2)如果把这个正方体削成一个最大的圆柱,怎么削?圆柱的
体积是多少?
20cm
d= h=
d=20cm,h=20cm
r=d÷2=20÷2=10cm
V=πr h
=3.14×10 ×20
=314×20
=6280(cm )
图形 特征 表面积 (所有面的面积总和) 体积(立体图形所占空间的大小)
都有6个面,8个顶点,12条棱。 相对的棱相等;相对面是完全相同的长方形。 S表=(ab+ah+bh)×2 V长=abc V=sh
12条棱相等;6个面是完全相同的正方形。 S表=6a V正=a
底面都是圆;侧面都是曲面。 有3个面;底面是完全相同的两个圆;侧面沿高展开是长方形或正方形。 S表=2S底+S侧 其中: S底=πr S侧=Ch=πdh V圆柱=sh=πr h
有2个面;底面是圆;侧面展开是扇形 V圆锥= sh= πr h
容积(容器所能容纳物体的体积)
归纳整理立体图形的相关知识,形成思维表图。
同学们
上完这节课
你有什么新收获
