2024年北京一零一中高三(上)统练三数学(PDF版,含答案)
文档属性
| 名称 | 2024年北京一零一中高三(上)统练三数学(PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 480.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-21 09:53:36 | ||
图片预览



文档简介
2024北京一零一中高三(上)统练三
数 学
班级: 学号: 姓名: 成绩:
一、选择题共 10 小题。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 在复平面内,复数 z 满足 iz=3-4i,则 z 的虚部为( )
(A)3i (B)-3i (C)3 (D)-3
2. 已知{ bn}是等比数列,若 = 3, = 27, 则 b 的值为( )
(A)9 (B)-9 (C)±9 (D)81
3. 已知函数 f(x)的导函数 f'(x)的图象如图所示,则 f(x)的极小值点为
( )
(A)x 和 x (B)x (C)x (D)x
4. 在同一个坐标系中,函数 ( ) = , ( ) =
, ( ) = 的部分图象可能是( )
5. 已知实数 a>b>c,abc≠0,则下列结论一定正确的是( )
1 1
( ) > (B) ab> bc ( ) < ( ) + > +
6. 设 a,b是非零向量,则“|a+b|=|a|-|b|”是“a∥b”的( )
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
3
7. 已知函数 ( ) = (2 + )( > 0, | | < )是奇函数,且 ( ) = 1,将 f(x)的图象上
4
所有点的横坐标变为原来的 2 倍,纵坐标不变,所得图象对应的函数为 g(x),则( )
(A)g(x)= sin x (B)g(x)=- sin x ( ) ( ) = cos ( + ) ( ) ( ) = cos ( )
4 4
8. 荀子《劝学》中说:“不积跬步,无以至千里;不积小流,无以成江海.”学习是日积月累的
过程,每天进步一点点,前进不止一小点.若甲、 乙两同学当下的知识储备量均为 a,甲同学
每天的“进步”率和乙同学每天的“退步”率均为 2%.n 天后,甲同学的知识储备量为(1+2%)na,乙
同学的知识储备量为(1-2%)na,则甲、乙的知识储备量之比为 2 时需要经过的天数约为( )
(参考数据: Ig2≈0.3010,Ig102≈2.0086,Ig98≈1.9912)
第1页/共3页
(A)15 (B)18 (C)30 (D)35
+1+ 9. 若数列{ an}满足 1 = 2,
= 2 + 3,则 + 的值为( )
+1
(A)9 (B)10 (C)11 (D)12
10. 2024 年 1 月 17 日我国自行研制的天舟七号货运飞船在发射 3 小时后成功对接于空间站天
和核心舱后向端口,创造了自动交会对接的记录.某学校的航天科技活动小组为了探索运动物
体追踪技术,设计了如下实验:目标 P 在地面轨道上做匀速直线运动;在地面上相距 7m 的 A,
B两点各放置一个传感器,分别实时记录 A,B两点与物体 P的距离.科技小组的同学根据传感
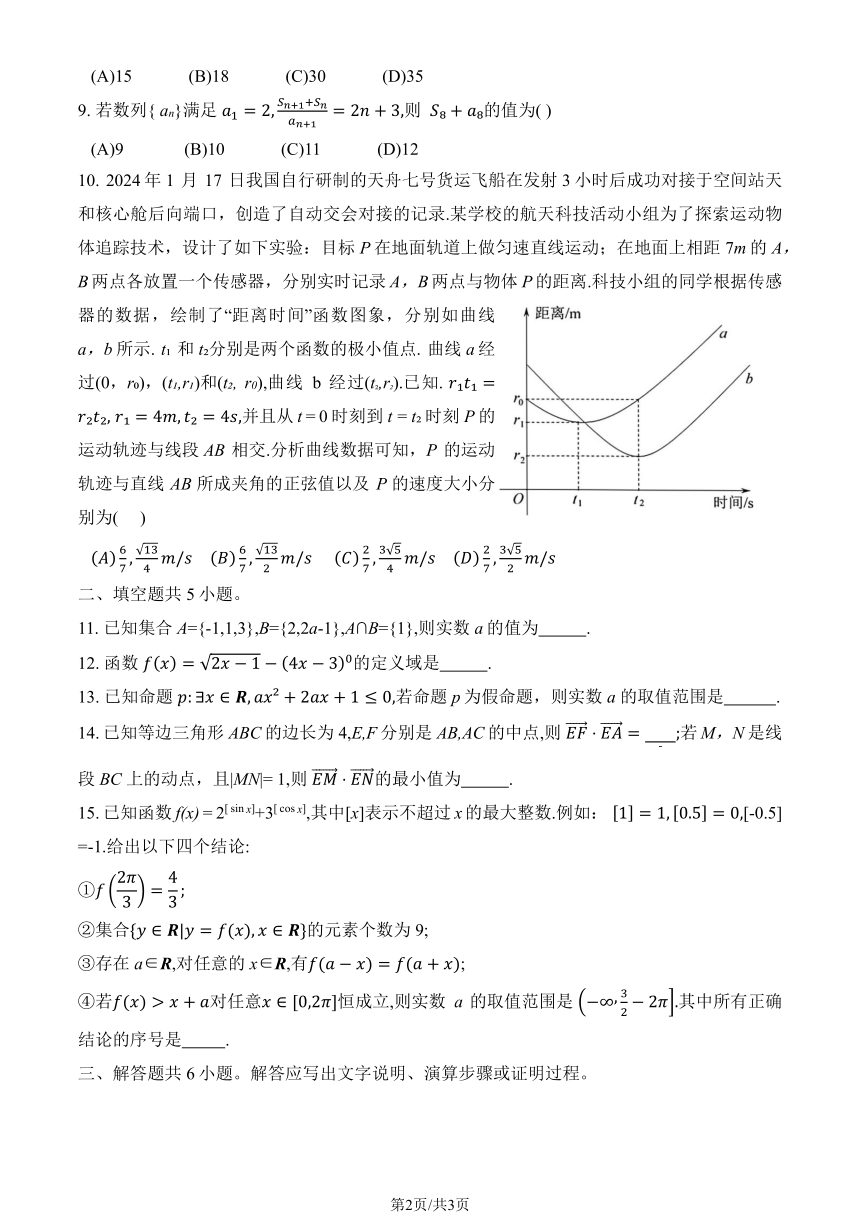
器的数据,绘制了“距离时间”函数图象,分别如曲线
a,b 所示. t 和 t 分别是两个函数的极小值点. 曲线 a 经
过(0,r ),(t ,r )和(t , r0),曲线 b 经过(t ,r ).已知. =
, = 4 , = 4 ,并且从 t = 0 时刻到 t = t 时刻 P 的
运动轨迹与线段 AB 相交.分析曲线数据可知,P 的运动
轨迹与直线 AB 所成夹角的正弦值以及 P 的速度大小分
别为( )
6 √13 6 √13 2 3√5 2 3√5
( ) , / ( ) , / ( ) , / ( ) , /
7 4 7 2 7 4 7 2
二、填空题共 5 小题。
11. 已知集合 A={-1,1,3},B={2,2a-1},A∩B={1},则实数 a 的值为 .
12. 函数 ( ) = √2 1 (4 3)0的定义域是 .
13. 已知命题 : ∈ , + 2 + 1 ≤ 0,若命题 p 为假命题,则实数 a 的取值范围是 .
14. 已知等边三角形 ABC 的边长为 4,E,F 分别是 AB,AC 的中点,则 = ;若 M,N 是线
段 BC 上的动点,且|MN|= 1,则 的最小值为 .
15. 已知函数 f(x) = 2[ sin x]+3[ cos x],其中[x]表示不超过 x的最大整数.例如: [1] = 1, [0.5] = 0,[-0.5]
=-1.给出以下四个结论:
2 4
① ( ) = ;
3 3
②集合{ ∈ | = ( ), ∈ }的元素个数为 9;
③存在 a∈R,对任意的 x∈R,有 ( ) = ( + );
3
④若 ( ) > + 对任意 ∈ [0,2 ]恒成立,则实数 a 的取值范围是 ( ∞, 2 ].其中所有正确
2
结论的序号是 .
三、解答题共 6 小题。解答应写出文字说明、演算步骤或证明过程。
第2页/共3页
16. 等差数列{ an}中,首项 = 1,且 + 2, , 2.成等比数列.
(1) 求数列{ an}的通项公式;
1
(2)求数列 { }的前 n 项和, ( ∈ ).
+1
17. 已知函数 ( ) = 2√3sin cos 2cos2 .
2 2 2
(1)求 ( )的值;
3
(2)求函数 f(x)的单调递减区间及对称轴方程.
18. 已知△ABC 中,角 A,B,C 所对的边分别为 a,b,c,且 + = 2 .
(1)求 A 的大小;
(2)若 D 是边 AB 的中点,且 CD=2,求( + 2√2 的取值范围.
1 1
19. 已知函数 ( ) = ( + 2) ( 2 ln ).
2
(1)求 f(x)的图象在点(1, (1))处的切线方程;
(2)讨论 f(x)的单调区间.
20. 已知 ( ) = (2 1) 在 x=0 处的切线方程为 + + = 0.
(1)求实数 a,b 的值;
3
(2)证明: f(x)仅有一个极值点 x ,且 ( 0) < ; 4
(3) 若 ( ) = ( 1) ,是否存在 m 使得 ( ) ≥ 1恒成立,若存在,请求出 m 的取值
范围;若不存在,请说明理由.
21. 有穷数列 , , … , ( > 2)中,令 ( , ) = , ,
+ +1 + + (1 ≤ ≤ ∈ ),当
= 时规定 ( , ) = .
(1)已知数列 3,2, 1,3,写出所有的有序数对( , ),且. < ,使得 ( , ) > 0;
(2) 已知整数列 1, 2, , , n 为偶数.若 ( , + 1) ( = 1, 2, , )满足:当 i 为奇数时, 2
( , + 1) > 0;当 i 为偶数时, ( , + 1) < 0.求 | 1| + | 2| + + | |的最小值;
(3) 已知数列 1, 2, , 满足. (1, ) > 0,定义集合 = { | ( + 1, ) > 0, = 1, 2,· · ·
, 1}..若 = { , , , }( ∈ 1 2 )且为非空集合,求证: (1, ) > + 1 + + . 2
第3页/共3页
北京一零一中 2024-2025学年度第一学期高三数学统练三参考答案
1. (2024门头沟一模 2) D
2. A
由题得 b24 = b2 · b6 = 3 × 27 = 81,而 b4 = b2 · q2 > 0,则 b4 = 9.
3. D
4. (2024海淀高一上期末 4) C
5. D
由题可知, a , 0, b , 0, c , 0, A项中,若 a > b > c > 0,则 a < a ,故 A项错误; B项中,
b c
若 a > 0 > b > c,则 ab < 0, bc > 0,故 ab < bc,故 B项错误; C项中,若 a > 0 > b > c,则
1 > 1 ,故 C项错误; D项中, ab + bc > ac + b2 ab ac > b2 bc a(b c) > b(b c),
a c
因为 a > b > c, abc , 0,则 b c > 0,故 ab + bc > ac + b2 正确,故 D项正确. 故选 D.
6. (2018东城二模理 5) A
7. (2023通州高三上期中 9) A
由题意可知 φ π= + kπ (k ∈ Z), |φ| < π,所以 φ π= 或 φ = π .
2 2 2
由 f ( 3π ) = 1 = A cos( 3π + φ) = 1,
4 2
因为 A > 0,所以 cos( 3π + φ) < 0,
2
所以 φ π= , A = 1,即 f (x) = cos(2x π ) = sin 2x,
2 2
故 g(x) = sin x.
8. (2024丰台高一上期末 9) B
9. B
S n+1 + S由 S nn+1 S n = an+1及 = 2n + 3得 S n+1 + S n = (2n + 3)(S n+1 S n),即 Sa n+1 + S n =n+1
S
{ }
(2n 3)S (2n 3)S ,即 (n 2)S (n 1)S ,所以 n
S n+1 S
+ n+1 + n + n = + n+1 = ,即
n 为常数
n + 1 n + 2 n + 1
S a S
列,又 1 1 1,所以 n= = = 1,即 S n = n + 1,所以 S 8 = 9, S 7 = 8, a8 = S 8 S 7 = 1,2 2 n + 1
所以 S 8 + a8 = 10.
10. B
北京一零一中 2024-2025学年度第一学期高三数学统练三参考答案 第 1页(共 5页)
{#{QQABAQIAogiIQAJAAQhCAQGACgMQkgACCQgGhBAEoAAACRNABAA=}#}
11. 1.
由题可得 2a 1 = 1,即 2a = 2,解得 a = 1.
12. [ 1 , 3 ) ∪ ( 3 ,+∞).
2 4 4
13. [0, 1).
因为 “ x ∈ R, ax2 + 2ax + 1 6 0”为假命题,所以其否定 “ x ∈ R, ax2 + 2ax + 1 > 0”为真a > 0,
命题,当 a = 0时,显然成立;当 a , 0时, ax2 + 2ax 1 + > 0恒成立,则 解4a2 4a < 0,
得 0 < a < 1. 综上,实数 a的取值范围是 [0, 1).
14. (2023大兴高三上期中 14) 2; 11 .
4
# – · # – # – # – # – # – # – # –EF EA = (EA + AF) · EA = EA2 + AF · EA = 22 + 2 × 2 ×
cos 120 = 2;若 M, N 是线段 BC 上的动点,且 |MN | = 1,
不妨设 N 点相对 M 更靠近 B点,设 |BN | = t (0 6 t 6 3),
# – · # – # – # –EM EN = (EB+BM) · # – # – # – # – # – # –(EB+BN) = EB2+(BM+BN) ·EB+
# – · # –BM BN = 22 + 2(t + t + 1) cos 120 + (t + 1)t = t2 t + 3 =
1 # – # –(t )2 11 ,当 t 1 时, EM · EN 取最小值,且为 11+ = .
2 4 2 4
15. (2021东城高三上期末 (改编) 15)①④.
16. (1)因为 a + 2, a , a 2成等比数列,所以 a22 3 4 3 = (a2 + 2)(a4 2),
即 (a + 2d)21 = (a1 + d + 2)(a1 + 3d 2),解得 d = 2,所以 an = 2n 1.
(2)因为 S 1 1n = + + · · · 1+ ,a1a2 a2a3 anan+1
所以 S 1 1 · · · 1n = 1 × +3 3 × + +5 (2n 1) × (2n + 1)
1
= × (1 1 1 1+ + · · · 1 1 ) 1 (1 1 ) n+ = = .
2 3 3 5 2n 1 2n + 1 2 2n + 1 2n + 1
17. (2015朝阳高三上期中理 15)
√ √
(1) f (x) = 2 3 sin x cos x 2 cos2 x = 3 sin x cos x 1 = 2 sin(x π ) 1.
2 2 2 6
f ( π ) = 2 sin π 1 = 0.
3 6
(2)由 2kπ π 6 x π 6 2kπ 3π+ + 得 2kπ 2π+ 6 x 6 2kπ 5π+ (k ∈ Z).
2 6 2 3 3
所以函数 f (x)的单调递减区间是 [2kπ 2π+ , 2kπ 5π+ ] (k ∈ Z).
3 3
令 x π kπ π 得 x kπ 2π= + = + (k ∈ Z).
6 2 3
所以函数 f (x)的对称轴方程是 x = kπ 2π+ (k ∈ Z).
3
北京一零一中 2024-2025学年度第一学期高三数学统练三参考答案 第 2页(共 5页)
{#{QQABAQIAogiIQAJAAQhCAQGACgMQkgACCQgGhBAEoAAACRNABAA=}#}
2
18. (1)由余弦定理得 cos A b + c
2 a2 2bc sin A
= = = sin A,
2bc 2bc
所以 tan A = 1.
又 A ∈ (0,π),所以 A 3π= .
4
(2)在 △ACD中,设 ∠ACD = α,则 ∠ADC π= α, α ∈ (0, π ).
4 4
c
2 b 2由正弦定理得 π = = ,sin sin( π α) sinα
√ 4 4 √
所以 b = 2 2 sin( π α), c = 4 2 sinα.
√ 4√
所以 c + 2 2b = 4 2 sinα + 8 sin( π α)
4
√ √ √ √
= 4 2 sin 2α + 8( cos 2α sinα) = 4 2 cosα.
2 √2
又 α ∈ (0, π ),所以 cosα ∈ ( 2 , 1),
√ 4 2 √
即 c + 2 2b的取值范围是 (4, 4 2).
19. (1) f ′(x) = a(1 12 ) (x
1 ), f ′(1) = 0, f (1) 1= .
x x 2
故 f (x)的图象在点 (1, f (1))处的切线方程为 y = 1 .
2
(2) f ′(x) = a(1 1 1 (x + 1)(x 1)2 ) (x ) = · (a x), x > 0.x x x2
①当 a 6 0时,令 f ′(x) = 0,解得 x = 1,有
x (0, 1) 1 (1,+∞)
f ′(x) + 0
f (x) ↗ 极小值 ↘
故单调递增区间为 (0, 1),单调递减区间为 (1,+∞).
②当 a > 0时,令 f ′(x) = 0,解得 x = 1或 x = a.
当 0 < a < 1时,
x (0, a) a (a, 1) 1 (1,+∞)
f ′(x) 0 + 0
f (x) ↘ 极小值 ↗ 极大值 ↘
故单调递增区间为 (a, 1),单调递减区间为 (0, a), (1,+∞)
当 a = 1时, f ′(x) 6 0, f (x)的单调递减区间为 (0,+∞),无单调递增区间.
北京一零一中 2024-2025学年度第一学期高三数学统练三参考答案 第 3页(共 5页)
{#{QQABAQIAogiIQAJAAQhCAQGACgMQkgACCQgGhBAEoAAACRNABAA=}#}
当 a > 1时,
x (0, 1) 1 (1, a) a (a,+∞)
f ′(x) 0 + 0
f (x) ↘ 极小值 ↗ 极大值 ↘
单调递增区间为 (1, a),单调递减区间为 (0, 1), (a,+∞).
20. (1) f (0) = 1, f ′(x) = 2eax + a(2x 1)eax 1,所以 f ′(0) = 1 a,
f (x)在 x = 0处的切线方程为 y + 1 = (1 a)x,所以 a = 2, b = 1.
(2) f (x) = (2x 1)e2x x, f ′(x) = 4xe2x 1,当 x < 0时, f ′(x) < 0, f (x)单调递减;
f ′′(x) = 4e2x + 8xe2x,当 x > 0时, f ′′(x) > 0, f ′(x)单调递增;
f ′
√
(0) = 1 < 0, f ′( 1 ) = e 1 > 0,所以存在 x0 ∈ (0, 1 )使得 f ′(x 2x04 4 0) = 0,即 4x0e = 1.
且当 x < x0 时, f ′(x) < 0, f (x)单调递减;
当 x > x0 时, f ′(x) > 0, f (x)单调递增,
2x 1
所以 f (x)仅有一个极值点 x0, f (x0) = (2x0 1)e2x0 x 0 x 10 = 0 = ( 1 + x0).4x0 2 4x0
因为 x 1 1 5 30 ∈ (0, ),所以 + x4 4x 0 > ,所以 f (x0) < .0 4 4
(3) g′(x) = m2xemx 1,
则当 x < 0时, g′(x) < 0, g(x)单调递减,所以 g(x) > g(0) = 1恒成立;
g′′(x) = m2(1 + mx)emx.
1
当 m > 0, x > 0时, g′′(x) > 0, g′(x)单调递增, g′(0) = 1 < 0, g′( 1 ) = e m2 1 > 0,m
所以存在 x0 ∈ (0, 1 )使得 g′2 (x0) = 0,当 x0 > x > 0时 g
′(x) < 0, g(x)单调递减,
m
g(x0) < g(0) = 1,不合题意;
当 m 6 0, x > 0时, mx 1 6 1,所以 (mx 1)emx 6 emx,
所以 g(2) 6 e2m 2 < 2,不合题意.
综上,不存在 m使得 g(x) > 1恒成立.
21. (2024东城一模 21)
(1) (1, 4), (2, 3), (2, 4), (3, 4).
(2)由已知得 S (k, n k + 1)与 S (k + 1, n k)异号,其中 k ∈ N , k 6 n 1.
2
由于 |ak + an k+1| = |S (k, n k + 1) S (k + 1, n k)| = |S (k, n k + 1)| + |S (k + 1, n k)| > 2,
因此 |ak| + |an k+1| > 2, k = 1, 2, · · · , n 1.2
北京一零一中 2024-2025学年度第一学期高三数学统练三参考答案 第 4页(共 5页)
{#{QQABAQIAogiIQAJAAQhCAQGACgMQkgACCQgGhBAEoAAACRNABAA=}#}
而 |a n | + |a n+1| > 1, k = 1, 2, · · · , n 1,所以 |a1| + |a2| + · · · + |an| > n 1.2 2 2
令 n = 2m. 当 m为奇数时,取 a1 = a3 = · · · = am = 1, a2 = a4 = · · · = am 1 = 1,
am+3 = am+5 = · · · = a2m = 1, am+2 = am+4 = · · · = a2m 1 = 1, am+1 = 0时,
有 |a1| + |a2| + · · · + |an| = n 1.
当 m为偶数时,取 a1 = a3 = · · · = am 1 = 1, a2 = a4 = · · · = am = 1,
am+3 = am+5 = · · · = a2m 1 = 1, am+2 = am+4 = · · · = a2m = 1, am+1 = 0时, |a1|+ |a2|+· · ·+ |an| =
n 1.
综上, |a1| + |a2| + · · · + |an|的最小值为 n 1.
(3)对于数列 a1, a2, · · · , an, A = {i1, i2, · · · , ik},不妨设 i1 < i2 < · · · < ik.
因此要证: S (1, n) > ai1 + ai2 + · · · + aik ,
①首先考虑 im+1 im > 2 (m = 1, 2, · · · , k 1), 2 6 i1 6 ik 6 n 1的情况,
由于 S (i1, n) 6 0, S (i1 + 1, n) > 0,所以 ai1 < 0.
同理 ai2 < 0, · · ·, aik < 0.
由已知 S (1, n) > 0,所以有 S (1, n) > ai1 + ai2 + · · · + aik .
②下面考虑 i1, i2, · · · , ik (i1 > 2)中有一段是连续的正整数的情况,
即 ip 1 < A, iq + 1 < A, im+1 im = 1, m = p, p + 1, · · · , q 1 (1 6 p 6 q 1 6 k 1).
由于 S (ip, n) S (iq + 1, n) = aip+1 + aip+2 + · · · + aiq ,
由已知 S (ip, n) S (iq + 1, n) < 0,这说明此连续的 q p项的和为负.
同理,当含有多段的连续正整数的情况时,每段的和为负.
再由①的结论可得: S (1, n) > ai1 + ai2 + · · · + aik .
③若在①,②中 i1 = 1, i2 = 2, · · ·, im = m, im + 1 < A,由于 S (im + 1, n) > 0,
此时去掉前 m项,则可转化为①,②的情况,
所以有 S (1, n) > ai1 + ai2 + · · · + aik .
④若 A = {1, 2, · · ·m} (m 6 n 1),则 am+1 + am+2 + · · · + an > 0,
所以此时有 S (1, n) > ai1 + ai2 + · · · + aik .
综上所述,结论成立.
北京一零一中 2024-2025学年度第一学期高三数学统练三参考答案 第 5页(共 5页)
{#{QQABAQIAogiIQAJAAQhCAQGACgMQkgACCQgGhBAEoAAACRNABAA=}#}
数 学
班级: 学号: 姓名: 成绩:
一、选择题共 10 小题。在每小题列出的四个选项中,选出符合题目要求的一项。
1. 在复平面内,复数 z 满足 iz=3-4i,则 z 的虚部为( )
(A)3i (B)-3i (C)3 (D)-3
2. 已知{ bn}是等比数列,若 = 3, = 27, 则 b 的值为( )
(A)9 (B)-9 (C)±9 (D)81
3. 已知函数 f(x)的导函数 f'(x)的图象如图所示,则 f(x)的极小值点为
( )
(A)x 和 x (B)x (C)x (D)x
4. 在同一个坐标系中,函数 ( ) = , ( ) =
, ( ) = 的部分图象可能是( )
5. 已知实数 a>b>c,abc≠0,则下列结论一定正确的是( )
1 1
( ) > (B) ab> bc ( ) < ( ) + > +
6. 设 a,b是非零向量,则“|a+b|=|a|-|b|”是“a∥b”的( )
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
3
7. 已知函数 ( ) = (2 + )( > 0, | | < )是奇函数,且 ( ) = 1,将 f(x)的图象上
4
所有点的横坐标变为原来的 2 倍,纵坐标不变,所得图象对应的函数为 g(x),则( )
(A)g(x)= sin x (B)g(x)=- sin x ( ) ( ) = cos ( + ) ( ) ( ) = cos ( )
4 4
8. 荀子《劝学》中说:“不积跬步,无以至千里;不积小流,无以成江海.”学习是日积月累的
过程,每天进步一点点,前进不止一小点.若甲、 乙两同学当下的知识储备量均为 a,甲同学
每天的“进步”率和乙同学每天的“退步”率均为 2%.n 天后,甲同学的知识储备量为(1+2%)na,乙
同学的知识储备量为(1-2%)na,则甲、乙的知识储备量之比为 2 时需要经过的天数约为( )
(参考数据: Ig2≈0.3010,Ig102≈2.0086,Ig98≈1.9912)
第1页/共3页
(A)15 (B)18 (C)30 (D)35
+1+ 9. 若数列{ an}满足 1 = 2,
= 2 + 3,则 + 的值为( )
+1
(A)9 (B)10 (C)11 (D)12
10. 2024 年 1 月 17 日我国自行研制的天舟七号货运飞船在发射 3 小时后成功对接于空间站天
和核心舱后向端口,创造了自动交会对接的记录.某学校的航天科技活动小组为了探索运动物
体追踪技术,设计了如下实验:目标 P 在地面轨道上做匀速直线运动;在地面上相距 7m 的 A,
B两点各放置一个传感器,分别实时记录 A,B两点与物体 P的距离.科技小组的同学根据传感
器的数据,绘制了“距离时间”函数图象,分别如曲线
a,b 所示. t 和 t 分别是两个函数的极小值点. 曲线 a 经
过(0,r ),(t ,r )和(t , r0),曲线 b 经过(t ,r ).已知. =
, = 4 , = 4 ,并且从 t = 0 时刻到 t = t 时刻 P 的
运动轨迹与线段 AB 相交.分析曲线数据可知,P 的运动
轨迹与直线 AB 所成夹角的正弦值以及 P 的速度大小分
别为( )
6 √13 6 √13 2 3√5 2 3√5
( ) , / ( ) , / ( ) , / ( ) , /
7 4 7 2 7 4 7 2
二、填空题共 5 小题。
11. 已知集合 A={-1,1,3},B={2,2a-1},A∩B={1},则实数 a 的值为 .
12. 函数 ( ) = √2 1 (4 3)0的定义域是 .
13. 已知命题 : ∈ , + 2 + 1 ≤ 0,若命题 p 为假命题,则实数 a 的取值范围是 .
14. 已知等边三角形 ABC 的边长为 4,E,F 分别是 AB,AC 的中点,则 = ;若 M,N 是线
段 BC 上的动点,且|MN|= 1,则 的最小值为 .
15. 已知函数 f(x) = 2[ sin x]+3[ cos x],其中[x]表示不超过 x的最大整数.例如: [1] = 1, [0.5] = 0,[-0.5]
=-1.给出以下四个结论:
2 4
① ( ) = ;
3 3
②集合{ ∈ | = ( ), ∈ }的元素个数为 9;
③存在 a∈R,对任意的 x∈R,有 ( ) = ( + );
3
④若 ( ) > + 对任意 ∈ [0,2 ]恒成立,则实数 a 的取值范围是 ( ∞, 2 ].其中所有正确
2
结论的序号是 .
三、解答题共 6 小题。解答应写出文字说明、演算步骤或证明过程。
第2页/共3页
16. 等差数列{ an}中,首项 = 1,且 + 2, , 2.成等比数列.
(1) 求数列{ an}的通项公式;
1
(2)求数列 { }的前 n 项和, ( ∈ ).
+1
17. 已知函数 ( ) = 2√3sin cos 2cos2 .
2 2 2
(1)求 ( )的值;
3
(2)求函数 f(x)的单调递减区间及对称轴方程.
18. 已知△ABC 中,角 A,B,C 所对的边分别为 a,b,c,且 + = 2 .
(1)求 A 的大小;
(2)若 D 是边 AB 的中点,且 CD=2,求( + 2√2 的取值范围.
1 1
19. 已知函数 ( ) = ( + 2) ( 2 ln ).
2
(1)求 f(x)的图象在点(1, (1))处的切线方程;
(2)讨论 f(x)的单调区间.
20. 已知 ( ) = (2 1) 在 x=0 处的切线方程为 + + = 0.
(1)求实数 a,b 的值;
3
(2)证明: f(x)仅有一个极值点 x ,且 ( 0) < ; 4
(3) 若 ( ) = ( 1) ,是否存在 m 使得 ( ) ≥ 1恒成立,若存在,请求出 m 的取值
范围;若不存在,请说明理由.
21. 有穷数列 , , … , ( > 2)中,令 ( , ) = , ,
+ +1 + + (1 ≤ ≤ ∈ ),当
= 时规定 ( , ) = .
(1)已知数列 3,2, 1,3,写出所有的有序数对( , ),且. < ,使得 ( , ) > 0;
(2) 已知整数列 1, 2, , , n 为偶数.若 ( , + 1) ( = 1, 2, , )满足:当 i 为奇数时, 2
( , + 1) > 0;当 i 为偶数时, ( , + 1) < 0.求 | 1| + | 2| + + | |的最小值;
(3) 已知数列 1, 2, , 满足. (1, ) > 0,定义集合 = { | ( + 1, ) > 0, = 1, 2,· · ·
, 1}..若 = { , , , }( ∈ 1 2 )且为非空集合,求证: (1, ) > + 1 + + . 2
第3页/共3页
北京一零一中 2024-2025学年度第一学期高三数学统练三参考答案
1. (2024门头沟一模 2) D
2. A
由题得 b24 = b2 · b6 = 3 × 27 = 81,而 b4 = b2 · q2 > 0,则 b4 = 9.
3. D
4. (2024海淀高一上期末 4) C
5. D
由题可知, a , 0, b , 0, c , 0, A项中,若 a > b > c > 0,则 a < a ,故 A项错误; B项中,
b c
若 a > 0 > b > c,则 ab < 0, bc > 0,故 ab < bc,故 B项错误; C项中,若 a > 0 > b > c,则
1 > 1 ,故 C项错误; D项中, ab + bc > ac + b2 ab ac > b2 bc a(b c) > b(b c),
a c
因为 a > b > c, abc , 0,则 b c > 0,故 ab + bc > ac + b2 正确,故 D项正确. 故选 D.
6. (2018东城二模理 5) A
7. (2023通州高三上期中 9) A
由题意可知 φ π= + kπ (k ∈ Z), |φ| < π,所以 φ π= 或 φ = π .
2 2 2
由 f ( 3π ) = 1 = A cos( 3π + φ) = 1,
4 2
因为 A > 0,所以 cos( 3π + φ) < 0,
2
所以 φ π= , A = 1,即 f (x) = cos(2x π ) = sin 2x,
2 2
故 g(x) = sin x.
8. (2024丰台高一上期末 9) B
9. B
S n+1 + S由 S nn+1 S n = an+1及 = 2n + 3得 S n+1 + S n = (2n + 3)(S n+1 S n),即 Sa n+1 + S n =n+1
S
{ }
(2n 3)S (2n 3)S ,即 (n 2)S (n 1)S ,所以 n
S n+1 S
+ n+1 + n + n = + n+1 = ,即
n 为常数
n + 1 n + 2 n + 1
S a S
列,又 1 1 1,所以 n= = = 1,即 S n = n + 1,所以 S 8 = 9, S 7 = 8, a8 = S 8 S 7 = 1,2 2 n + 1
所以 S 8 + a8 = 10.
10. B
北京一零一中 2024-2025学年度第一学期高三数学统练三参考答案 第 1页(共 5页)
{#{QQABAQIAogiIQAJAAQhCAQGACgMQkgACCQgGhBAEoAAACRNABAA=}#}
11. 1.
由题可得 2a 1 = 1,即 2a = 2,解得 a = 1.
12. [ 1 , 3 ) ∪ ( 3 ,+∞).
2 4 4
13. [0, 1).
因为 “ x ∈ R, ax2 + 2ax + 1 6 0”为假命题,所以其否定 “ x ∈ R, ax2 + 2ax + 1 > 0”为真a > 0,
命题,当 a = 0时,显然成立;当 a , 0时, ax2 + 2ax 1 + > 0恒成立,则 解4a2 4a < 0,
得 0 < a < 1. 综上,实数 a的取值范围是 [0, 1).
14. (2023大兴高三上期中 14) 2; 11 .
4
# – · # – # – # – # – # – # – # –EF EA = (EA + AF) · EA = EA2 + AF · EA = 22 + 2 × 2 ×
cos 120 = 2;若 M, N 是线段 BC 上的动点,且 |MN | = 1,
不妨设 N 点相对 M 更靠近 B点,设 |BN | = t (0 6 t 6 3),
# – · # – # – # –EM EN = (EB+BM) · # – # – # – # – # – # –(EB+BN) = EB2+(BM+BN) ·EB+
# – · # –BM BN = 22 + 2(t + t + 1) cos 120 + (t + 1)t = t2 t + 3 =
1 # – # –(t )2 11 ,当 t 1 时, EM · EN 取最小值,且为 11+ = .
2 4 2 4
15. (2021东城高三上期末 (改编) 15)①④.
16. (1)因为 a + 2, a , a 2成等比数列,所以 a22 3 4 3 = (a2 + 2)(a4 2),
即 (a + 2d)21 = (a1 + d + 2)(a1 + 3d 2),解得 d = 2,所以 an = 2n 1.
(2)因为 S 1 1n = + + · · · 1+ ,a1a2 a2a3 anan+1
所以 S 1 1 · · · 1n = 1 × +3 3 × + +5 (2n 1) × (2n + 1)
1
= × (1 1 1 1+ + · · · 1 1 ) 1 (1 1 ) n+ = = .
2 3 3 5 2n 1 2n + 1 2 2n + 1 2n + 1
17. (2015朝阳高三上期中理 15)
√ √
(1) f (x) = 2 3 sin x cos x 2 cos2 x = 3 sin x cos x 1 = 2 sin(x π ) 1.
2 2 2 6
f ( π ) = 2 sin π 1 = 0.
3 6
(2)由 2kπ π 6 x π 6 2kπ 3π+ + 得 2kπ 2π+ 6 x 6 2kπ 5π+ (k ∈ Z).
2 6 2 3 3
所以函数 f (x)的单调递减区间是 [2kπ 2π+ , 2kπ 5π+ ] (k ∈ Z).
3 3
令 x π kπ π 得 x kπ 2π= + = + (k ∈ Z).
6 2 3
所以函数 f (x)的对称轴方程是 x = kπ 2π+ (k ∈ Z).
3
北京一零一中 2024-2025学年度第一学期高三数学统练三参考答案 第 2页(共 5页)
{#{QQABAQIAogiIQAJAAQhCAQGACgMQkgACCQgGhBAEoAAACRNABAA=}#}
2
18. (1)由余弦定理得 cos A b + c
2 a2 2bc sin A
= = = sin A,
2bc 2bc
所以 tan A = 1.
又 A ∈ (0,π),所以 A 3π= .
4
(2)在 △ACD中,设 ∠ACD = α,则 ∠ADC π= α, α ∈ (0, π ).
4 4
c
2 b 2由正弦定理得 π = = ,sin sin( π α) sinα
√ 4 4 √
所以 b = 2 2 sin( π α), c = 4 2 sinα.
√ 4√
所以 c + 2 2b = 4 2 sinα + 8 sin( π α)
4
√ √ √ √
= 4 2 sin 2α + 8( cos 2α sinα) = 4 2 cosα.
2 √2
又 α ∈ (0, π ),所以 cosα ∈ ( 2 , 1),
√ 4 2 √
即 c + 2 2b的取值范围是 (4, 4 2).
19. (1) f ′(x) = a(1 12 ) (x
1 ), f ′(1) = 0, f (1) 1= .
x x 2
故 f (x)的图象在点 (1, f (1))处的切线方程为 y = 1 .
2
(2) f ′(x) = a(1 1 1 (x + 1)(x 1)2 ) (x ) = · (a x), x > 0.x x x2
①当 a 6 0时,令 f ′(x) = 0,解得 x = 1,有
x (0, 1) 1 (1,+∞)
f ′(x) + 0
f (x) ↗ 极小值 ↘
故单调递增区间为 (0, 1),单调递减区间为 (1,+∞).
②当 a > 0时,令 f ′(x) = 0,解得 x = 1或 x = a.
当 0 < a < 1时,
x (0, a) a (a, 1) 1 (1,+∞)
f ′(x) 0 + 0
f (x) ↘ 极小值 ↗ 极大值 ↘
故单调递增区间为 (a, 1),单调递减区间为 (0, a), (1,+∞)
当 a = 1时, f ′(x) 6 0, f (x)的单调递减区间为 (0,+∞),无单调递增区间.
北京一零一中 2024-2025学年度第一学期高三数学统练三参考答案 第 3页(共 5页)
{#{QQABAQIAogiIQAJAAQhCAQGACgMQkgACCQgGhBAEoAAACRNABAA=}#}
当 a > 1时,
x (0, 1) 1 (1, a) a (a,+∞)
f ′(x) 0 + 0
f (x) ↘ 极小值 ↗ 极大值 ↘
单调递增区间为 (1, a),单调递减区间为 (0, 1), (a,+∞).
20. (1) f (0) = 1, f ′(x) = 2eax + a(2x 1)eax 1,所以 f ′(0) = 1 a,
f (x)在 x = 0处的切线方程为 y + 1 = (1 a)x,所以 a = 2, b = 1.
(2) f (x) = (2x 1)e2x x, f ′(x) = 4xe2x 1,当 x < 0时, f ′(x) < 0, f (x)单调递减;
f ′′(x) = 4e2x + 8xe2x,当 x > 0时, f ′′(x) > 0, f ′(x)单调递增;
f ′
√
(0) = 1 < 0, f ′( 1 ) = e 1 > 0,所以存在 x0 ∈ (0, 1 )使得 f ′(x 2x04 4 0) = 0,即 4x0e = 1.
且当 x < x0 时, f ′(x) < 0, f (x)单调递减;
当 x > x0 时, f ′(x) > 0, f (x)单调递增,
2x 1
所以 f (x)仅有一个极值点 x0, f (x0) = (2x0 1)e2x0 x 0 x 10 = 0 = ( 1 + x0).4x0 2 4x0
因为 x 1 1 5 30 ∈ (0, ),所以 + x4 4x 0 > ,所以 f (x0) < .0 4 4
(3) g′(x) = m2xemx 1,
则当 x < 0时, g′(x) < 0, g(x)单调递减,所以 g(x) > g(0) = 1恒成立;
g′′(x) = m2(1 + mx)emx.
1
当 m > 0, x > 0时, g′′(x) > 0, g′(x)单调递增, g′(0) = 1 < 0, g′( 1 ) = e m2 1 > 0,m
所以存在 x0 ∈ (0, 1 )使得 g′2 (x0) = 0,当 x0 > x > 0时 g
′(x) < 0, g(x)单调递减,
m
g(x0) < g(0) = 1,不合题意;
当 m 6 0, x > 0时, mx 1 6 1,所以 (mx 1)emx 6 emx,
所以 g(2) 6 e2m 2 < 2,不合题意.
综上,不存在 m使得 g(x) > 1恒成立.
21. (2024东城一模 21)
(1) (1, 4), (2, 3), (2, 4), (3, 4).
(2)由已知得 S (k, n k + 1)与 S (k + 1, n k)异号,其中 k ∈ N , k 6 n 1.
2
由于 |ak + an k+1| = |S (k, n k + 1) S (k + 1, n k)| = |S (k, n k + 1)| + |S (k + 1, n k)| > 2,
因此 |ak| + |an k+1| > 2, k = 1, 2, · · · , n 1.2
北京一零一中 2024-2025学年度第一学期高三数学统练三参考答案 第 4页(共 5页)
{#{QQABAQIAogiIQAJAAQhCAQGACgMQkgACCQgGhBAEoAAACRNABAA=}#}
而 |a n | + |a n+1| > 1, k = 1, 2, · · · , n 1,所以 |a1| + |a2| + · · · + |an| > n 1.2 2 2
令 n = 2m. 当 m为奇数时,取 a1 = a3 = · · · = am = 1, a2 = a4 = · · · = am 1 = 1,
am+3 = am+5 = · · · = a2m = 1, am+2 = am+4 = · · · = a2m 1 = 1, am+1 = 0时,
有 |a1| + |a2| + · · · + |an| = n 1.
当 m为偶数时,取 a1 = a3 = · · · = am 1 = 1, a2 = a4 = · · · = am = 1,
am+3 = am+5 = · · · = a2m 1 = 1, am+2 = am+4 = · · · = a2m = 1, am+1 = 0时, |a1|+ |a2|+· · ·+ |an| =
n 1.
综上, |a1| + |a2| + · · · + |an|的最小值为 n 1.
(3)对于数列 a1, a2, · · · , an, A = {i1, i2, · · · , ik},不妨设 i1 < i2 < · · · < ik.
因此要证: S (1, n) > ai1 + ai2 + · · · + aik ,
①首先考虑 im+1 im > 2 (m = 1, 2, · · · , k 1), 2 6 i1 6 ik 6 n 1的情况,
由于 S (i1, n) 6 0, S (i1 + 1, n) > 0,所以 ai1 < 0.
同理 ai2 < 0, · · ·, aik < 0.
由已知 S (1, n) > 0,所以有 S (1, n) > ai1 + ai2 + · · · + aik .
②下面考虑 i1, i2, · · · , ik (i1 > 2)中有一段是连续的正整数的情况,
即 ip 1 < A, iq + 1 < A, im+1 im = 1, m = p, p + 1, · · · , q 1 (1 6 p 6 q 1 6 k 1).
由于 S (ip, n) S (iq + 1, n) = aip+1 + aip+2 + · · · + aiq ,
由已知 S (ip, n) S (iq + 1, n) < 0,这说明此连续的 q p项的和为负.
同理,当含有多段的连续正整数的情况时,每段的和为负.
再由①的结论可得: S (1, n) > ai1 + ai2 + · · · + aik .
③若在①,②中 i1 = 1, i2 = 2, · · ·, im = m, im + 1 < A,由于 S (im + 1, n) > 0,
此时去掉前 m项,则可转化为①,②的情况,
所以有 S (1, n) > ai1 + ai2 + · · · + aik .
④若 A = {1, 2, · · ·m} (m 6 n 1),则 am+1 + am+2 + · · · + an > 0,
所以此时有 S (1, n) > ai1 + ai2 + · · · + aik .
综上所述,结论成立.
北京一零一中 2024-2025学年度第一学期高三数学统练三参考答案 第 5页(共 5页)
{#{QQABAQIAogiIQAJAAQhCAQGACgMQkgACCQgGhBAEoAAACRNABAA=}#}
同课章节目录
