2025人教A版高中数学必修第二册强化练习题--8.3.1 棱柱、棱锥、棱台的表面积和体积
文档属性
| 名称 | 2025人教A版高中数学必修第二册强化练习题--8.3.1 棱柱、棱锥、棱台的表面积和体积 |

|
|
| 格式 | docx | ||
| 文件大小 | 441.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 09:25:32 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025人教A版高中数学必修第二册
8.3 简单几何体的表面积与体积
8.3.1 棱柱、棱锥、棱台的表面积和体积
基础过关练
题组一 棱柱、棱锥、棱台的表面积
1.(2024河南新乡封丘第一中学月考)已知一个直三棱柱的高为2,其底面ABC水平放置的直观图(斜二测画法)为△A'B'C',如图,其中O'A'=O'B'=O'C'=1,则此三棱柱的表面积为( )
A.4+4 B.8+4 C.8+4 D.8+8
2.(2024湖南岳阳湘阴二中月考)正方体的八个顶点中,有四个恰好为正四面体的顶点,则正方体的表面积与正四面体的表面积的比值为( )
A. B. C. D.
3.(2024广东广州期中)已知正四棱台上底面边长为2,下底面边长为4,高为3,则其表面积为( )
A.36 B.12+20 C.12+20 D.48
4.(2023安徽宿州期中)一房屋顶部可以看成一个正四棱锥,其底面四边形的对角线长是侧棱长的倍,则该正四棱锥的一个侧面面积与底面面积的比值为( )
A. B. C. D.
题组二 棱柱、棱锥、棱台的体积
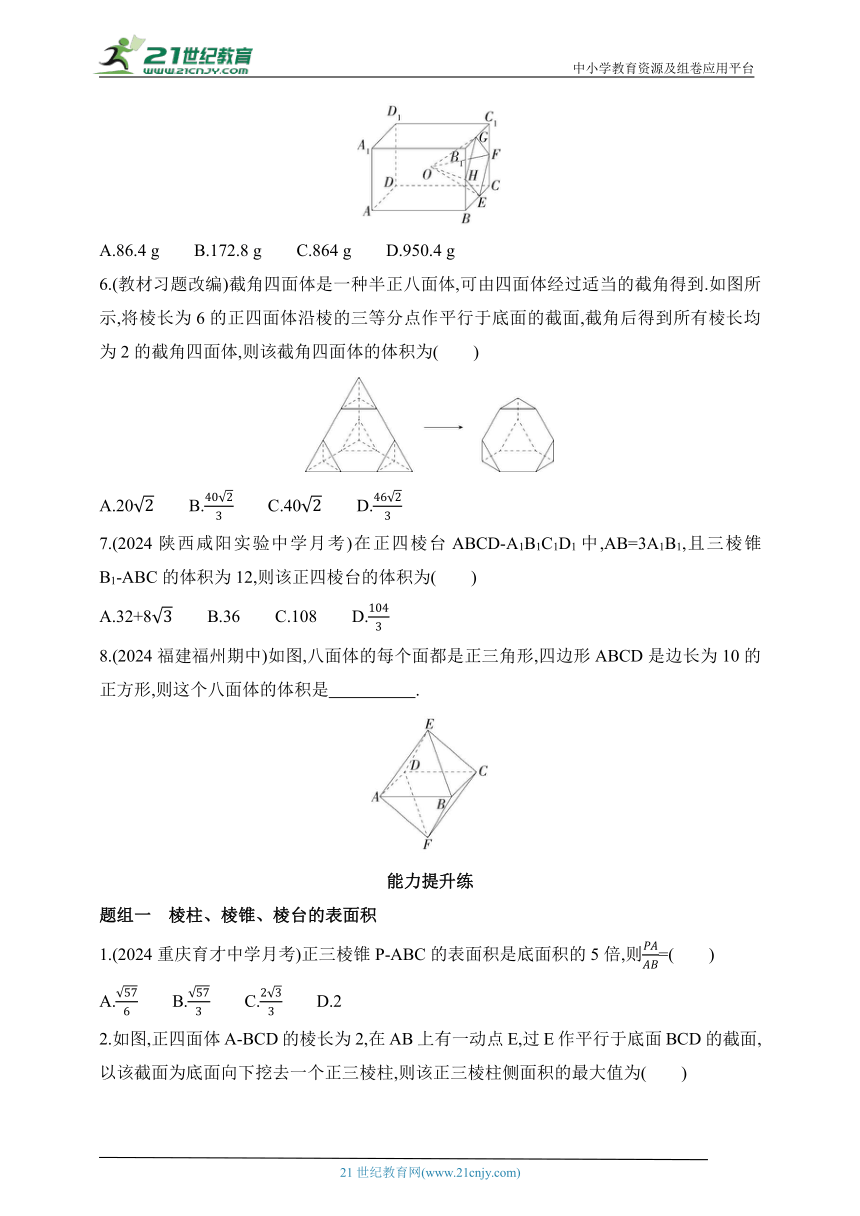
5.(2024四川南充期中)某校学生到一内燃机厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD-A1B1C1D1挖去四棱锥O-EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=12 cm,AA1=8 cm,3D打印所用原料密度为0.9 g/cm3,不考虑打印损耗,制作该模型所需原料的质量为( )
A.86.4 g B.172.8 g C.864 g D.950.4 g
6.(教材习题改编)截角四面体是一种半正八面体,可由四面体经过适当的截角得到.如图所示,将棱长为6的正四面体沿棱的三等分点作平行于底面的截面,截角后得到所有棱长均为2的截角四面体,则该截角四面体的体积为( )
A.20 B. C.40 D.
7.(2024陕西咸阳实验中学月考)在正四棱台ABCD-A1B1C1D1中,AB=3A1B1,且三棱锥B1-ABC的体积为12,则该正四棱台的体积为( )
A.32+8 B.36 C.108 D.
8.(2024福建福州期中)如图,八面体的每个面都是正三角形,四边形ABCD是边长为10的正方形,则这个八面体的体积是 .
能力提升练
题组一 棱柱、棱锥、棱台的表面积
1.(2024重庆育才中学月考)正三棱锥P-ABC的表面积是底面积的5倍,则=( )
A. B. C. D.2
2.如图,正四面体A-BCD的棱长为2,在AB上有一动点E,过E作平行于底面BCD的截面,以该截面为底面向下挖去一个正三棱柱,则该正三棱柱侧面积的最大值为( )
A. B. C. D.
3.(2022山西部分学校期末)在三棱锥P-ABC中,∠APB=
∠BPC=∠CPA=,且PA=PB=2,PC=4,则该三棱锥的表面积为( )
A.5+ B.3+2 C.5 D.5
4.(2024山西大学附属中学月考)已知正四棱锥的底面边长为2,现用一平行于正四棱锥底面的平面去截这个棱锥,截得的棱台的上、下底面的面积之比为1∶4,若截去的小正棱锥的侧棱长为2,则此棱台的表面积为 .
题组二 棱柱、棱锥、棱台的体积
5.(2024广东深圳月考)“方斗”常作为盛米的一种容器,其形状是一个上大下小的正四棱台,现有“方斗”容器如图所示,已知AB=2A1B1,现往容器里加米,当米的高度是“方斗”高度的一半时,用米38 kg,则该“方斗”可盛米的总质量为( )
A.152 kg B.133 kg C.114 kg D.112 kg
6.(2023湖北武汉水果湖高级中学联考)如图所示,在三棱柱ABC-A1B1C1中,E,F分别为AB,AC上靠近点A的三等分点,平面EB1C1F将三棱柱分成左、右两部分,左、右两部分的体积分别为V1和V2,那么V1∶V2=( )
A.7∶5 B.14∶13 C.5∶7 D.13∶14
7.(多选题)(2024浙江杭州西湖高级中学期中)如图,在直三棱柱ABC-A1B1C1中,AA1=2,AB=BC=1,∠ABC=90°,侧面AA1C1C的中心为O,点E是侧棱BB1上的一个动点,下列结论正确的是( )
A.直三棱柱的侧面积是4+2
B.直三棱柱的体积是
C.三棱锥E-AA1O的体积为定值
D.AE+EC1的最小值为2
答案与分层梯度式解析
8.3 简单几何体的表面积与体积
8.3.1 棱柱、棱锥、棱台的表面积和体积
基础过关练
1.C 2.B 3.B 4.B 5.D 6.D 7.D
1.C 由斜二测画法可得△ABC如图所示,其中OA=2,OB=OC=1,所以AB=AC=,所以所求三棱柱的表面积为2××2×2+(2+2)×2=8+4.故选C.
2.B 设正方体的棱长为a,则正四面体的棱长为a,正方体的表面积为6a2,正四面体的表面积为4××(a)2sin =2a2,
两者的比值为=,故选B.
3.B 如图,设正四棱台上、下底面的中心为O,O1,侧面上、下底边的中点为C,D,过C作CE⊥O1D,交O1D于点E,则O1O=3,OC=1,O1D=2,所以CD==,所以正四棱台的侧面积为××4=12,又正四棱台的上、下底面的面积和为22+42=20,所以正四棱台的表面积为20+12.故选B.
4.B 如图所示,将该房屋顶部看成正四棱锥P-ABCD,PO是四棱锥的高,
设AB=a,则底面四边形的对角线长为a,侧棱长为a,则正四棱锥P-ABCD的一个侧面的面积为a2,
又S四边形ABCD=a2,所以该正四棱锥的一个侧面面积与底面面积的比值为.故选B.
5.D 由题意得S四边形EFGH=8×12-4××4×6=48(cm2),且四棱锥O-EFGH的高为6 cm,所以VO-EFGH=×48×6=96(cm3),
又=12×12×8=1 152(cm3),
所以该模型的体积为1 152-96=1 056(cm3),故制作该模型所需原料的质量为1 056×0.9=950.4(g).故选D.
6.D 棱长为a的正四面体的底面正三角形的外接圆半径r=×a=a,
则该正四面体的高h==a,
所以该正四面体的体积V=×a2sin 60°×h=a2×a=a3,
所以该截角四面体的体积V'=×63-4××23=.故选D.
7.D 如图,
设正四棱台的高为h(h>0),则=S△ABC·h=12,∴S△ABC=,∴S正方形ABCD=2S△ABC=,
∵AB=3A1B1,∴=S正方形ABCD=,
故正四棱台的体积V=(S正方形ABCD++)·h=×·h=××h=.故选D.
8.答案
解析 由题意可知该八面体是由两个正四棱锥构成的,且正四棱锥的高h==5,
所以该八面体的体积V=2VE-ABCD=2××S正方形ABCD·h
=2××10×10×5=.
能力提升练
1.A 2.A 3.A 5.D 6.D 7.ACD
1.A 设正三棱锥的底面边长为a,侧棱长为b,则底面面积S1=a2,侧面积S2=3×a×,
因为表面积是底面积的5倍,所以侧面积是底面积的4倍,即4S1=S2,化简可得=a,即=,所以==.故选A.
2.A 过点E的正三棱柱如图所示,设其上、下底面的中心为O,O',底面边长为x,x∈(0,2),
由题意可知△AEG为正三角形,故AE=EG=x,
所以BE=2-x,
连接O'B,易知E'在O'B上,O'B=××2=,
O'E'=×x=,
故BE'=O'B-O'E'=-,
所以EE'===(2-x),
故该正三棱柱的侧面积S=3×(2-x)x=(2-x)·x=(-x2+2x)=-(x-1)2+,
所以当x=1时,S取得最大值.
故选A.
3.A 如图,因为PA=PB=2,∠APB=,
所以△PAB为等边三角形,AB=2,S△APB=×2×2×sin=.
在△PBC中,由余弦定理得BC2=PC2+PB2-2PB·PC·cos∠BPC=16+4-2×2×4×=12,
所以BC=2,同理可得AC=2.
因为BC2+PB2=PC2,AC2+PA2=PC2,
所以由勾股定理的逆定理可得BC⊥BP,AC⊥AP,
所以S△APC=S△BPC=×2×2=2.
取AB的中点M,连接CM,则AM=BM=1,
因为AC=BC=2,所以CM⊥AB,
故CM==,
故S△ABC=AB·CM=,
所以三棱锥P-ABC的表面积为5+.
故选A.
4.答案 5+3
解析 正四棱锥如图所示,设截面为四边形A1B1C1D1,
由题意可知,四边形A1B1C1D1与四边形ABCD相似且面积之比为1∶4,则===,又PA1=PB1=2,所以PA=PB=4,从而AA1=BB1=2,由AB=2,可得A1B1=1,作B1E⊥AB于E,则B1E为正四棱台ABCD-A1B1C1D1的斜高,易得B1E==.故此棱台的表面积为1×1+2×2+4××(1+2)×=5+3.
5.D 取AA1,BB1,CC1,DD1的中点分别为A2,B2,C2,D2,如图所示,
由题可知,四边形AA1B1B为等腰梯形,设A1B1=a,因为AB=2A1B1,所以A2B2==,
设棱台A1B1C1D1-A2B2C2D2的高为h,体积为V1,棱台A1B1C1D1-ABCD的体积为V,则棱台A1B1C1D1-ABCD的高为2h,
则V1=h=a2h,
V=(a2+4a2+2a2)·2h=a2h,所以=,
因为棱台A1B1C1D1-A2B2C2D2可盛米38 kg,
所以棱台A1B1C1D1-ABCD可盛米的总质量为×38=112(kg).故选D.
6.D 设三棱柱的高为h,一个底面的面积为S,体积为V,则V=V1+V2=Sh,
因为E,F分别为AB,AC上靠近点A的三等分点,
所以S△AEF=S,
则V1=h=Sh,
所以V2=V-V1=Sh,所以V1∶V2=13∶14.故选D.
7.ACD 由题意得,△ABC和△A1B1C1是等腰直角三角形,直三棱柱的侧面全是矩形,所以直三棱柱的侧面积为1×2×2+×2=4+2,故A正确;
直三棱柱的体积为S△ABC·AA1=×1×1×2=1,故B不正确;
易得==×BC×=×××2×1=,为定值,故C正确;
将侧面BB1C1C翻折至与平面AA1B1B在同一平面内,如图,则四边形AA1C1C为正方形,连接AC1,交BB1于点E,此时AE+EC1的值最小,为2,故D正确.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教A版高中数学必修第二册
8.3 简单几何体的表面积与体积
8.3.1 棱柱、棱锥、棱台的表面积和体积
基础过关练
题组一 棱柱、棱锥、棱台的表面积
1.(2024河南新乡封丘第一中学月考)已知一个直三棱柱的高为2,其底面ABC水平放置的直观图(斜二测画法)为△A'B'C',如图,其中O'A'=O'B'=O'C'=1,则此三棱柱的表面积为( )
A.4+4 B.8+4 C.8+4 D.8+8
2.(2024湖南岳阳湘阴二中月考)正方体的八个顶点中,有四个恰好为正四面体的顶点,则正方体的表面积与正四面体的表面积的比值为( )
A. B. C. D.
3.(2024广东广州期中)已知正四棱台上底面边长为2,下底面边长为4,高为3,则其表面积为( )
A.36 B.12+20 C.12+20 D.48
4.(2023安徽宿州期中)一房屋顶部可以看成一个正四棱锥,其底面四边形的对角线长是侧棱长的倍,则该正四棱锥的一个侧面面积与底面面积的比值为( )
A. B. C. D.
题组二 棱柱、棱锥、棱台的体积
5.(2024四川南充期中)某校学生到一内燃机厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD-A1B1C1D1挖去四棱锥O-EFGH后所得的几何体,其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=12 cm,AA1=8 cm,3D打印所用原料密度为0.9 g/cm3,不考虑打印损耗,制作该模型所需原料的质量为( )
A.86.4 g B.172.8 g C.864 g D.950.4 g
6.(教材习题改编)截角四面体是一种半正八面体,可由四面体经过适当的截角得到.如图所示,将棱长为6的正四面体沿棱的三等分点作平行于底面的截面,截角后得到所有棱长均为2的截角四面体,则该截角四面体的体积为( )
A.20 B. C.40 D.
7.(2024陕西咸阳实验中学月考)在正四棱台ABCD-A1B1C1D1中,AB=3A1B1,且三棱锥B1-ABC的体积为12,则该正四棱台的体积为( )
A.32+8 B.36 C.108 D.
8.(2024福建福州期中)如图,八面体的每个面都是正三角形,四边形ABCD是边长为10的正方形,则这个八面体的体积是 .
能力提升练
题组一 棱柱、棱锥、棱台的表面积
1.(2024重庆育才中学月考)正三棱锥P-ABC的表面积是底面积的5倍,则=( )
A. B. C. D.2
2.如图,正四面体A-BCD的棱长为2,在AB上有一动点E,过E作平行于底面BCD的截面,以该截面为底面向下挖去一个正三棱柱,则该正三棱柱侧面积的最大值为( )
A. B. C. D.
3.(2022山西部分学校期末)在三棱锥P-ABC中,∠APB=
∠BPC=∠CPA=,且PA=PB=2,PC=4,则该三棱锥的表面积为( )
A.5+ B.3+2 C.5 D.5
4.(2024山西大学附属中学月考)已知正四棱锥的底面边长为2,现用一平行于正四棱锥底面的平面去截这个棱锥,截得的棱台的上、下底面的面积之比为1∶4,若截去的小正棱锥的侧棱长为2,则此棱台的表面积为 .
题组二 棱柱、棱锥、棱台的体积
5.(2024广东深圳月考)“方斗”常作为盛米的一种容器,其形状是一个上大下小的正四棱台,现有“方斗”容器如图所示,已知AB=2A1B1,现往容器里加米,当米的高度是“方斗”高度的一半时,用米38 kg,则该“方斗”可盛米的总质量为( )
A.152 kg B.133 kg C.114 kg D.112 kg
6.(2023湖北武汉水果湖高级中学联考)如图所示,在三棱柱ABC-A1B1C1中,E,F分别为AB,AC上靠近点A的三等分点,平面EB1C1F将三棱柱分成左、右两部分,左、右两部分的体积分别为V1和V2,那么V1∶V2=( )
A.7∶5 B.14∶13 C.5∶7 D.13∶14
7.(多选题)(2024浙江杭州西湖高级中学期中)如图,在直三棱柱ABC-A1B1C1中,AA1=2,AB=BC=1,∠ABC=90°,侧面AA1C1C的中心为O,点E是侧棱BB1上的一个动点,下列结论正确的是( )
A.直三棱柱的侧面积是4+2
B.直三棱柱的体积是
C.三棱锥E-AA1O的体积为定值
D.AE+EC1的最小值为2
答案与分层梯度式解析
8.3 简单几何体的表面积与体积
8.3.1 棱柱、棱锥、棱台的表面积和体积
基础过关练
1.C 2.B 3.B 4.B 5.D 6.D 7.D
1.C 由斜二测画法可得△ABC如图所示,其中OA=2,OB=OC=1,所以AB=AC=,所以所求三棱柱的表面积为2××2×2+(2+2)×2=8+4.故选C.
2.B 设正方体的棱长为a,则正四面体的棱长为a,正方体的表面积为6a2,正四面体的表面积为4××(a)2sin =2a2,
两者的比值为=,故选B.
3.B 如图,设正四棱台上、下底面的中心为O,O1,侧面上、下底边的中点为C,D,过C作CE⊥O1D,交O1D于点E,则O1O=3,OC=1,O1D=2,所以CD==,所以正四棱台的侧面积为××4=12,又正四棱台的上、下底面的面积和为22+42=20,所以正四棱台的表面积为20+12.故选B.
4.B 如图所示,将该房屋顶部看成正四棱锥P-ABCD,PO是四棱锥的高,
设AB=a,则底面四边形的对角线长为a,侧棱长为a,则正四棱锥P-ABCD的一个侧面的面积为a2,
又S四边形ABCD=a2,所以该正四棱锥的一个侧面面积与底面面积的比值为.故选B.
5.D 由题意得S四边形EFGH=8×12-4××4×6=48(cm2),且四棱锥O-EFGH的高为6 cm,所以VO-EFGH=×48×6=96(cm3),
又=12×12×8=1 152(cm3),
所以该模型的体积为1 152-96=1 056(cm3),故制作该模型所需原料的质量为1 056×0.9=950.4(g).故选D.
6.D 棱长为a的正四面体的底面正三角形的外接圆半径r=×a=a,
则该正四面体的高h==a,
所以该正四面体的体积V=×a2sin 60°×h=a2×a=a3,
所以该截角四面体的体积V'=×63-4××23=.故选D.
7.D 如图,
设正四棱台的高为h(h>0),则=S△ABC·h=12,∴S△ABC=,∴S正方形ABCD=2S△ABC=,
∵AB=3A1B1,∴=S正方形ABCD=,
故正四棱台的体积V=(S正方形ABCD++)·h=×·h=××h=.故选D.
8.答案
解析 由题意可知该八面体是由两个正四棱锥构成的,且正四棱锥的高h==5,
所以该八面体的体积V=2VE-ABCD=2××S正方形ABCD·h
=2××10×10×5=.
能力提升练
1.A 2.A 3.A 5.D 6.D 7.ACD
1.A 设正三棱锥的底面边长为a,侧棱长为b,则底面面积S1=a2,侧面积S2=3×a×,
因为表面积是底面积的5倍,所以侧面积是底面积的4倍,即4S1=S2,化简可得=a,即=,所以==.故选A.
2.A 过点E的正三棱柱如图所示,设其上、下底面的中心为O,O',底面边长为x,x∈(0,2),
由题意可知△AEG为正三角形,故AE=EG=x,
所以BE=2-x,
连接O'B,易知E'在O'B上,O'B=××2=,
O'E'=×x=,
故BE'=O'B-O'E'=-,
所以EE'===(2-x),
故该正三棱柱的侧面积S=3×(2-x)x=(2-x)·x=(-x2+2x)=-(x-1)2+,
所以当x=1时,S取得最大值.
故选A.
3.A 如图,因为PA=PB=2,∠APB=,
所以△PAB为等边三角形,AB=2,S△APB=×2×2×sin=.
在△PBC中,由余弦定理得BC2=PC2+PB2-2PB·PC·cos∠BPC=16+4-2×2×4×=12,
所以BC=2,同理可得AC=2.
因为BC2+PB2=PC2,AC2+PA2=PC2,
所以由勾股定理的逆定理可得BC⊥BP,AC⊥AP,
所以S△APC=S△BPC=×2×2=2.
取AB的中点M,连接CM,则AM=BM=1,
因为AC=BC=2,所以CM⊥AB,
故CM==,
故S△ABC=AB·CM=,
所以三棱锥P-ABC的表面积为5+.
故选A.
4.答案 5+3
解析 正四棱锥如图所示,设截面为四边形A1B1C1D1,
由题意可知,四边形A1B1C1D1与四边形ABCD相似且面积之比为1∶4,则===,又PA1=PB1=2,所以PA=PB=4,从而AA1=BB1=2,由AB=2,可得A1B1=1,作B1E⊥AB于E,则B1E为正四棱台ABCD-A1B1C1D1的斜高,易得B1E==.故此棱台的表面积为1×1+2×2+4××(1+2)×=5+3.
5.D 取AA1,BB1,CC1,DD1的中点分别为A2,B2,C2,D2,如图所示,
由题可知,四边形AA1B1B为等腰梯形,设A1B1=a,因为AB=2A1B1,所以A2B2==,
设棱台A1B1C1D1-A2B2C2D2的高为h,体积为V1,棱台A1B1C1D1-ABCD的体积为V,则棱台A1B1C1D1-ABCD的高为2h,
则V1=h=a2h,
V=(a2+4a2+2a2)·2h=a2h,所以=,
因为棱台A1B1C1D1-A2B2C2D2可盛米38 kg,
所以棱台A1B1C1D1-ABCD可盛米的总质量为×38=112(kg).故选D.
6.D 设三棱柱的高为h,一个底面的面积为S,体积为V,则V=V1+V2=Sh,
因为E,F分别为AB,AC上靠近点A的三等分点,
所以S△AEF=S,
则V1=h=Sh,
所以V2=V-V1=Sh,所以V1∶V2=13∶14.故选D.
7.ACD 由题意得,△ABC和△A1B1C1是等腰直角三角形,直三棱柱的侧面全是矩形,所以直三棱柱的侧面积为1×2×2+×2=4+2,故A正确;
直三棱柱的体积为S△ABC·AA1=×1×1×2=1,故B不正确;
易得==×BC×=×××2×1=,为定值,故C正确;
将侧面BB1C1C翻折至与平面AA1B1B在同一平面内,如图,则四边形AA1C1C为正方形,连接AC1,交BB1于点E,此时AE+EC1的值最小,为2,故D正确.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
