2025人教A版高中数学必修第二册强化练习题--8.5.2 直线与平面平行
文档属性
| 名称 | 2025人教A版高中数学必修第二册强化练习题--8.5.2 直线与平面平行 |  | |
| 格式 | docx | ||
| 文件大小 | 631.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 09:25:32 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025人教A版高中数学必修第二册
8.5.2 直线与平面平行
基础过关练
题组一 直线与平面平行的判定
1.(多选题)(2024陕西咸阳期中)已知a,b是不同的直线,α是平面,下列命题错误的是( )
A.a∥b,b α a∥α
B.a∥α,b α a∥b
C.a∥α,a∥b b∥α
D.a α,a∥b,b α a∥α
2.(多选题)(2024广东湛江雷州第二中学月考)如图所示,P为矩形ABCD所在平面外一点,矩形对角线的交点为O,M为PB的中点,则以下结论正确的是( )
OM∥PD B.OM∥平面PAC
C.OM∥平面PDA D.OM∥平面PBA
3.(2024河北沧州期中)如图,直三棱柱ABC-A1B1C1的所有棱长都为1,D,E分别为B1C1和AB1的中点,则DE与平面A1ACC1的位置关系是 ,三棱锥C1-AA1B1的体积为 .
4.如图所示,在正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN,求证:MN∥平面ABB1A1.
题组二 直线与平面平行的性质定理
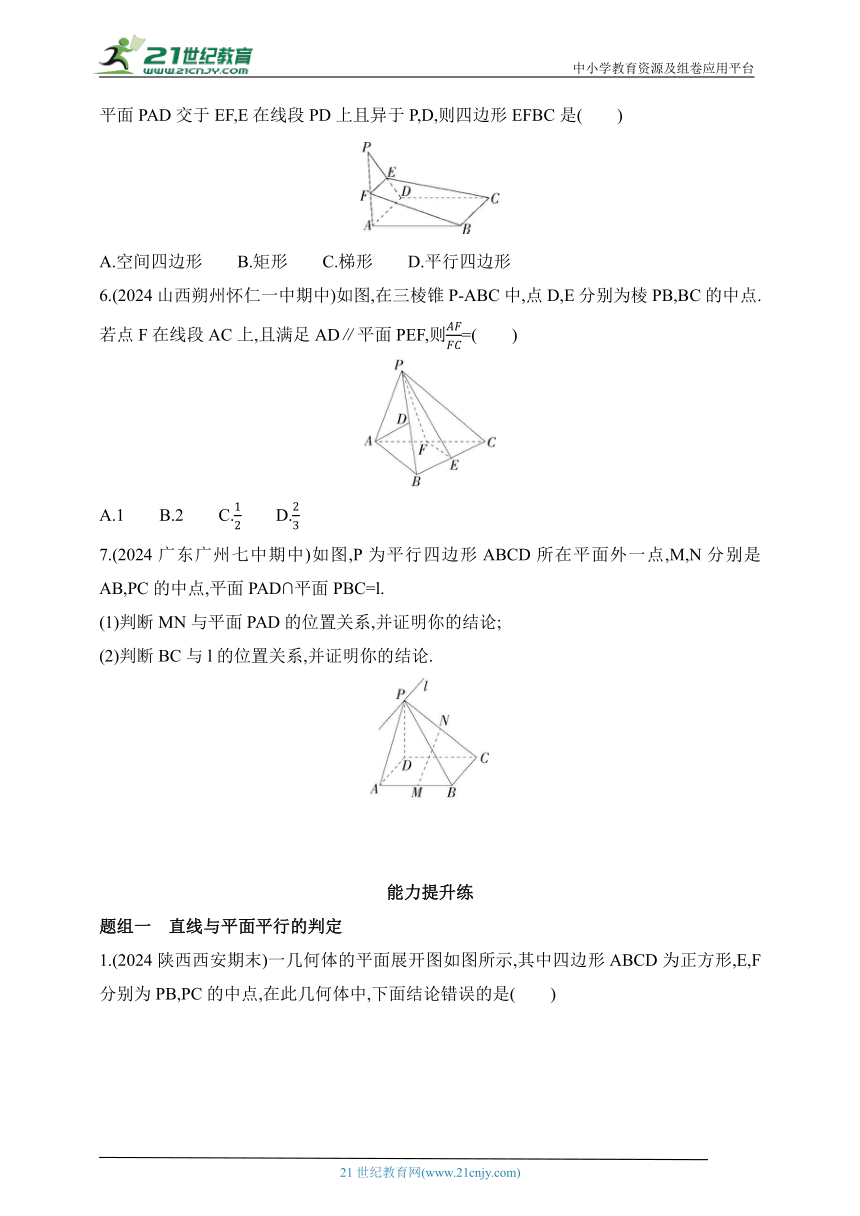
5.(2024陕西西安中学月考)如图,P为平行四边形ABCD所在平面外一点,过BC的平面与平面PAD交于EF,E在线段PD上且异于P,D,则四边形EFBC是( )
A.空间四边形 B.矩形 C.梯形 D.平行四边形
6.(2024山西朔州怀仁一中期中)如图,在三棱锥P-ABC中,点D,E分别为棱PB,BC的中点.若点F在线段AC上,且满足AD∥平面PEF,则=( )
A.1 B.2 C. D.
7.(2024广东广州七中期中)如图,P为平行四边形ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PAD∩平面PBC=l.
(1)判断MN与平面PAD的位置关系,并证明你的结论;
(2)判断BC与l的位置关系,并证明你的结论.
能力提升练
题组一 直线与平面平行的判定
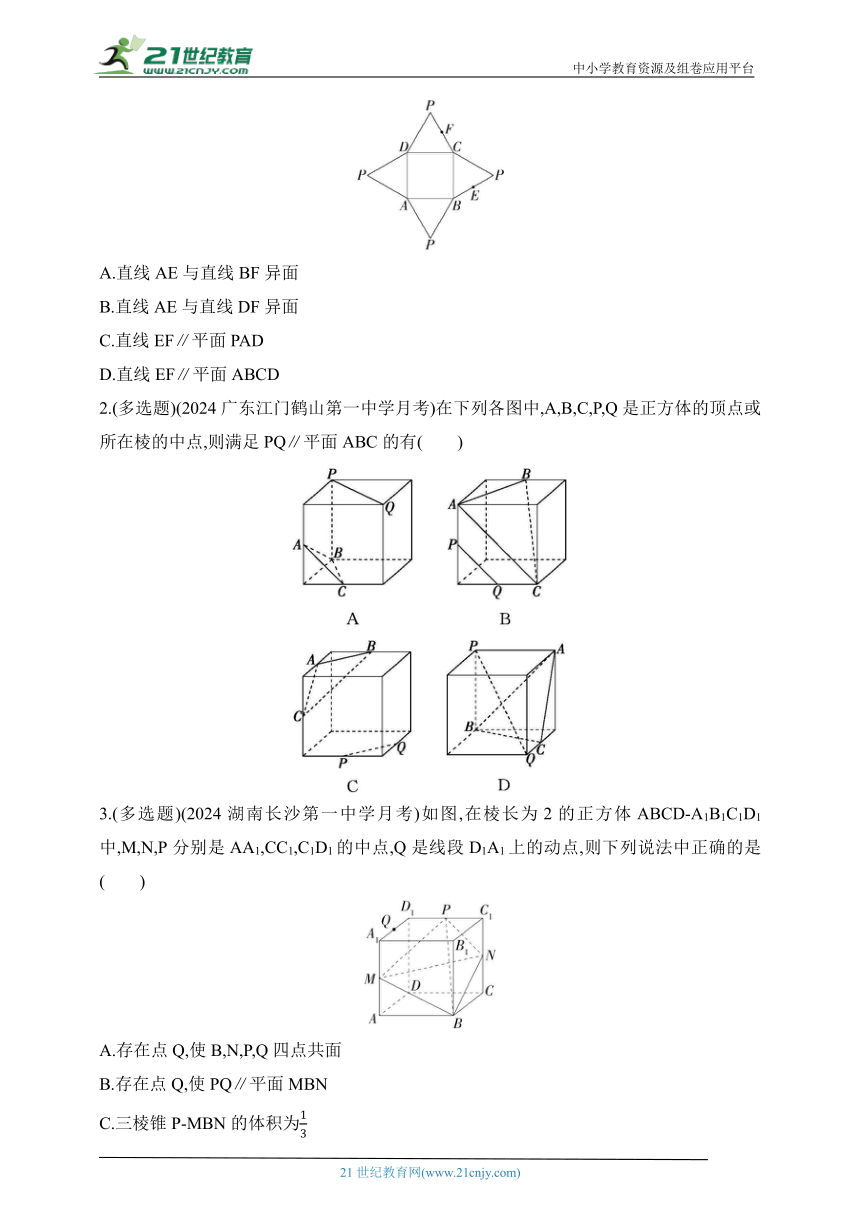
1.(2024陕西西安期末)一几何体的平面展开图如图所示,其中四边形ABCD为正方形,E,F分别为PB,PC的中点,在此几何体中,下面结论错误的是( )
A.直线AE与直线BF异面
B.直线AE与直线DF异面
C.直线EF∥平面PAD
D.直线EF∥平面ABCD
2.(多选题)(2024广东江门鹤山第一中学月考)在下列各图中,A,B,C,P,Q是正方体的顶点或所在棱的中点,则满足PQ∥平面ABC的有( )
3.(多选题)(2024湖南长沙第一中学月考)如图,在棱长为2的正方体ABCD-A1B1C1D1中,M,N,P分别是AA1,CC1,C1D1的中点,Q是线段D1A1上的动点,则下列说法中正确的是( )
A.存在点Q,使B,N,P,Q四点共面
B.存在点Q,使PQ∥平面MBN
C.三棱锥P-MBN的体积为
D.经过C,M,B,N四点的球的表面积为
4.如图,四棱锥P-ABCD的底面ABCD为平行四边形,F,G分别为PB,AD的中点.
(1)证明:AF∥平面PCG;
(2)在线段BD上是否存在一点N,使得FN∥平面PCG,并证明你的结论.
题组二 直线与平面平行的性质定理
5.(2024广东四校联考)如图,已知圆锥的顶点为S,AB为底面圆的直径,M,C为底面圆周上的点,并将弧AB三等分,过AC作平面α,使SB∥平面α,设α与SM交于点N,则的值为( )
A. B. C. D.
6.(多选题)(2024浙江浙南名校联盟期中)如图,四棱锥P-ABCD的底面是平行四边形,E,F分别是棱PD,PA的中点,下列说法正确的有( )
A.多面体ABFDCE是三棱柱
B.直线BF与PC是异面直线
C.平面PAD与平面PBC的交线平行于EF
D.四棱锥P-ABCD和四棱锥P-BCEF的体积之比为8∶3
7.(2024上海虹口高级中学期末)在棱长为1的正方体ABCD-A1B1C1D1中,点P1,P2分别是线段AB,BD1(不包括端点)上的动点,且P1P2∥平面A1ADD1,则四面体P1-P2AB1的体积的最大值是 .
8.(2024福建厦门外国语学校月考)如图所示的是一块正四棱锥木料,侧棱长和底面边长均为13,M为侧棱PA上的点.
(1)若PM∶MA=1∶1,要经过点M和棱BC将木料锯开,在木料表面应该怎样画线 (请写出必要的作图说明)
(2)若PM∶MA=5∶8,在线段BD上是否存在一点N,使直线MN∥平面PBC 如果存在,求出的值以及线段MN的长;如果不存在,请说明理由.
9.(2023黑龙江鹤岗第一中学期中)如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,E为棱PC的中点,平面ABE与棱PD交于点F.
(1)求证:PA∥平面BDE;
(2)求证:F为PD的中点;
(3)在棱AB上是否存在点N,使得FN∥平面BDE 若存在,求出的值;若不存在,请说明理由.
答案与分层梯度式解析
8.5.2 直线与平面平行
基础过关练
1.ABC 2.AC 5.C 6.C
1.ABC 对于A,a∥α或a α,故A中命题错误;
对于B,a∥α,所以a与α没有公共点,又b α,所以a与b没有公共点,所以a与b可能平行也可能异面,故B中命题错误;
对于C,b∥α或b α,故C中命题错误;
对于D,由线面平行的判定定理知D中命题正确.
故选ABC.
2.AC 由题意知O是BD的中点,又M为PB的中点,
∴OM∥PD,∵OM 平面PDA,PD 平面PDA,∴OM∥平面PDA,故A,C正确;OM与平面PAC有公共点O,与平面PBA有公共点M,故OM与平面PAC,平面PBA都不平行,故B,D错误.故选AC.
3.答案 平行;
解析 在△AB1C1中,D,E分别为B1C1和AB1的中点,所以ED∥AC1,
因为DE 平面A1ACC1,AC1 平面A1ACC1,所以DE∥平面A1ACC1.
因为△A1B1C1是边长为1的正三角形,
所以=×1×1×sin 60°=,
因为ABC-A1B1C1为直三棱柱,所以==·AA1=××1=.
4.证明 证法一:如图所示,作ME∥BC,交BB1于点E,作NF∥AD,交AB于点F,连接EF,
则=,=.
易知B1C=BD,又CM=DN,∴B1M=BN.
∴==.
又BC=AD,∴ME=NF.
∵ME∥BC,NF∥AD,AD∥BC,∴ME∥NF,
∴四边形MNFE为平行四边形,∴MN∥EF.
又MN 平面ABB1A1,EF 平面ABB1A1,
∴MN∥平面ABB1A1.
证法二:如图所示,连接CN并延长,交BA的延长线于点P,连接B1P.
易知△DNC∽△BNP,∴=.
∵CM=DN,B1C=BD,∴B1M=BN,
∴==,∴MN∥B1P.
又MN 平面ABB1A1,B1P 平面ABB1A1,
∴MN∥平面ABB1A1.
技巧点拨 判定线面平行,应遵循“先找后作”的原则,即先在平面内找已知直线的平行线,若找不到再作辅助线.
5.C 因为BC∥AD,AD 平面PAD,BC 平面PAD,
所以BC∥平面PAD,
因为BC 平面EFBC,平面EFBC∩平面PAD=EF,
所以BC∥EF,则EF∥AD,由题意知EF因为BC=AD,所以EF所以四边形EFBC为梯形,故选C.
6.C 如图,连接CD,交PE于点G,连接FG,
因为AD∥平面PEF,AD 平面ADC,平面ADC∩平面PEF=FG,所以AD∥FG,所以=.
因为点D,E分别为PB,BC的中点,所以G是△PBC的重心,所以=,即=.
7.解析 (1)MN∥平面PAD,证明如下:
取PD的中点E,连接AE,NE,
因为N,E分别为PC,PD的中点,
所以NE∥DC,且NE=DC,
因为M为AB的中点,AB∥DC,AB=DC,所以AM∥DC,且AM=DC,所以AM∥NE,且AM=NE,
所以四边形AMNE为平行四边形,则AE∥MN,
又AE 平面PAD,MN 平面PAD,
所以MN∥平面PAD.
(2)BC∥l,证明如下:
因为AD∥BC,AD 平面PAD,BC 平面PAD,
所以BC∥平面PAD,
又BC 平面PBC,且平面PAD∩平面PBC=l,
所以根据线面平行的性质定理可得BC∥l.
解题技法 证明线线平行的常用方法:(1)基本事实4;(2)三角形、梯形中位线定理;(3)平行四边形的性质;(4)平行线分线段成比例;(5)线面平行的性质定理.
能力提升练
1.B 2.BD 3.ABC 5.C 6.BCD
1.B 由题意知,该几何体是底面为正方形的四棱锥,如图所示,连接AE,EF,BF,DF,
易得EF∥BC,BC∥AD,则EF∥AD,故EF,AD共面,则AE,DF共面,故B中结论错误;
因为F∈平面AEFD,B 平面AEFD,F不在直线AE上,所以直线AE与直线BF异面,故A中结论正确;
由EF∥AD,EF 平面PAD,AD 平面PAD,得直线EF∥平面PAD,故C中结论正确;
由EF∥AD,EF 平面ABCD,AD 平面ABCD,得直线EF∥平面ABCD,故D中结论正确.
故选B.
2.BD 对于A,如图(1),连接BD,则BD∥PQ,
又BD∩平面ABC=B,所以PQ与平面ABC不平行,故A不符合题意;
对于B,易得PQ∥AC,又PQ 平面ABC,AC 平面ABC,所以PQ∥平面ABC,故B符合题意;
对于C,如图(2),取FN的中点D,连接EF,MN,CD,BD,DQ,CP,
则AB∥EF,PQ∥MN,EF∥MN∥CD,故AB∥CD∥PQ,则A,B,C,D四点共面,易得AC∥DQ,又D∈平面ABDC,所以DQ 平面ABDC,同理可得CP 平面ABDC,所以A,B,C,D,P,Q六点共面(易错点:虽然PQ∥AB,但是PQ 平面ABC),故C不符合题意;
对于D,如图(3),连接PD,交AB于点O,连接OC,
则O为PD的中点,
又C为DQ的中点,所以OC∥PQ,
因为PQ 平面ABC,OC 平面ABC,所以PQ∥平面ABC,故D符合题意.
故选BD.
3.ABC 对于A,连接A1B,CD1,因为N,P分别是CC1,C1D1的中点,所以PN∥CD1.
易知CD1∥A1B,所以A1B∥PN,所以A1,B,N,P四点共面,故当Q与A1重合时,B,N,P,Q四点共面,故A正确.
对于B,连接PQ,A1C1,当Q是D1A1的中点时,PQ∥A1C1,又A1C1∥MN,所以PQ∥MN,因为PQ 平面BMN,MN 平面BMN,所以PQ∥平面BMN,故B正确.
对于C,连接D1M,D1N,D1B,易知D1M∥BN,则VP-MBN=VM-PBN===××1×1×2=,故C正确.
对于D,分别取BB1,DD1的中点E,F,连接ME,EN,NF,MF,
则经过C,M,B,N四点的球即为长方体MADF-EBCN的外接球,设球的直径为2R,则(2R)2=AB2+BC2+CN2=4+4+1=9(长方体的体对角线长为外接球的直径),
所以经过C,M,B,N四点的球的表面积为4πR2=9π,故D错误.
故选ABC.
4.解析 (1)证明:取PC的中点H,连接GH,FH,
在△PBC中,H,F分别为PC,PB的中点,
∴FH∥BC,且FH=BC.
∵AD BC,G为AD的中点,
∴AG∥BC,且AG=BC,∴AG FH,
∴四边形AGHF为平行四边形,∴AF∥GH.
又GH 平面PCG,AF 平面PCG,∴AF∥平面PCG.
(2)存在,证明如下:
连接BD,设BD∩CG=O,取OB的中点K,连接OP,FK.
在△POB中,F,K分别为PB,OB的中点,
∴FK∥OP,
又OP 平面PCG,FK 平面PCG,
∴FK∥平面PCG.
易知△DOG∽△BOC,∴==2,
∴BO=2DO,又BO=2KB,
∴K为BD上靠近点B的三等分点.
∴N在点K处时满足FN∥平面PCG,
即线段BD上存在满足条件的点N,且点N为线段BD上靠近点B的三等分点.
5.C 如图,连接MB,交AC于点D,连接ND,NA,NC,MC,BC,则平面NAC即为平面α.
因为SB∥平面α,平面SMB∩平面α=DN,SB 平面SMB,所以SB∥DN.
因为AB为底面圆的直径,点M,C将弧AB三等分,
所以∠ABM=∠MBC=∠BMC=∠BAC=30°,MC=BC=AB,所以MC∥AB,所以==,
又因为SB∥DN,所以==,所以=.故选C.
方法技巧 利用线面平行的性质定理解决计算问题的三个关键点:(1)根据已知线面平行关系推出线线平行关系;(2)利用三角形中位线定理、平行线分线段成比例等推出有关线段的关系;(3)利用所得关系计算求值.
6.BCD 对于A,由AF∩DE=P,知平面ABF与平面DCE不平行,则多面体ABFDCE中不存在互相平行的两个面,则该多面体不是三棱柱,A错误;
对于B,由E,F分别是PD,PA的中点,得EF∥AD,又AD∥BC,∴EF∥BC,故EF,BC共面,∵BF 平面BCEF,C∈平面BCEF,P 平面BCEF,C BF,∴直线BF与PC是异面直线,B正确;
对于C,设平面PBC∩平面PAD=l,由AD∥BC,BC 平面PBC,AD 平面PBC,得AD∥平面PBC,又AD 平面PAD,平面PBC∩平面PAD=l,∴l∥AD,又AD∥EF,∴l∥EF,C正确;
对于D,连接AC,CF,设四棱锥P-ABCD的体积为V,由E,F分别是棱PD,PA的中点,得VP-BCF=VB-PCF=VB-PCA=VP-ABC=V,VP-CEF=VC-PEF=VC-PDA=VP-ADC=V,
因此VP-BCEF=VP-BCF+VP-CEF=V,D正确.故选BCD.
7.答案
解析 如图,连接AD1,∵P1P2∥平面A1ADD1,平面ABD1∩平面A1ADD1=AD1,P1P2 平面ABD1,∴由线面平行的性质定理知P1P2∥AD1,
∴△P1P2B∽△AD1B,则==,
设P1B=x,x∈(0,1),P2到平面AA1B1B的距离为h,则=,所以h=x,
所以==××(1-x)×1×x=(x-x2)=-+,
当x=时,四面体P1-P2AB1的体积取得最大值,为.
8.解析 (1)因为PM∶MA=1∶1,所以M为PA的中点,作MG∥AD,交PD于G,则G为PD的中点,
连接MB,GC,由题意知四边形ABCD为正方形,所以BC∥AD,故GM∥BC,即B,M,G,C共面,
故要经过点M和棱BC将木料锯开,在木料表面沿线段BM,MG,GC画线即可.
(2)假设在线段BD上存在一点N,使直线MN∥平面PBC,如图,连接AN并延长,交BC于E,连接PE,
因为MN∥平面PBC,MN 平面PAE,平面PAE∩平面PBC=PE,
所以MN∥PE,则==,
由题意知BC∥AD,所以==,
故在线段BD上存在一点N,使直线MN∥平面PBC,此时=.
由BC∥AD,得==,又AD=13,所以BE=,
在△PBE中,由余弦定理得PE2=PB2+BE2-2PB·BEcos 60°=132+-2×13××=,
所以PE=,因为MN∥PE,PM∶MA=5∶8,
所以==,则MN=×=7.
方法技巧 解决探索性问题的基本方法是假设结论成立或对象存在,然后在这个前提下进行逻辑推理,若能推导出正确的结果,则说明假设成立,即存在,并可进一步证明,否则不成立,即不存在.
9.解析 (1)证明:连接AC,交BD于点G,连接GE,
因为四边形ABCD为平行四边形,
所以G为AC的中点,
又E为PC的中点,所以GE∥PA.
又GE 平面BDE,PA 平面BDE,
所以PA∥平面BDE.
(2)证明:因为CD∥AB,AB 平面ABEF,CD 平面ABEF,所以CD∥平面ABEF,
又CD 平面PDC,平面PDC∩平面ABEF=EF,所以CD∥EF,又E为PC的中点,所以F为PD的中点.
(3)取AB的中点H,连接FH,
则BH=AB=CD,且BH∥CD,
由(2)知CD∥EF,且EF=CD,
所以BH EF,所以四边形BHFE为平行四边形,
所以FH∥BE,而BE 平面BDE,FH 平面BDE,
所以FH∥平面BDE,故所求点N即为点H,
故在棱AB上存在点N,使得FN∥平面BDE,且=1.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教A版高中数学必修第二册
8.5.2 直线与平面平行
基础过关练
题组一 直线与平面平行的判定
1.(多选题)(2024陕西咸阳期中)已知a,b是不同的直线,α是平面,下列命题错误的是( )
A.a∥b,b α a∥α
B.a∥α,b α a∥b
C.a∥α,a∥b b∥α
D.a α,a∥b,b α a∥α
2.(多选题)(2024广东湛江雷州第二中学月考)如图所示,P为矩形ABCD所在平面外一点,矩形对角线的交点为O,M为PB的中点,则以下结论正确的是( )
OM∥PD B.OM∥平面PAC
C.OM∥平面PDA D.OM∥平面PBA
3.(2024河北沧州期中)如图,直三棱柱ABC-A1B1C1的所有棱长都为1,D,E分别为B1C1和AB1的中点,则DE与平面A1ACC1的位置关系是 ,三棱锥C1-AA1B1的体积为 .
4.如图所示,在正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN,求证:MN∥平面ABB1A1.
题组二 直线与平面平行的性质定理
5.(2024陕西西安中学月考)如图,P为平行四边形ABCD所在平面外一点,过BC的平面与平面PAD交于EF,E在线段PD上且异于P,D,则四边形EFBC是( )
A.空间四边形 B.矩形 C.梯形 D.平行四边形
6.(2024山西朔州怀仁一中期中)如图,在三棱锥P-ABC中,点D,E分别为棱PB,BC的中点.若点F在线段AC上,且满足AD∥平面PEF,则=( )
A.1 B.2 C. D.
7.(2024广东广州七中期中)如图,P为平行四边形ABCD所在平面外一点,M,N分别是AB,PC的中点,平面PAD∩平面PBC=l.
(1)判断MN与平面PAD的位置关系,并证明你的结论;
(2)判断BC与l的位置关系,并证明你的结论.
能力提升练
题组一 直线与平面平行的判定
1.(2024陕西西安期末)一几何体的平面展开图如图所示,其中四边形ABCD为正方形,E,F分别为PB,PC的中点,在此几何体中,下面结论错误的是( )
A.直线AE与直线BF异面
B.直线AE与直线DF异面
C.直线EF∥平面PAD
D.直线EF∥平面ABCD
2.(多选题)(2024广东江门鹤山第一中学月考)在下列各图中,A,B,C,P,Q是正方体的顶点或所在棱的中点,则满足PQ∥平面ABC的有( )
3.(多选题)(2024湖南长沙第一中学月考)如图,在棱长为2的正方体ABCD-A1B1C1D1中,M,N,P分别是AA1,CC1,C1D1的中点,Q是线段D1A1上的动点,则下列说法中正确的是( )
A.存在点Q,使B,N,P,Q四点共面
B.存在点Q,使PQ∥平面MBN
C.三棱锥P-MBN的体积为
D.经过C,M,B,N四点的球的表面积为
4.如图,四棱锥P-ABCD的底面ABCD为平行四边形,F,G分别为PB,AD的中点.
(1)证明:AF∥平面PCG;
(2)在线段BD上是否存在一点N,使得FN∥平面PCG,并证明你的结论.
题组二 直线与平面平行的性质定理
5.(2024广东四校联考)如图,已知圆锥的顶点为S,AB为底面圆的直径,M,C为底面圆周上的点,并将弧AB三等分,过AC作平面α,使SB∥平面α,设α与SM交于点N,则的值为( )
A. B. C. D.
6.(多选题)(2024浙江浙南名校联盟期中)如图,四棱锥P-ABCD的底面是平行四边形,E,F分别是棱PD,PA的中点,下列说法正确的有( )
A.多面体ABFDCE是三棱柱
B.直线BF与PC是异面直线
C.平面PAD与平面PBC的交线平行于EF
D.四棱锥P-ABCD和四棱锥P-BCEF的体积之比为8∶3
7.(2024上海虹口高级中学期末)在棱长为1的正方体ABCD-A1B1C1D1中,点P1,P2分别是线段AB,BD1(不包括端点)上的动点,且P1P2∥平面A1ADD1,则四面体P1-P2AB1的体积的最大值是 .
8.(2024福建厦门外国语学校月考)如图所示的是一块正四棱锥木料,侧棱长和底面边长均为13,M为侧棱PA上的点.
(1)若PM∶MA=1∶1,要经过点M和棱BC将木料锯开,在木料表面应该怎样画线 (请写出必要的作图说明)
(2)若PM∶MA=5∶8,在线段BD上是否存在一点N,使直线MN∥平面PBC 如果存在,求出的值以及线段MN的长;如果不存在,请说明理由.
9.(2023黑龙江鹤岗第一中学期中)如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,E为棱PC的中点,平面ABE与棱PD交于点F.
(1)求证:PA∥平面BDE;
(2)求证:F为PD的中点;
(3)在棱AB上是否存在点N,使得FN∥平面BDE 若存在,求出的值;若不存在,请说明理由.
答案与分层梯度式解析
8.5.2 直线与平面平行
基础过关练
1.ABC 2.AC 5.C 6.C
1.ABC 对于A,a∥α或a α,故A中命题错误;
对于B,a∥α,所以a与α没有公共点,又b α,所以a与b没有公共点,所以a与b可能平行也可能异面,故B中命题错误;
对于C,b∥α或b α,故C中命题错误;
对于D,由线面平行的判定定理知D中命题正确.
故选ABC.
2.AC 由题意知O是BD的中点,又M为PB的中点,
∴OM∥PD,∵OM 平面PDA,PD 平面PDA,∴OM∥平面PDA,故A,C正确;OM与平面PAC有公共点O,与平面PBA有公共点M,故OM与平面PAC,平面PBA都不平行,故B,D错误.故选AC.
3.答案 平行;
解析 在△AB1C1中,D,E分别为B1C1和AB1的中点,所以ED∥AC1,
因为DE 平面A1ACC1,AC1 平面A1ACC1,所以DE∥平面A1ACC1.
因为△A1B1C1是边长为1的正三角形,
所以=×1×1×sin 60°=,
因为ABC-A1B1C1为直三棱柱,所以==·AA1=××1=.
4.证明 证法一:如图所示,作ME∥BC,交BB1于点E,作NF∥AD,交AB于点F,连接EF,
则=,=.
易知B1C=BD,又CM=DN,∴B1M=BN.
∴==.
又BC=AD,∴ME=NF.
∵ME∥BC,NF∥AD,AD∥BC,∴ME∥NF,
∴四边形MNFE为平行四边形,∴MN∥EF.
又MN 平面ABB1A1,EF 平面ABB1A1,
∴MN∥平面ABB1A1.
证法二:如图所示,连接CN并延长,交BA的延长线于点P,连接B1P.
易知△DNC∽△BNP,∴=.
∵CM=DN,B1C=BD,∴B1M=BN,
∴==,∴MN∥B1P.
又MN 平面ABB1A1,B1P 平面ABB1A1,
∴MN∥平面ABB1A1.
技巧点拨 判定线面平行,应遵循“先找后作”的原则,即先在平面内找已知直线的平行线,若找不到再作辅助线.
5.C 因为BC∥AD,AD 平面PAD,BC 平面PAD,
所以BC∥平面PAD,
因为BC 平面EFBC,平面EFBC∩平面PAD=EF,
所以BC∥EF,则EF∥AD,由题意知EF
6.C 如图,连接CD,交PE于点G,连接FG,
因为AD∥平面PEF,AD 平面ADC,平面ADC∩平面PEF=FG,所以AD∥FG,所以=.
因为点D,E分别为PB,BC的中点,所以G是△PBC的重心,所以=,即=.
7.解析 (1)MN∥平面PAD,证明如下:
取PD的中点E,连接AE,NE,
因为N,E分别为PC,PD的中点,
所以NE∥DC,且NE=DC,
因为M为AB的中点,AB∥DC,AB=DC,所以AM∥DC,且AM=DC,所以AM∥NE,且AM=NE,
所以四边形AMNE为平行四边形,则AE∥MN,
又AE 平面PAD,MN 平面PAD,
所以MN∥平面PAD.
(2)BC∥l,证明如下:
因为AD∥BC,AD 平面PAD,BC 平面PAD,
所以BC∥平面PAD,
又BC 平面PBC,且平面PAD∩平面PBC=l,
所以根据线面平行的性质定理可得BC∥l.
解题技法 证明线线平行的常用方法:(1)基本事实4;(2)三角形、梯形中位线定理;(3)平行四边形的性质;(4)平行线分线段成比例;(5)线面平行的性质定理.
能力提升练
1.B 2.BD 3.ABC 5.C 6.BCD
1.B 由题意知,该几何体是底面为正方形的四棱锥,如图所示,连接AE,EF,BF,DF,
易得EF∥BC,BC∥AD,则EF∥AD,故EF,AD共面,则AE,DF共面,故B中结论错误;
因为F∈平面AEFD,B 平面AEFD,F不在直线AE上,所以直线AE与直线BF异面,故A中结论正确;
由EF∥AD,EF 平面PAD,AD 平面PAD,得直线EF∥平面PAD,故C中结论正确;
由EF∥AD,EF 平面ABCD,AD 平面ABCD,得直线EF∥平面ABCD,故D中结论正确.
故选B.
2.BD 对于A,如图(1),连接BD,则BD∥PQ,
又BD∩平面ABC=B,所以PQ与平面ABC不平行,故A不符合题意;
对于B,易得PQ∥AC,又PQ 平面ABC,AC 平面ABC,所以PQ∥平面ABC,故B符合题意;
对于C,如图(2),取FN的中点D,连接EF,MN,CD,BD,DQ,CP,
则AB∥EF,PQ∥MN,EF∥MN∥CD,故AB∥CD∥PQ,则A,B,C,D四点共面,易得AC∥DQ,又D∈平面ABDC,所以DQ 平面ABDC,同理可得CP 平面ABDC,所以A,B,C,D,P,Q六点共面(易错点:虽然PQ∥AB,但是PQ 平面ABC),故C不符合题意;
对于D,如图(3),连接PD,交AB于点O,连接OC,
则O为PD的中点,
又C为DQ的中点,所以OC∥PQ,
因为PQ 平面ABC,OC 平面ABC,所以PQ∥平面ABC,故D符合题意.
故选BD.
3.ABC 对于A,连接A1B,CD1,因为N,P分别是CC1,C1D1的中点,所以PN∥CD1.
易知CD1∥A1B,所以A1B∥PN,所以A1,B,N,P四点共面,故当Q与A1重合时,B,N,P,Q四点共面,故A正确.
对于B,连接PQ,A1C1,当Q是D1A1的中点时,PQ∥A1C1,又A1C1∥MN,所以PQ∥MN,因为PQ 平面BMN,MN 平面BMN,所以PQ∥平面BMN,故B正确.
对于C,连接D1M,D1N,D1B,易知D1M∥BN,则VP-MBN=VM-PBN===××1×1×2=,故C正确.
对于D,分别取BB1,DD1的中点E,F,连接ME,EN,NF,MF,
则经过C,M,B,N四点的球即为长方体MADF-EBCN的外接球,设球的直径为2R,则(2R)2=AB2+BC2+CN2=4+4+1=9(长方体的体对角线长为外接球的直径),
所以经过C,M,B,N四点的球的表面积为4πR2=9π,故D错误.
故选ABC.
4.解析 (1)证明:取PC的中点H,连接GH,FH,
在△PBC中,H,F分别为PC,PB的中点,
∴FH∥BC,且FH=BC.
∵AD BC,G为AD的中点,
∴AG∥BC,且AG=BC,∴AG FH,
∴四边形AGHF为平行四边形,∴AF∥GH.
又GH 平面PCG,AF 平面PCG,∴AF∥平面PCG.
(2)存在,证明如下:
连接BD,设BD∩CG=O,取OB的中点K,连接OP,FK.
在△POB中,F,K分别为PB,OB的中点,
∴FK∥OP,
又OP 平面PCG,FK 平面PCG,
∴FK∥平面PCG.
易知△DOG∽△BOC,∴==2,
∴BO=2DO,又BO=2KB,
∴K为BD上靠近点B的三等分点.
∴N在点K处时满足FN∥平面PCG,
即线段BD上存在满足条件的点N,且点N为线段BD上靠近点B的三等分点.
5.C 如图,连接MB,交AC于点D,连接ND,NA,NC,MC,BC,则平面NAC即为平面α.
因为SB∥平面α,平面SMB∩平面α=DN,SB 平面SMB,所以SB∥DN.
因为AB为底面圆的直径,点M,C将弧AB三等分,
所以∠ABM=∠MBC=∠BMC=∠BAC=30°,MC=BC=AB,所以MC∥AB,所以==,
又因为SB∥DN,所以==,所以=.故选C.
方法技巧 利用线面平行的性质定理解决计算问题的三个关键点:(1)根据已知线面平行关系推出线线平行关系;(2)利用三角形中位线定理、平行线分线段成比例等推出有关线段的关系;(3)利用所得关系计算求值.
6.BCD 对于A,由AF∩DE=P,知平面ABF与平面DCE不平行,则多面体ABFDCE中不存在互相平行的两个面,则该多面体不是三棱柱,A错误;
对于B,由E,F分别是PD,PA的中点,得EF∥AD,又AD∥BC,∴EF∥BC,故EF,BC共面,∵BF 平面BCEF,C∈平面BCEF,P 平面BCEF,C BF,∴直线BF与PC是异面直线,B正确;
对于C,设平面PBC∩平面PAD=l,由AD∥BC,BC 平面PBC,AD 平面PBC,得AD∥平面PBC,又AD 平面PAD,平面PBC∩平面PAD=l,∴l∥AD,又AD∥EF,∴l∥EF,C正确;
对于D,连接AC,CF,设四棱锥P-ABCD的体积为V,由E,F分别是棱PD,PA的中点,得VP-BCF=VB-PCF=VB-PCA=VP-ABC=V,VP-CEF=VC-PEF=VC-PDA=VP-ADC=V,
因此VP-BCEF=VP-BCF+VP-CEF=V,D正确.故选BCD.
7.答案
解析 如图,连接AD1,∵P1P2∥平面A1ADD1,平面ABD1∩平面A1ADD1=AD1,P1P2 平面ABD1,∴由线面平行的性质定理知P1P2∥AD1,
∴△P1P2B∽△AD1B,则==,
设P1B=x,x∈(0,1),P2到平面AA1B1B的距离为h,则=,所以h=x,
所以==××(1-x)×1×x=(x-x2)=-+,
当x=时,四面体P1-P2AB1的体积取得最大值,为.
8.解析 (1)因为PM∶MA=1∶1,所以M为PA的中点,作MG∥AD,交PD于G,则G为PD的中点,
连接MB,GC,由题意知四边形ABCD为正方形,所以BC∥AD,故GM∥BC,即B,M,G,C共面,
故要经过点M和棱BC将木料锯开,在木料表面沿线段BM,MG,GC画线即可.
(2)假设在线段BD上存在一点N,使直线MN∥平面PBC,如图,连接AN并延长,交BC于E,连接PE,
因为MN∥平面PBC,MN 平面PAE,平面PAE∩平面PBC=PE,
所以MN∥PE,则==,
由题意知BC∥AD,所以==,
故在线段BD上存在一点N,使直线MN∥平面PBC,此时=.
由BC∥AD,得==,又AD=13,所以BE=,
在△PBE中,由余弦定理得PE2=PB2+BE2-2PB·BEcos 60°=132+-2×13××=,
所以PE=,因为MN∥PE,PM∶MA=5∶8,
所以==,则MN=×=7.
方法技巧 解决探索性问题的基本方法是假设结论成立或对象存在,然后在这个前提下进行逻辑推理,若能推导出正确的结果,则说明假设成立,即存在,并可进一步证明,否则不成立,即不存在.
9.解析 (1)证明:连接AC,交BD于点G,连接GE,
因为四边形ABCD为平行四边形,
所以G为AC的中点,
又E为PC的中点,所以GE∥PA.
又GE 平面BDE,PA 平面BDE,
所以PA∥平面BDE.
(2)证明:因为CD∥AB,AB 平面ABEF,CD 平面ABEF,所以CD∥平面ABEF,
又CD 平面PDC,平面PDC∩平面ABEF=EF,所以CD∥EF,又E为PC的中点,所以F为PD的中点.
(3)取AB的中点H,连接FH,
则BH=AB=CD,且BH∥CD,
由(2)知CD∥EF,且EF=CD,
所以BH EF,所以四边形BHFE为平行四边形,
所以FH∥BE,而BE 平面BDE,FH 平面BDE,
所以FH∥平面BDE,故所求点N即为点H,
故在棱AB上存在点N,使得FN∥平面BDE,且=1.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
