2025人教A版高中数学必修第二册强化练习题--8.6.1 直线与直线垂直
文档属性
| 名称 | 2025人教A版高中数学必修第二册强化练习题--8.6.1 直线与直线垂直 |

|
|
| 格式 | docx | ||
| 文件大小 | 474.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025人教A版高中数学必修第二册
8.6 空间直线、平面的垂直
8.6.1 直线与直线垂直
基础过关练
题组一 求异面直线所成的角
1.(2024安徽六安期中)如图,已知正四棱锥P-ABCD的所有棱长均为2,E为棱PA的中点,则异面直线BE与PC所成角的余弦值为( )
A. B. C. D.
2.(2024山东威海模拟)在正方体ABCD-A1B1C1D1中,E,F分别为棱BC,B1C1的中点,若平面DBB1与平面AEF的交线为l,则l与直线AD1所成角的大小为( )
A. B. C. D.
3.(2023浙江绍兴期末)如图,已知正三棱柱ABC-A1B1C1中,AB=4,AA1=3,点M为A1B1的中点,则异面直线AM与B1C所成角的余弦值为 ( )
A. B. C. D.
4.(2024浙江杭州外国语学校期中)在正方体ABCD-A1B1C1D1中,M,N分别是BC1,CD1的中点.
(1)求异面直线CD1与BC1所成的角;
(2)求证:MN∥平面ABCD.
题组二 空间两条直线所成角的应用
5.(多选题)(2024山东德州夏津第一中学月考)已知E,F分别是三棱锥P-ABC的棱PA,BC的中点,且PC=6,AB=8.若异面直线PC与AB所成角的大小为60°,则线段EF的长可能为( )
A. B. C.5 D.
6.在长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,异面直线AB与A1C所成角的大小为,则该长方体的表面积与体积的比值是( )
A. B. C. D.4+
7.(2024广东深圳高级中学期中)如图,已知圆柱O1O2的底面半径和母线长均为1,B,A分别为上、下底面圆周上的点,若异面直线O1B,O2A所成的角为,则AB的长为 .
能力提升练
题组一 求异面直线所成的角
1.(2024浙江杭州第二中学期中)在正四面体S-ABC中,M是SC的中点,N是SB的中点,则异面直线BM与AN所成角的余弦值为( )
A. B. C. D.
2.(2024江苏南通期中)在圆锥PO中,轴截面PAB为等腰直角三角形,M为底面圆O上一点,∠AOM=30°,则异面直线OM与AP所成角的余弦值为( )
A. B. C. D.
3.当动点P在正方体ABCD-A1B1C1D1的棱DC上运动时,异面直线D1P与BC1所成角的取值范围是( )
A. B. C. D.
4.(2024贵州凯里第一中学模拟)平面α过直三棱柱ABC-A1B1C1的顶点B1,平面α∥平面ABC1,平面α∩平面BB1C1C=l,且AA1=AB=BC,AB⊥BC,则A1B与l所成角的正弦值为( )
A. B. C. D.
5.已知正三棱柱ABC-A1B1C1的侧面积为12,当其外接球的表面积取最小值时,异面直线AC1与B1C所成角的余弦值为 .
题组二 异面直线所成角的应用
6.(2024上海青浦高级中学期末)在棱长为1的正方体ABCD-
A1B1C1D1中,P为底面ABCD内(包括边界)的动点,满足直线D1P与CC1所成角的大小为,则线段DP扫过的面积为( )
A. B. C. D.
7.(2024广东阳江期末)在四面体A-BCD中,AB=CD=1,BC=2,且AB⊥BC,CD⊥BC,异面直线AB与CD所成的角为,则该四面体外接球的表面积为 .
8.(2022河南濮阳第一高级中学月考)在四棱柱ABCD-A1B1C1D1中,侧面都是矩形,底面ABCD是菱形且AB=BC=2,∠ABC=120°,若异面直线A1B和AD1所成的角为90°,求AA1的长度.
答案与分层梯度式解析
8.6 空间直线、平面的垂直
8.6.1 直线与直线垂直
基础过关练
1.B 2.C 3.A 5.BD 6.D
1.B 连接AC,取AC的中点O,连接OE,OB,则EO∥PC,EO=PC=1,故异面直线BE与PC所成的角为∠BEO(或其补角),
在△BEO中,EO=1,BO=,BE=,则由余弦定理的推论得cos∠BEO==,
故异面直线BE与PC所成角的余弦值为.
故选B.
解题模板 求异面直线所成角的一般步骤:
(1)作:通过作平行线或平移其中一条直线,构造异面直线所成角或其补角;
(2)证:证明所作的角或其补角为异面直线所成角;
(3)计算:一般在三角形中求角.
2.C 如图,因为E,F分别为棱BC,B1C1的中点,所以BB1∥EF,
因为EF 平面AEF,BB1 平面AEF,所以BB1∥平面AEF,
又平面DBB1∩平面AEF=l,BB1 平面DBB1,所以BB1∥l,
又AA1∥BB1,所以AA1∥l,所以l与直线AD1所成的角为∠A1AD1=.故选C.
3.A 如图所示,取AB的中点N,连接B1N,CN,
因为点M为A1B1的中点,A1B1=AB,所以MB1=AN,又MB1∥AN,所以四边形ANB1M为平行四边形,所以AM∥B1N,
所以异面直线AM与B1C所成的角为∠CB1N(或其补角),设∠CB1N=θ,
在正△ABC中,由AB=4,可得CN=2,
在直角△BNB1中,BB1=3,BN=2,所以B1N==,
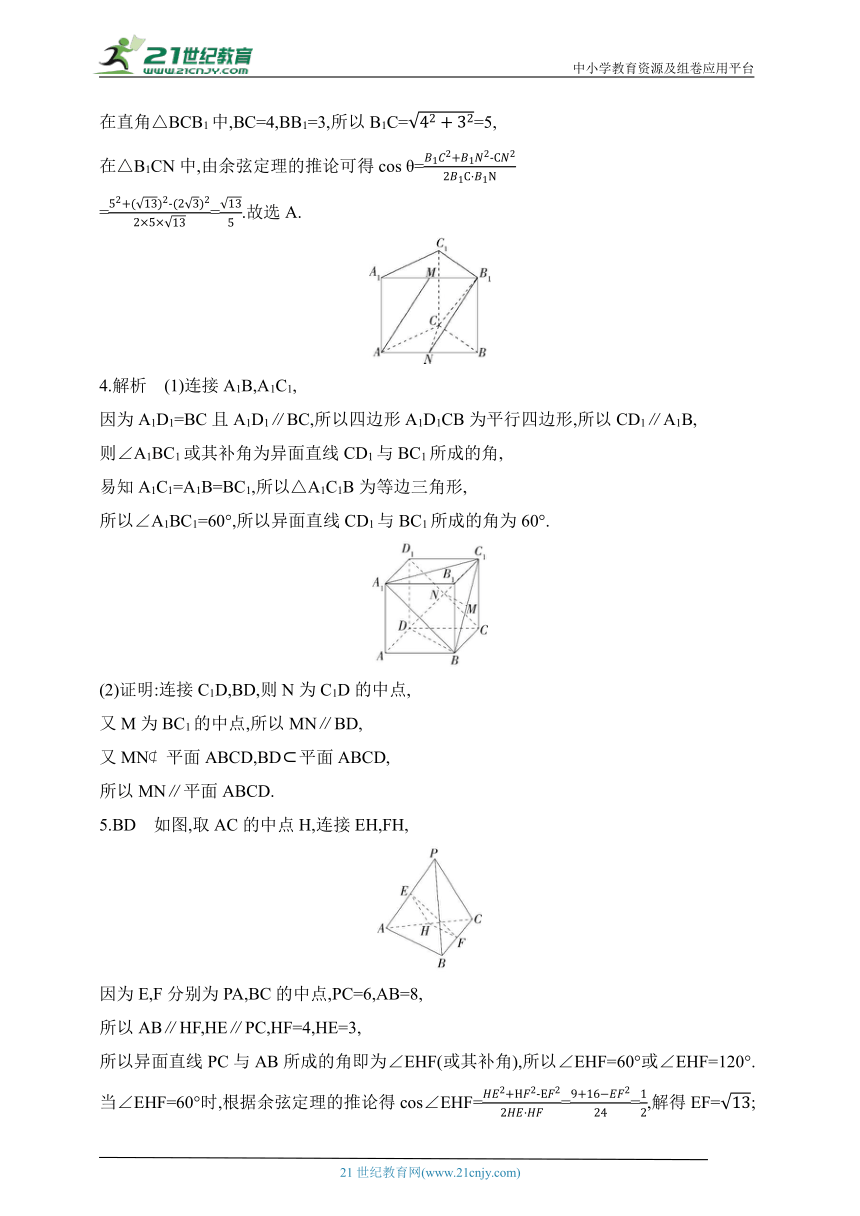
在直角△BCB1中,BC=4,BB1=3,所以B1C==5,
在△B1CN中,由余弦定理的推论可得cos θ=
==.故选A.
4.解析 (1)连接A1B,A1C1,
因为A1D1=BC且A1D1∥BC,所以四边形A1D1CB为平行四边形,所以CD1∥A1B,
则∠A1BC1或其补角为异面直线CD1与BC1所成的角,
易知A1C1=A1B=BC1,所以△A1C1B为等边三角形,
所以∠A1BC1=60°,所以异面直线CD1与BC1所成的角为60°.
(2)证明:连接C1D,BD,则N为C1D的中点,
又M为BC1的中点,所以MN∥BD,
又MN 平面ABCD,BD 平面ABCD,
所以MN∥平面ABCD.
5.BD 如图,取AC的中点H,连接EH,FH,
因为E,F分别为PA,BC的中点,PC=6,AB=8,
所以AB∥HF,HE∥PC,HF=4,HE=3,
所以异面直线PC与AB所成的角即为∠EHF(或其补角),所以∠EHF=60°或∠EHF=120°.
当∠EHF=60°时,根据余弦定理的推论得cos∠EHF===,解得EF=;
当∠EHF=120°时,根据余弦定理的推论得cos∠EHF===-,解得EF=.故选BD.
易错警示 通过立体图形无法直接判断∠EHF是锐角还是钝角,因此∠EHF可能是异面直线所成的角,也可能是其补角,所以需要进行分类讨论.
6.D ∵AB∥DC,∴∠A1CD(或其补角)即为异面直线AB与A1C所成的角,由图可知∠A1CD为锐角,∴∠A1CD=.
设DD1=x,连接A1D,则A1C==,A1D=.
在△A1CD中,cos ==,解得x=(负值舍去),
∴长方体的表面积S=2+4×=2+4,体积V=,
∴该长方体的表面积与体积的比值为=4+.故选D.
7.答案 2或
解析 如图,过点A作AD垂直于上底面于点D,则AD是圆柱的母线,连接DB,DO1,
易知AD∥O1O2,AD=O1O2,
则四边形ADO1O2是平行四边形,∴O1D∥O2A,
∴O2A与O1B所成的角就是∠DO1B或其补角,
∴∠DO1B=或∠DO1B=.
当∠DO1B=时,△DO1B是等边三角形,BD=1,
在Rt△ABD中,AB==;
当∠DO1B=时,在△DO1B中,BD=2×=,
在Rt△ABD中,AB==2.
综上,AB=2或AB=.
能力提升练
1.A 2.A 3.C 4.A 6.A
1.A 取SM的中点E,连接EN,AE,如图,
∵N是SB的中点,∴EN∥MB,EN=MB,
∴∠ANE或其补角即为异面直线BM与AN所成的角.
设正四面体的棱长为4,
∵M是SC的中点,N是SB的中点,△SAB和△SBC均为正三角形,∴BM⊥SC,AN⊥SB,且BM=AN=2,∴EN=,
在△ASE中,由余弦定理得AE2=SA2+SE2-2SA·SE·cos∠ASE=16+1-2×4×1×=13,
在△ANE中,由余弦定理的推论得cos∠ANE===,
∴异面直线BM与AN所成角的余弦值为.故选A.
2.A 如图,过点A作AN∥OM,交圆O于点N,连接ON,PN,
则∠PAN或其补角即为异面直线OM与AP所成的角,
设AO=ON=1,易知∠OAN=∠ONA=∠AOM=30°,则AN=,
因为轴截面PAB为等腰直角三角形,所以PN=PA=,
在△APN中,由余弦定理的推论得cos∠PAN===,
所以异面直线OM与AP所成角的余弦值为.
故选A.
3.C 如图,连接AD1,AP,
易得AD1∥BC1,所以∠AD1P(或其补角)即为异面直线D1P与BC1所成的角.
设正方体的棱长为1,DP=x,x∈[0,1],
在△AD1P中,AD1=,AP=D1P=,
故cos∠AD1P==,
∵x∈[0,1],∴cos∠AD1P=∈,
又∠AD1P是△AD1P的内角,
∴∠AD1P∈,故选C.
4.A 如图所示,将直三棱柱ABC-A1B1C1补成直三棱柱ABC-A2B2C2,且AA1=A1A2,连接B1C2,A1C2,
则B1C2∥BC1,A1B1∥AB,
因为B1C2 平面ABC1,BC1 平面ABC1,所以B1C2∥平面ABC1,因为A1B1 平面ABC1,AB 平面ABC1,
所以A1B1∥平面ABC1,
又因为B1C2∩A1B1=B1,且B1C2,A1B1 平面A1B1C2,
所以平面A1B1C2∥平面ABC1,又B1∈平面A1B1C2,所以平面A1B1C2即为平面α,所以l即为直线B1C2,
因为B1C2∥BC1,所以A1B与l所成的角为∠A1BC1(或其补角),
由AA1=AB=BC,AB⊥BC,可得A1C1=BC1=BA1,
所以△A1BC1为等边三角形,所以∠A1BC1=60°,所以sin∠A1BC1=,即A1B与l所成角的正弦值为.
故选A.
小题速解 因为平面α∥平面ABC1,平面α∩平面BB1C1C=l,平面ABC1∩平面BB1C1C=BC1,
所以l∥BC1,则A1B与l所成的角为∠A1BC1(或其补角),
下同解析.
5.答案
解析 设正三棱柱的底面边长为a,高为h,外接球的半径为R,由题意知3ah=12,即ah=4,
易得△ABC外接圆的半径r==,
则R2=r2+=+≥=,当且仅当a=h时取等号,此时外接球的表面积最小.
将三棱柱补成一个四棱柱,如图,连接DB1,DC,
则AC1∥DB1,∴∠DB1C(或其补角)为异面直线AC1与B1C所成的角,易得B1C=DB1=,DC=a,
∴cos∠DB1C==.
解题技法 补形平移是常用的一种作平行线的方法,一般是补一个相同形状的几何体,构成一个特殊的几何体,方便作平行线,如此题将三棱柱补成一个四棱柱.
6.A 因为DD1∥CC1,所以直线D1P与CC1所成的角即为DD1与D1P所成的角,
易知DD1⊥PD,所以DD1与D1P所成的角为∠DD1P,即∠DD1P=,故tan∠DD1P==,即DP=,
所以点P的轨迹是以D为圆心,为半径的圆的四分之一,
故线段DP扫过的面积为π×=.
故选A.
7.答案 或8π
解析 由题意,可以将四面体A-BCD补成一个直三棱柱,如图所示.
∵CD∥BE,∴直线AB与CD所成的角为∠ABE或其补角,
∵异面直线AB与CD所成的角为,
∴∠ABE=或∠ABE=.
设△ABE外接圆的半径为r,当∠ABE=时,AE=BE=AB=1,则2r=,解得r=;
当∠ABE=时,AE=,
则2r=,解得r=1.
设四面体外接球的半径为R,
则R==,∴R=或R=,
则外接球的表面积为或8π.
8.解析 如图,连接AC,CD1,
在四棱柱ABCD-A1B1C1D1中,A1D1∥BC且A1D1=BC,
所以四边形A1BCD1为平行四边形,所以A1B∥CD1,
所以异面直线A1B和AD1所成的角为∠AD1C,故∠AD1C=90°,
因为四边形ADD1A1,四边形CDD1C1均为矩形,
所以DD1⊥AD,DD1⊥CD,
设DD1=a,则AD1=CD1==,
在△ABC中,由余弦定理可得AC==6,
因为∠AD1C=90°,所以A+C=AC2,即2(a2+12)=36,解得a=(负值舍去).
故AA1=DD1=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教A版高中数学必修第二册
8.6 空间直线、平面的垂直
8.6.1 直线与直线垂直
基础过关练
题组一 求异面直线所成的角
1.(2024安徽六安期中)如图,已知正四棱锥P-ABCD的所有棱长均为2,E为棱PA的中点,则异面直线BE与PC所成角的余弦值为( )
A. B. C. D.
2.(2024山东威海模拟)在正方体ABCD-A1B1C1D1中,E,F分别为棱BC,B1C1的中点,若平面DBB1与平面AEF的交线为l,则l与直线AD1所成角的大小为( )
A. B. C. D.
3.(2023浙江绍兴期末)如图,已知正三棱柱ABC-A1B1C1中,AB=4,AA1=3,点M为A1B1的中点,则异面直线AM与B1C所成角的余弦值为 ( )
A. B. C. D.
4.(2024浙江杭州外国语学校期中)在正方体ABCD-A1B1C1D1中,M,N分别是BC1,CD1的中点.
(1)求异面直线CD1与BC1所成的角;
(2)求证:MN∥平面ABCD.
题组二 空间两条直线所成角的应用
5.(多选题)(2024山东德州夏津第一中学月考)已知E,F分别是三棱锥P-ABC的棱PA,BC的中点,且PC=6,AB=8.若异面直线PC与AB所成角的大小为60°,则线段EF的长可能为( )
A. B. C.5 D.
6.在长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,异面直线AB与A1C所成角的大小为,则该长方体的表面积与体积的比值是( )
A. B. C. D.4+
7.(2024广东深圳高级中学期中)如图,已知圆柱O1O2的底面半径和母线长均为1,B,A分别为上、下底面圆周上的点,若异面直线O1B,O2A所成的角为,则AB的长为 .
能力提升练
题组一 求异面直线所成的角
1.(2024浙江杭州第二中学期中)在正四面体S-ABC中,M是SC的中点,N是SB的中点,则异面直线BM与AN所成角的余弦值为( )
A. B. C. D.
2.(2024江苏南通期中)在圆锥PO中,轴截面PAB为等腰直角三角形,M为底面圆O上一点,∠AOM=30°,则异面直线OM与AP所成角的余弦值为( )
A. B. C. D.
3.当动点P在正方体ABCD-A1B1C1D1的棱DC上运动时,异面直线D1P与BC1所成角的取值范围是( )
A. B. C. D.
4.(2024贵州凯里第一中学模拟)平面α过直三棱柱ABC-A1B1C1的顶点B1,平面α∥平面ABC1,平面α∩平面BB1C1C=l,且AA1=AB=BC,AB⊥BC,则A1B与l所成角的正弦值为( )
A. B. C. D.
5.已知正三棱柱ABC-A1B1C1的侧面积为12,当其外接球的表面积取最小值时,异面直线AC1与B1C所成角的余弦值为 .
题组二 异面直线所成角的应用
6.(2024上海青浦高级中学期末)在棱长为1的正方体ABCD-
A1B1C1D1中,P为底面ABCD内(包括边界)的动点,满足直线D1P与CC1所成角的大小为,则线段DP扫过的面积为( )
A. B. C. D.
7.(2024广东阳江期末)在四面体A-BCD中,AB=CD=1,BC=2,且AB⊥BC,CD⊥BC,异面直线AB与CD所成的角为,则该四面体外接球的表面积为 .
8.(2022河南濮阳第一高级中学月考)在四棱柱ABCD-A1B1C1D1中,侧面都是矩形,底面ABCD是菱形且AB=BC=2,∠ABC=120°,若异面直线A1B和AD1所成的角为90°,求AA1的长度.
答案与分层梯度式解析
8.6 空间直线、平面的垂直
8.6.1 直线与直线垂直
基础过关练
1.B 2.C 3.A 5.BD 6.D
1.B 连接AC,取AC的中点O,连接OE,OB,则EO∥PC,EO=PC=1,故异面直线BE与PC所成的角为∠BEO(或其补角),
在△BEO中,EO=1,BO=,BE=,则由余弦定理的推论得cos∠BEO==,
故异面直线BE与PC所成角的余弦值为.
故选B.
解题模板 求异面直线所成角的一般步骤:
(1)作:通过作平行线或平移其中一条直线,构造异面直线所成角或其补角;
(2)证:证明所作的角或其补角为异面直线所成角;
(3)计算:一般在三角形中求角.
2.C 如图,因为E,F分别为棱BC,B1C1的中点,所以BB1∥EF,
因为EF 平面AEF,BB1 平面AEF,所以BB1∥平面AEF,
又平面DBB1∩平面AEF=l,BB1 平面DBB1,所以BB1∥l,
又AA1∥BB1,所以AA1∥l,所以l与直线AD1所成的角为∠A1AD1=.故选C.
3.A 如图所示,取AB的中点N,连接B1N,CN,
因为点M为A1B1的中点,A1B1=AB,所以MB1=AN,又MB1∥AN,所以四边形ANB1M为平行四边形,所以AM∥B1N,
所以异面直线AM与B1C所成的角为∠CB1N(或其补角),设∠CB1N=θ,
在正△ABC中,由AB=4,可得CN=2,
在直角△BNB1中,BB1=3,BN=2,所以B1N==,
在直角△BCB1中,BC=4,BB1=3,所以B1C==5,
在△B1CN中,由余弦定理的推论可得cos θ=
==.故选A.
4.解析 (1)连接A1B,A1C1,
因为A1D1=BC且A1D1∥BC,所以四边形A1D1CB为平行四边形,所以CD1∥A1B,
则∠A1BC1或其补角为异面直线CD1与BC1所成的角,
易知A1C1=A1B=BC1,所以△A1C1B为等边三角形,
所以∠A1BC1=60°,所以异面直线CD1与BC1所成的角为60°.
(2)证明:连接C1D,BD,则N为C1D的中点,
又M为BC1的中点,所以MN∥BD,
又MN 平面ABCD,BD 平面ABCD,
所以MN∥平面ABCD.
5.BD 如图,取AC的中点H,连接EH,FH,
因为E,F分别为PA,BC的中点,PC=6,AB=8,
所以AB∥HF,HE∥PC,HF=4,HE=3,
所以异面直线PC与AB所成的角即为∠EHF(或其补角),所以∠EHF=60°或∠EHF=120°.
当∠EHF=60°时,根据余弦定理的推论得cos∠EHF===,解得EF=;
当∠EHF=120°时,根据余弦定理的推论得cos∠EHF===-,解得EF=.故选BD.
易错警示 通过立体图形无法直接判断∠EHF是锐角还是钝角,因此∠EHF可能是异面直线所成的角,也可能是其补角,所以需要进行分类讨论.
6.D ∵AB∥DC,∴∠A1CD(或其补角)即为异面直线AB与A1C所成的角,由图可知∠A1CD为锐角,∴∠A1CD=.
设DD1=x,连接A1D,则A1C==,A1D=.
在△A1CD中,cos ==,解得x=(负值舍去),
∴长方体的表面积S=2+4×=2+4,体积V=,
∴该长方体的表面积与体积的比值为=4+.故选D.
7.答案 2或
解析 如图,过点A作AD垂直于上底面于点D,则AD是圆柱的母线,连接DB,DO1,
易知AD∥O1O2,AD=O1O2,
则四边形ADO1O2是平行四边形,∴O1D∥O2A,
∴O2A与O1B所成的角就是∠DO1B或其补角,
∴∠DO1B=或∠DO1B=.
当∠DO1B=时,△DO1B是等边三角形,BD=1,
在Rt△ABD中,AB==;
当∠DO1B=时,在△DO1B中,BD=2×=,
在Rt△ABD中,AB==2.
综上,AB=2或AB=.
能力提升练
1.A 2.A 3.C 4.A 6.A
1.A 取SM的中点E,连接EN,AE,如图,
∵N是SB的中点,∴EN∥MB,EN=MB,
∴∠ANE或其补角即为异面直线BM与AN所成的角.
设正四面体的棱长为4,
∵M是SC的中点,N是SB的中点,△SAB和△SBC均为正三角形,∴BM⊥SC,AN⊥SB,且BM=AN=2,∴EN=,
在△ASE中,由余弦定理得AE2=SA2+SE2-2SA·SE·cos∠ASE=16+1-2×4×1×=13,
在△ANE中,由余弦定理的推论得cos∠ANE===,
∴异面直线BM与AN所成角的余弦值为.故选A.
2.A 如图,过点A作AN∥OM,交圆O于点N,连接ON,PN,
则∠PAN或其补角即为异面直线OM与AP所成的角,
设AO=ON=1,易知∠OAN=∠ONA=∠AOM=30°,则AN=,
因为轴截面PAB为等腰直角三角形,所以PN=PA=,
在△APN中,由余弦定理的推论得cos∠PAN===,
所以异面直线OM与AP所成角的余弦值为.
故选A.
3.C 如图,连接AD1,AP,
易得AD1∥BC1,所以∠AD1P(或其补角)即为异面直线D1P与BC1所成的角.
设正方体的棱长为1,DP=x,x∈[0,1],
在△AD1P中,AD1=,AP=D1P=,
故cos∠AD1P==,
∵x∈[0,1],∴cos∠AD1P=∈,
又∠AD1P是△AD1P的内角,
∴∠AD1P∈,故选C.
4.A 如图所示,将直三棱柱ABC-A1B1C1补成直三棱柱ABC-A2B2C2,且AA1=A1A2,连接B1C2,A1C2,
则B1C2∥BC1,A1B1∥AB,
因为B1C2 平面ABC1,BC1 平面ABC1,所以B1C2∥平面ABC1,因为A1B1 平面ABC1,AB 平面ABC1,
所以A1B1∥平面ABC1,
又因为B1C2∩A1B1=B1,且B1C2,A1B1 平面A1B1C2,
所以平面A1B1C2∥平面ABC1,又B1∈平面A1B1C2,所以平面A1B1C2即为平面α,所以l即为直线B1C2,
因为B1C2∥BC1,所以A1B与l所成的角为∠A1BC1(或其补角),
由AA1=AB=BC,AB⊥BC,可得A1C1=BC1=BA1,
所以△A1BC1为等边三角形,所以∠A1BC1=60°,所以sin∠A1BC1=,即A1B与l所成角的正弦值为.
故选A.
小题速解 因为平面α∥平面ABC1,平面α∩平面BB1C1C=l,平面ABC1∩平面BB1C1C=BC1,
所以l∥BC1,则A1B与l所成的角为∠A1BC1(或其补角),
下同解析.
5.答案
解析 设正三棱柱的底面边长为a,高为h,外接球的半径为R,由题意知3ah=12,即ah=4,
易得△ABC外接圆的半径r==,
则R2=r2+=+≥=,当且仅当a=h时取等号,此时外接球的表面积最小.
将三棱柱补成一个四棱柱,如图,连接DB1,DC,
则AC1∥DB1,∴∠DB1C(或其补角)为异面直线AC1与B1C所成的角,易得B1C=DB1=,DC=a,
∴cos∠DB1C==.
解题技法 补形平移是常用的一种作平行线的方法,一般是补一个相同形状的几何体,构成一个特殊的几何体,方便作平行线,如此题将三棱柱补成一个四棱柱.
6.A 因为DD1∥CC1,所以直线D1P与CC1所成的角即为DD1与D1P所成的角,
易知DD1⊥PD,所以DD1与D1P所成的角为∠DD1P,即∠DD1P=,故tan∠DD1P==,即DP=,
所以点P的轨迹是以D为圆心,为半径的圆的四分之一,
故线段DP扫过的面积为π×=.
故选A.
7.答案 或8π
解析 由题意,可以将四面体A-BCD补成一个直三棱柱,如图所示.
∵CD∥BE,∴直线AB与CD所成的角为∠ABE或其补角,
∵异面直线AB与CD所成的角为,
∴∠ABE=或∠ABE=.
设△ABE外接圆的半径为r,当∠ABE=时,AE=BE=AB=1,则2r=,解得r=;
当∠ABE=时,AE=,
则2r=,解得r=1.
设四面体外接球的半径为R,
则R==,∴R=或R=,
则外接球的表面积为或8π.
8.解析 如图,连接AC,CD1,
在四棱柱ABCD-A1B1C1D1中,A1D1∥BC且A1D1=BC,
所以四边形A1BCD1为平行四边形,所以A1B∥CD1,
所以异面直线A1B和AD1所成的角为∠AD1C,故∠AD1C=90°,
因为四边形ADD1A1,四边形CDD1C1均为矩形,
所以DD1⊥AD,DD1⊥CD,
设DD1=a,则AD1=CD1==,
在△ABC中,由余弦定理可得AC==6,
因为∠AD1C=90°,所以A+C=AC2,即2(a2+12)=36,解得a=(负值舍去).
故AA1=DD1=.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
