2025人教A版高中数学必修第二册强化练习题--9.2.3 总体集中趋势的估计 9.2.4 总体离散程度的估计
文档属性
| 名称 | 2025人教A版高中数学必修第二册强化练习题--9.2.3 总体集中趋势的估计 9.2.4 总体离散程度的估计 |

|
|
| 格式 | docx | ||
| 文件大小 | 504.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025人教A版高中数学必修第二册
9.2.3 总体集中趋势的估计 9.2.4 总体离散程度的估计
基础过关练
题组一 平均数、中位数、众数
1.(2024江苏苏州张家港开学考试)某歌唱比赛共有11位评委给某选手进行评分,评定该选手的成绩时,从11个原始评分中去掉1个最高分、1个最低分,得到9个有效评分.9个有效评分与11个原始评分相比,一定不变的数字特征是( )
A.平均数 B.极差 C.方差 D.中位数
2.(2024上海实验学校开学考试)某学校艺术节举行弹钢琴比赛,现有21名同学报名参赛,初赛成绩各不相同,取前10名参加决赛,小明同学已经知道了自己的成绩,为了判断自己是否能进入决赛,他还需要知道21名同学成绩的( )
A.平均数 B.中位数 C.众数 D.方差
3.(2024江苏南通模拟)某同学测得自己所在城市连续7天的最低气温分别为1,2,2,m,6,2,8(单位:℃),若这组数据的平均数是中位数的2倍,则m=( )
A.2 B.3 C.6 D.7
4.(2023山东济南模拟)某射击运动员连续射击5次,命中的环数(环数为整数)形成的一组数据中,中位数为8,唯一的众数为9,极差为3,则该组数据的平均数为( )
A.7.6 B.7.8 C.8 D.8.2
5.(多选题)(2024山西太原师范学院附属中学开学考试)某单位为了解该单位党员开展学习党史知识活动的情况,随机抽取了30名党员,对他们一周的党史学习时间进行了统计,统计数据如下表.
党史学习时间/h 7 8 9 10 11
党员人数 4 8 7 6 5
则下列对该单位党员一周的党史学习时间的叙述正确的有( )
A.众数是8 h B.第40百分位数为8 h
C.平均数是9 h D.上四分位数是10 h
6.据了解,某公司的33名职工月工资(单位:元)如下表:
职务 董事长 副董 事长 董事 总经理 经理 管理员 职员
人数 1 1 2 1 5 3 20
工资 11 000 10 000 9 000 8 000 6 500 5 500 4 000
(1)求该公司职工月工资的平均数、中位数、众数;
(2)假设副董事长的工资从10 000元提升到20 000元,董事长的工资从11 000元提升到30 000元,那么新的平均数、中位数、众数又是什么 (精确到元)
(3)你认为哪个统计量更能反映这个公司员工的工资水平 结合此问题谈一谈你的看法.
题组二 频率分布直方图与平均数、中位数、众数
7.(2024湖北武汉模拟)如图的频率分布直方图显示了三种不同的形态.图1形成对称形态,图2形成“右拖尾”形态,图3形成“左拖尾”形态,则下列判断不正确的是( )
A.图1的平均数=中位数=众数
B.图2的众数<中位数<平均数
C.图2的平均数<众数<中位数
D.图3的平均数<中位数<众数
8.(2024陕西西安期中)学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出(单位:元)在[20,60]内的样本,其频率分布直方图如图所示(同一组中数据用该组区间的中点值作代表),则下列说法正确的是 ( )
A.估计众数为43元
B.估计中位数是元
C.估计平均数为43元
D.支出在[50,60)内的频率为0.25
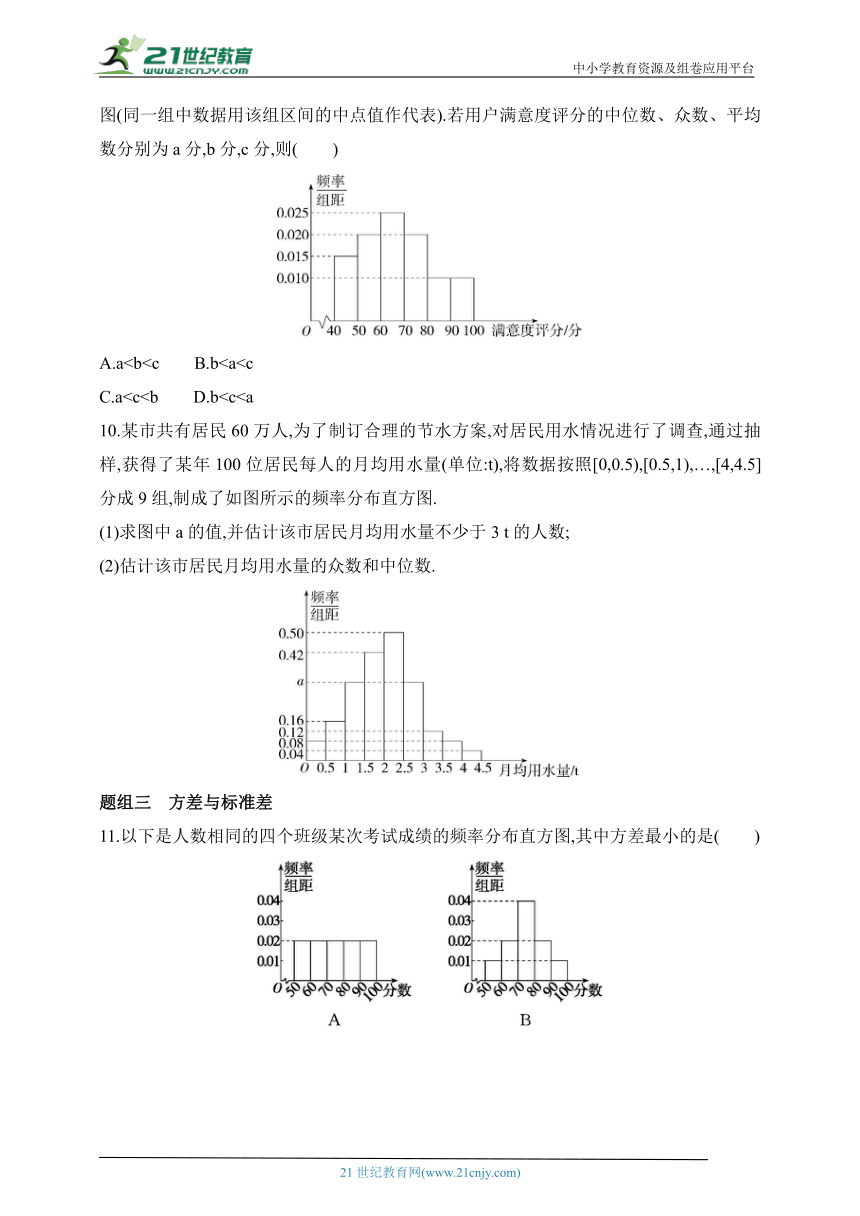
9.(2023四川成都联考)某公司为了解用户对该公司生产的产品的满意度,从使用该产品的用户中随机调查了100位,根据用户对产品的满意度评分,得到如图所示的频率分布直方图(同一组中数据用该组区间的中点值作代表).若用户满意度评分的中位数、众数、平均数分别为a分,b分,c分,则( )
A.aC.a10.某市共有居民60万人,为了制订合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:t),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(1)求图中a的值,并估计该市居民月均用水量不少于3 t的人数;
(2)估计该市居民月均用水量的众数和中位数.
题组三 方差与标准差
11.以下是人数相同的四个班级某次考试成绩的频率分布直方图,其中方差最小的是( )
12.(2024湖北武汉外国语学校月考)已知样本数据x1,x2,…,x2 022的平均数和方差分别为3和56,若yi=2xi+3(i=1,2,…,2 022),则y1,y2,…,
y2 022的平均数和方差分别是( )
A.12,115 B.12,224
C.9,115 D.9,224
13.(2024四川双流棠湖中学月考)第31届世界大学生夏季运动会于2021年8月18日至8月29日在成都举行,举办方招募志愿者在赛事期间为运动会提供咨询、交通引导、场馆周边秩序维护等服务,招募的志愿者需接受专业培训,甲、乙两名志愿者在培训过程中进行了六次测试,其测试成绩(单位:分)如折线图所示:
则下列说法正确的是( )
A.甲的平均成绩比乙的平均成绩高
B.甲的平均成绩比乙的平均成绩低
C.甲成绩的极差比乙成绩的极差小
D.乙的成绩比甲的成绩稳定
14.(2024河北保定曲阳第一高级中学月考)已知甲队有60人,乙队有40人,按照分层随机抽样的方法从两队共抽取10人进行一轮答题.相关统计情况如下:甲队答对题目的平均数为1,方差为1;乙队答对题目的平均数为1.5,方差为0.4.则这10人答对题目的方差为( )
A.0.8 B.0.675 C.0.74 D.0.82
15.(2024湖南长沙第一中学期中)设一组样本数据x1,x2,…,x10的平均值是1,且,,…,的平均值是3,则数据x1,x2,…,x10的方差是 .
16.甲、乙两机床同时加工直径为100 cm的零件,为检验质量,从中各抽取6件零件进行测量,数据如下.
甲 99 100 98 100 100 103
乙 99 100 102 99 100 100
(1)分别计算两组数据的平均数及方差;
(2)根据计算结果判断哪台机床加工的零件的质量更稳定.
能力提升练
题组 样本数字特征的估计
1.(多选题)(2024广东茂名高州模拟)某校举行与中秋节相关的“中国传统文化”知识竞赛,随机抽查了100人的成绩,整理后得到如图所示的频率分布直方图,则下列结论正确的是( )
A.样本的众数为75
B.样本的71%分位数为75
C.样本的平均值为68.5
D.该校学生中得分低于60分的约占20%
2.(多选题)(2024海南海口模拟)已知甲、乙两个样本各有10个数据,甲、乙两组数据合并后得到一组新数据,下列说法正确的是 ( )
A.若甲、乙两组数据的平均数都为a,则新数据的平均数等于a
B.若甲、乙两组数据的极差都为b,则新数据的极差可能大于b
C.若甲、乙两组数据的方差都为c,则新数据的方差可能小于c
D.若甲、乙两组数据的中位数都为d,则新数据的中位数等于d
3.(多选题)(2024湖北荆州月考)某班语文老师对该班甲、乙、丙、丁4名同学连续7周每周阅读的天数(每周阅读天数可以是1,2,3,4,5,6,7)进行统计,根据统计数据进行了如下描述:
甲:中位数为4,极差为3;
乙:中位数为3,众数为5;
丙:中位数为4,平均数为3;
丁:平均数为3,方差为3.
那么可以判断一周阅读天数一定没有出现7天的是( )
A.甲 B.乙 C.丙 D.丁
4.为了解学生的课外阅读情况,某校采用样本量比例分配的分层随机抽样对高中三个年级的学生进行平均每周课外阅读时间(单位:h)的调查,所得样本数据如下:
年级 抽样人数 样本平均数 样本方差
高一 40 5 3.5
高二 30 2
高三 30 3
已知高中三个年级学生的总样本平均数为4.1,总样本方差为3.14,则高二年级学生的样本平均数= ,高三年级学生的样本方差= .
5.(2024广西崇左钦州名校联考)某单位举办演讲比赛,最终来自A,B,C,D四个部门共12人进入决赛,把这四个部门进入决赛的人数作为样本数据.已知样本方差为2.5,且样本数据互不相同,则样本数据中的最大值为 .
6.(2024浙江余姚中学期中)某学校举办了一场党史知识竞赛活动,共有500名学生参加.为了解本次知识竞赛活动的成绩,从中抽取了50名学生的分数(分数均为整数,满分为100分)进行统计,所有学生的分数都不低于60,将这50名学生的分数进行分组,第一组[60,70),第二组[70,80),第三组[80,90),第四组[90,100],得到如下频率分布直方图.
(1)求图中m的值,并估计此次知识竞赛活动学生分数的中位数;
(2)根据频率分布直方图,估计此次知识竞赛活动学生分数的平均数(同一组中的数据用该组区间的中点值作代表).若对分数不低于平均数的同学进行奖励,请估计参赛的500名学生中获奖的人数.
7.为满足广大市民的日常生活所需,某快递公司以优厚的条件招聘派送员,现给出了两种日薪方案:
甲方案:底薪100元,每派送一单奖励1元;
乙方案:底薪150元,每日前55单没有奖励,超过55单的部分每单奖励10元.
(1)请分别求出这两种薪酬方案中日薪y(单位:元)与送货单数n的函数关系式;
(2)根据该公司所有派送员10天的派送记录,得到派送员的日均派送单数与天数的数据如下表:
日均派送单数 50 54 56 58 60
频数/天 2 3 2 2 1
回答下列问题:
①根据以上数据,设每名派送员的日薪为X(单位:元),试分别求出这10天中甲、乙两种方案的日薪X的平均数及方差;
②结合①中的数据,根据统计学的思想,若你去应聘派送员,选择哪种薪酬方案比较合适 并说明你的理由.
答案与分层梯度式解析
9.2.3 总体集中趋势的估计
9.2.4 总体离散程度的估计
基础过关练
1.D 2.B 3.D 4.B 5.ACD 7.C 8.B 9.B
11.B 12.D 13.D 14.D
1.D 设11位评委的评分按从小到大排列为x1,x2,x3,x4,…,x8,x9,x10,x11.
则原始数据的中位数为x6,去掉最低分x1,最高分x11,剩余x2,x3,x4,…,x8,x9,x10,中位数仍为x6,其余数字特征可能改变.故选D.
2.B 易得21名同学成绩的中位数是第11名同学的成绩,取前10名参加决赛,小明同学已经知道了自己的成绩,为了判断自己是否能进入决赛,他还需要知道第11名同学的成绩.故选B.
3.D 这组数据的平均数为=,
除m外,将数据按从小到大排列为1,2,2,2,6,8,
结合m的任意性可知中位数为2,则=2×2,解得m=7.故选D.
4.B 依题意知这组数据一共有5个数,中位数为8,则将数据从小到大排列,8是第3个数,
又唯一的众数为9,所以有两个9,其余数字均只出现一次,且这5个数中的最大数为9,因为极差为3,所以最小的数为6,
故这组数据为6,7,8,9,9,则平均数为=7.8.故选B.
5.ACD 由题表可知,党史学习时间为8 h的人最多,为8人,故众数是8 h,A正确;
∵30×40%=12,∴第40百分位数为=8.5(h),故B错误;
平均数为×(7×4+8×8+9×7+10×6+11×5)=9(h),故C正确;
∵30×75%=22.5,∴上四分位数为10 h,故D正确.故选ACD.
6.解析 (1)平均数=4 000+×(7 000+6 000+5 000×2+4 000+
2 500×5+1 500×3+0×20)≈5 333(元),
中位数是4 000元,众数是4 000元.
(2)平均数=4 000+×(26 000+16 000+5 000×2+4 000+2 500×5+
1 500×3+0×20)≈6 212(元),中位数是4 000元,众数是4 000元.
(3)中位数和众数均能反映该公司员工的工资水平,因为公司中职员与董事长的工资相差较多,
这样导致平均数与中位数(众数)偏差较大(平均数受极端值影响较大),
所以平均数不能反映这个公司员工的工资水平.
解后反思
众数、中位数和平均数的比较
名称 优点 缺点
平均数 与中位数相比,平均数反映出样本数据中更多的信息,对样本中的极端值更加敏感 样本中的任何一个数据的改变都会引起平均数的改变.数据越“离群”,对平均数的影响越大
中位数 不受少数几个极端数据(即排序靠前或靠后的数据)的影响 对极端值不敏感
众数 体现了样本数据的最大集中点 只能传递数据中一部分信息,对极端值不敏感
7.C 题图1是对称的,所以平均数=中位数=众数,故A中判断正确;
题图2中众数最小,“右拖尾”表现为平均数大于中位数,故B中判断正确,C中判断错误;
题图3“左拖尾”表现为众数最大,平均数小于中位数,故D中判断正确.
故选C.
8.B 由题图知,支出在[40,50)内的小矩形最高,故估计众数为45元,A错;
支出在[50,60)内的频率为1-(0.01+0.024+0.036)×10=0.3,D错;
因为10×(0.01+0.024)=0.34<0.5,0.34+10×0.036=0.7,所以中位数在[40,50)内,设中位数为x元,则0.34+(x-40)×0.036=0.5,解得x=,故中位数是元,B正确;
平均数为10×(0.01×25+0.024×35+0.036×45)+0.3×55=43.6元,C错.
故选B.
9.B 由题中频率分布直方图可知众数为65,即b=65,
平均数为45×0.15+55×0.2+65×0.25+75×0.2+85×0.1+95×0.1=67,即c=67,
因为10×(0.015+0.020)=0.35<0.5,0.35+0.025×10=0.6>0.5,所以中位数位于区间[60,70),
则有0.35+(a-60)×0.025=0.5,解得a=66,
所以b10.解析 (1)由题图可得(0.04+0.08×2+0.12+0.16+2a+0.42+0.50)×0.5=1,解得a=0.3.
估计该市居民月均用水量不少于3 t的人数为(0.12+0.08+0.04)×0.5×60×104=72 000.
(2)由题图可估计该市居民月均用水量的众数为(2+2.5)÷2=2.25(t).设中位数为x t,
因为(0.08+0.16+0.3+0.42)×0.5=0.48<0.5,0.48+0.50×0.5=0.73>0.5,所以2由0.48+(x-2)×0.5=0.5,解得x=2.04,
故估计该市居民月均用水量的中位数为2.04 t.
11.B 方差表示数据波动性的大小、稳定程度.数据越均数,方差越小,结合题图可知,B中数据主要集中在70~80内,且波动性小,故方差最小.
12.D 设数据x1,x2,…,xn的平均数和方差分别为和s2,则数据ax1+b,ax2+b,…,axn+b的平均数和方差分别为a+b和a2s2,所以y1,y2,…,y2 022的平均数为2×3+3=9,方差为22×56=224.故选D.
13.D 由题中折线图得到甲六次测试的成绩(单位:分)依次为90,93,92,94,96,93,
乙六次测试的成绩(单位:分)依次为93,94,91,95,92,93,
则甲的平均成绩为×(90+93+92+94+96+93)=93,
乙的平均成绩为×(93+94+91+95+92+93)=93,故A,B均错误;
甲成绩的极差为96-90=6,乙成绩的极差为95-91=4,故C错误;
甲成绩的方差=×[(-3)2+02+(-1)2+12+32+02]=,
乙成绩的方差=×[02+12+(-2)2+22+(-1)2+02]=,
因为>,所以乙的成绩比甲的成绩稳定,D正确.故选D.
14.D 按照分层随机抽样的方法从甲队中抽取10×=6人,从乙队中抽取10×=4人,
这10人答对题目的平均数为×(6×1+4×1.5)=1.2,
所以这10人答对题目的方差为×{6×[1+(1-1.2)2]+4×[0.4+(1.5-1.2)2]}=0.82.故选D.
解题模板 若一个总体划分为两层,各层抽取的样本量、样本平均数和样本方差分别为m,,;n,,.记总的样本平均数为,样本方差为s2,则=+;s2={m[+]+n[+]}.
15.答案 2
解析 由题意得数据x1,x2,…,x10的方差s2=-=3-12=2.
故答案为2.
解后反思 方差的计算公式有两种形式,即s2=(xi-)2和s2=-,可以根据题目条件灵活选择.
16.解析 (1)==100,==100,
==,==1.
(2)∵两台机床所加工的零件的直径的平均值相同,>,
∴乙机床加工的零件的质量更稳定.
能力提升练
1.AC 2.ABD 3.BCD
1.AC 依题意得(0.015+0.025+0.035+0.005+2a)×10=1,解得a=0.010.
∵最高小矩形底边中点的横坐标为75,
∴众数是75,故A正确;
设样本的71%分位数为x,∵10×(0.010+0.015+0.025)=0.5,0.5+10×0.035=0.85,∴0.5+(x-70)×0.035=0.71,解得x=76,故B错误;
平均值为45×0.1+55×0.15+65×0.25+75×0.35+85×0.1+95×0.05=68.5,故C正确;
样本中得分低于60分的占(0.010+0.015)×10×100%=25%,∴该校学生中得分低于60分的约占25%,故D错误.
故选AC.
2.ABD 设甲:x1,x2,…,x10,乙:y1,y2,…,y10,新数据为z1,z2,…,z20.
对于A,=(z1+z2+…+z20)=(10a+10a)=a,A正确;
对于B,设甲:1,2,…,10,乙:21,22,…,30,则甲、乙两组数据的极差均为9,但混合后数据的极差为29,B正确;
对于C,因为(++…+-10)=(++…+-10)=c,所以++…+=10c+10,++…+=10c+10,=,
所以新数据的方差为(++…++++…+-20)=(10c+10+10c+10-20)=c+,
因为+-2=+-2×=≥0,
所以新数据的方差一定不小于c,C错误;
对于D,不妨设x1≤x2≤…≤x10,y1≤y2≤…≤y10,则d==,
将混合后的数据按从小到大排列,
若x5≤y5,则x6≥y6,所以第10,11个数为y5和y6,
若x5>y5,则x6两种情形下,新数据的中位数都等于d,D正确.
故选ABD.
3.BCD 对于甲,中位数为4,极差为3,所以这7个数可以是4,4,4,4,4,4,7,则甲不符合题意;
对于乙,中位数为3,众数为5,所以这7个数从小到大排列后,第4个数是3,
所以1,2,3中一定有一个数出现2次,5出现3次,所以这7个数中一定没有出现7,则乙符合题意;
对于丙,若出现1个7,则这7个数从小到大排列后,后4个数之和最小为19,前3个数之和最小为3,从而这7个数的平均数最小为>3,即这7个数的平均数不可能为3,所以数据中不可能出现7,故丙符合题意;
对于丁,设这7个数分别为x1,x2,x3,x4,x5,x6,x7,则x1+x2+x3+x4+x5+x6+x7=21,
(x1-3)2+(x2-3)2+(x3-3)2+(x4-3)2+(x5-3)2+(x6-3)2+(x7-3)2=21,
若x1=7,则x2+x3+x4+x5+x6+x7=14,
(x2-3)2+(x3-3)2+(x4-3)2+(x5-3)2+(x6-3)2+(x7-3)2=5,
从而x2,x3,x4,x5,x6,x7这6个数可能是4,4,4,4,4,3或4,4,4,4,3,2或4,4,4,3,2,2或4,4,3,2,2,2或4,3,2,2,2,2或3,2,2,2,2,2或5,4,3,3,3,3或5,3,3,3,3,2或4,3,3,3,3,1或3,3,3,3,2,1,这与x2+x3+x4+x5+x6+x7=14矛盾,
即这7个数中一定没有出现7,故丁符合题意.
故选BCD.
4.答案 4;1.5
解析 由高中三个年级学生的总样本平均数为4.1,
可得=4.1,解得=4.
因为总样本方差为3.14,所以×[3.5+(5-4.1)2]+×[2+(4-4.1)2]+×[+(3-4.1)2]=3.14,
解得=1.5.
故答案为4;1.5.
5.答案 5
解析 设样本数据为a,b,c,d,且a则样本平均数为=3,样本方差为×[(a-3)2+(b-3)2+(c-3)2+(d-3)2]=,
则(a-3)2+(b-3)2+(c-3)2+(d-3)2=10,
所以(d-3)2≤10,解得d≤+3.
当d=6时,(a-3)2+(b-3)2+(c-3)2=1,因为样本数据互不相同,所以不存在a,b,c使得等式成立.
当d=5时,(a-3)2+(b-3)2+(c-3)2=6,存在a=1,b=2,c=4,使得等式成立,故样本数据中的最大值为5.
6.解析 (1)由题中频率分布直方图知(0.01+m+0.04+0.02)×10=1,解得m=0.03.
设此次知识竞赛活动学生分数的中位数为x0,
因为数据落在[60,80)内的频率为0.4,落在[60,90)内的频率为0.8,所以80由(x0-80)×0.04=0.5-0.4,得x0=82.5,
故估计此次知识竞赛活动学生分数的中位数为82.5.
(2)由题中频率分布直方图及(1)知数据落在[60,70),[70,80),[80,90),[90,100]内的频率分别为0.1,0.3,0.4,0.2,则估计此次知识竞赛活动学生分数的平均数为65×0.1+75×0.3+85×0.4+95×0.2=82.
此次知识竞赛活动学生分数不低于82的频率为0.2+×0.4=0.52,
故估计参赛的500名学生中获奖的人数为500×0.52=260.
7.解析 (1)由题意可知,甲方案日薪y与送货单数n的函数关系式为y=n×1+100=n+100,n∈N.
对于乙方案,当n≤55,n∈N时,y=150;
当n>55,n∈N时,y=150+(n-55)×10=10n-400.
故乙方案日薪y与送货单数n的函数关系式为
y=
(2)①甲方案日薪X的平均数==155(元),
方差=×[2×(150-155)2+3×(154-155)2+2×(156-155)2+2×(158-155)2+(160-155)2]
=×(50+3+2+18+25)=9.8.
乙方案日薪X的平均数==163(元),
方差=×[2×(150-163)2+3×(150-163)2+2×(160-163)2+2×(180-163)2+(200-163)2]
=×(338+507+18+578+1 369)=281.
②答案一:由①可知<,则选择乙方案比较合适.
答案二:由①可知,<,二者相差不大,>,二者相差较大,即甲方案日薪波动情况比乙小得多,则选择甲方案比较合适.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教A版高中数学必修第二册
9.2.3 总体集中趋势的估计 9.2.4 总体离散程度的估计
基础过关练
题组一 平均数、中位数、众数
1.(2024江苏苏州张家港开学考试)某歌唱比赛共有11位评委给某选手进行评分,评定该选手的成绩时,从11个原始评分中去掉1个最高分、1个最低分,得到9个有效评分.9个有效评分与11个原始评分相比,一定不变的数字特征是( )
A.平均数 B.极差 C.方差 D.中位数
2.(2024上海实验学校开学考试)某学校艺术节举行弹钢琴比赛,现有21名同学报名参赛,初赛成绩各不相同,取前10名参加决赛,小明同学已经知道了自己的成绩,为了判断自己是否能进入决赛,他还需要知道21名同学成绩的( )
A.平均数 B.中位数 C.众数 D.方差
3.(2024江苏南通模拟)某同学测得自己所在城市连续7天的最低气温分别为1,2,2,m,6,2,8(单位:℃),若这组数据的平均数是中位数的2倍,则m=( )
A.2 B.3 C.6 D.7
4.(2023山东济南模拟)某射击运动员连续射击5次,命中的环数(环数为整数)形成的一组数据中,中位数为8,唯一的众数为9,极差为3,则该组数据的平均数为( )
A.7.6 B.7.8 C.8 D.8.2
5.(多选题)(2024山西太原师范学院附属中学开学考试)某单位为了解该单位党员开展学习党史知识活动的情况,随机抽取了30名党员,对他们一周的党史学习时间进行了统计,统计数据如下表.
党史学习时间/h 7 8 9 10 11
党员人数 4 8 7 6 5
则下列对该单位党员一周的党史学习时间的叙述正确的有( )
A.众数是8 h B.第40百分位数为8 h
C.平均数是9 h D.上四分位数是10 h
6.据了解,某公司的33名职工月工资(单位:元)如下表:
职务 董事长 副董 事长 董事 总经理 经理 管理员 职员
人数 1 1 2 1 5 3 20
工资 11 000 10 000 9 000 8 000 6 500 5 500 4 000
(1)求该公司职工月工资的平均数、中位数、众数;
(2)假设副董事长的工资从10 000元提升到20 000元,董事长的工资从11 000元提升到30 000元,那么新的平均数、中位数、众数又是什么 (精确到元)
(3)你认为哪个统计量更能反映这个公司员工的工资水平 结合此问题谈一谈你的看法.
题组二 频率分布直方图与平均数、中位数、众数
7.(2024湖北武汉模拟)如图的频率分布直方图显示了三种不同的形态.图1形成对称形态,图2形成“右拖尾”形态,图3形成“左拖尾”形态,则下列判断不正确的是( )
A.图1的平均数=中位数=众数
B.图2的众数<中位数<平均数
C.图2的平均数<众数<中位数
D.图3的平均数<中位数<众数
8.(2024陕西西安期中)学校为了调查学生在课外读物方面的支出情况,抽出了一个容量为n且支出(单位:元)在[20,60]内的样本,其频率分布直方图如图所示(同一组中数据用该组区间的中点值作代表),则下列说法正确的是 ( )
A.估计众数为43元
B.估计中位数是元
C.估计平均数为43元
D.支出在[50,60)内的频率为0.25
9.(2023四川成都联考)某公司为了解用户对该公司生产的产品的满意度,从使用该产品的用户中随机调查了100位,根据用户对产品的满意度评分,得到如图所示的频率分布直方图(同一组中数据用该组区间的中点值作代表).若用户满意度评分的中位数、众数、平均数分别为a分,b分,c分,则( )
A.a
(1)求图中a的值,并估计该市居民月均用水量不少于3 t的人数;
(2)估计该市居民月均用水量的众数和中位数.
题组三 方差与标准差
11.以下是人数相同的四个班级某次考试成绩的频率分布直方图,其中方差最小的是( )
12.(2024湖北武汉外国语学校月考)已知样本数据x1,x2,…,x2 022的平均数和方差分别为3和56,若yi=2xi+3(i=1,2,…,2 022),则y1,y2,…,
y2 022的平均数和方差分别是( )
A.12,115 B.12,224
C.9,115 D.9,224
13.(2024四川双流棠湖中学月考)第31届世界大学生夏季运动会于2021年8月18日至8月29日在成都举行,举办方招募志愿者在赛事期间为运动会提供咨询、交通引导、场馆周边秩序维护等服务,招募的志愿者需接受专业培训,甲、乙两名志愿者在培训过程中进行了六次测试,其测试成绩(单位:分)如折线图所示:
则下列说法正确的是( )
A.甲的平均成绩比乙的平均成绩高
B.甲的平均成绩比乙的平均成绩低
C.甲成绩的极差比乙成绩的极差小
D.乙的成绩比甲的成绩稳定
14.(2024河北保定曲阳第一高级中学月考)已知甲队有60人,乙队有40人,按照分层随机抽样的方法从两队共抽取10人进行一轮答题.相关统计情况如下:甲队答对题目的平均数为1,方差为1;乙队答对题目的平均数为1.5,方差为0.4.则这10人答对题目的方差为( )
A.0.8 B.0.675 C.0.74 D.0.82
15.(2024湖南长沙第一中学期中)设一组样本数据x1,x2,…,x10的平均值是1,且,,…,的平均值是3,则数据x1,x2,…,x10的方差是 .
16.甲、乙两机床同时加工直径为100 cm的零件,为检验质量,从中各抽取6件零件进行测量,数据如下.
甲 99 100 98 100 100 103
乙 99 100 102 99 100 100
(1)分别计算两组数据的平均数及方差;
(2)根据计算结果判断哪台机床加工的零件的质量更稳定.
能力提升练
题组 样本数字特征的估计
1.(多选题)(2024广东茂名高州模拟)某校举行与中秋节相关的“中国传统文化”知识竞赛,随机抽查了100人的成绩,整理后得到如图所示的频率分布直方图,则下列结论正确的是( )
A.样本的众数为75
B.样本的71%分位数为75
C.样本的平均值为68.5
D.该校学生中得分低于60分的约占20%
2.(多选题)(2024海南海口模拟)已知甲、乙两个样本各有10个数据,甲、乙两组数据合并后得到一组新数据,下列说法正确的是 ( )
A.若甲、乙两组数据的平均数都为a,则新数据的平均数等于a
B.若甲、乙两组数据的极差都为b,则新数据的极差可能大于b
C.若甲、乙两组数据的方差都为c,则新数据的方差可能小于c
D.若甲、乙两组数据的中位数都为d,则新数据的中位数等于d
3.(多选题)(2024湖北荆州月考)某班语文老师对该班甲、乙、丙、丁4名同学连续7周每周阅读的天数(每周阅读天数可以是1,2,3,4,5,6,7)进行统计,根据统计数据进行了如下描述:
甲:中位数为4,极差为3;
乙:中位数为3,众数为5;
丙:中位数为4,平均数为3;
丁:平均数为3,方差为3.
那么可以判断一周阅读天数一定没有出现7天的是( )
A.甲 B.乙 C.丙 D.丁
4.为了解学生的课外阅读情况,某校采用样本量比例分配的分层随机抽样对高中三个年级的学生进行平均每周课外阅读时间(单位:h)的调查,所得样本数据如下:
年级 抽样人数 样本平均数 样本方差
高一 40 5 3.5
高二 30 2
高三 30 3
已知高中三个年级学生的总样本平均数为4.1,总样本方差为3.14,则高二年级学生的样本平均数= ,高三年级学生的样本方差= .
5.(2024广西崇左钦州名校联考)某单位举办演讲比赛,最终来自A,B,C,D四个部门共12人进入决赛,把这四个部门进入决赛的人数作为样本数据.已知样本方差为2.5,且样本数据互不相同,则样本数据中的最大值为 .
6.(2024浙江余姚中学期中)某学校举办了一场党史知识竞赛活动,共有500名学生参加.为了解本次知识竞赛活动的成绩,从中抽取了50名学生的分数(分数均为整数,满分为100分)进行统计,所有学生的分数都不低于60,将这50名学生的分数进行分组,第一组[60,70),第二组[70,80),第三组[80,90),第四组[90,100],得到如下频率分布直方图.
(1)求图中m的值,并估计此次知识竞赛活动学生分数的中位数;
(2)根据频率分布直方图,估计此次知识竞赛活动学生分数的平均数(同一组中的数据用该组区间的中点值作代表).若对分数不低于平均数的同学进行奖励,请估计参赛的500名学生中获奖的人数.
7.为满足广大市民的日常生活所需,某快递公司以优厚的条件招聘派送员,现给出了两种日薪方案:
甲方案:底薪100元,每派送一单奖励1元;
乙方案:底薪150元,每日前55单没有奖励,超过55单的部分每单奖励10元.
(1)请分别求出这两种薪酬方案中日薪y(单位:元)与送货单数n的函数关系式;
(2)根据该公司所有派送员10天的派送记录,得到派送员的日均派送单数与天数的数据如下表:
日均派送单数 50 54 56 58 60
频数/天 2 3 2 2 1
回答下列问题:
①根据以上数据,设每名派送员的日薪为X(单位:元),试分别求出这10天中甲、乙两种方案的日薪X的平均数及方差;
②结合①中的数据,根据统计学的思想,若你去应聘派送员,选择哪种薪酬方案比较合适 并说明你的理由.
答案与分层梯度式解析
9.2.3 总体集中趋势的估计
9.2.4 总体离散程度的估计
基础过关练
1.D 2.B 3.D 4.B 5.ACD 7.C 8.B 9.B
11.B 12.D 13.D 14.D
1.D 设11位评委的评分按从小到大排列为x1,x2,x3,x4,…,x8,x9,x10,x11.
则原始数据的中位数为x6,去掉最低分x1,最高分x11,剩余x2,x3,x4,…,x8,x9,x10,中位数仍为x6,其余数字特征可能改变.故选D.
2.B 易得21名同学成绩的中位数是第11名同学的成绩,取前10名参加决赛,小明同学已经知道了自己的成绩,为了判断自己是否能进入决赛,他还需要知道第11名同学的成绩.故选B.
3.D 这组数据的平均数为=,
除m外,将数据按从小到大排列为1,2,2,2,6,8,
结合m的任意性可知中位数为2,则=2×2,解得m=7.故选D.
4.B 依题意知这组数据一共有5个数,中位数为8,则将数据从小到大排列,8是第3个数,
又唯一的众数为9,所以有两个9,其余数字均只出现一次,且这5个数中的最大数为9,因为极差为3,所以最小的数为6,
故这组数据为6,7,8,9,9,则平均数为=7.8.故选B.
5.ACD 由题表可知,党史学习时间为8 h的人最多,为8人,故众数是8 h,A正确;
∵30×40%=12,∴第40百分位数为=8.5(h),故B错误;
平均数为×(7×4+8×8+9×7+10×6+11×5)=9(h),故C正确;
∵30×75%=22.5,∴上四分位数为10 h,故D正确.故选ACD.
6.解析 (1)平均数=4 000+×(7 000+6 000+5 000×2+4 000+
2 500×5+1 500×3+0×20)≈5 333(元),
中位数是4 000元,众数是4 000元.
(2)平均数=4 000+×(26 000+16 000+5 000×2+4 000+2 500×5+
1 500×3+0×20)≈6 212(元),中位数是4 000元,众数是4 000元.
(3)中位数和众数均能反映该公司员工的工资水平,因为公司中职员与董事长的工资相差较多,
这样导致平均数与中位数(众数)偏差较大(平均数受极端值影响较大),
所以平均数不能反映这个公司员工的工资水平.
解后反思
众数、中位数和平均数的比较
名称 优点 缺点
平均数 与中位数相比,平均数反映出样本数据中更多的信息,对样本中的极端值更加敏感 样本中的任何一个数据的改变都会引起平均数的改变.数据越“离群”,对平均数的影响越大
中位数 不受少数几个极端数据(即排序靠前或靠后的数据)的影响 对极端值不敏感
众数 体现了样本数据的最大集中点 只能传递数据中一部分信息,对极端值不敏感
7.C 题图1是对称的,所以平均数=中位数=众数,故A中判断正确;
题图2中众数最小,“右拖尾”表现为平均数大于中位数,故B中判断正确,C中判断错误;
题图3“左拖尾”表现为众数最大,平均数小于中位数,故D中判断正确.
故选C.
8.B 由题图知,支出在[40,50)内的小矩形最高,故估计众数为45元,A错;
支出在[50,60)内的频率为1-(0.01+0.024+0.036)×10=0.3,D错;
因为10×(0.01+0.024)=0.34<0.5,0.34+10×0.036=0.7,所以中位数在[40,50)内,设中位数为x元,则0.34+(x-40)×0.036=0.5,解得x=,故中位数是元,B正确;
平均数为10×(0.01×25+0.024×35+0.036×45)+0.3×55=43.6元,C错.
故选B.
9.B 由题中频率分布直方图可知众数为65,即b=65,
平均数为45×0.15+55×0.2+65×0.25+75×0.2+85×0.1+95×0.1=67,即c=67,
因为10×(0.015+0.020)=0.35<0.5,0.35+0.025×10=0.6>0.5,所以中位数位于区间[60,70),
则有0.35+(a-60)×0.025=0.5,解得a=66,
所以b
估计该市居民月均用水量不少于3 t的人数为(0.12+0.08+0.04)×0.5×60×104=72 000.
(2)由题图可估计该市居民月均用水量的众数为(2+2.5)÷2=2.25(t).设中位数为x t,
因为(0.08+0.16+0.3+0.42)×0.5=0.48<0.5,0.48+0.50×0.5=0.73>0.5,所以2
故估计该市居民月均用水量的中位数为2.04 t.
11.B 方差表示数据波动性的大小、稳定程度.数据越均数,方差越小,结合题图可知,B中数据主要集中在70~80内,且波动性小,故方差最小.
12.D 设数据x1,x2,…,xn的平均数和方差分别为和s2,则数据ax1+b,ax2+b,…,axn+b的平均数和方差分别为a+b和a2s2,所以y1,y2,…,y2 022的平均数为2×3+3=9,方差为22×56=224.故选D.
13.D 由题中折线图得到甲六次测试的成绩(单位:分)依次为90,93,92,94,96,93,
乙六次测试的成绩(单位:分)依次为93,94,91,95,92,93,
则甲的平均成绩为×(90+93+92+94+96+93)=93,
乙的平均成绩为×(93+94+91+95+92+93)=93,故A,B均错误;
甲成绩的极差为96-90=6,乙成绩的极差为95-91=4,故C错误;
甲成绩的方差=×[(-3)2+02+(-1)2+12+32+02]=,
乙成绩的方差=×[02+12+(-2)2+22+(-1)2+02]=,
因为>,所以乙的成绩比甲的成绩稳定,D正确.故选D.
14.D 按照分层随机抽样的方法从甲队中抽取10×=6人,从乙队中抽取10×=4人,
这10人答对题目的平均数为×(6×1+4×1.5)=1.2,
所以这10人答对题目的方差为×{6×[1+(1-1.2)2]+4×[0.4+(1.5-1.2)2]}=0.82.故选D.
解题模板 若一个总体划分为两层,各层抽取的样本量、样本平均数和样本方差分别为m,,;n,,.记总的样本平均数为,样本方差为s2,则=+;s2={m[+]+n[+]}.
15.答案 2
解析 由题意得数据x1,x2,…,x10的方差s2=-=3-12=2.
故答案为2.
解后反思 方差的计算公式有两种形式,即s2=(xi-)2和s2=-,可以根据题目条件灵活选择.
16.解析 (1)==100,==100,
==,==1.
(2)∵两台机床所加工的零件的直径的平均值相同,>,
∴乙机床加工的零件的质量更稳定.
能力提升练
1.AC 2.ABD 3.BCD
1.AC 依题意得(0.015+0.025+0.035+0.005+2a)×10=1,解得a=0.010.
∵最高小矩形底边中点的横坐标为75,
∴众数是75,故A正确;
设样本的71%分位数为x,∵10×(0.010+0.015+0.025)=0.5,0.5+10×0.035=0.85,∴0.5+(x-70)×0.035=0.71,解得x=76,故B错误;
平均值为45×0.1+55×0.15+65×0.25+75×0.35+85×0.1+95×0.05=68.5,故C正确;
样本中得分低于60分的占(0.010+0.015)×10×100%=25%,∴该校学生中得分低于60分的约占25%,故D错误.
故选AC.
2.ABD 设甲:x1,x2,…,x10,乙:y1,y2,…,y10,新数据为z1,z2,…,z20.
对于A,=(z1+z2+…+z20)=(10a+10a)=a,A正确;
对于B,设甲:1,2,…,10,乙:21,22,…,30,则甲、乙两组数据的极差均为9,但混合后数据的极差为29,B正确;
对于C,因为(++…+-10)=(++…+-10)=c,所以++…+=10c+10,++…+=10c+10,=,
所以新数据的方差为(++…++++…+-20)=(10c+10+10c+10-20)=c+,
因为+-2=+-2×=≥0,
所以新数据的方差一定不小于c,C错误;
对于D,不妨设x1≤x2≤…≤x10,y1≤y2≤…≤y10,则d==,
将混合后的数据按从小到大排列,
若x5≤y5,则x6≥y6,所以第10,11个数为y5和y6,
若x5>y5,则x6
故选ABD.
3.BCD 对于甲,中位数为4,极差为3,所以这7个数可以是4,4,4,4,4,4,7,则甲不符合题意;
对于乙,中位数为3,众数为5,所以这7个数从小到大排列后,第4个数是3,
所以1,2,3中一定有一个数出现2次,5出现3次,所以这7个数中一定没有出现7,则乙符合题意;
对于丙,若出现1个7,则这7个数从小到大排列后,后4个数之和最小为19,前3个数之和最小为3,从而这7个数的平均数最小为>3,即这7个数的平均数不可能为3,所以数据中不可能出现7,故丙符合题意;
对于丁,设这7个数分别为x1,x2,x3,x4,x5,x6,x7,则x1+x2+x3+x4+x5+x6+x7=21,
(x1-3)2+(x2-3)2+(x3-3)2+(x4-3)2+(x5-3)2+(x6-3)2+(x7-3)2=21,
若x1=7,则x2+x3+x4+x5+x6+x7=14,
(x2-3)2+(x3-3)2+(x4-3)2+(x5-3)2+(x6-3)2+(x7-3)2=5,
从而x2,x3,x4,x5,x6,x7这6个数可能是4,4,4,4,4,3或4,4,4,4,3,2或4,4,4,3,2,2或4,4,3,2,2,2或4,3,2,2,2,2或3,2,2,2,2,2或5,4,3,3,3,3或5,3,3,3,3,2或4,3,3,3,3,1或3,3,3,3,2,1,这与x2+x3+x4+x5+x6+x7=14矛盾,
即这7个数中一定没有出现7,故丁符合题意.
故选BCD.
4.答案 4;1.5
解析 由高中三个年级学生的总样本平均数为4.1,
可得=4.1,解得=4.
因为总样本方差为3.14,所以×[3.5+(5-4.1)2]+×[2+(4-4.1)2]+×[+(3-4.1)2]=3.14,
解得=1.5.
故答案为4;1.5.
5.答案 5
解析 设样本数据为a,b,c,d,且a
则(a-3)2+(b-3)2+(c-3)2+(d-3)2=10,
所以(d-3)2≤10,解得d≤+3.
当d=6时,(a-3)2+(b-3)2+(c-3)2=1,因为样本数据互不相同,所以不存在a,b,c使得等式成立.
当d=5时,(a-3)2+(b-3)2+(c-3)2=6,存在a=1,b=2,c=4,使得等式成立,故样本数据中的最大值为5.
6.解析 (1)由题中频率分布直方图知(0.01+m+0.04+0.02)×10=1,解得m=0.03.
设此次知识竞赛活动学生分数的中位数为x0,
因为数据落在[60,80)内的频率为0.4,落在[60,90)内的频率为0.8,所以80
故估计此次知识竞赛活动学生分数的中位数为82.5.
(2)由题中频率分布直方图及(1)知数据落在[60,70),[70,80),[80,90),[90,100]内的频率分别为0.1,0.3,0.4,0.2,则估计此次知识竞赛活动学生分数的平均数为65×0.1+75×0.3+85×0.4+95×0.2=82.
此次知识竞赛活动学生分数不低于82的频率为0.2+×0.4=0.52,
故估计参赛的500名学生中获奖的人数为500×0.52=260.
7.解析 (1)由题意可知,甲方案日薪y与送货单数n的函数关系式为y=n×1+100=n+100,n∈N.
对于乙方案,当n≤55,n∈N时,y=150;
当n>55,n∈N时,y=150+(n-55)×10=10n-400.
故乙方案日薪y与送货单数n的函数关系式为
y=
(2)①甲方案日薪X的平均数==155(元),
方差=×[2×(150-155)2+3×(154-155)2+2×(156-155)2+2×(158-155)2+(160-155)2]
=×(50+3+2+18+25)=9.8.
乙方案日薪X的平均数==163(元),
方差=×[2×(150-163)2+3×(150-163)2+2×(160-163)2+2×(180-163)2+(200-163)2]
=×(338+507+18+578+1 369)=281.
②答案一:由①可知<,则选择乙方案比较合适.
答案二:由①可知,<,二者相差不大,>,二者相差较大,即甲方案日薪波动情况比乙小得多,则选择甲方案比较合适.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
