2025人教A版高中数学必修第二册强化练习题--第九章 统计 复习提升
文档属性
| 名称 | 2025人教A版高中数学必修第二册强化练习题--第九章 统计 复习提升 |

|
|
| 格式 | docx | ||
| 文件大小 | 477.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 09:25:52 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025人教A版高中数学必修第二册
本章复习提升
易混易错练
易错点1 在分层随机抽样中忽视抽样比或者权重致错
1.(2024广东珠海第一中学月考)某校高一、高二、高三共有学生6 000名,为了解同学们的学习情况,计划采用样本量比例分配的分层随机抽样的方法从这6 000名学生中抽取一个容量为60的样本,若从高一、高二、高三抽取的人数恰好是从小到大排列的连续偶数,则该校高二年级的人数为( )
A.1 000 B.1 500
C.2 000 D.3 000
2.(2024湖南长沙雅礼中学月考)为调查某地区中学生每天的睡眠时间,采用样本量比例分配的分层随机抽样,现抽取初中生800人,其每天睡眠时间的均值为9 h,方差为1,抽取高中生1 200人,其每天睡眠时间的均值为8 h,方差为0.5,则估计该地区中学生每天睡眠时间的方差为( )
A.0.96 B.0.94
C.0.79 D.0.75
3.(2024四川成都期中)某地区从11 000名小学生、10 000名初中生和4 000名高中生中采用样本量比例分配的分层随机抽样方法抽取n名学生进行视力测试,若初中生比高中生多抽取60人,则n= .
易错点2 应用频率分布直方图解题时把纵坐标当成频率而致错
4.(2024福建宁德寿宁第一中学月考)某小区从2 000户居民中随机抽取100户进行月用电量调查,发现他们的月用电量都在50~350 kW·h范围内,进行适当分组后(每组为左闭右开的区间),画出频率分布直方图如图所示,则( )
A.小区月用电量的平均数为186.5,极差为300
B.小区月用电量的中位数为171,众数为175
C.可以估计小区居民月用电量的85%分位数为262.5
D.小区月用电量不低于250 kW·h的约有380户
5.(多选题)(2024浙江绍兴第一中学期中)在某市高三年级举行的一次模拟考试中,某学科共有20 000人参加考试.为了了解本次考试学生成绩情况,从中抽取了部分学生的成绩(成绩均为正整数,满分为100分)作为样本进行统计,样本容量为n,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图所示,其中,成绩落在区间[50,60)内的人数为16,则( )
A.图中x=0.016
B.样本容量n=1 000
C.估计该市全体学生成绩的平均数为71.6
D.该市要对成绩前25%的学生授予“优秀学生”称号,则授予“优秀学生”称号的学生的最低考试成绩大约为77.25分
6.某医疗科研所研发出A,B两种新配方中药,现从生产的这两种新配方中药产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于85的为废品,在[85,115)内的为一等品,大于或等于115的为特等品.现把测量数据整理如下,其中B配方中药的废品有6件.
A配方中药的频数分布表
质量 指标值 [75, 85) [85, 95) [95, 105) [105, 115) [115, 125]
频数 8 a 36 24 8
(1)求a,b的值;
(2)若从A,B两种新配方中药中选择一种进行推广,试确定推广哪种比较好.(同一组中的数据用该组区间的中点值作代表)
易错点3 对百分位数理解不到位致错
7.(多选题)(2024河南创新发展联盟月考)已知某省2023年各地市地区生产总值的占比如图所示,则下列结论正确的是( )
A.A市2023年地区生产总值比B市多
B.图中11个地市2023年地区生产总值占比数据的40%分位数为5.92%
C.图中11个地市2023年地区生产总值占比数据的70%分位数为4.58%
D.若该省2024年各地市地区生产总值的增长率相等,则该省2024年各地市地区生产总值的占比不变
8.(多选题)(2024辽宁辽阳期末)某人记录了自己一周内每天的运动时长(单位:min):54,58,46,62,80,50,x.若这组数据的第40百分位数与第20百分位数的差为3,则x的值可能为( )
A.47 B.45 C.53 D.60
9.(2024黑龙江大庆实验中学月考)已知互不相等的4个正整数从小到大排列为a1,a2,a3,a4.若它们的和为12,且这4个数据的极差是中位数的2倍,求这4个数据的第75百分位数.
思想方法练
一、数形结合思想在统计中的应用
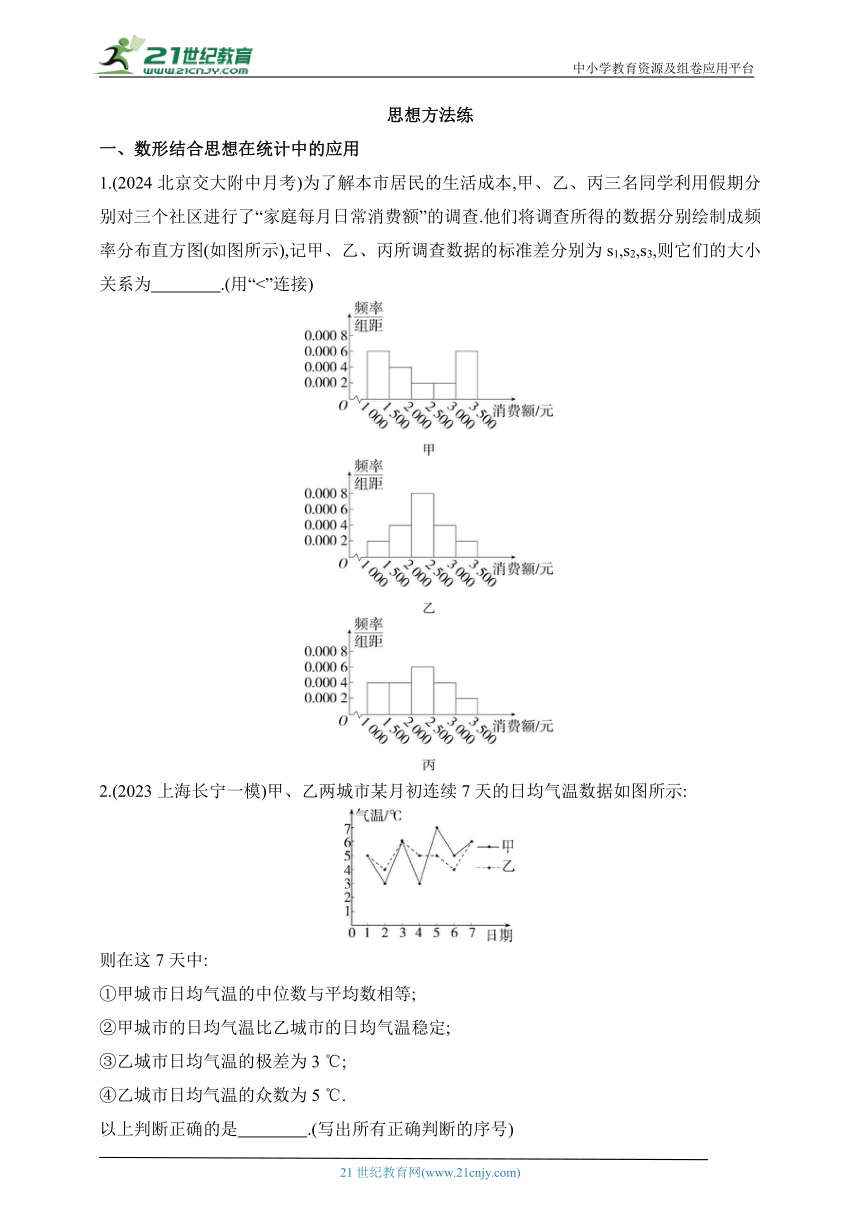
1.(2024北京交大附中月考)为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为s1,s2,s3,则它们的大小关系为 .(用“<”连接)
2.(2023上海长宁一模)甲、乙两城市某月初连续7天的日均气温数据如图所示:
则在这7天中:
①甲城市日均气温的中位数与平均数相等;
②甲城市的日均气温比乙城市的日均气温稳定;
③乙城市日均气温的极差为3 ℃;
④乙城市日均气温的众数为5 ℃.
以上判断正确的是 .(写出所有正确判断的序号)
二、函数与方程思想在统计中的应用
3.(2023广东河源期末)某校为了了解高三年级学生的身体素质状况,在开学初举行了一场身体素质体能测试,以便对体能不达标的学生进行针对性的训练,促进他们体能的提升.现从整个年级测试成绩中抽取100名学生的测试成绩,并把测试成绩分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组,绘制成频率分布直方图(如图所示),其中[90,100]这一组对应的纵坐标为a,则该次体能测试成绩的80%分位数约为 分.
4.设样本数据x1,x2,…,x2 022的平均数为,方差为s2,若数据2(x1+1),2(x2+1),…,2(x2 022+1)的平均数比方差大4,求s2-的最大值.
答案与分层梯度式解析
本章复习提升
易混易错练
1.C 2.B 4.C 5.AD 7.ABD 8.AC
1.C 由题意可设高三抽取的人数为2a,则高二抽取的人数为2a-2,高一抽取的人数为2a-4,
因为样本容量为60,
所以2a+2a-2+2a-4=60,解得a=11,
设该校高二年级的人数为x,
根据分层随机抽样得=
易错点,解得x=2 000,故选C.
易错警示 解决有关分层随机抽样的问题时,先根据题目条件得出或计算出相应比例,或者各部分的权重,再列式求解.
2.B 初中生和高中生的权重分别为=和=易错点,则估计该地区中学生每天睡眠时间的均值为×9+×8=8.4(h),则估计该地区中学生每天睡眠时间的方差为×[1+(9-8.4)2]+×[0.5+(8-8.4)2]=0.94.
故选B.
3.答案 250
解析 设从小学生中抽取的人数为n1,从高中生中抽取的人数为n3,则从初中生中抽取的人数为n3+60,
所以==易错点,解得n3=40,n1=110,从而n=n1+n3+60+n3=250.
故答案为250.
4.C 对于A,小区月用电量的平均数为50×0.002 4×75+50×0.003 6
×125+50×0.006 0×175+50×0.004 4×225+50×0.002 4×275+50×
0.001 2×325=186,极差为300,故A错误;
对于B,小区月用电量的众数为=175,
因为50×(0.002 4+0.003 6)=0.3,50×(0.002 4+0.003 6+0.006 0)=0.6,
所以小区月用电量的中位数在[150,200)内,设中位数为m,
则0.3+(m-150)×0.006 0=0.5,解得m=,故B错误;
对于C,因为50×(0.002 4+0.003 6+0.006 0+0.004 4)=0.82<0.85,
50×(0.002 4+0.003 6+0.006 0+0.004 4+0.002 4)=0.94>0.85,
所以估计小区居民月用电量的85%分位数在[250,300)内,设为x,则0.82+(x-250)×0.002 4=0.85,解得x=262.5,故C正确;
对于D,样本中小区月用电量不低于250 kW·h的频率为0.002 4×50+0.001 2×50=0.18,
所以小区月用电量不低于250 kW·h的约有2 000×0.18=360户,故D错误.
故选C.
易错警示 利用频率分布直方图解决相关问题时,要注意纵坐标并不是频率,而是,频率分布直方图中小矩形的面积才是频率.
5.AD 对于A,由(x+0.030+0.040+0.010+0.004)×10=1,解得x=0.016,故A正确;
对于B,因为成绩落在区间[50,60)内的人数为16,
所以样本容量n=16÷(0.016×10)=100,故B不正确;
对于C,估计该市全体学生成绩的平均数为0.016×10×55+0.030×10×65+0.040×10×75+0.010×10×85+0.004×10×95=70.6,故C不正确;
对于D,设学生考试成绩的75%分位数为y分,
因为(0.016+0.030)×10=0.46<0.75,0.46+0.040×10=0.86>0.75,所以y∈[70,80),
则0.46+(y-70)×0.040=0.75,解得y=77.25,
所以最低考试成绩大约为77.25分的学生能被授予“优秀学生”称号,故D正确.
故选AD.
6.解析 (1)依题意,A,B两种新配方中药的样本容量相同,设为n,
因为B配方中药的废品有6件,所以=0.006×10,解得n=100,
则a=100-(8+36+24+8)=24.
由(0.006+b+0.038+0.022+0.008)×10=1,
解得b=0.026.
(2)A配方中药的质量指标值的平均数=×(80×8+90×24+100×36+110×24+120×8)=100,
方差=×[(-20)2×8+(-10)2×24+102×24+202×8]=112.
B配方中药的质量指标值的平均数=80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100,
方差=(-20)2×0.06+(-10)2×0.26+102×0.22+202×0.08=104.
综上,=,>,即两种新配方中药的质量指标值的平均数相等,但B配方中药的质量指标值比A配方中药的稳定,所以选择B配方中药进行推广比较好.
7.ABD A市2023年地区生产总值比B市多,故A正确;
因为11×40%=4.4,所以40%分位数为从小到大排列后的第5个数据
易错点,即为5.92%,故B正确;
因为11×70%=7.7,所以70%分位数为从小到大排列后的第8个数据
易错点,即为10.1%,故C错误;
若该省2024年各地市地区生产总值的增长率相等,则该省2024年各地市地区生产总值的占比不变,D正确.
故选ABD.
8.AC 将除x外的6个数据从小到大排列为46,50,54,58,62,80易错点.
7×20%=1.4,7×40%=2.8,
若x≤46,则这组数据的第20百分位数与第40百分位数分别是46和50,50-46≠3,不符合题意;
若x≥54,则这组数据的第20百分位数与第40百分位数分别是50和54,54-50≠3,不符合题意.
所以469.解析 这组数据的极差为a4-a1,中位数为,
由题意得a4-a1=2×=a2+a3,
即a4=a1+a2+a3,
又a1+a2+a3+a4=12,
所以2a4=12,解得a4=6,
则a1+a2+a3=6.
因为a1,a2,a3为正整数且互不相等,
所以a1=1,a2=2,a3=3.
因为75%×4=3,所以这4个数据的第75百分位数为a3和a4的平均数
易错点,即==.
易错警示 当计算n个数据的第p百分位数时,首先按从小到大排列原始数据,然后计算i=n×p%,若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据.
思想方法练
1.答案 s2解析 观察题中三个频率分布直方图,可得甲的数据绝大部分都处在两端,数据大多离平均数远,表现得最分散,所以其标准差最大;乙的数据绝大部分都在平均数左右,数据最集中,所以其标准差最小;丙的数据分布均匀,数据偏离平均数的程度比甲低,集中程度比乙低,故其标准差介于甲、乙之间.故答案为s22.答案 ①④
解析 甲城市7天的日均气温分别为5 ℃,3 ℃,6 ℃,3 ℃,7 ℃,5 ℃,6 ℃;
乙城市7天的日均气温分别为5 ℃,4 ℃,6 ℃,5 ℃,5 ℃,4 ℃,6 ℃.
由题中折线图读出原始数据,进而利用相关公式得出中位数、平均数、众数、极差等,体现了数形结合思想.
对于①,甲城市日均气温的中位数为5 ℃,平均数为=5(℃),故①正确;
对于②,根据题中折线图知乙城市的日均气温更稳定,故②错误;
对于③,乙城市日均气温的极差为2 ℃,故③错误;
对于④,乙城市日均气温的众数为5 ℃,故④正确.
思想方法 数形结合思想是统计学中很重要的一种思想方法.一方面用图形可以直观表示相关统计量;另一方面可以借助图形分析样本数据的分布状况、变化趋势、变量间的关系等,进而估计总体的状况.常见的统计图有条形图、扇形图、折线图、频率分布直方图等,要熟练掌握它们的特点.
3.答案 92
解析 根据频率分布直方图中小矩形的面积之和为1列方程.
由(0.002+0.004+0.014+0.020+0.035+a)×10=1,
解得a=0.025.
因为0.02+0.04+0.14+0.2+0.35=0.75,
所以该次体能测试成绩的80%分位数落在[90,100]内,设80%分位数为x分,
根据百分位数的定义列方程.
则(x-90)×0.025=0.8-0.75,解得x=92.
4.解析 根据平均数和方差的性质,可得数据2(x1+1),2(x2+1),…,
2(x2 022+1)的平均数为2(+1),方差为22s2=4s2.
根据题意列式,将s2-转化为关于的一元二次函数,利用二次函数的性质求最值.
由题意得,2(+1)-4s2=4,即s2=-,
则s2-=--=--.
利用方差的性质求的取值范围.
因为s2≥0,所以-≥0,即≥1,
故当=1时,s2-取得最大值,最大值是-1.
思想方法 在统计中,利用相关计算公式列出方程(组),进而解决统计问题是一种最基本的方法.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教A版高中数学必修第二册
本章复习提升
易混易错练
易错点1 在分层随机抽样中忽视抽样比或者权重致错
1.(2024广东珠海第一中学月考)某校高一、高二、高三共有学生6 000名,为了解同学们的学习情况,计划采用样本量比例分配的分层随机抽样的方法从这6 000名学生中抽取一个容量为60的样本,若从高一、高二、高三抽取的人数恰好是从小到大排列的连续偶数,则该校高二年级的人数为( )
A.1 000 B.1 500
C.2 000 D.3 000
2.(2024湖南长沙雅礼中学月考)为调查某地区中学生每天的睡眠时间,采用样本量比例分配的分层随机抽样,现抽取初中生800人,其每天睡眠时间的均值为9 h,方差为1,抽取高中生1 200人,其每天睡眠时间的均值为8 h,方差为0.5,则估计该地区中学生每天睡眠时间的方差为( )
A.0.96 B.0.94
C.0.79 D.0.75
3.(2024四川成都期中)某地区从11 000名小学生、10 000名初中生和4 000名高中生中采用样本量比例分配的分层随机抽样方法抽取n名学生进行视力测试,若初中生比高中生多抽取60人,则n= .
易错点2 应用频率分布直方图解题时把纵坐标当成频率而致错
4.(2024福建宁德寿宁第一中学月考)某小区从2 000户居民中随机抽取100户进行月用电量调查,发现他们的月用电量都在50~350 kW·h范围内,进行适当分组后(每组为左闭右开的区间),画出频率分布直方图如图所示,则( )
A.小区月用电量的平均数为186.5,极差为300
B.小区月用电量的中位数为171,众数为175
C.可以估计小区居民月用电量的85%分位数为262.5
D.小区月用电量不低于250 kW·h的约有380户
5.(多选题)(2024浙江绍兴第一中学期中)在某市高三年级举行的一次模拟考试中,某学科共有20 000人参加考试.为了了解本次考试学生成绩情况,从中抽取了部分学生的成绩(成绩均为正整数,满分为100分)作为样本进行统计,样本容量为n,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图所示,其中,成绩落在区间[50,60)内的人数为16,则( )
A.图中x=0.016
B.样本容量n=1 000
C.估计该市全体学生成绩的平均数为71.6
D.该市要对成绩前25%的学生授予“优秀学生”称号,则授予“优秀学生”称号的学生的最低考试成绩大约为77.25分
6.某医疗科研所研发出A,B两种新配方中药,现从生产的这两种新配方中药产品中随机抽取数量相同的样本,测量这些产品的质量指标值,规定指标值小于85的为废品,在[85,115)内的为一等品,大于或等于115的为特等品.现把测量数据整理如下,其中B配方中药的废品有6件.
A配方中药的频数分布表
质量 指标值 [75, 85) [85, 95) [95, 105) [105, 115) [115, 125]
频数 8 a 36 24 8
(1)求a,b的值;
(2)若从A,B两种新配方中药中选择一种进行推广,试确定推广哪种比较好.(同一组中的数据用该组区间的中点值作代表)
易错点3 对百分位数理解不到位致错
7.(多选题)(2024河南创新发展联盟月考)已知某省2023年各地市地区生产总值的占比如图所示,则下列结论正确的是( )
A.A市2023年地区生产总值比B市多
B.图中11个地市2023年地区生产总值占比数据的40%分位数为5.92%
C.图中11个地市2023年地区生产总值占比数据的70%分位数为4.58%
D.若该省2024年各地市地区生产总值的增长率相等,则该省2024年各地市地区生产总值的占比不变
8.(多选题)(2024辽宁辽阳期末)某人记录了自己一周内每天的运动时长(单位:min):54,58,46,62,80,50,x.若这组数据的第40百分位数与第20百分位数的差为3,则x的值可能为( )
A.47 B.45 C.53 D.60
9.(2024黑龙江大庆实验中学月考)已知互不相等的4个正整数从小到大排列为a1,a2,a3,a4.若它们的和为12,且这4个数据的极差是中位数的2倍,求这4个数据的第75百分位数.
思想方法练
一、数形结合思想在统计中的应用
1.(2024北京交大附中月考)为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为s1,s2,s3,则它们的大小关系为 .(用“<”连接)
2.(2023上海长宁一模)甲、乙两城市某月初连续7天的日均气温数据如图所示:
则在这7天中:
①甲城市日均气温的中位数与平均数相等;
②甲城市的日均气温比乙城市的日均气温稳定;
③乙城市日均气温的极差为3 ℃;
④乙城市日均气温的众数为5 ℃.
以上判断正确的是 .(写出所有正确判断的序号)
二、函数与方程思想在统计中的应用
3.(2023广东河源期末)某校为了了解高三年级学生的身体素质状况,在开学初举行了一场身体素质体能测试,以便对体能不达标的学生进行针对性的训练,促进他们体能的提升.现从整个年级测试成绩中抽取100名学生的测试成绩,并把测试成绩分成[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]六组,绘制成频率分布直方图(如图所示),其中[90,100]这一组对应的纵坐标为a,则该次体能测试成绩的80%分位数约为 分.
4.设样本数据x1,x2,…,x2 022的平均数为,方差为s2,若数据2(x1+1),2(x2+1),…,2(x2 022+1)的平均数比方差大4,求s2-的最大值.
答案与分层梯度式解析
本章复习提升
易混易错练
1.C 2.B 4.C 5.AD 7.ABD 8.AC
1.C 由题意可设高三抽取的人数为2a,则高二抽取的人数为2a-2,高一抽取的人数为2a-4,
因为样本容量为60,
所以2a+2a-2+2a-4=60,解得a=11,
设该校高二年级的人数为x,
根据分层随机抽样得=
易错点,解得x=2 000,故选C.
易错警示 解决有关分层随机抽样的问题时,先根据题目条件得出或计算出相应比例,或者各部分的权重,再列式求解.
2.B 初中生和高中生的权重分别为=和=易错点,则估计该地区中学生每天睡眠时间的均值为×9+×8=8.4(h),则估计该地区中学生每天睡眠时间的方差为×[1+(9-8.4)2]+×[0.5+(8-8.4)2]=0.94.
故选B.
3.答案 250
解析 设从小学生中抽取的人数为n1,从高中生中抽取的人数为n3,则从初中生中抽取的人数为n3+60,
所以==易错点,解得n3=40,n1=110,从而n=n1+n3+60+n3=250.
故答案为250.
4.C 对于A,小区月用电量的平均数为50×0.002 4×75+50×0.003 6
×125+50×0.006 0×175+50×0.004 4×225+50×0.002 4×275+50×
0.001 2×325=186,极差为300,故A错误;
对于B,小区月用电量的众数为=175,
因为50×(0.002 4+0.003 6)=0.3,50×(0.002 4+0.003 6+0.006 0)=0.6,
所以小区月用电量的中位数在[150,200)内,设中位数为m,
则0.3+(m-150)×0.006 0=0.5,解得m=,故B错误;
对于C,因为50×(0.002 4+0.003 6+0.006 0+0.004 4)=0.82<0.85,
50×(0.002 4+0.003 6+0.006 0+0.004 4+0.002 4)=0.94>0.85,
所以估计小区居民月用电量的85%分位数在[250,300)内,设为x,则0.82+(x-250)×0.002 4=0.85,解得x=262.5,故C正确;
对于D,样本中小区月用电量不低于250 kW·h的频率为0.002 4×50+0.001 2×50=0.18,
所以小区月用电量不低于250 kW·h的约有2 000×0.18=360户,故D错误.
故选C.
易错警示 利用频率分布直方图解决相关问题时,要注意纵坐标并不是频率,而是,频率分布直方图中小矩形的面积才是频率.
5.AD 对于A,由(x+0.030+0.040+0.010+0.004)×10=1,解得x=0.016,故A正确;
对于B,因为成绩落在区间[50,60)内的人数为16,
所以样本容量n=16÷(0.016×10)=100,故B不正确;
对于C,估计该市全体学生成绩的平均数为0.016×10×55+0.030×10×65+0.040×10×75+0.010×10×85+0.004×10×95=70.6,故C不正确;
对于D,设学生考试成绩的75%分位数为y分,
因为(0.016+0.030)×10=0.46<0.75,0.46+0.040×10=0.86>0.75,所以y∈[70,80),
则0.46+(y-70)×0.040=0.75,解得y=77.25,
所以最低考试成绩大约为77.25分的学生能被授予“优秀学生”称号,故D正确.
故选AD.
6.解析 (1)依题意,A,B两种新配方中药的样本容量相同,设为n,
因为B配方中药的废品有6件,所以=0.006×10,解得n=100,
则a=100-(8+36+24+8)=24.
由(0.006+b+0.038+0.022+0.008)×10=1,
解得b=0.026.
(2)A配方中药的质量指标值的平均数=×(80×8+90×24+100×36+110×24+120×8)=100,
方差=×[(-20)2×8+(-10)2×24+102×24+202×8]=112.
B配方中药的质量指标值的平均数=80×0.06+90×0.26+100×0.38+110×0.22+120×0.08=100,
方差=(-20)2×0.06+(-10)2×0.26+102×0.22+202×0.08=104.
综上,=,>,即两种新配方中药的质量指标值的平均数相等,但B配方中药的质量指标值比A配方中药的稳定,所以选择B配方中药进行推广比较好.
7.ABD A市2023年地区生产总值比B市多,故A正确;
因为11×40%=4.4,所以40%分位数为从小到大排列后的第5个数据
易错点,即为5.92%,故B正确;
因为11×70%=7.7,所以70%分位数为从小到大排列后的第8个数据
易错点,即为10.1%,故C错误;
若该省2024年各地市地区生产总值的增长率相等,则该省2024年各地市地区生产总值的占比不变,D正确.
故选ABD.
8.AC 将除x外的6个数据从小到大排列为46,50,54,58,62,80易错点.
7×20%=1.4,7×40%=2.8,
若x≤46,则这组数据的第20百分位数与第40百分位数分别是46和50,50-46≠3,不符合题意;
若x≥54,则这组数据的第20百分位数与第40百分位数分别是50和54,54-50≠3,不符合题意.
所以46
由题意得a4-a1=2×=a2+a3,
即a4=a1+a2+a3,
又a1+a2+a3+a4=12,
所以2a4=12,解得a4=6,
则a1+a2+a3=6.
因为a1,a2,a3为正整数且互不相等,
所以a1=1,a2=2,a3=3.
因为75%×4=3,所以这4个数据的第75百分位数为a3和a4的平均数
易错点,即==.
易错警示 当计算n个数据的第p百分位数时,首先按从小到大排列原始数据,然后计算i=n×p%,若i是整数,则第p百分位数为第i项与第(i+1)项数据的平均数,若i不是整数,而大于i的比邻整数为j,则第p百分位数为第j项数据.
思想方法练
1.答案 s2
解析 甲城市7天的日均气温分别为5 ℃,3 ℃,6 ℃,3 ℃,7 ℃,5 ℃,6 ℃;
乙城市7天的日均气温分别为5 ℃,4 ℃,6 ℃,5 ℃,5 ℃,4 ℃,6 ℃.
由题中折线图读出原始数据,进而利用相关公式得出中位数、平均数、众数、极差等,体现了数形结合思想.
对于①,甲城市日均气温的中位数为5 ℃,平均数为=5(℃),故①正确;
对于②,根据题中折线图知乙城市的日均气温更稳定,故②错误;
对于③,乙城市日均气温的极差为2 ℃,故③错误;
对于④,乙城市日均气温的众数为5 ℃,故④正确.
思想方法 数形结合思想是统计学中很重要的一种思想方法.一方面用图形可以直观表示相关统计量;另一方面可以借助图形分析样本数据的分布状况、变化趋势、变量间的关系等,进而估计总体的状况.常见的统计图有条形图、扇形图、折线图、频率分布直方图等,要熟练掌握它们的特点.
3.答案 92
解析 根据频率分布直方图中小矩形的面积之和为1列方程.
由(0.002+0.004+0.014+0.020+0.035+a)×10=1,
解得a=0.025.
因为0.02+0.04+0.14+0.2+0.35=0.75,
所以该次体能测试成绩的80%分位数落在[90,100]内,设80%分位数为x分,
根据百分位数的定义列方程.
则(x-90)×0.025=0.8-0.75,解得x=92.
4.解析 根据平均数和方差的性质,可得数据2(x1+1),2(x2+1),…,
2(x2 022+1)的平均数为2(+1),方差为22s2=4s2.
根据题意列式,将s2-转化为关于的一元二次函数,利用二次函数的性质求最值.
由题意得,2(+1)-4s2=4,即s2=-,
则s2-=--=--.
利用方差的性质求的取值范围.
因为s2≥0,所以-≥0,即≥1,
故当=1时,s2-取得最大值,最大值是-1.
思想方法 在统计中,利用相关计算公式列出方程(组),进而解决统计问题是一种最基本的方法.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
