2025北师大版高中数学必修第二册强化练习题--专题强化练10 空间角的有关计算
文档属性
| 名称 | 2025北师大版高中数学必修第二册强化练习题--专题强化练10 空间角的有关计算 |
|
|
| 格式 | docx | ||
| 文件大小 | 443.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025北师大版高中数学必修第二册
专题强化练10 空间角的有关计算
1.(2023浙江杭州源清中学期末)如图,在正三棱柱ABC-A1B1C1中,AA1=3,AB=2,则异面直线A1B与B1C夹角的余弦值为( )
A.
2.(2023甘肃武威联考)在正四棱柱ABCD-A1B1C1D1中,E是B1C1的中点,AB=2,AA1=,则BE与平面BB1D1D夹角的正弦值为( )
A.
3.(2023河北模拟预测)下图是延安革命纪念馆陈列的一个正四棱台形状的木盒子,它是以前计量粮食用的斗,纪念馆测得该正四棱台(每个面的厚度忽略不计)的下底面边长为38厘米,上底面边长为32厘米,侧棱长为23厘米,则斗的侧面与底面夹角的余弦值为( )
A.
4.(2024河南封丘一中月考)如图,甲站在水库底面上的点D处,乙站在水坝斜面上的点C处,测得从D,C到水库底面与水坝斜面的交线AB的距离分别为DA=5 m,CB=5 m,又测得AB的长为5 m,CD的长为5 m,则水库底面与水坝斜面所成的二面角的大小为 .
5.(2023江苏G4联盟联考)如图,在轴截面为正方形ABCD的圆柱中,M,N分别为弧的中点,且在平面ABCD的两侧.
(1)求证:四边形ANCM是矩形;
(2)求二面角B-MN-C的平面角的余弦值.
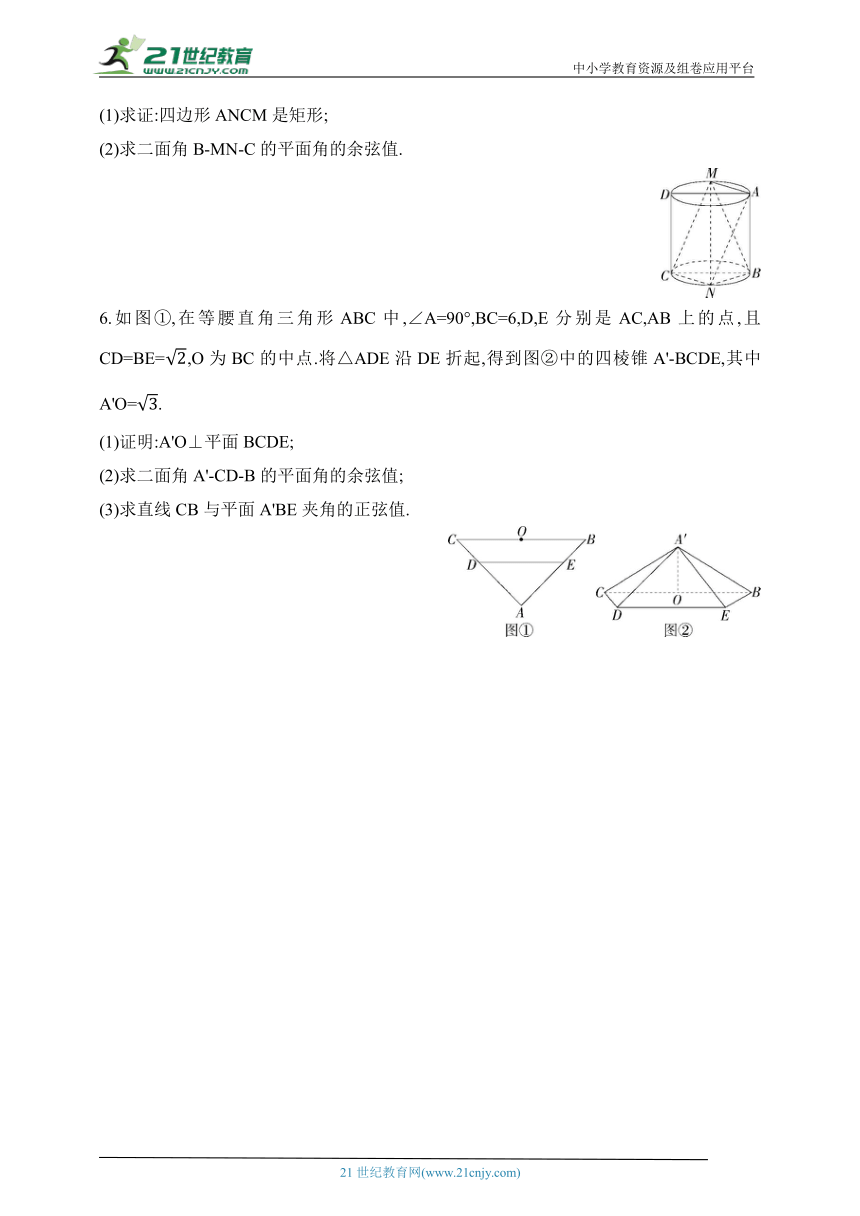
6.如图①,在等腰直角三角形ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,且CD=BE=,O为BC的中点.将△ADE沿DE折起,得到图②中的四棱锥A'-BCDE,其中A'O=.
(1)证明:A'O⊥平面BCDE;
(2)求二面角A'-CD-B的平面角的余弦值;
(3)求直线CB与平面A'BE夹角的正弦值.
答案与分层梯度式解析
专题强化练10 空间角的有关计算
1.A 如图所示,
连接BC1交B1C于点E,取A1C1的中点D,连接DE,B1D,
易知E为BC1的中点,所以DE∥A1B 且DE=A1B,则∠DEB1(或其补角)为异面直线A1B与B1C的夹角.
易得A1B=B1C=,则DE=B1E=,又B1D=,
故在△DB1E中,cos∠DEB1=.
2.A 如图所示,连接A1C1,交B1D1于点O,
易得DD1⊥平面A1B1C1D1,OC1 平面A1B1C1D1,
所以DD1⊥OC1,
又B1D1⊥OC1,B1D1∩DD1=D1,B1D1,DD1 平面BB1D1D,
所以OC1⊥平面BB1D1D,
取OB1的中点H,连接EH,易得EH∥OC1,
所以EH⊥平面BB1D1D,连接BH,
则∠HBE为BE与平面BB1D1D的夹角.
因为AB=2,AA1=,
所以EH=,
所以sin∠HBE=.
3.A 如图,在正四棱台ABCD-A1B1C1D1中,设上、下底面的中心分别为O1,O,B1C1,BC的中点分别为E,H,连接EH,O1E,OH,OO1,过E作EF⊥OH,垂足为F,
易得O1E∥OH,所以O,H,E,O1四点共面.
因为侧面BB1C1C为等腰梯形,所以EH⊥BC,
易得OH⊥BC,
因为EH∩OH=H,EH,OH 平面OHEO1,
所以BC⊥平面OHEO1,
又EH 平面BB1C1C,OH 平面ABCD,
所以∠EHF即为侧面BB1C1C与底面ABCD所成二面角的平面角,
即∠EHF即为斗的侧面与底面的夹角,
由题意可知O1E=16,OH=19,所以FH=19-16=3,
在等腰梯形BCC1B1中,BB1=23,则EH=,
在Rt△EFH中,cos∠EHF=,
所以斗的侧面与底面夹角的余弦值为.
故选A.
4.答案
解析 如图,过点B作BE∥AD且BE=AD,连接DE.
因为AD⊥AB,所以四边形ABED是矩形,
所以BE⊥AB,又BC⊥AB,所以∠CBE是所求二面角的平面角.
因为DE∥AB,BC⊥AB,
所以BC⊥DE,
又BE⊥DE,BC∩BE=B,BC,BE 平面BCE,
所以DE⊥平面BCE,
又CE 平面BCE,所以DE⊥CE,即∠DEC=90°,
因为四边形ABED是矩形,
所以AB=DE=5 m,BE=AD=5 m,
故在Rt△DEC中,CE=(m),
在△CBE中,由余弦定理得cos∠CBE=,
又0<∠CBE<π,所以∠CBE=,
故水库底面与水坝斜面所成的二面角的大小为.
5.解析 (1)证明:设正方形ABCD的边长为2a,取弧的中点Q,使Q与M同在平面ABCD的一侧,连接MQ,BQ,CQ,NQ,
则BC与NQ互相垂直平分,且BC=NQ=2a,
所以四边形BNCQ为正方形,BQ=NC=a,
因为M为弧的中点,所以MQ AB,
所以四边形ABQM为平行四边形,
所以AM BQ,所以AM CN,
所以四边形ANCM为平行四边形,
又AN=a,
所以AM2+AN2=MN2,所以AM⊥AN,
所以四边形ANCM是矩形.
(2)由(1)知,MB=MC=a,
所以MN2=MB2+BN2,MN2=MC2+CN2,
所以∠MBN=∠MCN=,
所以△MNB≌△MNC.
设Rt△MBN的斜边MN上的高为h,
则h=a,
作BP⊥MN于点P,连接CP,
因为∠BNP=∠CNP,BN=CN,PN=PN,
所以△BPN≌△CPN,
则∠CPN=∠BPN=90°,所以CP⊥MN,
则∠BPC即为二面角B-MN-C的平面角,
易得BP=CP=a,BC=2a,
在△BPC中,由余弦定理得cos∠BPC=,
由图可知,二面角B-MN-C的平面角为钝角,
所以二面角B-MN-C的平面角的余弦值为-.
6.解析 (1)证明:在题图①中连接OD,OE.
易得OC=3,AC=3.
在题图②中,连接OD,OE,
因为A'D=A'E=2,
所以A'D2=A'O2+OD2,A'E2=A'O2+OE2,
则A'O⊥OD,A'O⊥OE,
又OD∩OE=O,所以A'O⊥平面BCDE.
(2)在题图②中设CD,BE的延长线交于R点,取CR的中点M,连接OM,A'M,
则易证OM⊥CR,A'M⊥CR.
则∠A'MO就是二面角A'-CD-B的平面角,
因为A'O⊥平面BCDE,所以A'O⊥OM,
易得OM=,
所以cos∠A'MO=,
即二面角A'-CD-B的平面角的余弦值为.
(3)取BR的中点N,连接A'N和ON,过点O作OQ⊥A'N于Q,连接BQ,易得OQ⊥平面A'BE,
所以∠OBQ就是直线BC与平面A'BE的夹角.
易得OQ=,OB=3,所以sin∠OBQ=,
即直线CB与平面A'BE夹角的正弦值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025北师大版高中数学必修第二册
专题强化练10 空间角的有关计算
1.(2023浙江杭州源清中学期末)如图,在正三棱柱ABC-A1B1C1中,AA1=3,AB=2,则异面直线A1B与B1C夹角的余弦值为( )
A.
2.(2023甘肃武威联考)在正四棱柱ABCD-A1B1C1D1中,E是B1C1的中点,AB=2,AA1=,则BE与平面BB1D1D夹角的正弦值为( )
A.
3.(2023河北模拟预测)下图是延安革命纪念馆陈列的一个正四棱台形状的木盒子,它是以前计量粮食用的斗,纪念馆测得该正四棱台(每个面的厚度忽略不计)的下底面边长为38厘米,上底面边长为32厘米,侧棱长为23厘米,则斗的侧面与底面夹角的余弦值为( )
A.
4.(2024河南封丘一中月考)如图,甲站在水库底面上的点D处,乙站在水坝斜面上的点C处,测得从D,C到水库底面与水坝斜面的交线AB的距离分别为DA=5 m,CB=5 m,又测得AB的长为5 m,CD的长为5 m,则水库底面与水坝斜面所成的二面角的大小为 .
5.(2023江苏G4联盟联考)如图,在轴截面为正方形ABCD的圆柱中,M,N分别为弧的中点,且在平面ABCD的两侧.
(1)求证:四边形ANCM是矩形;
(2)求二面角B-MN-C的平面角的余弦值.
6.如图①,在等腰直角三角形ABC中,∠A=90°,BC=6,D,E分别是AC,AB上的点,且CD=BE=,O为BC的中点.将△ADE沿DE折起,得到图②中的四棱锥A'-BCDE,其中A'O=.
(1)证明:A'O⊥平面BCDE;
(2)求二面角A'-CD-B的平面角的余弦值;
(3)求直线CB与平面A'BE夹角的正弦值.
答案与分层梯度式解析
专题强化练10 空间角的有关计算
1.A 如图所示,
连接BC1交B1C于点E,取A1C1的中点D,连接DE,B1D,
易知E为BC1的中点,所以DE∥A1B 且DE=A1B,则∠DEB1(或其补角)为异面直线A1B与B1C的夹角.
易得A1B=B1C=,则DE=B1E=,又B1D=,
故在△DB1E中,cos∠DEB1=.
2.A 如图所示,连接A1C1,交B1D1于点O,
易得DD1⊥平面A1B1C1D1,OC1 平面A1B1C1D1,
所以DD1⊥OC1,
又B1D1⊥OC1,B1D1∩DD1=D1,B1D1,DD1 平面BB1D1D,
所以OC1⊥平面BB1D1D,
取OB1的中点H,连接EH,易得EH∥OC1,
所以EH⊥平面BB1D1D,连接BH,
则∠HBE为BE与平面BB1D1D的夹角.
因为AB=2,AA1=,
所以EH=,
所以sin∠HBE=.
3.A 如图,在正四棱台ABCD-A1B1C1D1中,设上、下底面的中心分别为O1,O,B1C1,BC的中点分别为E,H,连接EH,O1E,OH,OO1,过E作EF⊥OH,垂足为F,
易得O1E∥OH,所以O,H,E,O1四点共面.
因为侧面BB1C1C为等腰梯形,所以EH⊥BC,
易得OH⊥BC,
因为EH∩OH=H,EH,OH 平面OHEO1,
所以BC⊥平面OHEO1,
又EH 平面BB1C1C,OH 平面ABCD,
所以∠EHF即为侧面BB1C1C与底面ABCD所成二面角的平面角,
即∠EHF即为斗的侧面与底面的夹角,
由题意可知O1E=16,OH=19,所以FH=19-16=3,
在等腰梯形BCC1B1中,BB1=23,则EH=,
在Rt△EFH中,cos∠EHF=,
所以斗的侧面与底面夹角的余弦值为.
故选A.
4.答案
解析 如图,过点B作BE∥AD且BE=AD,连接DE.
因为AD⊥AB,所以四边形ABED是矩形,
所以BE⊥AB,又BC⊥AB,所以∠CBE是所求二面角的平面角.
因为DE∥AB,BC⊥AB,
所以BC⊥DE,
又BE⊥DE,BC∩BE=B,BC,BE 平面BCE,
所以DE⊥平面BCE,
又CE 平面BCE,所以DE⊥CE,即∠DEC=90°,
因为四边形ABED是矩形,
所以AB=DE=5 m,BE=AD=5 m,
故在Rt△DEC中,CE=(m),
在△CBE中,由余弦定理得cos∠CBE=,
又0<∠CBE<π,所以∠CBE=,
故水库底面与水坝斜面所成的二面角的大小为.
5.解析 (1)证明:设正方形ABCD的边长为2a,取弧的中点Q,使Q与M同在平面ABCD的一侧,连接MQ,BQ,CQ,NQ,
则BC与NQ互相垂直平分,且BC=NQ=2a,
所以四边形BNCQ为正方形,BQ=NC=a,
因为M为弧的中点,所以MQ AB,
所以四边形ABQM为平行四边形,
所以AM BQ,所以AM CN,
所以四边形ANCM为平行四边形,
又AN=a,
所以AM2+AN2=MN2,所以AM⊥AN,
所以四边形ANCM是矩形.
(2)由(1)知,MB=MC=a,
所以MN2=MB2+BN2,MN2=MC2+CN2,
所以∠MBN=∠MCN=,
所以△MNB≌△MNC.
设Rt△MBN的斜边MN上的高为h,
则h=a,
作BP⊥MN于点P,连接CP,
因为∠BNP=∠CNP,BN=CN,PN=PN,
所以△BPN≌△CPN,
则∠CPN=∠BPN=90°,所以CP⊥MN,
则∠BPC即为二面角B-MN-C的平面角,
易得BP=CP=a,BC=2a,
在△BPC中,由余弦定理得cos∠BPC=,
由图可知,二面角B-MN-C的平面角为钝角,
所以二面角B-MN-C的平面角的余弦值为-.
6.解析 (1)证明:在题图①中连接OD,OE.
易得OC=3,AC=3.
在题图②中,连接OD,OE,
因为A'D=A'E=2,
所以A'D2=A'O2+OD2,A'E2=A'O2+OE2,
则A'O⊥OD,A'O⊥OE,
又OD∩OE=O,所以A'O⊥平面BCDE.
(2)在题图②中设CD,BE的延长线交于R点,取CR的中点M,连接OM,A'M,
则易证OM⊥CR,A'M⊥CR.
则∠A'MO就是二面角A'-CD-B的平面角,
因为A'O⊥平面BCDE,所以A'O⊥OM,
易得OM=,
所以cos∠A'MO=,
即二面角A'-CD-B的平面角的余弦值为.
(3)取BR的中点N,连接A'N和ON,过点O作OQ⊥A'N于Q,连接BQ,易得OQ⊥平面A'BE,
所以∠OBQ就是直线BC与平面A'BE的夹角.
易得OQ=,OB=3,所以sin∠OBQ=,
即直线CB与平面A'BE夹角的正弦值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
