13.3.2等边三角形的性质与判定 课件(共25张PPT)
文档属性
| 名称 | 13.3.2等边三角形的性质与判定 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-21 17:07:41 | ||
图片预览







文档简介
(共25张PPT)
人教版 八年级数学上
13.3.2等边三角形
---性质与判定
学习目标
1.微环境探索等边三角形的性质和判定.(重点)
2.能灵活运用等边三角形的性质和判定进行有关计算和证明.
(难点)
温故知新
等边对等角
三线合一
等角对等边
两边相等
1、说一说,什么样的三角形是等腰三角形?
轴对称图形
A
B
C
有两条边相等的三角形叫做等腰三角形
2、想一想,等腰三角形的性质有哪些?
3、想一想,等腰三角形的判定有哪些?
合作探究
等腰三角形
等边三角形
一般三角形
我们知道,等边三角形是三边都相等
的特殊的等腰三角形。
等边三角形除了三边相等之外,还有哪些性质?下面我们一起探究!
合作探究
A
B
C
A
B
C
思考1: 等边三角形的三个内角之间有什么关系?
等腰三角形
∠B=∠C
等边三角形
∠A=∠B=∠C
=60°
我们能推理证明吗?
合作探究
证明:∵ △ABC 是等边三角形,
∴ BC =AC,BC =AB.
∴ ∠A =∠B,∠A =∠C .
∴ ∠A =∠B =∠C .
∵ ∠A +∠B +∠C =180°,
∴ ∠A =60°.
∴ ∠A =∠B =∠C =60°.
已知:△ABC 是等边三角形
求证:∠A =∠B =∠C=60°.
A
B
C
合作探究
A
B
C
A
B
C
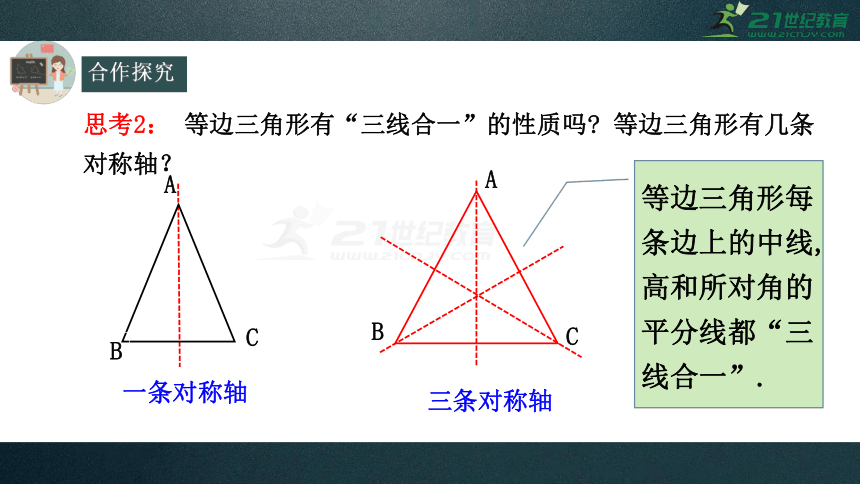
思考2: 等边三角形有“三线合一”的性质吗 等边三角形有几条对称轴?
一条对称轴
三条对称轴
等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
合作探究
图形 等腰三角形
性 质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60
两条边相等
三条边都相等
对比归纳;
小试牛刀
1.如图,△ABC是等边三角形的边长是4,BD平分∠ABC,点D在BC的延长线上,且∠E=30°,则CE的长( )
A.4 B.3 C.2 D.1
C
2.如图,△ABC是等边三角形,两个锐角都是45°的三角尺的一条直角边在AC上,则∠1
的度数为 。
A
C
B
150°
1
合作探究
议一议:一个三角形的边、角满足什么条件才是等边三角形?
图形 等腰三角形
判 定
三个角都相等的三角形是等边三角形
等边三角形
从角看:两个角相等的三角形是等腰三角形
从边看:两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
第三个判定方法:有一个角是60°的等腰三角形是等边三角形.
想一想:两条边相等且有一个角是60°的三角形也是等边三角形,对吗
典例精练
例 如图,在等边三角形ABC中,DE∥BC,求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ DE//BC,
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
想一想:本题还有其他证法吗?
一题多变
若点D、E 在边AB、AC 的反向延长线上,且DE∥BC,结论依然
成立吗?
证明: ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C
∵ DE∥BC,∴ ∠B =∠D,∠C =∠E.
∴ ∠EAD =∠D =∠E.
∴ △ADE 是等边三角形.
A
D
E
B
C
一题多变
上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗 试说明理由.
证明:
∵ △ABC是等边三角形,
∴ ∠A= 60°
∵ AD=AE
∴ △ADE是等腰三角形
∴ △ADE是等边三角形.
A
C
B
D
E
小试牛刀
1.下列三角形:①有两个角等于60°的三角形;②有一个角等于
60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相
等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形。其
中是等边三角形的有( )
A.①②③ B. ②③④ C. ①②④ D. ①②③④
D
2.等边三角形的两条高线相交成钝角的度数是( )
A.105° B.120° C.135° D.150°
B
小试牛刀
3.在等边△ABC中,BD是AC边上的中线,且BD=BF,
则∠CDF的度数是( )
A.10° B.15° C.20° D.25°
4.如图,△ABC和△ADE都是等边三角形,已知
△ABC的周长为24cm,EC=2cm,则△ADE的周长
是 cm.
A
C
B
D
E
18
B
小试牛刀
5.如图,在△ABC中,DE是AC边上的垂直平分线,且分别交BC,AC与点D,E,∠B=60°,∠C=30°。求证:△ABD是等边三角形.
证明:∵DE垂直平分AC
∴AD=CD,
∴∠DAC=∠C=30°,
∵∠ADB是△ADC的外角
∴∠ADB= ∠DAC+ ∠C=60°
∵∠B=60°
∴△ABD是等边三角形.
A
D
E
C
B
课堂小结
今天我们收获了哪些知识?
(畅所欲言)
等边三角形的性质是什么?
2.你能说一说等边三角形与等腰三角形的区别和联系吗?
3.如何判定一个三角形是等边三角形呢?
实战演练
1.如图,在等边三角形ABC中AD⊥BC,点E为AD上一点,∠CED=55°,则∠ABE等于是( )
A.10° B.15° C.20° D.25 °
D
2.如图,四边形ABCD是正方形,以CD为一边作等边△CDE,连接BE,则∠BEC为______.
15°
B
D
C
E
A
A
B
E
D
C
实战演练
3.如图,在四边形ABCD中,AB=AD,CB=CD, ∠A=60°,点E为AD 上一点,连接BD,CE交于点F,CE∥AB
(1)判断△DEF的形状,并说明理由.
(2)若AD=12,CE=8,求CF的长.
证明:(1)△DEF是等边三角形,理由如下:
∵AB=AD,
∴∠ABD=∠ADB,
∵∠A=60°,
∴∠ABD=∠ADB=60°,
A
F
E
C
D
B
实战演练
3.如图,在四边形ABCD中,AB=AD,CB=CD, ∠A=60°,点E为AD 上一点,连接BD,CE交于点F,CE∥AB
(1)判断△DEF的形状,并说明理由.
(2)若AD=12,CE=8,求CF的长.
∵ CE∥AB ,
∴∠DEF=∠A=60°,
∴∠EFD=60°,
∴△DEF是等边三角形,
A
F
E
C
D
B
实战演练
3.如图,在四边形ABCD中,AB=AD,CB=CD, ∠A=60°,点E为AD 上一点,连接BD,CE交于点F,CE∥AB
(1)判断△DEF的形状,并说明理由.
(2)若AD=12,CE=8,求CF的长.
(2)连接AC,
∵AB=AD,∠A=60°,
∴△ABD是等边三角形,
∵ AB=AD,CB=CD,
∴AC垂直平分BD,
A
F
E
C
D
B
实战演练
3.如图,在四边形ABCD中,AB=AD,CB=CD, ∠A=60°,点E为AD 上一点,连接BD,CE交于点F,CE∥AB
(1)判断△DEF的形状,并说明理由.
(2)若AD=12,CE=8,求CF的长.
∴∠DAC=30°,
∵∠DEF=60°,
∴∠ECA=∠DEF-∠EAC=30°,
∴∠ECA=∠EAC,
∴AE=CE=8,
A
F
E
C
D
B
实战演练
3.如图,在四边形ABCD中,AB=AD,CB=CD, ∠A=60°,点E为AD 上一点,连接BD,CE交于点F,CE∥AB
(1)判断△DEF的形状,并说明理由.
(2)若AD=12,CE=8,求CF的长.
∴DE=AD-AE=12-8=4,
∵△DEF是等边三角形,
∴EF=ED=4,
∴CF=CE-EF=4.
A
F
E
C
D
B
课后作业
教材83页习题13.3第12、14题.
https://www.21cnjy.com/help/help_extract.php
人教版 八年级数学上
13.3.2等边三角形
---性质与判定
学习目标
1.微环境探索等边三角形的性质和判定.(重点)
2.能灵活运用等边三角形的性质和判定进行有关计算和证明.
(难点)
温故知新
等边对等角
三线合一
等角对等边
两边相等
1、说一说,什么样的三角形是等腰三角形?
轴对称图形
A
B
C
有两条边相等的三角形叫做等腰三角形
2、想一想,等腰三角形的性质有哪些?
3、想一想,等腰三角形的判定有哪些?
合作探究
等腰三角形
等边三角形
一般三角形
我们知道,等边三角形是三边都相等
的特殊的等腰三角形。
等边三角形除了三边相等之外,还有哪些性质?下面我们一起探究!
合作探究
A
B
C
A
B
C
思考1: 等边三角形的三个内角之间有什么关系?
等腰三角形
∠B=∠C
等边三角形
∠A=∠B=∠C
=60°
我们能推理证明吗?
合作探究
证明:∵ △ABC 是等边三角形,
∴ BC =AC,BC =AB.
∴ ∠A =∠B,∠A =∠C .
∴ ∠A =∠B =∠C .
∵ ∠A +∠B +∠C =180°,
∴ ∠A =60°.
∴ ∠A =∠B =∠C =60°.
已知:△ABC 是等边三角形
求证:∠A =∠B =∠C=60°.
A
B
C
合作探究
A
B
C
A
B
C
思考2: 等边三角形有“三线合一”的性质吗 等边三角形有几条对称轴?
一条对称轴
三条对称轴
等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
合作探究
图形 等腰三角形
性 质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60
两条边相等
三条边都相等
对比归纳;
小试牛刀
1.如图,△ABC是等边三角形的边长是4,BD平分∠ABC,点D在BC的延长线上,且∠E=30°,则CE的长( )
A.4 B.3 C.2 D.1
C
2.如图,△ABC是等边三角形,两个锐角都是45°的三角尺的一条直角边在AC上,则∠1
的度数为 。
A
C
B
150°
1
合作探究
议一议:一个三角形的边、角满足什么条件才是等边三角形?
图形 等腰三角形
判 定
三个角都相等的三角形是等边三角形
等边三角形
从角看:两个角相等的三角形是等腰三角形
从边看:两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
第三个判定方法:有一个角是60°的等腰三角形是等边三角形.
想一想:两条边相等且有一个角是60°的三角形也是等边三角形,对吗
典例精练
例 如图,在等边三角形ABC中,DE∥BC,求证:△ADE是等边三角形.
A
C
B
D
E
证明:
∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ DE//BC,
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
想一想:本题还有其他证法吗?
一题多变
若点D、E 在边AB、AC 的反向延长线上,且DE∥BC,结论依然
成立吗?
证明: ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C
∵ DE∥BC,∴ ∠B =∠D,∠C =∠E.
∴ ∠EAD =∠D =∠E.
∴ △ADE 是等边三角形.
A
D
E
B
C
一题多变
上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗 试说明理由.
证明:
∵ △ABC是等边三角形,
∴ ∠A= 60°
∵ AD=AE
∴ △ADE是等腰三角形
∴ △ADE是等边三角形.
A
C
B
D
E
小试牛刀
1.下列三角形:①有两个角等于60°的三角形;②有一个角等于
60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相
等的三角形;④一腰上的中线也是这条腰上的高的等腰三角形。其
中是等边三角形的有( )
A.①②③ B. ②③④ C. ①②④ D. ①②③④
D
2.等边三角形的两条高线相交成钝角的度数是( )
A.105° B.120° C.135° D.150°
B
小试牛刀
3.在等边△ABC中,BD是AC边上的中线,且BD=BF,
则∠CDF的度数是( )
A.10° B.15° C.20° D.25°
4.如图,△ABC和△ADE都是等边三角形,已知
△ABC的周长为24cm,EC=2cm,则△ADE的周长
是 cm.
A
C
B
D
E
18
B
小试牛刀
5.如图,在△ABC中,DE是AC边上的垂直平分线,且分别交BC,AC与点D,E,∠B=60°,∠C=30°。求证:△ABD是等边三角形.
证明:∵DE垂直平分AC
∴AD=CD,
∴∠DAC=∠C=30°,
∵∠ADB是△ADC的外角
∴∠ADB= ∠DAC+ ∠C=60°
∵∠B=60°
∴△ABD是等边三角形.
A
D
E
C
B
课堂小结
今天我们收获了哪些知识?
(畅所欲言)
等边三角形的性质是什么?
2.你能说一说等边三角形与等腰三角形的区别和联系吗?
3.如何判定一个三角形是等边三角形呢?
实战演练
1.如图,在等边三角形ABC中AD⊥BC,点E为AD上一点,∠CED=55°,则∠ABE等于是( )
A.10° B.15° C.20° D.25 °
D
2.如图,四边形ABCD是正方形,以CD为一边作等边△CDE,连接BE,则∠BEC为______.
15°
B
D
C
E
A
A
B
E
D
C
实战演练
3.如图,在四边形ABCD中,AB=AD,CB=CD, ∠A=60°,点E为AD 上一点,连接BD,CE交于点F,CE∥AB
(1)判断△DEF的形状,并说明理由.
(2)若AD=12,CE=8,求CF的长.
证明:(1)△DEF是等边三角形,理由如下:
∵AB=AD,
∴∠ABD=∠ADB,
∵∠A=60°,
∴∠ABD=∠ADB=60°,
A
F
E
C
D
B
实战演练
3.如图,在四边形ABCD中,AB=AD,CB=CD, ∠A=60°,点E为AD 上一点,连接BD,CE交于点F,CE∥AB
(1)判断△DEF的形状,并说明理由.
(2)若AD=12,CE=8,求CF的长.
∵ CE∥AB ,
∴∠DEF=∠A=60°,
∴∠EFD=60°,
∴△DEF是等边三角形,
A
F
E
C
D
B
实战演练
3.如图,在四边形ABCD中,AB=AD,CB=CD, ∠A=60°,点E为AD 上一点,连接BD,CE交于点F,CE∥AB
(1)判断△DEF的形状,并说明理由.
(2)若AD=12,CE=8,求CF的长.
(2)连接AC,
∵AB=AD,∠A=60°,
∴△ABD是等边三角形,
∵ AB=AD,CB=CD,
∴AC垂直平分BD,
A
F
E
C
D
B
实战演练
3.如图,在四边形ABCD中,AB=AD,CB=CD, ∠A=60°,点E为AD 上一点,连接BD,CE交于点F,CE∥AB
(1)判断△DEF的形状,并说明理由.
(2)若AD=12,CE=8,求CF的长.
∴∠DAC=30°,
∵∠DEF=60°,
∴∠ECA=∠DEF-∠EAC=30°,
∴∠ECA=∠EAC,
∴AE=CE=8,
A
F
E
C
D
B
实战演练
3.如图,在四边形ABCD中,AB=AD,CB=CD, ∠A=60°,点E为AD 上一点,连接BD,CE交于点F,CE∥AB
(1)判断△DEF的形状,并说明理由.
(2)若AD=12,CE=8,求CF的长.
∴DE=AD-AE=12-8=4,
∵△DEF是等边三角形,
∴EF=ED=4,
∴CF=CE-EF=4.
A
F
E
C
D
B
课后作业
教材83页习题13.3第12、14题.
https://www.21cnjy.com/help/help_extract.php
