第26章 章末核心心要点分类整合 复习课件(55张PPT)人教版数学九年级下册
文档属性
| 名称 | 第26章 章末核心心要点分类整合 复习课件(55张PPT)人教版数学九年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 15:10:44 | ||
图片预览











文档简介
(共55张PPT)
章末核心要点分类整合
第二十六章 反比例函数
1. 双曲线y=中k的几何意义:设P是双曲线y=上任意一点,过P向x轴、y轴作垂线,垂足分别为H,G,连接PO(O为坐标原点),则S△POH=S△POG=,S矩形PHOG=|k|.
2. 用待定系数法求反比例函数解析式的步骤:一设、二代、三解、四写.
3. 用反比例函数解实际问题的五步骤:审、设、列、写、解.
专题
反比例函数的图象
1
链接中考 >> 熟练掌握反比例函数的图象是学好反比例函数性质的重要基础,也是区别于一次函数、二次函数的关键所在. 因此,在中考中占有重要地位. 一般以选择题形式考查.
例 1
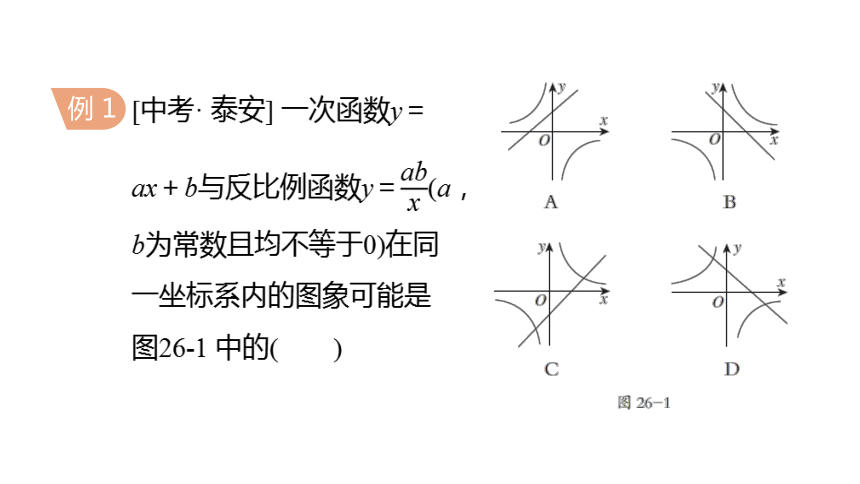
[中考· 泰安] 一次函数y=ax+b与反比例函数y=(a,b为常数且均不等于0)在同一坐标系内的图象可能是图26-1 中的( )
解题秘方:对a,b的取值分四种情况讨论,结合函数图象进行判断.
解:分四种情况:
(1)当a>0,b>0时, 一次函数y=ax+b的图象经过第一、二、三象限,此时反比例函数y=的图象分别位于第一、三象限,无选项符合;
(2)当a>0,b<0时, 一次函数y=ax+b的图象经过第一、三、四象限,此时反比例函数y=的图象分别位于第二、四象限,无选项符合;
(3)当a<0,b>0时, 一次函数y=ax+b的图象经过第一、二、四象限,此时反比例函数y=的图象分别位于第二、四象限,D选项符合;
(4)当a<0,b<0时, 一次函数y=ax+b的图象经过第二、三、四象限,此时反比例函数y=的图象分别位于第一、三象限,无选项符合.
答案:D
专题
反比例函数的性质
2
链接中考 >> 利用反比例函数的性质主要解决一些函数值的大小比较问题,中考中以选择题和填空题为主,有时也与不等式结合在一起命题.
[中考·天津] 若点A(x1,-1),B(x2,1),C(x3,5)都在反比例函数y=的图象上,则x1,x2,x3的大小关系是( )
A. x1<x2<x3 B. x1<x3<x2
C. x3<x2<x1 D. x2<x1<x3
例 2
解题秘方:紧扣反比例函数的性质求解,关键是识别几个点是否在同一个象限内.
解:∵ k=5>0,∴反比例函数y=的图象分别位于第一、三象限,在每个象限内,y随x的增大而减小.
又∵ A(x1,-1),B(x2,1),C(x3,5)都在反比例函数y=的图象上,
∴ A(x1,-1)在第三象限,B(x2,1),C(x3,5)在第一象限,且x3<x2.
∴ x1<0,x2>x3>0.
∴ x1<x3<x2.
答案:B
专题
反比例函数与一次函数的综合
3
链接中考 >> 解答反比例函数与一次函数结合在一起的综合题时,要挖掘题目中的条件,并结合图象找出图象中的关键点,求出函数解析式,并根据题中数量之间的关系,列出所需要的方程或关系式进行解答.
例 3
[中考·内江] 如图26-2,一次函数y=ax+b的图象与反比例函数y=的图象相交于A,B两点,其中点A的坐标为(-2,3),点B的坐标为(3,n).
解题秘方:紧扣一次函数与反比例函数图象的交点坐标,结合方程或不等式求解.
解:∵ 反比例函数y=的图象经过A,B两点,其中点A 的坐标为(-2,3),点B的坐标为(3,n),
∴ k=-2×3=3×n. ∴ k=-6,n=-2 .
∴ 反比例函数的解析式为y=-,B(3,-2).
(1)求这两个函数的解析式;
∵ A(-2 ,3),B(3,-2)在一次函数y=ax+b的图象上,
∴解得
∴一次函数的解析式为y=-x+1.
解:关于x的不等式ax+b<的解集为-2<x<0 或x>3.
(2)根据图象,直接写出关于x的不等式ax+b<的解集.
专题
反比例函数中比例系数k的几何意义
4
链接中考 >> 反比例函数中的比例系数k具有一定的几何意义,k的绝对值等于反比例函数图象上任意一点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积. 在反比例函数的图象中,涉及三角形或矩形的面积时,常用比例系数k的几何意义求解.
[中考·齐齐哈尔] 如图26-3,点A在反比例函数y=(k≠ 0)图象的一支上,点B在反比例函数y=-图象的一支上,点C,D在x轴上,若四边
形ABCD是面积为9 的正方形,
则实数k的值为_______.
例 4
-6
解题秘方:紧扣反比例函数解析式中k的几何意义求解,用k表示出几何图形的面积是解题的关键.
解:方法一:∵点A在双曲线y=(k≠0)上,点B在双曲线y=-上,正方形ABCD的面积为9,∴+|k|=9.
又∵ k<0,∴ k=-6.
方法二:∵ 正方形ABCD的面积为9,
∴ AD=BC=AB=3. ∴ A(,3),B(-,3).
∴ AB=--=3,解得k=-6.
专题
反比例函数的应用
5
链接中考 >> 用反比例函数刻画实际问题中两个变量之间的关系以及用反比例函数的性质解决实际问题是中考命题的重点,尤其用反比例函数的图象来反映实际问题中变量之间的关系是中考命题的热点. 解决这类问题,一是要表示出函数解析式,二是要注意自变量的取值范围.
例 5
[中考·吉林] 笑笑同学通过学习数学和物理知识,知道了电磁波的波长λ(单位:m)会随着电磁波的频率f (单位:MHz)的变化而变化. 已知波长λ与频率f是反比例函数关系,下面是它们的部分对应值:
频率f /MHz 10 15 50
波长λ/m 30 20 6
(1)求波长λ关于频率f的函数解析式;
解:设波长λ关于频率f的函数解析式为λ=(k≠0).
把(10,30)代入上式,得=30,解得k=300.
∴λ=.
(2)当f=75 MHz时,求此电磁波的波长λ .
解:当f=75 MHz时,λ==4(m).
∴ 当f=75 MHz时,此电磁波的波长λ为4 m .
专题
数形结合思想
6
专题解读>> 数形结合思想是将数(量)与形(图)结合起来进行分析、研究,从而解决问题的一种思维策略. 反比例函数的图象可以体现反比例函数的性质,所以解决有关反比例函数问题时,可以把函数图象与解析式有机地结合起来,使数学问题更直观,而且更容易解决.
[中考·苏州] 如图26-4,△ABC中,AC=BC,∠ACB=90°,A(-2,0),C(6,0),反比例函数y=(k ≠ 0,x>0)的图象与AB交于点D(m,4),与BC交于点E.
例 6
(1)求m,k的值;
解:∵ A(-2 ,0),C(6,0),∴ AC=8.
又∵ AC=BC,∴ BC=8.
又∵∠ACB=90°,∴ B(6,8).
设直线AB的函数解析式为y=ax+b,
将 A(-2,0),B(6,8)的坐标代入,
得解得
∴直线AB的函数解析式为y=x+2.
将D(m,4)的坐标代入y=x+2 ,得m=2 .
∴ D(2,4),
将D(2,4)的坐标代入y=,得4=,解得k=8.
(2)P为反比例函数y=(k ≠ 0,x>0)图象上一动点(点P在D,E之间运动,不与D,E重合),过点P作PM∥AB,交y轴于点M,过点P作PN∥x轴,交BC于点N,连接MN,求△PMN面积的最大值,并求出此时点P的坐标.
解:如图26-4,延长NP交y轴于点Q,交AB于点L.
∵AC=BC,∠ACB=90°,∴∠BAC=45°.
∵ PN∥x轴,
∴∠BLN=∠BAC=45°,∠NQM=90°.
∵ AB∥MP,∴∠MPL=∠BLP=45°.
∴∠QMP=90°-45°=45°=∠QPM.
∴ QM=QP.
设点P的坐标为(t,),则PQ=t,PN=6-t,∴MQ=t.
∴ S△PMN=PN·MQ=(6-t)·t=-(t-3)2+.
∴ 当t=3时,S△PMN有最大值,此时P(3,).
专题
方程思想
7
专题解读>> 方程思想就是从问题情境的数量关系入手,运用数学语言将题目中的条件转化为方程(或方程组),然后通过解方程(或方程组)使问题获解. 反比例函数中的方程思想主要体现在运用方程组求函数图象的交点坐标.
[中考·达州]如图26-5,一次函数y=kx+b(k,b为常数,k ≠ 0)的图象与反比例函数y=(m为常数,m≠0)的图象交于点A(2,3),B(a,-2).
例 7
(1)求反比例函数和一次函数的解析式;
解:将点A,B的坐标代入反比例函数解析式,得m=2×3=-2a,解得a=-3,m=6,∴ 反比例函数的解析式为y=,点B的坐标为(-3,-2).
将点A,B的坐标代入一次函数解析式,
得解得
∴一次函数的解析式为y=x+1 .
(2)若点C是x轴正半轴上的一点,且∠BCA=90°,求点C的坐标.
解:设点C的坐标为(x,0).
由点A,B,C的坐标得AB2=50,AC2=(x-2)2+9,BC2=(x+3)2+4. ∵∠BCA=90°,∴ AB2=AC2+BC2,
即50=(x-2)2+9+(x+3)2+4,
解得x=3或x=-4(舍去). ∴ C(3,0).
类型
巧用待定系数法求函数解析式
1
1. 已知y=y1+y2,y1与x+1成正比例,y2与x成反比例,且当x=1时,y=0;当x=4时,y=9.求:
(1)y与x的函数解析式;
(2)当x=-1时,y的值.
类型
巧用反比例函数的性质比较大小
2
2. [中考·浙江]反比例函数y=的图象上有P(t,y1),Q(t+4,y2)两点. 下列正确的选项是( )
A. 当t<-4时,y2<y1<0
B. 当-4<t<0时,y2<y1<0
C. 当-4<t<0时,0<y1<y2
D. 当t>0时,0<y1<y2
A
类型
巧用反比例函数中比例系数k的几何意义求面积
3
3. [模拟·银川]如图,A,B是反比例函数y=(x>0)图象上的两点,连接OA,OB. 过点A作AC⊥x轴于点C,交OB于点D,点B的坐标为(6,2),若D为AC的
中点,则△AOD的面积为______.
3
4. [中考·聊城]已知二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c的图象和反比例函数y=的图象在同一坐标系中大致为( )
D
类型
巧用反比例函数图象特点解两图象共存问题
4
类型
巧用反比例函数与一次函数解决问题
5
5. [中考·安徽]已知反比例函数y=(k ≠ 0)与一次函数y=2-x的图象的一个交点的横坐标为3,则k的值为( )
A.-3 B.-1
C. 1 D. 3
A
6. [中考·广安]如图,一次函数y=ax+b(a,b为常数,a ≠ 0)的图象与反比例函数y=(k为常数,k ≠ 0)的图象交于A(2,4),B(n,-2)两点.
(1)求一次函数和反比例函数的解析式;
(2)直线AB与x轴交于点C,点P(m,0)是x轴上的点,若△PAC的面积大于12,请直接写出m的取值范围.
解:m>4或m<-8.
类型
巧用反比例函数解决几何问题
6
7. [中考·福建]如图,在平面直角坐标系xOy中,反比例函数的图象与⊙O交于A,B两点,且点A,B都在第一象限. 若A(1,2),则点B的坐标为_______.
(2,1)
8. [中考·连云港]如图①,在平面直角坐标系xOy中,一次函数y=kx+1(k ≠ 0)的图象与反比例函数y=的图象交于点A,B,与y轴交于点C,点A的横坐标为2.
(1)求k的值;
(2)利用图象直接写出kx+1< 时x的取值范围;
x<-3或0<x<2.
(3)如图②,将直线AB沿y轴向下平移4个单位长度,与函数y=(x>0)的图象交于点D,与y轴交于点E,再将函数y=(x>0)的图象沿AB平移,使点A,D分
别平移到点C,F处,求图中阴影部分的
面积.
类型
巧用反比例函数解决实际问题
7
9. 王老师外出学习入住宾馆的房间后立即打开空调,将最高温度调至26 ℃,入住一段时间后关闭空调. 已知空调关闭后,室内的温度与时间近似成反比例关系,下列图象反映了王老师入住房间后一段
时间内,室内的温度y(℃)与时间
t(min)的关系,请根据图象解答
下列问题:
(1)王老师入住多长时间关闭的空调?
解:王老师入住40 min后关闭的空调.
(2)分别求室内的温度上升和下降两个阶段y与t之间的函数解析式.
(3)室内温度保持不低于20 ℃的时间是多少分钟?
章末核心要点分类整合
第二十六章 反比例函数
1. 双曲线y=中k的几何意义:设P是双曲线y=上任意一点,过P向x轴、y轴作垂线,垂足分别为H,G,连接PO(O为坐标原点),则S△POH=S△POG=,S矩形PHOG=|k|.
2. 用待定系数法求反比例函数解析式的步骤:一设、二代、三解、四写.
3. 用反比例函数解实际问题的五步骤:审、设、列、写、解.
专题
反比例函数的图象
1
链接中考 >> 熟练掌握反比例函数的图象是学好反比例函数性质的重要基础,也是区别于一次函数、二次函数的关键所在. 因此,在中考中占有重要地位. 一般以选择题形式考查.
例 1
[中考· 泰安] 一次函数y=ax+b与反比例函数y=(a,b为常数且均不等于0)在同一坐标系内的图象可能是图26-1 中的( )
解题秘方:对a,b的取值分四种情况讨论,结合函数图象进行判断.
解:分四种情况:
(1)当a>0,b>0时, 一次函数y=ax+b的图象经过第一、二、三象限,此时反比例函数y=的图象分别位于第一、三象限,无选项符合;
(2)当a>0,b<0时, 一次函数y=ax+b的图象经过第一、三、四象限,此时反比例函数y=的图象分别位于第二、四象限,无选项符合;
(3)当a<0,b>0时, 一次函数y=ax+b的图象经过第一、二、四象限,此时反比例函数y=的图象分别位于第二、四象限,D选项符合;
(4)当a<0,b<0时, 一次函数y=ax+b的图象经过第二、三、四象限,此时反比例函数y=的图象分别位于第一、三象限,无选项符合.
答案:D
专题
反比例函数的性质
2
链接中考 >> 利用反比例函数的性质主要解决一些函数值的大小比较问题,中考中以选择题和填空题为主,有时也与不等式结合在一起命题.
[中考·天津] 若点A(x1,-1),B(x2,1),C(x3,5)都在反比例函数y=的图象上,则x1,x2,x3的大小关系是( )
A. x1<x2<x3 B. x1<x3<x2
C. x3<x2<x1 D. x2<x1<x3
例 2
解题秘方:紧扣反比例函数的性质求解,关键是识别几个点是否在同一个象限内.
解:∵ k=5>0,∴反比例函数y=的图象分别位于第一、三象限,在每个象限内,y随x的增大而减小.
又∵ A(x1,-1),B(x2,1),C(x3,5)都在反比例函数y=的图象上,
∴ A(x1,-1)在第三象限,B(x2,1),C(x3,5)在第一象限,且x3<x2.
∴ x1<0,x2>x3>0.
∴ x1<x3<x2.
答案:B
专题
反比例函数与一次函数的综合
3
链接中考 >> 解答反比例函数与一次函数结合在一起的综合题时,要挖掘题目中的条件,并结合图象找出图象中的关键点,求出函数解析式,并根据题中数量之间的关系,列出所需要的方程或关系式进行解答.
例 3
[中考·内江] 如图26-2,一次函数y=ax+b的图象与反比例函数y=的图象相交于A,B两点,其中点A的坐标为(-2,3),点B的坐标为(3,n).
解题秘方:紧扣一次函数与反比例函数图象的交点坐标,结合方程或不等式求解.
解:∵ 反比例函数y=的图象经过A,B两点,其中点A 的坐标为(-2,3),点B的坐标为(3,n),
∴ k=-2×3=3×n. ∴ k=-6,n=-2 .
∴ 反比例函数的解析式为y=-,B(3,-2).
(1)求这两个函数的解析式;
∵ A(-2 ,3),B(3,-2)在一次函数y=ax+b的图象上,
∴解得
∴一次函数的解析式为y=-x+1.
解:关于x的不等式ax+b<的解集为-2<x<0 或x>3.
(2)根据图象,直接写出关于x的不等式ax+b<的解集.
专题
反比例函数中比例系数k的几何意义
4
链接中考 >> 反比例函数中的比例系数k具有一定的几何意义,k的绝对值等于反比例函数图象上任意一点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积. 在反比例函数的图象中,涉及三角形或矩形的面积时,常用比例系数k的几何意义求解.
[中考·齐齐哈尔] 如图26-3,点A在反比例函数y=(k≠ 0)图象的一支上,点B在反比例函数y=-图象的一支上,点C,D在x轴上,若四边
形ABCD是面积为9 的正方形,
则实数k的值为_______.
例 4
-6
解题秘方:紧扣反比例函数解析式中k的几何意义求解,用k表示出几何图形的面积是解题的关键.
解:方法一:∵点A在双曲线y=(k≠0)上,点B在双曲线y=-上,正方形ABCD的面积为9,∴+|k|=9.
又∵ k<0,∴ k=-6.
方法二:∵ 正方形ABCD的面积为9,
∴ AD=BC=AB=3. ∴ A(,3),B(-,3).
∴ AB=--=3,解得k=-6.
专题
反比例函数的应用
5
链接中考 >> 用反比例函数刻画实际问题中两个变量之间的关系以及用反比例函数的性质解决实际问题是中考命题的重点,尤其用反比例函数的图象来反映实际问题中变量之间的关系是中考命题的热点. 解决这类问题,一是要表示出函数解析式,二是要注意自变量的取值范围.
例 5
[中考·吉林] 笑笑同学通过学习数学和物理知识,知道了电磁波的波长λ(单位:m)会随着电磁波的频率f (单位:MHz)的变化而变化. 已知波长λ与频率f是反比例函数关系,下面是它们的部分对应值:
频率f /MHz 10 15 50
波长λ/m 30 20 6
(1)求波长λ关于频率f的函数解析式;
解:设波长λ关于频率f的函数解析式为λ=(k≠0).
把(10,30)代入上式,得=30,解得k=300.
∴λ=.
(2)当f=75 MHz时,求此电磁波的波长λ .
解:当f=75 MHz时,λ==4(m).
∴ 当f=75 MHz时,此电磁波的波长λ为4 m .
专题
数形结合思想
6
专题解读>> 数形结合思想是将数(量)与形(图)结合起来进行分析、研究,从而解决问题的一种思维策略. 反比例函数的图象可以体现反比例函数的性质,所以解决有关反比例函数问题时,可以把函数图象与解析式有机地结合起来,使数学问题更直观,而且更容易解决.
[中考·苏州] 如图26-4,△ABC中,AC=BC,∠ACB=90°,A(-2,0),C(6,0),反比例函数y=(k ≠ 0,x>0)的图象与AB交于点D(m,4),与BC交于点E.
例 6
(1)求m,k的值;
解:∵ A(-2 ,0),C(6,0),∴ AC=8.
又∵ AC=BC,∴ BC=8.
又∵∠ACB=90°,∴ B(6,8).
设直线AB的函数解析式为y=ax+b,
将 A(-2,0),B(6,8)的坐标代入,
得解得
∴直线AB的函数解析式为y=x+2.
将D(m,4)的坐标代入y=x+2 ,得m=2 .
∴ D(2,4),
将D(2,4)的坐标代入y=,得4=,解得k=8.
(2)P为反比例函数y=(k ≠ 0,x>0)图象上一动点(点P在D,E之间运动,不与D,E重合),过点P作PM∥AB,交y轴于点M,过点P作PN∥x轴,交BC于点N,连接MN,求△PMN面积的最大值,并求出此时点P的坐标.
解:如图26-4,延长NP交y轴于点Q,交AB于点L.
∵AC=BC,∠ACB=90°,∴∠BAC=45°.
∵ PN∥x轴,
∴∠BLN=∠BAC=45°,∠NQM=90°.
∵ AB∥MP,∴∠MPL=∠BLP=45°.
∴∠QMP=90°-45°=45°=∠QPM.
∴ QM=QP.
设点P的坐标为(t,),则PQ=t,PN=6-t,∴MQ=t.
∴ S△PMN=PN·MQ=(6-t)·t=-(t-3)2+.
∴ 当t=3时,S△PMN有最大值,此时P(3,).
专题
方程思想
7
专题解读>> 方程思想就是从问题情境的数量关系入手,运用数学语言将题目中的条件转化为方程(或方程组),然后通过解方程(或方程组)使问题获解. 反比例函数中的方程思想主要体现在运用方程组求函数图象的交点坐标.
[中考·达州]如图26-5,一次函数y=kx+b(k,b为常数,k ≠ 0)的图象与反比例函数y=(m为常数,m≠0)的图象交于点A(2,3),B(a,-2).
例 7
(1)求反比例函数和一次函数的解析式;
解:将点A,B的坐标代入反比例函数解析式,得m=2×3=-2a,解得a=-3,m=6,∴ 反比例函数的解析式为y=,点B的坐标为(-3,-2).
将点A,B的坐标代入一次函数解析式,
得解得
∴一次函数的解析式为y=x+1 .
(2)若点C是x轴正半轴上的一点,且∠BCA=90°,求点C的坐标.
解:设点C的坐标为(x,0).
由点A,B,C的坐标得AB2=50,AC2=(x-2)2+9,BC2=(x+3)2+4. ∵∠BCA=90°,∴ AB2=AC2+BC2,
即50=(x-2)2+9+(x+3)2+4,
解得x=3或x=-4(舍去). ∴ C(3,0).
类型
巧用待定系数法求函数解析式
1
1. 已知y=y1+y2,y1与x+1成正比例,y2与x成反比例,且当x=1时,y=0;当x=4时,y=9.求:
(1)y与x的函数解析式;
(2)当x=-1时,y的值.
类型
巧用反比例函数的性质比较大小
2
2. [中考·浙江]反比例函数y=的图象上有P(t,y1),Q(t+4,y2)两点. 下列正确的选项是( )
A. 当t<-4时,y2<y1<0
B. 当-4<t<0时,y2<y1<0
C. 当-4<t<0时,0<y1<y2
D. 当t>0时,0<y1<y2
A
类型
巧用反比例函数中比例系数k的几何意义求面积
3
3. [模拟·银川]如图,A,B是反比例函数y=(x>0)图象上的两点,连接OA,OB. 过点A作AC⊥x轴于点C,交OB于点D,点B的坐标为(6,2),若D为AC的
中点,则△AOD的面积为______.
3
4. [中考·聊城]已知二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c的图象和反比例函数y=的图象在同一坐标系中大致为( )
D
类型
巧用反比例函数图象特点解两图象共存问题
4
类型
巧用反比例函数与一次函数解决问题
5
5. [中考·安徽]已知反比例函数y=(k ≠ 0)与一次函数y=2-x的图象的一个交点的横坐标为3,则k的值为( )
A.-3 B.-1
C. 1 D. 3
A
6. [中考·广安]如图,一次函数y=ax+b(a,b为常数,a ≠ 0)的图象与反比例函数y=(k为常数,k ≠ 0)的图象交于A(2,4),B(n,-2)两点.
(1)求一次函数和反比例函数的解析式;
(2)直线AB与x轴交于点C,点P(m,0)是x轴上的点,若△PAC的面积大于12,请直接写出m的取值范围.
解:m>4或m<-8.
类型
巧用反比例函数解决几何问题
6
7. [中考·福建]如图,在平面直角坐标系xOy中,反比例函数的图象与⊙O交于A,B两点,且点A,B都在第一象限. 若A(1,2),则点B的坐标为_______.
(2,1)
8. [中考·连云港]如图①,在平面直角坐标系xOy中,一次函数y=kx+1(k ≠ 0)的图象与反比例函数y=的图象交于点A,B,与y轴交于点C,点A的横坐标为2.
(1)求k的值;
(2)利用图象直接写出kx+1< 时x的取值范围;
x<-3或0<x<2.
(3)如图②,将直线AB沿y轴向下平移4个单位长度,与函数y=(x>0)的图象交于点D,与y轴交于点E,再将函数y=(x>0)的图象沿AB平移,使点A,D分
别平移到点C,F处,求图中阴影部分的
面积.
类型
巧用反比例函数解决实际问题
7
9. 王老师外出学习入住宾馆的房间后立即打开空调,将最高温度调至26 ℃,入住一段时间后关闭空调. 已知空调关闭后,室内的温度与时间近似成反比例关系,下列图象反映了王老师入住房间后一段
时间内,室内的温度y(℃)与时间
t(min)的关系,请根据图象解答
下列问题:
(1)王老师入住多长时间关闭的空调?
解:王老师入住40 min后关闭的空调.
(2)分别求室内的温度上升和下降两个阶段y与t之间的函数解析式.
(3)室内温度保持不低于20 ℃的时间是多少分钟?
