人教版数学八年级上册期中训练卷01(含答案)
文档属性
| 名称 | 人教版数学八年级上册期中训练卷01(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 291.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-21 17:59:13 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版数学(2024)八年级上册期中训练卷01
一、单选题
1.下列四个图形中,是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
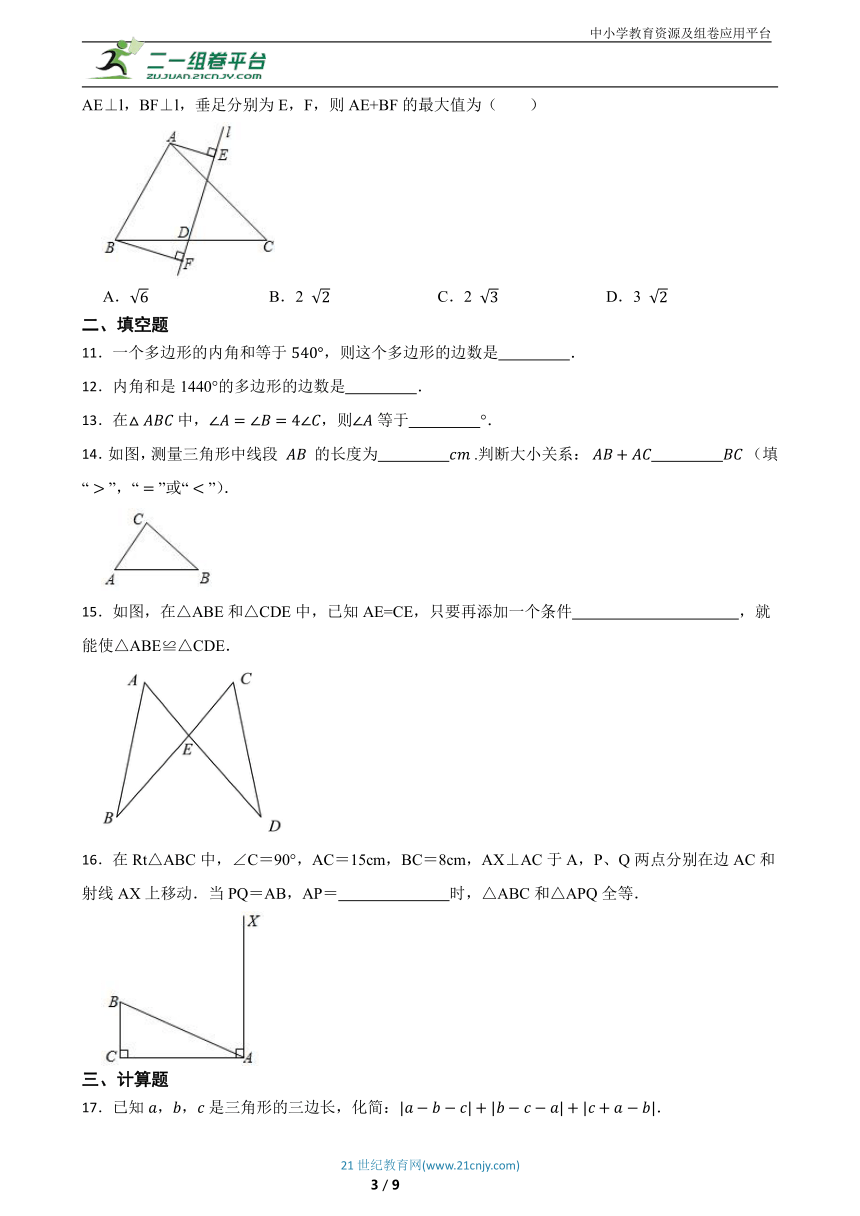
2.我国传统工艺中,油纸伞制作非常巧妙,其中蕴含着数学知识.如图是油纸伞的张开示意图,,则的依据是( )
A.SAS B.ASA C.AAS D.SSS
3.如图,在中,点、分别在、上,则图中三角形的个数是( )
A.5 B.6 C.7 D.8
4.有下列长度的三条线段,其中能组成三角形的是( )
A.,, B.,,
C.,, D.,,
5.下列图形中,不是轴对称图形的是( )
A. B. C. D.
6.如图,在中,和的平分线,相交于点,交于,交于,过点作于,下列三个结论:①;②当时,;③若,,则,其中正确的个数是( )
A.0个 B.1个 C.2个 D.3个
7.王老汉要将一块如图所示的三角形土地平均分配给两个儿子,则图中他所作的线段 AD 应该是 ABC 的( )
A.角平分线 B.中线 C.高 D.任意一条线
8.用三角尺可按下面方法画角平分线:在已知的∠AOB的两边上,分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP,则OP平分∠AOB.做法中用到证明△OMP与△ONP全等的判定方法是( )
A.SAS B.SSS C.ASA D.HL
9.如图,已知 ≌ , 是 的平分线,已知 , ,则 的度数是( ).
A. B. C. D.
10.如图,在△ABC中,AB=2,∠ABC=60°,∠ACB=45°,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为( )
A. B.2 C.2 D.3
二、填空题
11.一个多边形的内角和等于,则这个多边形的边数是 .
12.内角和是1440°的多边形的边数是 .
13.在中,,则等于 °.
14.如图,测量三角形中线段 的长度为 .判断大小关系: (填“ ”,“ ”或“ ”).
15.如图,在△ABE和△CDE中,已知AE=CE,只要再添加一个条件 ,就能使△ABE≌△CDE.
16.在Rt△ABC中,∠C=90°,AC=15cm,BC=8cm,AX⊥AC于A,P、Q两点分别在边AC和射线AX上移动.当PQ=AB,AP= 时,△ABC和△APQ全等.
三、计算题
17.已知,,是三角形的三边长,化简:.
18.解决多边形问题:
(1)一个多边形的内角和是外角和的3倍,它是几边形?
(2)小华在求一个多边形的内角和时,重复加了一个角的度数,计算结果是,这个多边形是几边形?
19.在平面直角坐标系xOy中描出下列两组点,分别将每组里的点用线段依次连接起来.
第一组:A(﹣3,3)、C(4,3);
第二组:D(﹣2,﹣1)、E(2,﹣1).
(1)直接写出线段AC与线段DE的位置关系;
(2)在(1)的条件下,线段AC,DE分别与y轴交于点B,F.若点M为射线OB上一动点(不与点O,B重合).
①当点M在线段OB上运动时,连接AM、DM,补全图形,用等式表示∠CAM、∠AMD、∠MDE之间的数量关系,并证明.
②当△ACM与△DEM面积相等时,求点M的坐标.
四、解答题
20.如图, 中,∠A=30°,∠B=70°,CE平分∠ACB交AB于点E,CD是AB边上的高,求:∠DCE的度数
21.已知O为直线AB上一点,将一直角三角板OMN的直角顶点放在点O处.射线OC平分∠MOB.
(1)如图1,若∠AOM=30°,求∠CON的度数;
(2)在图1中,若∠AOM=,直接写出∠CON的度数(用含的代数式表示);
(3)将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置,当∠AOC=3∠BON时,求∠AOM的度数.
22.利用网格线画图:如图,点A、B、C都在正方形网格的格点上.
①在BC上找一点P,使PA=PB;
②在BC上找一点Q,使点Q到AB和AC的距离相等.
23.已知,射线OP从OB出发,绕O逆时针以1°/秒的速度旋转,射线OQ从OA出发,绕O顺时针以3°/秒的速度旋转,两射线同时出发,运动时间为t秒
(1)当秒时,求;
(2)当,求的值;
(3)射线OP,OQ,OB,其中一条射线是其他两条射线所形成的角的平分线,求t的值.
答案解析部分
1.【答案】C
【知识点】轴对称图形
2.【答案】A
【知识点】三角形全等的判定-SAS
3.【答案】D
【知识点】三角形相关概念
4.【答案】B
【知识点】三角形三边关系
5.【答案】B
【知识点】轴对称图形
6.【答案】C
【知识点】三角形内角和定理;三角形的外角性质;三角形全等及其性质
7.【答案】B
【知识点】三角形的角平分线、中线和高
8.【答案】D
【知识点】直角三角形全等的判定-HL
9.【答案】A
【知识点】三角形全等及其性质
10.【答案】A
【知识点】垂线段最短及其应用;三角形全等及其性质;三角形全等的判定-AAS
11.【答案】5
【知识点】多边形内角与外角
12.【答案】10
【知识点】多边形内角与外角
13.【答案】80
【知识点】三角形内角和定理
14.【答案】;
【知识点】三角形三边关系
15.【答案】∠A=∠C或∠B=∠D
【知识点】三角形全等的判定
16.【答案】8cm或15cm
【知识点】直角三角形全等的判定-HL
17.【答案】
【知识点】整式的加减运算;三角形三边关系;化简含绝对值有理数
18.【答案】(1)八边形
(2)八边形
【知识点】一元一次不等式组的应用;多边形内角与外角
19.【答案】(1)解:∵A(﹣3,3)、C(4,3),
∴AC∥x轴,
∵D(﹣2,﹣1)、E(2,﹣1),
∴DE∥x轴,
∴AC∥DE;
(2)①如图,∠CAM+∠MDE=∠AMD.
理由如下:
过点M作MN∥AC,
∵MN∥AC(作图),
∴∠CAM=∠AMN(两直线平行,内错角相等),
∵AC∥DE(已知),
∴MN∥DE(平行公理推论),
∴∠MDE=∠NMD(两直线平行,内错角相等),
∴∠CAM+∠MDE=∠AMN+∠NMD=∠AMD(等量代换).
②由题意,得:AC=7,DE=4,
设M(0,m),
(i)当点M在线段OB上时,BM=3﹣m,FM=m+1,
∴S△ACM= AC BM= ×7×(3﹣m)= ,
S△DEM= DE FM= ×4×(m+1)=2m+2,
∵S△ACM=S△DEM,
∴ =2m+2,
解得:m= ,
∴M(0, );
(ii)当点M在线段OB的延长线上时,BM=m﹣3,FM=m+1,
∴S△ACM= AC BM= ×7×(m﹣3)= ,
S△DEM= DE FM= ×4×(m+1)=2m+2,
∵S△ACM=S△DEM,
∴ =2m+2,
解得:m= ,
∴M(0, );
综上所述,点M的坐标为(0, )或(0, ).
【知识点】角的运算;平行线的判定与性质;三角形的面积
20.【答案】解:∵∠A=30°,∠B=70°
∴∠ACB=180°-∠A-∠B=80°
∵CE平分∠ACB
∴∠BCE=
∵CD是AB边上的高
∴∠BDC=90°
∴∠BCD=90°-∠B =20°
∴∠DCE=∠BCE—∠BCD=40°-20°=20°.
【知识点】三角形的角平分线、中线和高;三角形内角和定理
21.【答案】(1)15°;(2);(3)144°
【知识点】角的运算;余角、补角及其性质;角平分线的性质;一元一次方程的实际应用-几何问题
22.【答案】解:①如图所示:点P即为所求;
②如图所示:点Q即为所求.
【知识点】角平分线的性质;线段垂直平分线的性质
23.【答案】(1);(2)当或60时,;(3)当或时,、、其中一条射线是其他两条射线所形成的角的平分线
【知识点】角的运算;角平分线的性质
21世纪教育网(www.21cnjy.com)
1 / 1
人教版数学(2024)八年级上册期中训练卷01
一、单选题
1.下列四个图形中,是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
2.我国传统工艺中,油纸伞制作非常巧妙,其中蕴含着数学知识.如图是油纸伞的张开示意图,,则的依据是( )
A.SAS B.ASA C.AAS D.SSS
3.如图,在中,点、分别在、上,则图中三角形的个数是( )
A.5 B.6 C.7 D.8
4.有下列长度的三条线段,其中能组成三角形的是( )
A.,, B.,,
C.,, D.,,
5.下列图形中,不是轴对称图形的是( )
A. B. C. D.
6.如图,在中,和的平分线,相交于点,交于,交于,过点作于,下列三个结论:①;②当时,;③若,,则,其中正确的个数是( )
A.0个 B.1个 C.2个 D.3个
7.王老汉要将一块如图所示的三角形土地平均分配给两个儿子,则图中他所作的线段 AD 应该是 ABC 的( )
A.角平分线 B.中线 C.高 D.任意一条线
8.用三角尺可按下面方法画角平分线:在已知的∠AOB的两边上,分别取OM=ON,再分别过点M,N作OA,OB的垂线,交点为P,画射线OP,则OP平分∠AOB.做法中用到证明△OMP与△ONP全等的判定方法是( )
A.SAS B.SSS C.ASA D.HL
9.如图,已知 ≌ , 是 的平分线,已知 , ,则 的度数是( ).
A. B. C. D.
10.如图,在△ABC中,AB=2,∠ABC=60°,∠ACB=45°,D是BC的中点,直线l经过点D,AE⊥l,BF⊥l,垂足分别为E,F,则AE+BF的最大值为( )
A. B.2 C.2 D.3
二、填空题
11.一个多边形的内角和等于,则这个多边形的边数是 .
12.内角和是1440°的多边形的边数是 .
13.在中,,则等于 °.
14.如图,测量三角形中线段 的长度为 .判断大小关系: (填“ ”,“ ”或“ ”).
15.如图,在△ABE和△CDE中,已知AE=CE,只要再添加一个条件 ,就能使△ABE≌△CDE.
16.在Rt△ABC中,∠C=90°,AC=15cm,BC=8cm,AX⊥AC于A,P、Q两点分别在边AC和射线AX上移动.当PQ=AB,AP= 时,△ABC和△APQ全等.
三、计算题
17.已知,,是三角形的三边长,化简:.
18.解决多边形问题:
(1)一个多边形的内角和是外角和的3倍,它是几边形?
(2)小华在求一个多边形的内角和时,重复加了一个角的度数,计算结果是,这个多边形是几边形?
19.在平面直角坐标系xOy中描出下列两组点,分别将每组里的点用线段依次连接起来.
第一组:A(﹣3,3)、C(4,3);
第二组:D(﹣2,﹣1)、E(2,﹣1).
(1)直接写出线段AC与线段DE的位置关系;
(2)在(1)的条件下,线段AC,DE分别与y轴交于点B,F.若点M为射线OB上一动点(不与点O,B重合).
①当点M在线段OB上运动时,连接AM、DM,补全图形,用等式表示∠CAM、∠AMD、∠MDE之间的数量关系,并证明.
②当△ACM与△DEM面积相等时,求点M的坐标.
四、解答题
20.如图, 中,∠A=30°,∠B=70°,CE平分∠ACB交AB于点E,CD是AB边上的高,求:∠DCE的度数
21.已知O为直线AB上一点,将一直角三角板OMN的直角顶点放在点O处.射线OC平分∠MOB.
(1)如图1,若∠AOM=30°,求∠CON的度数;
(2)在图1中,若∠AOM=,直接写出∠CON的度数(用含的代数式表示);
(3)将图1中的直角三角板OMN绕顶点O顺时针旋转至图2的位置,当∠AOC=3∠BON时,求∠AOM的度数.
22.利用网格线画图:如图,点A、B、C都在正方形网格的格点上.
①在BC上找一点P,使PA=PB;
②在BC上找一点Q,使点Q到AB和AC的距离相等.
23.已知,射线OP从OB出发,绕O逆时针以1°/秒的速度旋转,射线OQ从OA出发,绕O顺时针以3°/秒的速度旋转,两射线同时出发,运动时间为t秒
(1)当秒时,求;
(2)当,求的值;
(3)射线OP,OQ,OB,其中一条射线是其他两条射线所形成的角的平分线,求t的值.
答案解析部分
1.【答案】C
【知识点】轴对称图形
2.【答案】A
【知识点】三角形全等的判定-SAS
3.【答案】D
【知识点】三角形相关概念
4.【答案】B
【知识点】三角形三边关系
5.【答案】B
【知识点】轴对称图形
6.【答案】C
【知识点】三角形内角和定理;三角形的外角性质;三角形全等及其性质
7.【答案】B
【知识点】三角形的角平分线、中线和高
8.【答案】D
【知识点】直角三角形全等的判定-HL
9.【答案】A
【知识点】三角形全等及其性质
10.【答案】A
【知识点】垂线段最短及其应用;三角形全等及其性质;三角形全等的判定-AAS
11.【答案】5
【知识点】多边形内角与外角
12.【答案】10
【知识点】多边形内角与外角
13.【答案】80
【知识点】三角形内角和定理
14.【答案】;
【知识点】三角形三边关系
15.【答案】∠A=∠C或∠B=∠D
【知识点】三角形全等的判定
16.【答案】8cm或15cm
【知识点】直角三角形全等的判定-HL
17.【答案】
【知识点】整式的加减运算;三角形三边关系;化简含绝对值有理数
18.【答案】(1)八边形
(2)八边形
【知识点】一元一次不等式组的应用;多边形内角与外角
19.【答案】(1)解:∵A(﹣3,3)、C(4,3),
∴AC∥x轴,
∵D(﹣2,﹣1)、E(2,﹣1),
∴DE∥x轴,
∴AC∥DE;
(2)①如图,∠CAM+∠MDE=∠AMD.
理由如下:
过点M作MN∥AC,
∵MN∥AC(作图),
∴∠CAM=∠AMN(两直线平行,内错角相等),
∵AC∥DE(已知),
∴MN∥DE(平行公理推论),
∴∠MDE=∠NMD(两直线平行,内错角相等),
∴∠CAM+∠MDE=∠AMN+∠NMD=∠AMD(等量代换).
②由题意,得:AC=7,DE=4,
设M(0,m),
(i)当点M在线段OB上时,BM=3﹣m,FM=m+1,
∴S△ACM= AC BM= ×7×(3﹣m)= ,
S△DEM= DE FM= ×4×(m+1)=2m+2,
∵S△ACM=S△DEM,
∴ =2m+2,
解得:m= ,
∴M(0, );
(ii)当点M在线段OB的延长线上时,BM=m﹣3,FM=m+1,
∴S△ACM= AC BM= ×7×(m﹣3)= ,
S△DEM= DE FM= ×4×(m+1)=2m+2,
∵S△ACM=S△DEM,
∴ =2m+2,
解得:m= ,
∴M(0, );
综上所述,点M的坐标为(0, )或(0, ).
【知识点】角的运算;平行线的判定与性质;三角形的面积
20.【答案】解:∵∠A=30°,∠B=70°
∴∠ACB=180°-∠A-∠B=80°
∵CE平分∠ACB
∴∠BCE=
∵CD是AB边上的高
∴∠BDC=90°
∴∠BCD=90°-∠B =20°
∴∠DCE=∠BCE—∠BCD=40°-20°=20°.
【知识点】三角形的角平分线、中线和高;三角形内角和定理
21.【答案】(1)15°;(2);(3)144°
【知识点】角的运算;余角、补角及其性质;角平分线的性质;一元一次方程的实际应用-几何问题
22.【答案】解:①如图所示:点P即为所求;
②如图所示:点Q即为所求.
【知识点】角平分线的性质;线段垂直平分线的性质
23.【答案】(1);(2)当或60时,;(3)当或时,、、其中一条射线是其他两条射线所形成的角的平分线
【知识点】角的运算;角平分线的性质
21世纪教育网(www.21cnjy.com)
1 / 1
同课章节目录
