2025北师大版高中数学必修第二册强化练习题--1.1 构成空间几何体的基本元素 1.2 简单多面体——棱柱、棱锥和棱台
文档属性
| 名称 | 2025北师大版高中数学必修第二册强化练习题--1.1 构成空间几何体的基本元素 1.2 简单多面体——棱柱、棱锥和棱台 |

|
|
| 格式 | docx | ||
| 文件大小 | 441.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025北师大版高中数学必修第二册
第六章 立体几何初步
§1 基本立体图形
1.1 构成空间几何体的基本元素
1.2 简单多面体——棱柱、棱锥和棱台
基础过关练
题组一 空间几何体的基本元素
1.下列不属于构成空间几何体的基本元素的是 ( )
A.点
B.线
C.曲面
D.多边形(不包括内部的点)
2.在第24届冬奥会上,中国代表队创造了历史最好成绩,首都北京也成为第一座“双奥之城”.如图所示,坐落于北京的国家游泳中心(又称“水立方”)是中国健儿为国争光的地方,“水立方”可以抽象出的几何体是( )
A.圆柱 B.四棱锥
C.四棱台 D.长方体
题组二 棱柱的结构特征
3.(2024广东惠州六校联考)下列说法不正确的是( )
A.直四棱柱是长方体
B.正方体是平行六面体
C.长方体是平行六面体
D.平行六面体是四棱柱
4.(2023四川眉山月考)某同学制作了一个对面图案均相同的正方体礼品盒,如图所示,则这个正方体礼品盒的表面展开图应该为( )
5.如图,长方体ABCD-A1B1C1D1.
(1)这个长方体是棱柱吗 如果是,是几棱柱 为什么
(2)用平面BCNM把这个长方体分成两部分,各部分形成的几何体还是棱柱吗 如果是,请说明是几棱柱,并用符号表示;如果不是,请说明理由.
题组三 棱锥的结构特征
6.下列说法中,正确的是( )
①棱锥的各个侧面都是三角形;②有一个面是多边形,其余各面都是三角形,由这些面围成的几何体是棱锥;③四面体的任何一个面都可以作为棱锥的底面;④棱锥的各侧棱长相等.
A.①② B.①③ C.②③ D.②④
7.(2024河北邢台期中)在四面体D-ABC中,已知底面ABC为正三角形,则“三棱锥D-ABC为正三棱锥”是“△ABD与△BCD均为等腰三角形”的( )
A.充要条件
B.必要不充分条件
C.充分不必要条件
D.既不充分也不必要条件
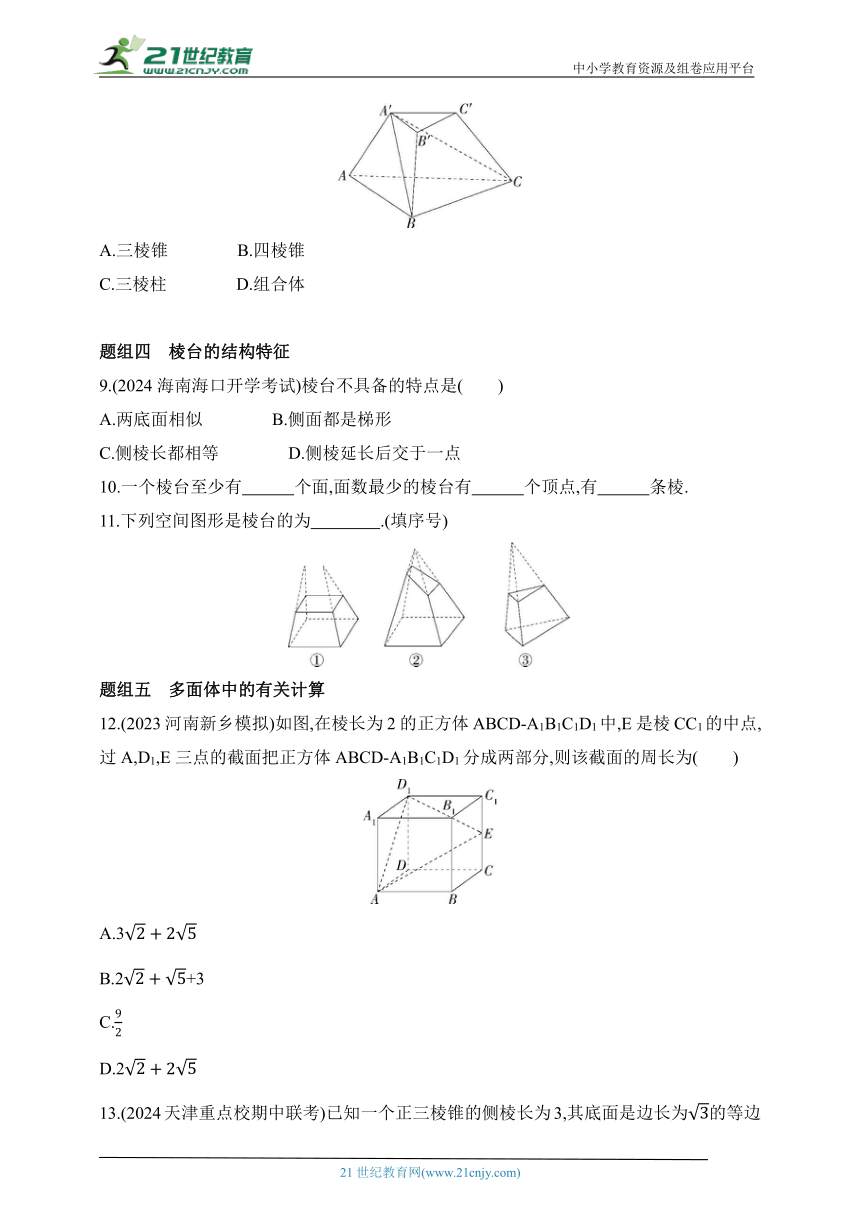
8.(2023安徽淮北一模)如图所示,在三棱台ABC-A'B'C'中,沿面A'BC截去三棱锥A'-ABC,则剩余的部分是( )
A.三棱锥 B.四棱锥
C.三棱柱 D.组合体
题组四 棱台的结构特征
9.(2024海南海口开学考试)棱台不具备的特点是( )
A.两底面相似 B.侧面都是梯形
C.侧棱长都相等 D.侧棱延长后交于一点
10.一个棱台至少有 个面,面数最少的棱台有 个顶点,有 条棱.
11.下列空间图形是棱台的为 .(填序号)
题组五 多面体中的有关计算
12.(2023河南新乡模拟)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,过A,D1,E三点的截面把正方体ABCD-A1B1C1D1分成两部分,则该截面的周长为( )
A.3
B.2+3
C.
D.2
13.(2024天津重点校期中联考)已知一个正三棱锥的侧棱长为3,其底面是边长为的等边三角形,则此正三棱锥的高为 .
14.(2024山西临汾期中)一个正四棱台的下底面周长与上底面周长之差为16,且侧面梯形的高为2,则该正四棱台的高为 .
15.(2024辽宁抚顺德才高级中学月考)如图,已知四棱锥V-ABCD的底面是面积为16的正方形,侧面是全等的等腰三角形,侧棱长为6.
(1)求四棱锥V-ABCD的高;
(2)求四棱锥V-ABCD的斜高.
答案与分层梯度式解析
第六章 立体几何初步
§1 基本立体图形
1.1 构成空间几何体的基本元素
1.2 简单多面体——棱柱、棱锥和棱台
基础过关练
1.D
2.D
3.A 直四棱柱的侧棱垂直于底面,当底面不是矩形时直四棱柱不是长方体,故A错误;
平行六面体的对面平行,底面为平行四边形,故B、C、D均正确,故选A.
4.A 无论沿正方体的哪条棱剪开,相邻面在展开图中可以不相邻,未剪开的相邻面在展开图中一定相邻,又正方体对面的图案相同,所以展开后相同图案绝不会相邻.故选A.
5.解析 (1)是棱柱,是四棱柱,因为长方体有相对的两个面是互相平行的四边形(作底面),其余各面都是矩形(作侧面),且相邻侧面的公共边互相平行,符合棱柱的定义,又底面是四边形,所以长方体是四棱柱.
(2)是.截面BCNM的右上方部分是三棱柱BB1M-CC1N,左下方部分是四棱柱ABMA1-DCND1.
6.B 由棱锥的定义知①正确;②中没有强调三角形有一个公共顶点,故②错误;四面体是由四个三角形面所围成的封闭几何体,因此以四面体的任何一个面作底面的几何体都是三棱锥,故③正确;棱锥的侧棱长可以相等,也可以不相等,故④错误.故选B.
7.C 正三棱锥的底面为正三角形,侧面为全等的等腰三角形,故充分性成立;
当△ABD与△BCD均为等腰三角形,但不全等时,如AB=BC=AC=CD=2,AD=BD=3,此时三棱锥不是正三棱锥,必要性不成立,故为充分不必要条件.故选C.
8.B 截去三棱锥后剩余部分是四棱锥A'-BCC'B'.故选B.
9.C 因为棱锥的侧棱不一定相等,所以截得的棱台的侧棱也不一定相等.
10.答案 5;6;9
解析 面数最少的棱台为三棱台,它有5个面,6个顶点,9条棱.
11.答案 ③
解析 由棱台的定义知,棱台的上、下底面平行,且侧棱的延长线能交于一点.
①中,侧棱延长后不能交于一点;②中,上、下底面不平行;③符合棱台的结构特征.
12.A 取BC的中点F,连接AF,EF,则四边形AFED1为截面四边形,
因为正方体ABCD-A1B1C1D1的棱长为2,
所以EF=,
所以四边形AFED1的周长为3.
13.答案 2
解析 如图,
在正三棱锥P-ABC中,PA=3,AB=,
由正三棱锥的性质可知,顶点P在底面内的射影为正三角形ABC的中心,记为O,
取BC的中点D,连接AD,
则AO=AB·sin 60°==1,
所以PO=.
14.答案 2
解析 如图,在正四棱台ABCD-EFGH中,EQ⊥AB于点Q,EN⊥AC于点N,O,M分别为上、下底面的中心,
设棱台的上、下底面的边长分别为a,b,则4b-4a=16,即b-a=4,由题知EQ=2,则EA==4,
所以OM=EN=,
故棱台的高为2.
15.解析 (1)由于四棱锥V-ABCD的侧面是全等的等腰三角形,底面为正方形,故该四棱锥是正四棱锥,
如图,连接AC,BD,交于点O,连接VO,
则VO为正四棱锥的高,△VCO为直角三角形,且VO⊥AC,易知正方形ABCD的边长为4,则AC=4,所以OC=2,所以VO==8,
故四棱锥V-ABCD的高为8.
(2)由于正四棱锥的侧面是等腰三角形,
故四棱锥V-ABCD的斜高为.
方法技巧 在正棱锥的计算问题中要善于应用由高、斜高、斜高在底面上的射影构成的直角三角形和由高、侧棱、侧棱在底面上的射影构成的直角三角形解题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025北师大版高中数学必修第二册
第六章 立体几何初步
§1 基本立体图形
1.1 构成空间几何体的基本元素
1.2 简单多面体——棱柱、棱锥和棱台
基础过关练
题组一 空间几何体的基本元素
1.下列不属于构成空间几何体的基本元素的是 ( )
A.点
B.线
C.曲面
D.多边形(不包括内部的点)
2.在第24届冬奥会上,中国代表队创造了历史最好成绩,首都北京也成为第一座“双奥之城”.如图所示,坐落于北京的国家游泳中心(又称“水立方”)是中国健儿为国争光的地方,“水立方”可以抽象出的几何体是( )
A.圆柱 B.四棱锥
C.四棱台 D.长方体
题组二 棱柱的结构特征
3.(2024广东惠州六校联考)下列说法不正确的是( )
A.直四棱柱是长方体
B.正方体是平行六面体
C.长方体是平行六面体
D.平行六面体是四棱柱
4.(2023四川眉山月考)某同学制作了一个对面图案均相同的正方体礼品盒,如图所示,则这个正方体礼品盒的表面展开图应该为( )
5.如图,长方体ABCD-A1B1C1D1.
(1)这个长方体是棱柱吗 如果是,是几棱柱 为什么
(2)用平面BCNM把这个长方体分成两部分,各部分形成的几何体还是棱柱吗 如果是,请说明是几棱柱,并用符号表示;如果不是,请说明理由.
题组三 棱锥的结构特征
6.下列说法中,正确的是( )
①棱锥的各个侧面都是三角形;②有一个面是多边形,其余各面都是三角形,由这些面围成的几何体是棱锥;③四面体的任何一个面都可以作为棱锥的底面;④棱锥的各侧棱长相等.
A.①② B.①③ C.②③ D.②④
7.(2024河北邢台期中)在四面体D-ABC中,已知底面ABC为正三角形,则“三棱锥D-ABC为正三棱锥”是“△ABD与△BCD均为等腰三角形”的( )
A.充要条件
B.必要不充分条件
C.充分不必要条件
D.既不充分也不必要条件
8.(2023安徽淮北一模)如图所示,在三棱台ABC-A'B'C'中,沿面A'BC截去三棱锥A'-ABC,则剩余的部分是( )
A.三棱锥 B.四棱锥
C.三棱柱 D.组合体
题组四 棱台的结构特征
9.(2024海南海口开学考试)棱台不具备的特点是( )
A.两底面相似 B.侧面都是梯形
C.侧棱长都相等 D.侧棱延长后交于一点
10.一个棱台至少有 个面,面数最少的棱台有 个顶点,有 条棱.
11.下列空间图形是棱台的为 .(填序号)
题组五 多面体中的有关计算
12.(2023河南新乡模拟)如图,在棱长为2的正方体ABCD-A1B1C1D1中,E是棱CC1的中点,过A,D1,E三点的截面把正方体ABCD-A1B1C1D1分成两部分,则该截面的周长为( )
A.3
B.2+3
C.
D.2
13.(2024天津重点校期中联考)已知一个正三棱锥的侧棱长为3,其底面是边长为的等边三角形,则此正三棱锥的高为 .
14.(2024山西临汾期中)一个正四棱台的下底面周长与上底面周长之差为16,且侧面梯形的高为2,则该正四棱台的高为 .
15.(2024辽宁抚顺德才高级中学月考)如图,已知四棱锥V-ABCD的底面是面积为16的正方形,侧面是全等的等腰三角形,侧棱长为6.
(1)求四棱锥V-ABCD的高;
(2)求四棱锥V-ABCD的斜高.
答案与分层梯度式解析
第六章 立体几何初步
§1 基本立体图形
1.1 构成空间几何体的基本元素
1.2 简单多面体——棱柱、棱锥和棱台
基础过关练
1.D
2.D
3.A 直四棱柱的侧棱垂直于底面,当底面不是矩形时直四棱柱不是长方体,故A错误;
平行六面体的对面平行,底面为平行四边形,故B、C、D均正确,故选A.
4.A 无论沿正方体的哪条棱剪开,相邻面在展开图中可以不相邻,未剪开的相邻面在展开图中一定相邻,又正方体对面的图案相同,所以展开后相同图案绝不会相邻.故选A.
5.解析 (1)是棱柱,是四棱柱,因为长方体有相对的两个面是互相平行的四边形(作底面),其余各面都是矩形(作侧面),且相邻侧面的公共边互相平行,符合棱柱的定义,又底面是四边形,所以长方体是四棱柱.
(2)是.截面BCNM的右上方部分是三棱柱BB1M-CC1N,左下方部分是四棱柱ABMA1-DCND1.
6.B 由棱锥的定义知①正确;②中没有强调三角形有一个公共顶点,故②错误;四面体是由四个三角形面所围成的封闭几何体,因此以四面体的任何一个面作底面的几何体都是三棱锥,故③正确;棱锥的侧棱长可以相等,也可以不相等,故④错误.故选B.
7.C 正三棱锥的底面为正三角形,侧面为全等的等腰三角形,故充分性成立;
当△ABD与△BCD均为等腰三角形,但不全等时,如AB=BC=AC=CD=2,AD=BD=3,此时三棱锥不是正三棱锥,必要性不成立,故为充分不必要条件.故选C.
8.B 截去三棱锥后剩余部分是四棱锥A'-BCC'B'.故选B.
9.C 因为棱锥的侧棱不一定相等,所以截得的棱台的侧棱也不一定相等.
10.答案 5;6;9
解析 面数最少的棱台为三棱台,它有5个面,6个顶点,9条棱.
11.答案 ③
解析 由棱台的定义知,棱台的上、下底面平行,且侧棱的延长线能交于一点.
①中,侧棱延长后不能交于一点;②中,上、下底面不平行;③符合棱台的结构特征.
12.A 取BC的中点F,连接AF,EF,则四边形AFED1为截面四边形,
因为正方体ABCD-A1B1C1D1的棱长为2,
所以EF=,
所以四边形AFED1的周长为3.
13.答案 2
解析 如图,
在正三棱锥P-ABC中,PA=3,AB=,
由正三棱锥的性质可知,顶点P在底面内的射影为正三角形ABC的中心,记为O,
取BC的中点D,连接AD,
则AO=AB·sin 60°==1,
所以PO=.
14.答案 2
解析 如图,在正四棱台ABCD-EFGH中,EQ⊥AB于点Q,EN⊥AC于点N,O,M分别为上、下底面的中心,
设棱台的上、下底面的边长分别为a,b,则4b-4a=16,即b-a=4,由题知EQ=2,则EA==4,
所以OM=EN=,
故棱台的高为2.
15.解析 (1)由于四棱锥V-ABCD的侧面是全等的等腰三角形,底面为正方形,故该四棱锥是正四棱锥,
如图,连接AC,BD,交于点O,连接VO,
则VO为正四棱锥的高,△VCO为直角三角形,且VO⊥AC,易知正方形ABCD的边长为4,则AC=4,所以OC=2,所以VO==8,
故四棱锥V-ABCD的高为8.
(2)由于正四棱锥的侧面是等腰三角形,
故四棱锥V-ABCD的斜高为.
方法技巧 在正棱锥的计算问题中要善于应用由高、斜高、斜高在底面上的射影构成的直角三角形和由高、侧棱、侧棱在底面上的射影构成的直角三角形解题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
