2025北师大版高中数学必修第二册强化练习题--6.2 柱、锥、台的体积
文档属性
| 名称 | 2025北师大版高中数学必修第二册强化练习题--6.2 柱、锥、台的体积 |  | |
| 格式 | docx | ||
| 文件大小 | 644.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 09:26:37 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025北师大版高中数学必修第二册
6.2 柱、锥、台的体积
基础过关练
题组一 柱、锥、台的体积
1.(2022江苏南通阶段练习)一个圆锥的侧面展开图恰好是一个半径为1的半圆,则该圆锥的体积为( )
A.π
2.(2024浙江三锋教研联盟期中)如图,四面体P-ABC的各个面都是边长为2的正三角形,其中顶点A,B,C在一个圆柱的下底面圆周上,顶点P是上底面圆的圆心,则圆柱的体积是( )
A.π
3.(2023广东广州天河中学期中)正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为( )
A.20+12
4.(多选题)(2024广东惠州模拟)某班级到一工厂劳动实践,加工出如图所示的圆台O1O2,在轴截面ABCD中,AB=AD=BC=2 cm,且CD=2AB,则( )
A.该圆台的高为1 cm
B.该圆台的轴截面面积为3 cm2
C.该圆台的侧面积为6π cm2
D.该圆台的体积为 cm3
5.(2024江西南昌第十九中学等校期末调研测试)如图,已知三棱台ABC-A1B1C1的体积为V,记上、下底面面积分别为S1,S2,若S1∶S2=1∶4,则三棱锥B-A1B1C1的体积为 V.
6.(2024江西赣州期末)如图,在四棱锥P-ABCD中,四边形ABCD是边长为4的正方形,PD⊥平面ABCD,PC与平面ABCD的夹角为,E为PA上的点.
(1)若E为PA的中点,证明:PC∥平面BDE;
(2)若E为PA上靠近A的三等分点,求三棱锥C-BDE的体积.
7.(2024安徽合肥一中期中)如图所示,底面边长为4的正四棱锥P-ABCD被平行于底面的平面所截,截去一个底面边长为2,高为4的正四棱锥P-A1B1C1D1.
(1)求棱台A1B1C1D1-ABCD的体积;
(2)求棱台A1B1C1D1-ABCD的表面积.
题组二 组合体的体积
8.(2023天津河东一模)有一个由圆锥和圆柱组成的玻璃容器,其中间连通(玻璃壁厚度忽略不计),容器中装有一定体积的水,圆柱高为10,底面半径为3,圆锥高为h,底面半径大于圆柱,图1中,圆柱在下面,液面保持水平,高度为h,将容器倒置如图2所示,若水恰好充满圆锥,则圆锥的底面半径为 .
9.(2022山西运城联考)为了给热爱朗读的师生提供一个安静、独立的环境,某学校修建了若干“朗读亭”.如图所示,该朗读亭的外形是一个正六棱柱和正六棱锥的组合体,过正六棱柱两条相对侧棱的截面为正方形,若正六棱锥的侧棱长为,正六棱柱的高为2,则此组合体的体积为 .
10.如图,一个底面半径为2的圆柱被一平面所截,截得的几何体的最短和最长母线长分别为2和3,则该几何体的体积为 .
11.(2023吉林长春二中期中)如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,其高为6 cm,底面三角形的边长分别为3 cm,4 cm,5 cm,以上、下底面的内切圆为底面,挖去一个圆柱,则剩余部分的几何体的体积为 .
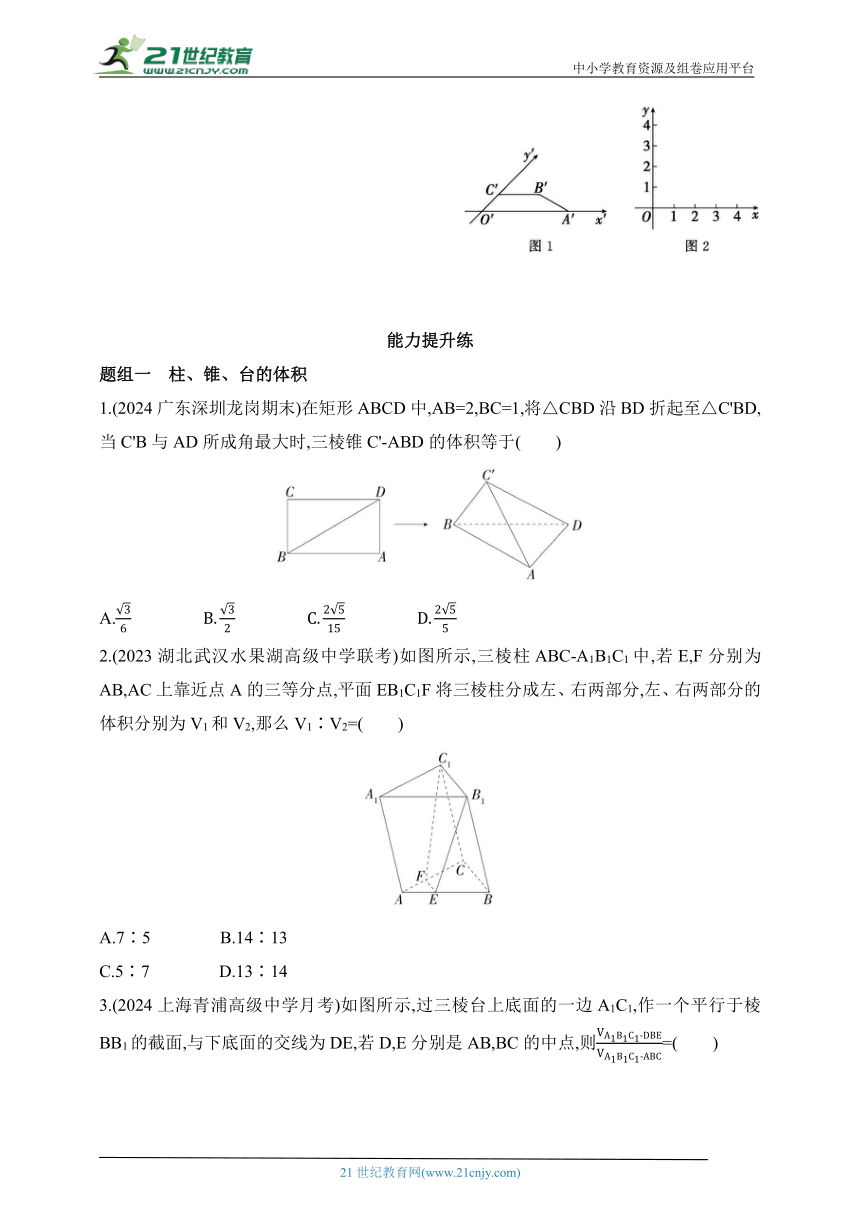
12.(2024河南新乡多校期中联考)如图1所示,四边形O'A'B'C'为水平放置的四边形OABC的斜二测直观图,其中∠x'O'y'=45°,O'A'=4,O'C'=1,B'C'=2.
(1)在图2所示的直角坐标系中画出四边形OABC,并求四边形OABC的面积;
(2)若将四边形OABC以直线OA为轴旋转一周,求旋转形成的几何体的体积及表面积.
能力提升练
题组一 柱、锥、台的体积
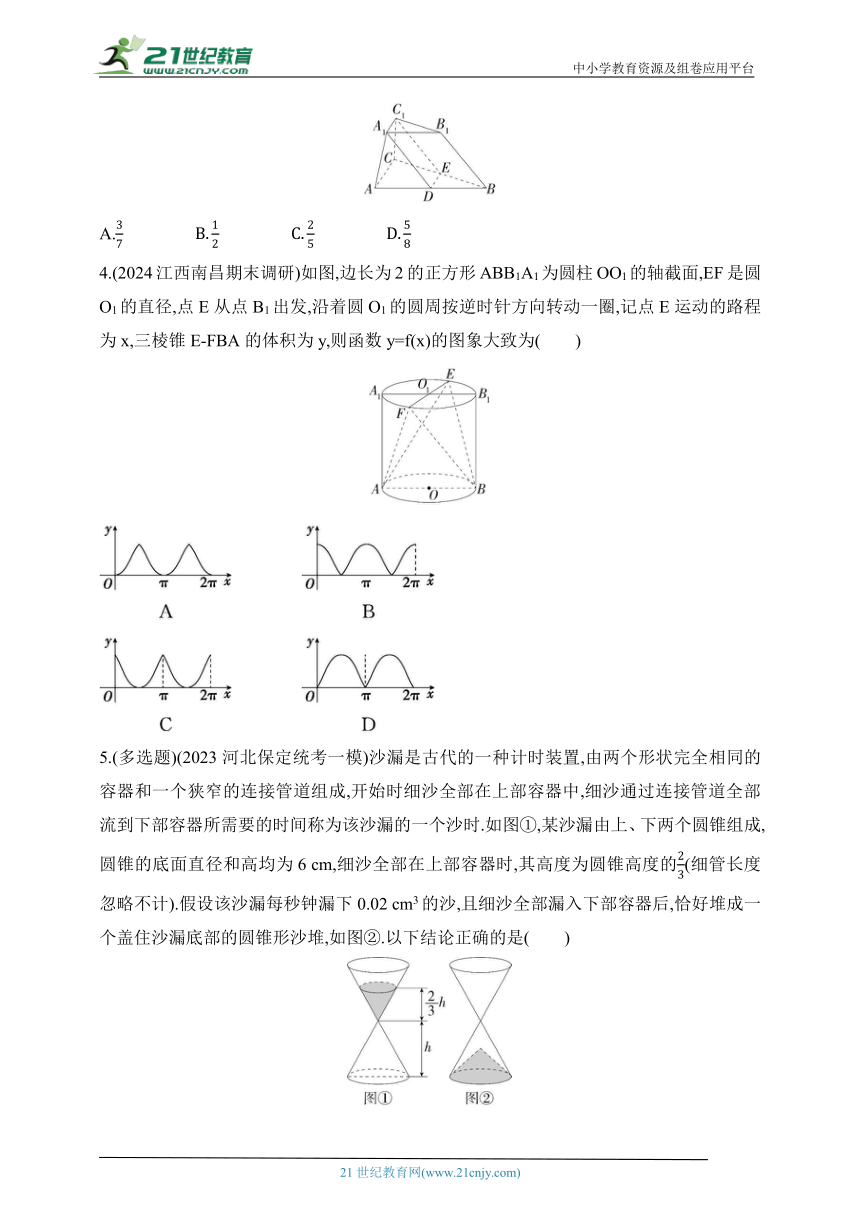
1.(2024广东深圳龙岗期末)在矩形ABCD中,AB=2,BC=1,将△CBD沿BD折起至△C'BD,当C'B与AD所成角最大时,三棱锥C'-ABD的体积等于( )
A.
2.(2023湖北武汉水果湖高级中学联考)如图所示,三棱柱ABC-A1B1C1中,若E,F分别为AB,AC上靠近点A的三等分点,平面EB1C1F将三棱柱分成左、右两部分,左、右两部分的体积分别为V1和V2,那么V1∶V2=( )
A.7∶5 B.14∶13
C.5∶7 D.13∶14
3.(2024上海青浦高级中学月考)如图所示,过三棱台上底面的一边A1C1,作一个平行于棱BB1的截面,与下底面的交线为DE,若D,E分别是AB,BC的中点,则=( )
A.
4.(2024江西南昌期末调研)如图,边长为2的正方形ABB1A1为圆柱OO1的轴截面,EF是圆O1的直径,点E从点B1出发,沿着圆O1的圆周按逆时针方向转动一圈,记点E运动的路程为x,三棱锥E-FBA的体积为y,则函数y=f(x)的图象大致为( )
5.(多选题)(2023河北保定统考一模)沙漏是古代的一种计时装置,由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时.如图①,某沙漏由上、下两个圆锥组成,圆锥的底面直径和高均为6 cm,细沙全部在上部容器时,其高度为圆锥高度的(细管长度忽略不计).假设该沙漏每秒钟漏下0.02 cm3的沙,且细沙全部漏入下部容器后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,如图②.以下结论正确的是( )
A.沙漏的侧面积是9π cm2
B.沙漏中的细沙体积为 cm3
C.细沙全部漏入下部容器后的圆锥形沙堆的高约为2.4 cm
D.该沙漏的一个沙时大约是837秒(π≈3.14)
6.(2024上海宝山模拟)如图,已知点P在圆柱OO1的底面圆O的圆周上,AB为圆O的直径.
(1)求证:BP⊥A1P;
(2)若OA=2,∠BOP=60°,圆柱的体积为16π,求异面直线AP与A1B夹角的大小.
7.(2024福建莆田五中期中)正三棱柱ABC-A1B1C1的底面正三角形的边长为2,D为BC的中点,AA1=3.
(1)证明:A1B∥平面ADC1;
(2)求C到平面AC1D的距离.
题组二 组合体的表面积和体积
8.(多选题)(2024浙江杭州外国语学校期中)
《九章算术》中记载了一种称为“曲池”的几何体,该几何体是上、下底面均为扇环形的柱体(扇环是指圆环被扇形截得的部分).现有一个如图所示的曲池,AA1垂直于底面,AA1=5,底面扇环所对的圆心角为,弧AD的长度是弧BC长度的3倍,CD=2,则下列说法正确的是( )
A.弧AD的长度为
B.曲池的体积为
C.曲池的表面积为20+14π
D.三棱锥A-CC1D的体积为5
9.(2023广东揭阳三校联考)如图,一个圆锥挖掉一个内接正三棱柱ABC-A1B1C1(该棱柱的各个顶点均在圆锥的侧面上),且棱柱的侧面ABB1A1落在圆锥的底面上,已知该正三棱柱的底面边长为6,高为8.
(1)求挖掉的正三棱柱ABC-A1B1C1的体积;
(2)求剩余几何体的体积和表面积.
答案与分层梯度式解析
第六章 立体几何初步
§6 简单几何体的再认识
6.2 柱、锥、台的体积
基础过关练
1.A 由题意得圆锥的母线长为1,设圆锥的底面半径为r,高为h,底面积为S,
则2πr=π,∴r=,∴h=,
故圆锥的体积V=,
故选A.
2.C 设圆柱底面半径为r,
在△ABC中,由正弦定理得2r=,解得r=,
故圆柱的高h=,
所以圆柱的体积V=πr2h=π×.
3.D 如图,几何体ABCD-A1B1C1D1为正四棱台,AB=2,A1B1=4,AA1=2.
在等腰梯形A1B1BA中,过点A作AE⊥A1B1,垂足为E,则A1E=.
连接AC,A1C1,
易得AC=,
过点A作AG⊥A1C1,垂足为G,则AG的长为该正四棱台的高,
则A1G=,
∴正四棱台的体积V=×h=.
4.BCD 作BE⊥CD于E,则CE==1(cm),则BE=(cm),则圆台的高为 cm,A错误;
圆台的轴截面面积为×(2+4)×(cm2),B正确;
圆台的侧面积为π×(1+2)×2=6π(cm2),C正确;
圆台的体积为×(π+4π+(cm3),D正确.
故选BCD.
5.答案
解析 设三棱台ABC-A1B1C1的高为h,
则V=)h,可得h=,
所以S1·,
因为S1∶S2=1∶4,
所以·S1·V.
6.解析 (1)证明:连接AC,记AC∩BD=O,连接OE,则O为AC的中点,
∵E为PA的中点,∴OE是△ACP的中位线,
∴OE∥PC,
又∵OE 平面BDE,PC 平面BDE,
∴PC∥平面BDE.
(2)∵PD⊥平面ABCD,
∴PC与平面ABCD的夹角为∠PCD,即∠PCD=,
∴△PCD为等腰直角三角形,
∴PD=CD=4,
易得点E到平面ABCD的距离h=,
∴VC-BDE=VE-BCD=S△BCD·h=BC·CD·h=×4×4×.
7.解析 (1)如图,过点P作PO⊥底面ABCD于点O,PO交平面A1B1C1D1于点O1,故O为底面ABCD的中心,
则O1O=PO-PO1=×PO1-PO1=PO1=4,
即棱台A1B1C1D1-ABCD的高O1O=4,
故×[]×4=×56×4=.
(2)连接OA,则AO=×4,
过A1作A1M⊥AB于点M,则A1M=,
故=S正方形ABCD+
=+4××(2)×3
=32+8+72=112.
8.答案 3
解析 设圆锥的底面半径为R,由题意得,V水=π·32·h=·π·R2·h,解得R=3(负值舍去).
9.答案
解析 由题意得,正六棱锥的底面边长为1,所以正六棱锥的高为=1,正六棱锥的底面面积为6××12=,所以此组合体的体积为×2+×1=.
10.答案 10π
解析 用一个完全相同的几何体将题中几何体补成一个圆柱,如图,则圆柱的体积为π×22×(2+3)=20π,故所求几何体的体积为10π.
11.答案 (36-6π)cm3
解析 根据题意,得×6=36(cm3).
设圆柱的底面半径为r cm,高为h cm,
则r==1,
故V圆柱=πr2h=6π(cm3),
所以剩余部分的几何体的体积V=-V圆柱=(36-6π) cm3.
12.解析 (1)在直观图中,O'A'=4,O'C'=1,B'C'=2,
则在四边形OABC中,OA=O'A'=4,OC=2O'C'=2,
BC=B'C'=2,OC⊥OA,
所以四边形OABC如图所示,
由图可知,四边形OABC为直角梯形,其面积为=6.
(2)将直角梯形OABC以直线OA为轴旋转一周,所形成的几何体由一个圆柱和一个同底的圆锥组成,
由(1)可知几何体的底面半径r=2,圆柱的高h1=2,圆锥的高h2=2,圆锥的母线长l=,
所以该几何体的体积V=V圆柱+V圆锥=πr2h1+πr2h2=8π+,
表面积S=πr2+2πrh1+πrl=4π+8π+4π=(12+4)π.
能力提升练
1.A 因为异面直线所成角的范围是,故当C'B⊥AD时,C'B与AD所成角最大,
因为四边形ABCD是矩形,所以AB⊥AD,
因为AB∩C'B=B,AB,C'B 平面ABC',
所以AD⊥平面ABC',
因为AC' 平面ABC',所以AD⊥AC',
在直角三角形ADC'中,AC'=,
所以BC'2+AC'2=AB2,所以BC'⊥AC',
所以VC'-ABD=VD-ABC'=S△ABC'·AD=×1××1=.故选A.
2.D 设三棱柱的高为h,一个底面的面积为S,体积为V,则V=V1+V2=Sh,
因为E,F分别为AB,AC上靠近点A的三等分点,
所以S△AEF=S,
则V1=Sh,
所以V2=V-V1=Sh,所以V1∶V2=13∶14.故选D.
3.A 因为BB1∥平面A1C1ED,平面BCC1B1∩平面A1C1ED=C1E,平面ABB1A1∩平面A1C1ED=A1D,所以BB1∥A1D,BB1∥C1E,
因为平面A1B1C1∥平面ABC,平面A1B1C1∩平面A1C1ED=A1C1,平面ABC∩平面A1C1ED=DE,所以A1C1∥DE,
故几何体A1B1C1-DBE为棱柱,设棱柱的高为h,
故=S△BDE·h,
又D,E分别是AB,BC的中点,所以S△ABC=4S△BDE,
所以(S△BDE+S△ABC+S△BDE·h,故,故选A.
4.D 连接O1A,O1B,把三棱锥E-FBA分成三棱锥E-O1AB和三棱锥F-O1AB,则这两个三棱锥的体积相等,所以VE-FBA=2,
设点F到平面O1AB的距离为h,根据题意可得h=sin x,x∈[0,2π],
易知△O1AB的边AB上的高为2,
所以×2×2=2,
所以VE-FBA=2=2××2×sin x=sin x,x∈[0,2π].
当点E从点B1出发,沿着圆O1按逆时针方向转动通过A1时,在x∈(π,2π)内的体积变化情况与在[0,π]内的体积变化情况一致.
故选D.
5.BD A选项,设下圆锥的母线长为l,则l=(cm),
故下圆锥的侧面积S=3×3π=9π(cm2),故沙漏的侧面积为2S=18π cm2,故A错误;
B选项,当细沙全部在上部容器时,其高度为圆锥高度的,所以细沙形成的圆锥的底面半径为×3=2(cm),高为6×=4(cm),故细沙形成的圆锥的底面积为π×22=4π(cm2),所以沙漏中的细沙体积为×4π×4=(cm3),故B正确;
C选项,由B选项可知,细沙全部漏入下部容器后的圆锥形沙堆的体积为 cm3,此圆锥形沙堆的底面积为π×32=9π(cm2),故其高为≈1.8(cm),故C错误;
D选项,÷0.02≈≈837(秒),故该沙漏的一个沙时大约是837秒,故D正确.
故选BD.
6.解析 (1)证明:易知AP⊥BP,由AA1⊥平面PAB,BP 平面PAB,得AA1⊥BP,
因为AP∩AA1=A,AP,AA1 平面PAA1,所以BP⊥平面PAA1,又A1P 平面PAA1,所以BP⊥A1P.
(2)如图,延长PO交圆O于点Q,连接BQ,A1Q,AQ,
易知BQ∥AP,则∠A1BQ(或其补角)即为异面直线AP与A1B的夹角,
由题知V圆柱=π·OA2·AA1=4π·AA1=16π,解得AA1=4,
易得BQ=AP=2,
在△A1BQ中,由余弦定理得cos∠A1BQ=,
又0<∠A1BQ<π,所以∠A1BQ=60°,
所以异面直线AP与A1B的夹角为60°.
7.解析 (1)证明:连接A1C,设A1C∩AC1=E,连接DE.
易知四边形ACC1A1为矩形,则E是A1C的中点,
所以DE是△CA1B的中位线,所以DE∥A1B,
又A1B 平面ADC1,DE 平面ADC1,
所以A1B∥平面ADC1.
(2)由题意得BC=2,AD=ABsin 60°=,
故S△ADC=AD·DC=×1=,
因为CC1⊥平面ABC,CC1=AA1=3,
所以S△ADC·CC1=×3=,
由正三棱柱的性质可知,平面ABC⊥平面BCC1B1,平面ABC∩平面BCC1B1=BC,又AD⊥BC,AD 平面ABC,所以AD⊥平面BCC1B1,
因为C1D 平面BCC1B1,所以AD⊥C1D,
易知C1D=,所以AD·C1D=,
设点C到平面AC1D的距离为d,
由,得,解得d=,
所以点C到平面AC1D的距离为.
方法总结 在立体几何中求点到平面的距离时,若该距离可视为某三棱锥的一条高时,通常用等体积法求距离.
8.ACD 设弧AD所在圆的半径为R,弧BC所在圆的半径为r,
∵弧AD的长度是弧BC长度的3倍,∴R=3×r,即R=3r,∴CD=R-r=2r=2,∴r=1,R=3,
∴弧AD的长度为,故A正确;
曲池的体积为×AA1=π×32-π×12×5=10π,故B错误;
曲池的表面积为×2+×5+2×5×2=×2+×3+×1×5+20=20+14π,故C正确;
×2×3×5=5,故D正确.
故选ACD.
9.解析 (1)由题意可知,正三棱柱ABC-A1B1C1的底面积S△ABC=×6×6×,高AA1=8,
∴×8=72.
(2)如图,过点V,C,C1作圆锥的轴截面VEF,分别交AB,A1B1于点M,N,连接A1B.
由题可知☉O是矩形ABB1A1的外接圆,
∵BB1=8,AB=6,
∴A1B==10,即☉O的半径为5.
∵ON=EF=5,∴NF=1,
∵C1N=,且△FC1N与△FVO相似,
∴,即,∴VO=15,
∴VF=,
∴V圆锥=×25π×15π,
则剩余几何体的体积为125π-72.
易得圆锥的侧面积为10×5π=50π,底面积为25π,
∴剩余几何体的表面积为50π+25π-6×8+6×8×2+9×2=(50+25)π+48+18.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025北师大版高中数学必修第二册
6.2 柱、锥、台的体积
基础过关练
题组一 柱、锥、台的体积
1.(2022江苏南通阶段练习)一个圆锥的侧面展开图恰好是一个半径为1的半圆,则该圆锥的体积为( )
A.π
2.(2024浙江三锋教研联盟期中)如图,四面体P-ABC的各个面都是边长为2的正三角形,其中顶点A,B,C在一个圆柱的下底面圆周上,顶点P是上底面圆的圆心,则圆柱的体积是( )
A.π
3.(2023广东广州天河中学期中)正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为( )
A.20+12
4.(多选题)(2024广东惠州模拟)某班级到一工厂劳动实践,加工出如图所示的圆台O1O2,在轴截面ABCD中,AB=AD=BC=2 cm,且CD=2AB,则( )
A.该圆台的高为1 cm
B.该圆台的轴截面面积为3 cm2
C.该圆台的侧面积为6π cm2
D.该圆台的体积为 cm3
5.(2024江西南昌第十九中学等校期末调研测试)如图,已知三棱台ABC-A1B1C1的体积为V,记上、下底面面积分别为S1,S2,若S1∶S2=1∶4,则三棱锥B-A1B1C1的体积为 V.
6.(2024江西赣州期末)如图,在四棱锥P-ABCD中,四边形ABCD是边长为4的正方形,PD⊥平面ABCD,PC与平面ABCD的夹角为,E为PA上的点.
(1)若E为PA的中点,证明:PC∥平面BDE;
(2)若E为PA上靠近A的三等分点,求三棱锥C-BDE的体积.
7.(2024安徽合肥一中期中)如图所示,底面边长为4的正四棱锥P-ABCD被平行于底面的平面所截,截去一个底面边长为2,高为4的正四棱锥P-A1B1C1D1.
(1)求棱台A1B1C1D1-ABCD的体积;
(2)求棱台A1B1C1D1-ABCD的表面积.
题组二 组合体的体积
8.(2023天津河东一模)有一个由圆锥和圆柱组成的玻璃容器,其中间连通(玻璃壁厚度忽略不计),容器中装有一定体积的水,圆柱高为10,底面半径为3,圆锥高为h,底面半径大于圆柱,图1中,圆柱在下面,液面保持水平,高度为h,将容器倒置如图2所示,若水恰好充满圆锥,则圆锥的底面半径为 .
9.(2022山西运城联考)为了给热爱朗读的师生提供一个安静、独立的环境,某学校修建了若干“朗读亭”.如图所示,该朗读亭的外形是一个正六棱柱和正六棱锥的组合体,过正六棱柱两条相对侧棱的截面为正方形,若正六棱锥的侧棱长为,正六棱柱的高为2,则此组合体的体积为 .
10.如图,一个底面半径为2的圆柱被一平面所截,截得的几何体的最短和最长母线长分别为2和3,则该几何体的体积为 .
11.(2023吉林长春二中期中)如图,三棱柱ABC-A1B1C1的侧棱垂直于底面,其高为6 cm,底面三角形的边长分别为3 cm,4 cm,5 cm,以上、下底面的内切圆为底面,挖去一个圆柱,则剩余部分的几何体的体积为 .
12.(2024河南新乡多校期中联考)如图1所示,四边形O'A'B'C'为水平放置的四边形OABC的斜二测直观图,其中∠x'O'y'=45°,O'A'=4,O'C'=1,B'C'=2.
(1)在图2所示的直角坐标系中画出四边形OABC,并求四边形OABC的面积;
(2)若将四边形OABC以直线OA为轴旋转一周,求旋转形成的几何体的体积及表面积.
能力提升练
题组一 柱、锥、台的体积
1.(2024广东深圳龙岗期末)在矩形ABCD中,AB=2,BC=1,将△CBD沿BD折起至△C'BD,当C'B与AD所成角最大时,三棱锥C'-ABD的体积等于( )
A.
2.(2023湖北武汉水果湖高级中学联考)如图所示,三棱柱ABC-A1B1C1中,若E,F分别为AB,AC上靠近点A的三等分点,平面EB1C1F将三棱柱分成左、右两部分,左、右两部分的体积分别为V1和V2,那么V1∶V2=( )
A.7∶5 B.14∶13
C.5∶7 D.13∶14
3.(2024上海青浦高级中学月考)如图所示,过三棱台上底面的一边A1C1,作一个平行于棱BB1的截面,与下底面的交线为DE,若D,E分别是AB,BC的中点,则=( )
A.
4.(2024江西南昌期末调研)如图,边长为2的正方形ABB1A1为圆柱OO1的轴截面,EF是圆O1的直径,点E从点B1出发,沿着圆O1的圆周按逆时针方向转动一圈,记点E运动的路程为x,三棱锥E-FBA的体积为y,则函数y=f(x)的图象大致为( )
5.(多选题)(2023河北保定统考一模)沙漏是古代的一种计时装置,由两个形状完全相同的容器和一个狭窄的连接管道组成,开始时细沙全部在上部容器中,细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时.如图①,某沙漏由上、下两个圆锥组成,圆锥的底面直径和高均为6 cm,细沙全部在上部容器时,其高度为圆锥高度的(细管长度忽略不计).假设该沙漏每秒钟漏下0.02 cm3的沙,且细沙全部漏入下部容器后,恰好堆成一个盖住沙漏底部的圆锥形沙堆,如图②.以下结论正确的是( )
A.沙漏的侧面积是9π cm2
B.沙漏中的细沙体积为 cm3
C.细沙全部漏入下部容器后的圆锥形沙堆的高约为2.4 cm
D.该沙漏的一个沙时大约是837秒(π≈3.14)
6.(2024上海宝山模拟)如图,已知点P在圆柱OO1的底面圆O的圆周上,AB为圆O的直径.
(1)求证:BP⊥A1P;
(2)若OA=2,∠BOP=60°,圆柱的体积为16π,求异面直线AP与A1B夹角的大小.
7.(2024福建莆田五中期中)正三棱柱ABC-A1B1C1的底面正三角形的边长为2,D为BC的中点,AA1=3.
(1)证明:A1B∥平面ADC1;
(2)求C到平面AC1D的距离.
题组二 组合体的表面积和体积
8.(多选题)(2024浙江杭州外国语学校期中)
《九章算术》中记载了一种称为“曲池”的几何体,该几何体是上、下底面均为扇环形的柱体(扇环是指圆环被扇形截得的部分).现有一个如图所示的曲池,AA1垂直于底面,AA1=5,底面扇环所对的圆心角为,弧AD的长度是弧BC长度的3倍,CD=2,则下列说法正确的是( )
A.弧AD的长度为
B.曲池的体积为
C.曲池的表面积为20+14π
D.三棱锥A-CC1D的体积为5
9.(2023广东揭阳三校联考)如图,一个圆锥挖掉一个内接正三棱柱ABC-A1B1C1(该棱柱的各个顶点均在圆锥的侧面上),且棱柱的侧面ABB1A1落在圆锥的底面上,已知该正三棱柱的底面边长为6,高为8.
(1)求挖掉的正三棱柱ABC-A1B1C1的体积;
(2)求剩余几何体的体积和表面积.
答案与分层梯度式解析
第六章 立体几何初步
§6 简单几何体的再认识
6.2 柱、锥、台的体积
基础过关练
1.A 由题意得圆锥的母线长为1,设圆锥的底面半径为r,高为h,底面积为S,
则2πr=π,∴r=,∴h=,
故圆锥的体积V=,
故选A.
2.C 设圆柱底面半径为r,
在△ABC中,由正弦定理得2r=,解得r=,
故圆柱的高h=,
所以圆柱的体积V=πr2h=π×.
3.D 如图,几何体ABCD-A1B1C1D1为正四棱台,AB=2,A1B1=4,AA1=2.
在等腰梯形A1B1BA中,过点A作AE⊥A1B1,垂足为E,则A1E=.
连接AC,A1C1,
易得AC=,
过点A作AG⊥A1C1,垂足为G,则AG的长为该正四棱台的高,
则A1G=,
∴正四棱台的体积V=×h=.
4.BCD 作BE⊥CD于E,则CE==1(cm),则BE=(cm),则圆台的高为 cm,A错误;
圆台的轴截面面积为×(2+4)×(cm2),B正确;
圆台的侧面积为π×(1+2)×2=6π(cm2),C正确;
圆台的体积为×(π+4π+(cm3),D正确.
故选BCD.
5.答案
解析 设三棱台ABC-A1B1C1的高为h,
则V=)h,可得h=,
所以S1·,
因为S1∶S2=1∶4,
所以·S1·V.
6.解析 (1)证明:连接AC,记AC∩BD=O,连接OE,则O为AC的中点,
∵E为PA的中点,∴OE是△ACP的中位线,
∴OE∥PC,
又∵OE 平面BDE,PC 平面BDE,
∴PC∥平面BDE.
(2)∵PD⊥平面ABCD,
∴PC与平面ABCD的夹角为∠PCD,即∠PCD=,
∴△PCD为等腰直角三角形,
∴PD=CD=4,
易得点E到平面ABCD的距离h=,
∴VC-BDE=VE-BCD=S△BCD·h=BC·CD·h=×4×4×.
7.解析 (1)如图,过点P作PO⊥底面ABCD于点O,PO交平面A1B1C1D1于点O1,故O为底面ABCD的中心,
则O1O=PO-PO1=×PO1-PO1=PO1=4,
即棱台A1B1C1D1-ABCD的高O1O=4,
故×[]×4=×56×4=.
(2)连接OA,则AO=×4,
过A1作A1M⊥AB于点M,则A1M=,
故=S正方形ABCD+
=+4××(2)×3
=32+8+72=112.
8.答案 3
解析 设圆锥的底面半径为R,由题意得,V水=π·32·h=·π·R2·h,解得R=3(负值舍去).
9.答案
解析 由题意得,正六棱锥的底面边长为1,所以正六棱锥的高为=1,正六棱锥的底面面积为6××12=,所以此组合体的体积为×2+×1=.
10.答案 10π
解析 用一个完全相同的几何体将题中几何体补成一个圆柱,如图,则圆柱的体积为π×22×(2+3)=20π,故所求几何体的体积为10π.
11.答案 (36-6π)cm3
解析 根据题意,得×6=36(cm3).
设圆柱的底面半径为r cm,高为h cm,
则r==1,
故V圆柱=πr2h=6π(cm3),
所以剩余部分的几何体的体积V=-V圆柱=(36-6π) cm3.
12.解析 (1)在直观图中,O'A'=4,O'C'=1,B'C'=2,
则在四边形OABC中,OA=O'A'=4,OC=2O'C'=2,
BC=B'C'=2,OC⊥OA,
所以四边形OABC如图所示,
由图可知,四边形OABC为直角梯形,其面积为=6.
(2)将直角梯形OABC以直线OA为轴旋转一周,所形成的几何体由一个圆柱和一个同底的圆锥组成,
由(1)可知几何体的底面半径r=2,圆柱的高h1=2,圆锥的高h2=2,圆锥的母线长l=,
所以该几何体的体积V=V圆柱+V圆锥=πr2h1+πr2h2=8π+,
表面积S=πr2+2πrh1+πrl=4π+8π+4π=(12+4)π.
能力提升练
1.A 因为异面直线所成角的范围是,故当C'B⊥AD时,C'B与AD所成角最大,
因为四边形ABCD是矩形,所以AB⊥AD,
因为AB∩C'B=B,AB,C'B 平面ABC',
所以AD⊥平面ABC',
因为AC' 平面ABC',所以AD⊥AC',
在直角三角形ADC'中,AC'=,
所以BC'2+AC'2=AB2,所以BC'⊥AC',
所以VC'-ABD=VD-ABC'=S△ABC'·AD=×1××1=.故选A.
2.D 设三棱柱的高为h,一个底面的面积为S,体积为V,则V=V1+V2=Sh,
因为E,F分别为AB,AC上靠近点A的三等分点,
所以S△AEF=S,
则V1=Sh,
所以V2=V-V1=Sh,所以V1∶V2=13∶14.故选D.
3.A 因为BB1∥平面A1C1ED,平面BCC1B1∩平面A1C1ED=C1E,平面ABB1A1∩平面A1C1ED=A1D,所以BB1∥A1D,BB1∥C1E,
因为平面A1B1C1∥平面ABC,平面A1B1C1∩平面A1C1ED=A1C1,平面ABC∩平面A1C1ED=DE,所以A1C1∥DE,
故几何体A1B1C1-DBE为棱柱,设棱柱的高为h,
故=S△BDE·h,
又D,E分别是AB,BC的中点,所以S△ABC=4S△BDE,
所以(S△BDE+S△ABC+S△BDE·h,故,故选A.
4.D 连接O1A,O1B,把三棱锥E-FBA分成三棱锥E-O1AB和三棱锥F-O1AB,则这两个三棱锥的体积相等,所以VE-FBA=2,
设点F到平面O1AB的距离为h,根据题意可得h=sin x,x∈[0,2π],
易知△O1AB的边AB上的高为2,
所以×2×2=2,
所以VE-FBA=2=2××2×sin x=sin x,x∈[0,2π].
当点E从点B1出发,沿着圆O1按逆时针方向转动通过A1时,在x∈(π,2π)内的体积变化情况与在[0,π]内的体积变化情况一致.
故选D.
5.BD A选项,设下圆锥的母线长为l,则l=(cm),
故下圆锥的侧面积S=3×3π=9π(cm2),故沙漏的侧面积为2S=18π cm2,故A错误;
B选项,当细沙全部在上部容器时,其高度为圆锥高度的,所以细沙形成的圆锥的底面半径为×3=2(cm),高为6×=4(cm),故细沙形成的圆锥的底面积为π×22=4π(cm2),所以沙漏中的细沙体积为×4π×4=(cm3),故B正确;
C选项,由B选项可知,细沙全部漏入下部容器后的圆锥形沙堆的体积为 cm3,此圆锥形沙堆的底面积为π×32=9π(cm2),故其高为≈1.8(cm),故C错误;
D选项,÷0.02≈≈837(秒),故该沙漏的一个沙时大约是837秒,故D正确.
故选BD.
6.解析 (1)证明:易知AP⊥BP,由AA1⊥平面PAB,BP 平面PAB,得AA1⊥BP,
因为AP∩AA1=A,AP,AA1 平面PAA1,所以BP⊥平面PAA1,又A1P 平面PAA1,所以BP⊥A1P.
(2)如图,延长PO交圆O于点Q,连接BQ,A1Q,AQ,
易知BQ∥AP,则∠A1BQ(或其补角)即为异面直线AP与A1B的夹角,
由题知V圆柱=π·OA2·AA1=4π·AA1=16π,解得AA1=4,
易得BQ=AP=2,
在△A1BQ中,由余弦定理得cos∠A1BQ=,
又0<∠A1BQ<π,所以∠A1BQ=60°,
所以异面直线AP与A1B的夹角为60°.
7.解析 (1)证明:连接A1C,设A1C∩AC1=E,连接DE.
易知四边形ACC1A1为矩形,则E是A1C的中点,
所以DE是△CA1B的中位线,所以DE∥A1B,
又A1B 平面ADC1,DE 平面ADC1,
所以A1B∥平面ADC1.
(2)由题意得BC=2,AD=ABsin 60°=,
故S△ADC=AD·DC=×1=,
因为CC1⊥平面ABC,CC1=AA1=3,
所以S△ADC·CC1=×3=,
由正三棱柱的性质可知,平面ABC⊥平面BCC1B1,平面ABC∩平面BCC1B1=BC,又AD⊥BC,AD 平面ABC,所以AD⊥平面BCC1B1,
因为C1D 平面BCC1B1,所以AD⊥C1D,
易知C1D=,所以AD·C1D=,
设点C到平面AC1D的距离为d,
由,得,解得d=,
所以点C到平面AC1D的距离为.
方法总结 在立体几何中求点到平面的距离时,若该距离可视为某三棱锥的一条高时,通常用等体积法求距离.
8.ACD 设弧AD所在圆的半径为R,弧BC所在圆的半径为r,
∵弧AD的长度是弧BC长度的3倍,∴R=3×r,即R=3r,∴CD=R-r=2r=2,∴r=1,R=3,
∴弧AD的长度为,故A正确;
曲池的体积为×AA1=π×32-π×12×5=10π,故B错误;
曲池的表面积为×2+×5+2×5×2=×2+×3+×1×5+20=20+14π,故C正确;
×2×3×5=5,故D正确.
故选ACD.
9.解析 (1)由题意可知,正三棱柱ABC-A1B1C1的底面积S△ABC=×6×6×,高AA1=8,
∴×8=72.
(2)如图,过点V,C,C1作圆锥的轴截面VEF,分别交AB,A1B1于点M,N,连接A1B.
由题可知☉O是矩形ABB1A1的外接圆,
∵BB1=8,AB=6,
∴A1B==10,即☉O的半径为5.
∵ON=EF=5,∴NF=1,
∵C1N=,且△FC1N与△FVO相似,
∴,即,∴VO=15,
∴VF=,
∴V圆锥=×25π×15π,
则剩余几何体的体积为125π-72.
易得圆锥的侧面积为10×5π=50π,底面积为25π,
∴剩余几何体的表面积为50π+25π-6×8+6×8×2+9×2=(50+25)π+48+18.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
