北师大八上1.1.1探索勾股定理

(共28张PPT)
第一章 勾股定理
1.1.1探索勾股定理
北师大版 数学 八年级 上册
学习目标
1.通过数格子的方法探索勾股定理；学生理解勾股定理反映的是直角三角形三边之间的数量关系。
2.在探索过程中，学生经历了“观察-猜想-归纳”的教学过程，将形与数密切联系起来。
3.初步运用勾股定理进行简单的计算和实际的应用。
情景导入
我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦.图1-1称为“弦图”，最早是由三国时期的数学家赵爽在为《周髀算经》作法时给出的.图1-2是在北京召开的2002年国际数学家大会（TCM－2002）的会标，其图案正是“弦图”，它标志着中国古代的数学成就.
　　　　　　　
图1-1
图1-2
情景导入
相传 2500 多年前，毕达哥拉斯有一次在朋友家做客时，发现朋友家用砖铺成的地面图案反映了直角三角形三边的某种数量关系.
请你观察一下地面的图案，从中发现了什么？
探索新知
勾股定理的初步认识
一
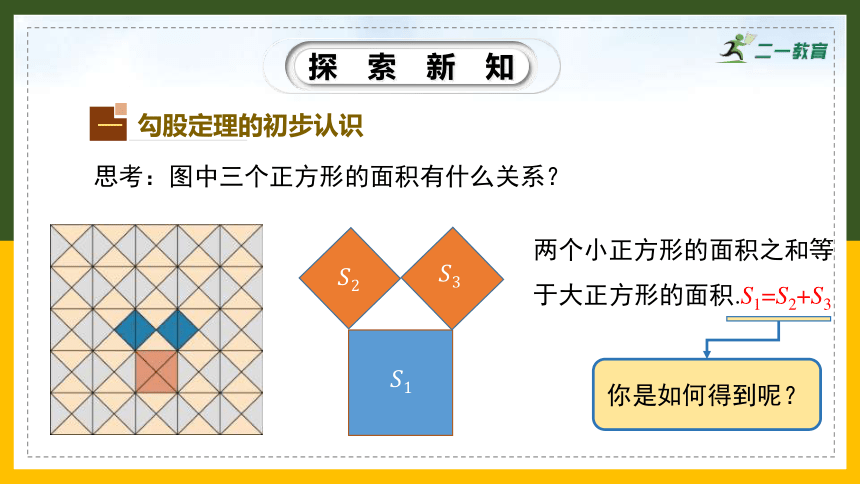
思考：图中三个正方形的面积有什么关系？
两个小正方形的面积之和等于大正方形的面积.S1=S2+S3
你是如何得到呢？
探索新知
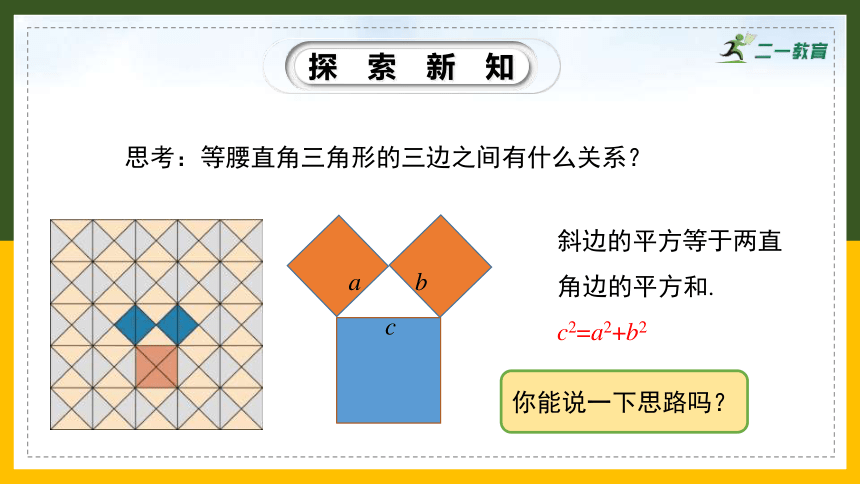
思考：等腰直角三角形的三边之间有什么关系？
斜边的平方等于两直角边的平方和.
c2=a2+b2
a
b
c
你能说一下思路吗？
探索新知
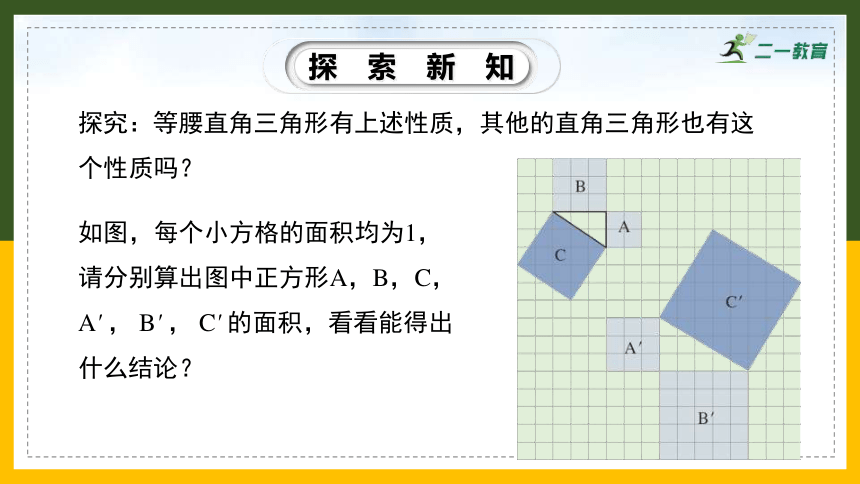
探究：等腰直角三角形有上述性质，其他的直角三角形也有这个性质吗？
如图，每个小方格的面积均为1，请分别算出图中正方形A，B，C， A' ， B' ， C' 的面积，看看能得出什么结论？
探索新知
A B C A' B' C'
面积/格
4
34
25
9
13
9
你发现了什么规律吗？
我发现 SA+SB=SC，SA'+SB'=SC'
探索新知
勾股定理刻画了直角三角形三边的平方关系，你能用语言描述吗？
我国古代学者把直角三角形较短的直角边称为“勾”，较长的直角边称为“股”，斜边称为“弦”.通过以上
探索可以发现：
即
c
b
a
总结归纳
探索新知
勾股定理：
在直角三角形中，两条直角边的平方和等于斜边的平方.
在Rt△ABC中，直角边分别是a，b，斜边是c，则：
c
b
a
几何语言：
∵在Rt△ABC中 ，∠C=90°，
∴a2+b2=c2（勾股定理）.
a、b、c可以为负值吗？
B
C
A
a（勾）
c（弦）
b（股）
探索新知
注意：1.勾股定理是直角三角形的特殊性质，所以其适用的前提是直角三角形.
2.运用勾股定理时，一定要分清直角边和斜边，若没有明确哪条边是斜边，则需要分类讨论，写出所有可能的情况，以避免漏解或者错解.
探索新知
练一练
探索新知
判断：
1.若△ABC的三条边分别为a，b，c，
则a +b =c ( )
2.若△ABC的a=6，b=8，则c=10 ( )
3.若a，b，c 分别是△ABC的三条边的长，∠A=90°，则b +c =a （ ）


√
探索新知
利用勾股定理进行计算
二
例1：分别以直角三角形三边为边长的正方形的面积如下图，问另外一个正方形的面积.
625
144
81
B
225
∟
225
400
A
∟
规律：以直角三角形两直角边为边长的正方形的面积和等于以斜边长的正方形面积。
探索新知
例2：如图，图中所有的三角形都是直角三角形，四边形都是正方形.已知正方形 A，B，C，D 的边长分别为12，16，9，12，求最大正方形 E 的面积.
探索新知
解：设另两个正方形中大的为M，小的为N，
由勾股定理和正方形的面积公式，
得，
而
探索新知
例3： 如果直角三角形两直角边长分别为 BC=5厘米,AC=12厘米,求斜边AB的长度.
a
b
c
A
C
B
解：在Rt△ABC中根据勾股定理,
AC +BC =AB ，
AC=12，BC=5
所以12 +5 =AB ，
所以AB =12 +5 =169，
所以AB=13厘米.
答：斜边AB的长度为13厘米.
例4：我方侦查员小王在距离东西向公路400m处侦查，发现一辆敌方汽车在公路疾驶，他赶紧拿出红外测距仪，测得汽车与他相距400m，10s后，汽车与他相距500m，你能帮小王计算敌方汽车的速度吗？
解:由勾股定理，可以得到AB2=BC2+AC2，也就是5002=BC2+4002，所以BC=300.
敌方汽车10s行驶了300m，那么它1h行驶的距离为300×6×60=108000（m），即它行驶的速度为108km/h
公路
C
B
400m
500m
A
探索新知
当堂检测
1．(1)如图，所有的四边形都是正方形，三角形是直角三角形，其中最大的正方形的面积为25，则正方形A，B的面积的和为　 　．
　25　
第(1)题图
当堂检测
(2)(北师八上P17)如图，在△ABC中，∠A＝90°，则三个半圆面积S1，S2，S3的关系为　 　．
　S1＝S2＋S3　
第(2)题图
当堂检测
小结：在勾股定理的使用中须牢记1~25的平方数.
2．如图，在Rt△ABC中，∠C＝90°．
(1)若a＝3，b＝4，则c＝　 　；
(2)若b＝8，c＝10，则a＝　 　；
(3)若a＝5，b＝12，则c＝　 　．
　13　
　6　
　5　
当堂检测
3．如图，从电线杆离地面8 m处向地面拉一条钢索，如果这条钢索在地面的固定点距离电线杆底部 6 m，那么需要钢索的长度是　 　m．
　10　
当堂检测
4．如图，所有的三角形都是直角三角形，四边形都是正方形，正方形 A，B，C，D的边长分别是3，4，1，2，则最大正方形E的面积为　 　．
　30　
当堂检测
5.如图，BC长为 3 cm，AB长为 4 cm，AF长为 12 cm．求正方形CDEF的面积．
解：在Rt△ABC中，∠B＝90°，
∴AC2＝AB2＋BC2＝42＋32＝25，∴AC＝5 cm．
在Rt△FAC中，∠FAC＝90°，
∴FC2＝FA2＋AC2＝122＋52＝169．
∴S正方形CDEF＝FC2＝169 cm2．
当堂检测
因为AC＝BC＝5 cm，AB＝6 cm，所以AD＝3 cm．
所以CD2＝AC2－AD2＝52－32＝16．
所以CD＝4 cm．
所以S△ABC＝AB·CD＝×6×4＝12(cm2)．
因此等腰三角形ABC的面积是12 cm2．
6.如图，求等腰三角形ABC的面积．
解：如图，过点C作CD⊥AB于点D．
答案图
当堂检测
7.如图，一座建筑物发生了火灾，消防车到达现场后，发现最多只能靠近建筑物底端5米，消防车的云梯最大升长为13米，求云梯可以达到该建筑物的最大高度．
解：如图，AB＝13米，BC＝5米，∠ACB＝90°，
在Rt△ABC中，由勾股定理可得AB2＝AC2＋BC2，
即 132＝AC2＋52，所以AC＝12米．
答：云梯可以达到该建筑物的最大高度为12米．
答案图
勾股定理的探索
如果直角三角形两直角边长分别为a，b，斜边长为 c ，那么a2+b2=c2
利用勾股定理进行计算
感谢收看