北师大八上1.1.2探索勾股定理

(共24张PPT)
第一章 勾股定理
1.1.2探索勾股定理
北师大版 数学 八年级 上册
学习目标
1.掌握用面积法如何验证勾股定理，并能应用勾股定理解决一些实际问题。
2.经历勾股定理的验证过程，体会数形结合的思想和从特殊到一般的思想。
情景导入
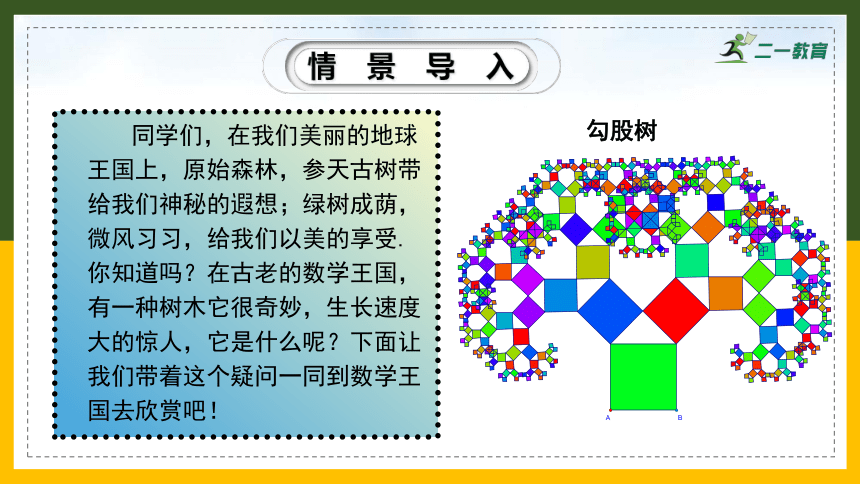
同学们，在我们美丽的地球王国上，原始森林，参天古树带给我们神秘的遐想；绿树成荫，微风习习，给我们以美的享受.你知道吗？在古老的数学王国，有一种树木它很奇妙，生长速度大的惊人，它是什么呢？下面让我们带着这个疑问一同到数学王国去欣赏吧！
勾股树
探索新知
勾股定理的验证
一
上节课我们认识了勾股定理，你还记得它的内容吗？那么如何验证勾股定理呢 ？
如果直角三角形的两条直角边长分别为a，b，斜边长为c，那么a2+b2=c2.
探索新知
证法一：赵爽弦图
b
b
a
a
c
c
a
b
边长分别为a，b的两个正方形分割成四个直角三角形和一个小正方形.
四个直角三角形和一个小正方形拼接成边长为c的大正方形.
探索新知
b
b
a
a
c
a
c
b
如图，左边图形的面积= a2+b2，右边图形的面积=c2.
∵右边图形由左边图形拼接而成，
∴得到a2+b2=c2 .
探索新知
证法二：加菲尔德总统拼图
b
b
a
a
c
c
┐
┌
┌
（1）
+
（2）
∴ a2+b2=c2.
探索新知
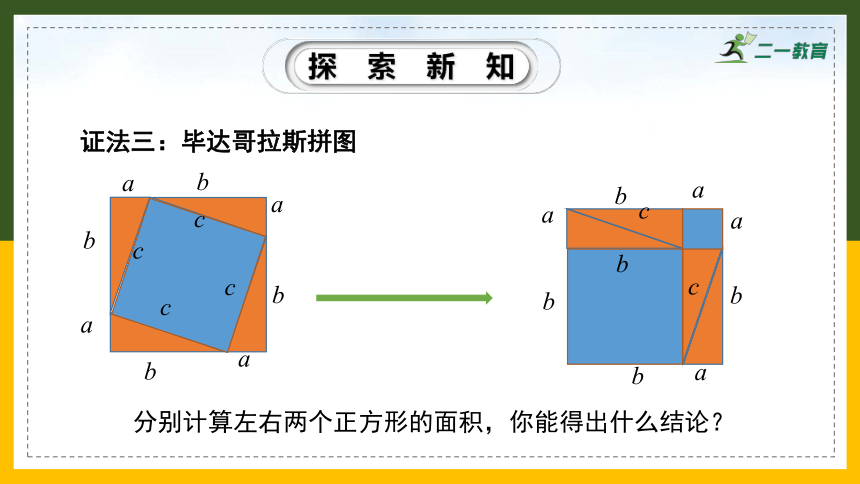
证法三：毕达哥拉斯拼图
b
b
b
b
a
a
a
a
c
c
c
c
b
b
b
b
a
a
b
a
a
c
c
分别计算左右两个正方形的面积，你能得出什么结论？
探索新知
b
b
b
b
a
a
a
a
c
c
c
c
b
b
b
b
a
a
b
a
a
c
c
4
4
探索新知
证法四：刘徽“青朱出入图”
设大正方形的面积为S，则S=
根据“出入相补，以盈补虚”的原理，得S=.
∴ =.
a
b
c
青出
青出
青入
青入
朱入
朱出
青方
朱方
总结归纳
探索新知
勾股定理的验证主要是通过拼图法利用面积的关系完成的，拼图又常以补拼法和叠合法两种方式拼图，补拼是要求无重叠，叠合是要求无空隙；而用面积法验证的关键是要找到一些特殊图形(如直角三角形、正方形、梯形)的面积之和等于整个图形的面积，从而达到验证的目的．
探索新知
勾股定理的简单应用
二
例1：飞机在空中水平飞行，某一时刻刚好飞到一个男孩子头顶上方4km处，过了20s，飞机距离这个男孩子头顶5km，飞机每小时飞行多少千米？
4km
20秒后
5km
A
B
C
探索新知
在Rt△ABC中，BC2=AB2-AC2.
解：
因为AB=5，AC=4,
所以BC2=52-42.
所以BC2=9,所以BC=3，
因为20s=h,
所以3÷=540km.
答：飞机每小时飞行540km.
4km
20秒后
5km
A
B
C
探索新知
例2： 等腰三角形底边上的高为8cm，周长为32cm，求这个三角形的面积.
8
x
16-x
D
A
B
C
解：设这个三角形为ABC，高为AD，设BD为xcm，则AB为（16-x）cm，
由勾股定理得：x2+82=(16-x)2
即x2+64=256-32x+x2
所以x=6
答：这个三角形的面积为48cm2.
S△ABC=BC AD=×2×6×8=48（cm2）
例3.如图,太阳能热水器的支架AB长为90 cm,与AB垂直的BC长为120 cm.太阳能真空管AC有多长
解：在Rt△ABC中,由勾股定理,
得 AC2=AB2+BC2，
AC2=902+1202，
AC=150(cm).
答:太阳能真空管AC长150 cm.
探索新知
当堂检测
1.我国是最早了解勾股定理的国家之一．下面四幅图中，不能验证勾股定理的是( )
C
当堂检测
2．如图①是边长分别为a，b的两个正方形，经如图②所示的割补可以得到边长为c的正方形，且面积等于割补前的两正方形面积之和．现请你通过对图②的观察指出下面对割补过程的理解不正确的是( )
A．割⑤补⑥
B．割③补①
C．割①补④
D．割③补②
B
当堂检测
3.如图，强大的台风使得一根旗杆在离地面3 m处折断倒下，旗杆顶部落在离旗杆底部4 m处，则旗杆折断之前高　 　m．
　 8　
当堂检测
4.如图，王大爷准备建一个蔬菜大棚，棚宽8m，高6m，长20m，棚的斜面用塑料薄膜遮盖，不计墙的厚度，阳光透过的最大面积是_________.
200m2
当堂检测
5.如图，长方形ABCD沿直线AE折叠，顶点D正好落在BC边上的F点处，已知CE＝3，AB＝8，求图中阴影部分的面积．
解：由折叠的性质，知EF＝DE＝CD－CE＝5，
AD＝AF＝BC，
由勾股定理，得CF＝4，AF2＝AB2＋BF2，
即AD2＝82＋(AD－4)2，
解得AD＝10，∴BF＝6，
∴图中阴影部分的面积＝S△ABF＋S△CEF＝30．
当堂检测
6.如图，甲轮船以16海里/时的速度离开港口O向东南方向航行，乙轮船同时同地向西南方向航行，已知它们离开港口一个半小时后分别到达A，B两点，且知AB＝30海里，则乙轮船每小时航行多少海里？
当堂检测
解：∵甲轮船向东南方向航行，乙轮船向西南方向航行，∴AO⊥BO，
∵甲轮船以每小时16海里的速度航行了一个半小时，
∴OA＝16×1.5＝24海里，又AB＝30海里，
在Rt△AOB中，由勾股定理，可得OA2＋OB2＝AB2，
即242＋OB2＝302，∴OB＝18海里，
∴乙轮船每小时航行18÷1.5＝12海里．
答：乙轮船每小时航行12海里．
勾股定理
证明
应用
刘徽“青朱出入图”
加菲尔德总统拼图
毕达哥拉斯拼图
赵爽弦图
感谢收看