第二十二章 二次函数 跟踪练习(含答案) 2024--2025学年人教版九年级数学上册
文档属性
| 名称 | 第二十二章 二次函数 跟踪练习(含答案) 2024--2025学年人教版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 443.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 18:39:06 | ||
图片预览



文档简介
第二十二章 二次函数 跟踪练习 2024--2025学年人教版九年级数学上册
一、单选题
1.若,,为二次函数图象上的三点,则,,的大小关系是( )
A. B. C. D.
2.点P1(-1,y1),P2(3,y2),P3(5,y3)均在函数y=-x2+2x+c的图象上,则( )
A.y1=y2>y3 B.y1>y2>y3 C.y3>y2>y1 D.y3>y1=y2
3.把抛物线 向右平移1个单位,所得抛物线的函数表达式为
A. B. C. D.
4.二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=﹣1,与x轴的交点为(x1,0)、(x2,0),其中0<x1<1,有下列结论:①abc>0;②﹣3<x2<﹣2;③4a﹣2b+c<﹣1;④当m为任意实数时,a﹣b<am2+bm;⑤若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑥a> .其中,正确结论的个数为( )
A.2 B.3 C.4 D.5
5.若二次函数 的图像与 轴有两个交点,则实数 的取值范围是( )
A. B. C. D.
6.抛物线(为常数,)经过点,对称轴为直线,顶点在第三象限.有下列结论:①;②;③当时(为常数),.其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
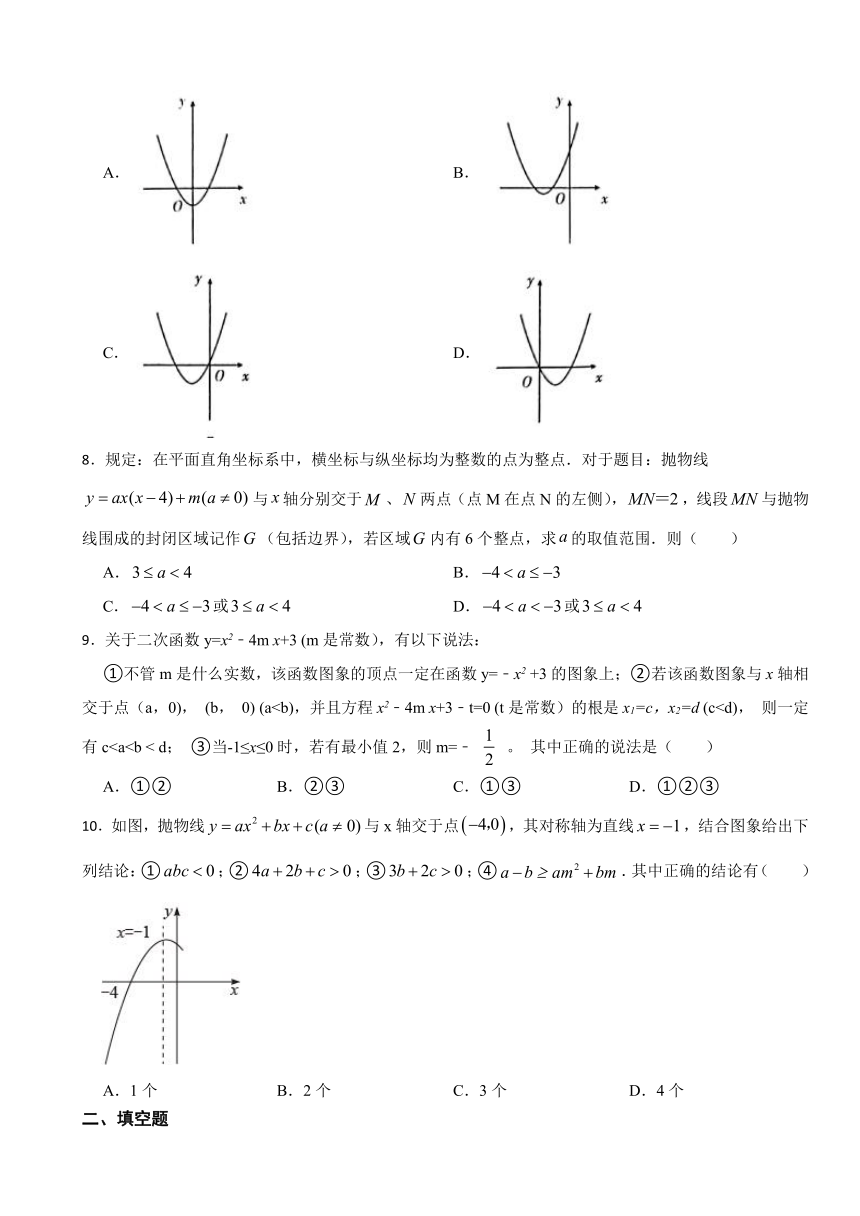
7.若 是二次函数 图象上一点,则抛物线 的图象可能是( )
A. B.
C. D.
8.规定:在平面直角坐标系中,横坐标与纵坐标均为整数的点为整点.对于题目:抛物线与轴分别交于、两点(点M在点N的左侧),,线段与抛物线围成的封闭区域记作(包括边界),若区域内有6个整点,求的取值范围.则( )
A. B.
C.或 D.或
9.关于二次函数y=x2﹣4m x+3 (m是常数),有以下说法:
①不管m是什么实数,该函数图象的顶点一定在函数y=﹣x2 +3的图象上;②若该函数图象与x轴相交于点(a,0), (b, 0) (aA.①② B.②③ C.①③ D.①②③
10.如图,抛物线与x轴交于点,其对称轴为直线,结合图象给出下列结论:①;②;③;④.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
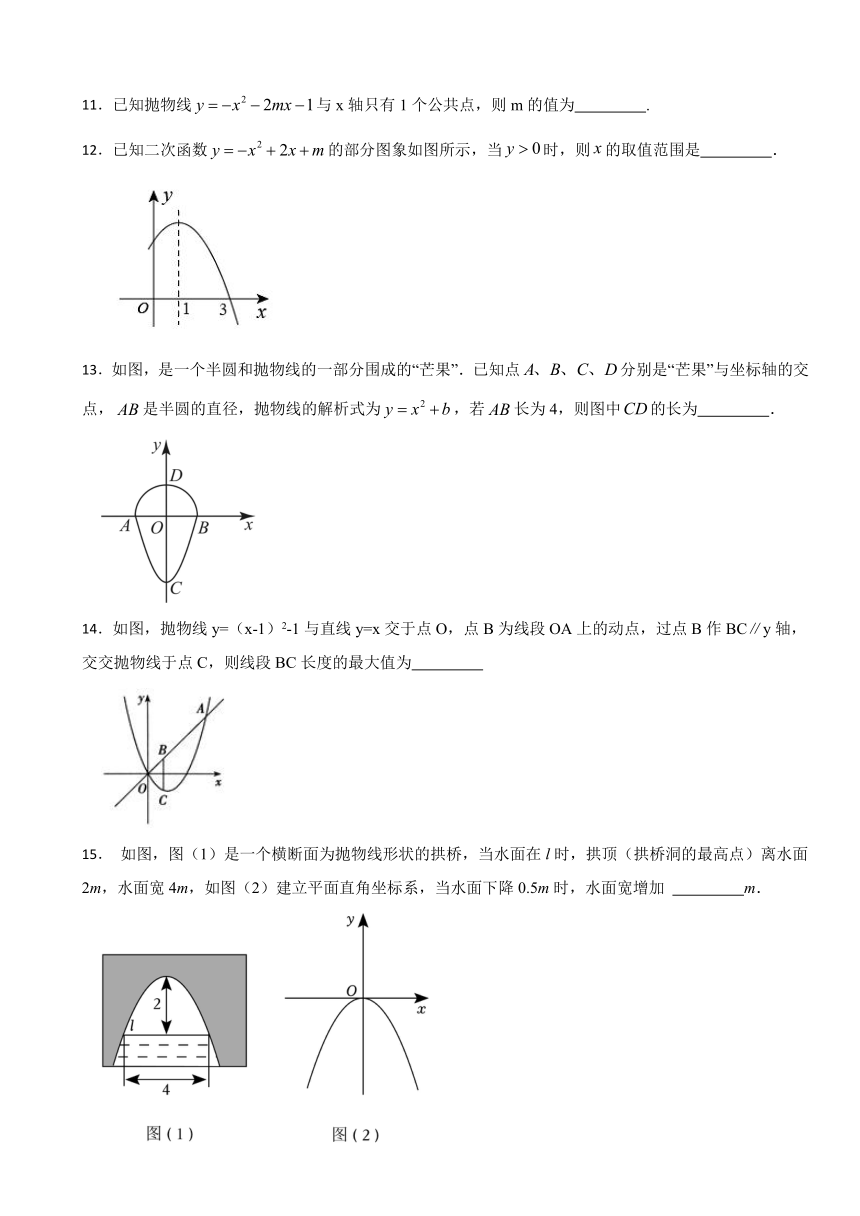
11.已知抛物线与x轴只有1个公共点,则m的值为 .
12.已知二次函数的部分图象如图所示,当时,则的取值范围是 .
13.如图,是一个半圆和抛物线的一部分围成的“芒果”.已知点分别是“芒果”与坐标轴的交点,是半圆的直径,抛物线的解析式为,若长为4,则图中的长为 .
14.如图,抛物线y=(x-1)2-1与直线y=x交于点O,点B为线段OA上的动点,过点B作BC∥y轴,交交抛物线于点C,则线段BC长度的最大值为
15. 如图,图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m,如图(2)建立平面直角坐标系,当水面下降0.5m时,水面宽增加 m.
16.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=-1,下列结论:① b2>4ac;② abc>0;③ a-c<0;④ am2+bm≥a-b(m为任意实数),其中正确的结论是
17.已知二次函数图象如图所示,有下列4个结论:①;②;③;④;其中正确的结论 .
三、解答题
18.(1)已知二次函数图象的顶点坐标为,且经过点,求这个二次函数的表达式.
(2)已知二次函数的图象经过点、和,求这个二次函数的表达式.
19.已知抛物线:.
(1)请写出抛物线的对称轴:直线___________;
(2)时,将该抛物线沿x轴翻折,得到新的抛物线对应的函数表达式是___________;
(3)若抛物线的顶点在x轴上,求a的值.
20.2023年杭州亚运会胜利闭幕,本次亚运会中国代表团共获得383枚奖牌,位居奖牌榜第一位,创造了新的历史。在亚运会期间,买一件印有亚运会元素的T恤去看比赛,成为了体育迷们的“仪式感”。商店以40元每件的价格购进一批这样的T恤,以每件60元的价格出售。经统计,四月份的销售量为192件,六月份的销售量为300件。
(1)求该款T恤四月份到六月份销售量的月平均增长率。
(2)从七月份起,商场决定采用降价销售回馈顾客,经试验,发现该款T恤在六月销售量的基础上,每降1元,月销售量就会增加20件。如何定价才能使利润最大?
21. 某公园要修建一个圆形喷水池,在池中心竖直安装一根水管,水管长在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高,高度为.
(1)建立如图所示平面直角坐标系,求在第一象限部分的抛物线的解析式;
(2)不考虑其它因素,求水池的直径至少要多少米才能使喷出的水流不落到池外.
22. 在平面直角坐标系中,抛物线过点.
(1)求用含的式子表示;
(2)抛物线过点,,,
①证明:;
②若,,恰有两个点在轴上方,求的取值范围.
23.在平面直角坐标系xOy中,已知抛物线,点.
(1)当抛物线过点时,求抛物线的解析式;
(2)证明:无论为何值,抛物线必过定点,并求出点的坐标;
(3)在(1)的条件下,抛物线与轴交于点,点是抛物线上位于第一象限的点,连接AB,PD交于点M,PD与轴交于点.设,问是否存在这样的点P,使得S有最大值?若存在,请求出点P的坐标,并求出S的最大值.
答案解析部分
1.【答案】A
2.【答案】A
3.【答案】D
4.【答案】B
5.【答案】D
6.【答案】C
7.【答案】D
8.【答案】C
9.【答案】C
10.【答案】B
11.【答案】±1
12.【答案】
13.【答案】6
14.【答案】
15.【答案】
16.【答案】①②④
17.【答案】①④
18.【答案】(1);(2)
19.【答案】(1)
(2)
(3)
20.【答案】(1)解:设4月份到6月销售量的月平均增长率为a,
则,
解得:,(舍去),
答:4月份到6月份销售量的月平均增长率为;
(2)解:设定价为x元,利润为y元,
则,
对称轴为,
,
∴当时,y有最大值,
定价为元时利润最大.
21.【答案】(1)解:由题意可知,抛物线的顶点坐标为,
设抛物线的解析式为:,
将代入得,,
解得,
抛物线的解析式为:
(2)解:令,得,,
解得舍或,
米,
水池的直径至少要米才能使喷出的水流不落到池外.
22.【答案】(1)解:把代入,得
,
∴;
(2)解:①把代入,得
,
由(1)知:,
∴,
把代入,得
,
,
当时,,,
∴,
当时,,,
∴,
绽上,;
②由(1)知,
∴
∴抛物线对称轴为.
∵抛物线过点,,,
∴,,.
当时,抛物线开口向上,对称轴为,
∴抛物线在时,取得最小值.
∵,,恰有两点在轴上方,
∴,在轴上方,在轴上或轴下方.
∴,解得.
当时,抛物线开口向下,对称轴为,
∴抛物线在时,取得最大值,且.
∵,,恰有两点在轴上方,
∴,在轴上方,在轴上或轴下方.
∴,解得.
综上,的取值范围是或.
23.【答案】(1)解:把x=3,y=0代入y=-x2+2mx+3m得,
-9+6m+3m=0,
∴m=1,
∴y=-x2+2x+3;
(2)证明:∵y=-x2+m(2x+3),
∴当2x+3=0时,即时,,
∴无论m为何值,抛物线必过定点D,点D的坐标是;
(3)解:如图,
连接OP,
设点P(m,-m2+2m+3),
设PD的解析式为:y=kx+b,
∴,
∴,
∴PD的解析式为:y=,
当x=0时,y=,
∴点N的坐标是(0,),
∴,
∵S=S△PAM-S△BMN,
∴S=(S△PAM+S四边形AONM)-(S四边形AONM+S△BMN)=S四边形AONP-S△AOB,
∵
,
当x=0时,y=-x2+2x+3=3,
∴点B的坐标是(0,3),OB=3,
,
∴==,
∴当时,,
当时,,
∴点的坐标是(1,4).
一、单选题
1.若,,为二次函数图象上的三点,则,,的大小关系是( )
A. B. C. D.
2.点P1(-1,y1),P2(3,y2),P3(5,y3)均在函数y=-x2+2x+c的图象上,则( )
A.y1=y2>y3 B.y1>y2>y3 C.y3>y2>y1 D.y3>y1=y2
3.把抛物线 向右平移1个单位,所得抛物线的函数表达式为
A. B. C. D.
4.二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为直线x=﹣1,与x轴的交点为(x1,0)、(x2,0),其中0<x1<1,有下列结论:①abc>0;②﹣3<x2<﹣2;③4a﹣2b+c<﹣1;④当m为任意实数时,a﹣b<am2+bm;⑤若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑥a> .其中,正确结论的个数为( )
A.2 B.3 C.4 D.5
5.若二次函数 的图像与 轴有两个交点,则实数 的取值范围是( )
A. B. C. D.
6.抛物线(为常数,)经过点,对称轴为直线,顶点在第三象限.有下列结论:①;②;③当时(为常数),.其中,正确结论的个数是( )
A.0 B.1 C.2 D.3
7.若 是二次函数 图象上一点,则抛物线 的图象可能是( )
A. B.
C. D.
8.规定:在平面直角坐标系中,横坐标与纵坐标均为整数的点为整点.对于题目:抛物线与轴分别交于、两点(点M在点N的左侧),,线段与抛物线围成的封闭区域记作(包括边界),若区域内有6个整点,求的取值范围.则( )
A. B.
C.或 D.或
9.关于二次函数y=x2﹣4m x+3 (m是常数),有以下说法:
①不管m是什么实数,该函数图象的顶点一定在函数y=﹣x2 +3的图象上;②若该函数图象与x轴相交于点(a,0), (b, 0) (a
10.如图,抛物线与x轴交于点,其对称轴为直线,结合图象给出下列结论:①;②;③;④.其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.已知抛物线与x轴只有1个公共点,则m的值为 .
12.已知二次函数的部分图象如图所示,当时,则的取值范围是 .
13.如图,是一个半圆和抛物线的一部分围成的“芒果”.已知点分别是“芒果”与坐标轴的交点,是半圆的直径,抛物线的解析式为,若长为4,则图中的长为 .
14.如图,抛物线y=(x-1)2-1与直线y=x交于点O,点B为线段OA上的动点,过点B作BC∥y轴,交交抛物线于点C,则线段BC长度的最大值为
15. 如图,图(1)是一个横断面为抛物线形状的拱桥,当水面在l时,拱顶(拱桥洞的最高点)离水面2m,水面宽4m,如图(2)建立平面直角坐标系,当水面下降0.5m时,水面宽增加 m.
16.二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴为直线x=-1,下列结论:① b2>4ac;② abc>0;③ a-c<0;④ am2+bm≥a-b(m为任意实数),其中正确的结论是
17.已知二次函数图象如图所示,有下列4个结论:①;②;③;④;其中正确的结论 .
三、解答题
18.(1)已知二次函数图象的顶点坐标为,且经过点,求这个二次函数的表达式.
(2)已知二次函数的图象经过点、和,求这个二次函数的表达式.
19.已知抛物线:.
(1)请写出抛物线的对称轴:直线___________;
(2)时,将该抛物线沿x轴翻折,得到新的抛物线对应的函数表达式是___________;
(3)若抛物线的顶点在x轴上,求a的值.
20.2023年杭州亚运会胜利闭幕,本次亚运会中国代表团共获得383枚奖牌,位居奖牌榜第一位,创造了新的历史。在亚运会期间,买一件印有亚运会元素的T恤去看比赛,成为了体育迷们的“仪式感”。商店以40元每件的价格购进一批这样的T恤,以每件60元的价格出售。经统计,四月份的销售量为192件,六月份的销售量为300件。
(1)求该款T恤四月份到六月份销售量的月平均增长率。
(2)从七月份起,商场决定采用降价销售回馈顾客,经试验,发现该款T恤在六月销售量的基础上,每降1元,月销售量就会增加20件。如何定价才能使利润最大?
21. 某公园要修建一个圆形喷水池,在池中心竖直安装一根水管,水管长在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为处达到最高,高度为.
(1)建立如图所示平面直角坐标系,求在第一象限部分的抛物线的解析式;
(2)不考虑其它因素,求水池的直径至少要多少米才能使喷出的水流不落到池外.
22. 在平面直角坐标系中,抛物线过点.
(1)求用含的式子表示;
(2)抛物线过点,,,
①证明:;
②若,,恰有两个点在轴上方,求的取值范围.
23.在平面直角坐标系xOy中,已知抛物线,点.
(1)当抛物线过点时,求抛物线的解析式;
(2)证明:无论为何值,抛物线必过定点,并求出点的坐标;
(3)在(1)的条件下,抛物线与轴交于点,点是抛物线上位于第一象限的点,连接AB,PD交于点M,PD与轴交于点.设,问是否存在这样的点P,使得S有最大值?若存在,请求出点P的坐标,并求出S的最大值.
答案解析部分
1.【答案】A
2.【答案】A
3.【答案】D
4.【答案】B
5.【答案】D
6.【答案】C
7.【答案】D
8.【答案】C
9.【答案】C
10.【答案】B
11.【答案】±1
12.【答案】
13.【答案】6
14.【答案】
15.【答案】
16.【答案】①②④
17.【答案】①④
18.【答案】(1);(2)
19.【答案】(1)
(2)
(3)
20.【答案】(1)解:设4月份到6月销售量的月平均增长率为a,
则,
解得:,(舍去),
答:4月份到6月份销售量的月平均增长率为;
(2)解:设定价为x元,利润为y元,
则,
对称轴为,
,
∴当时,y有最大值,
定价为元时利润最大.
21.【答案】(1)解:由题意可知,抛物线的顶点坐标为,
设抛物线的解析式为:,
将代入得,,
解得,
抛物线的解析式为:
(2)解:令,得,,
解得舍或,
米,
水池的直径至少要米才能使喷出的水流不落到池外.
22.【答案】(1)解:把代入,得
,
∴;
(2)解:①把代入,得
,
由(1)知:,
∴,
把代入,得
,
,
当时,,,
∴,
当时,,,
∴,
绽上,;
②由(1)知,
∴
∴抛物线对称轴为.
∵抛物线过点,,,
∴,,.
当时,抛物线开口向上,对称轴为,
∴抛物线在时,取得最小值.
∵,,恰有两点在轴上方,
∴,在轴上方,在轴上或轴下方.
∴,解得.
当时,抛物线开口向下,对称轴为,
∴抛物线在时,取得最大值,且.
∵,,恰有两点在轴上方,
∴,在轴上方,在轴上或轴下方.
∴,解得.
综上,的取值范围是或.
23.【答案】(1)解:把x=3,y=0代入y=-x2+2mx+3m得,
-9+6m+3m=0,
∴m=1,
∴y=-x2+2x+3;
(2)证明:∵y=-x2+m(2x+3),
∴当2x+3=0时,即时,,
∴无论m为何值,抛物线必过定点D,点D的坐标是;
(3)解:如图,
连接OP,
设点P(m,-m2+2m+3),
设PD的解析式为:y=kx+b,
∴,
∴,
∴PD的解析式为:y=,
当x=0时,y=,
∴点N的坐标是(0,),
∴,
∵S=S△PAM-S△BMN,
∴S=(S△PAM+S四边形AONM)-(S四边形AONM+S△BMN)=S四边形AONP-S△AOB,
∵
,
当x=0时,y=-x2+2x+3=3,
∴点B的坐标是(0,3),OB=3,
,
∴==,
∴当时,,
当时,,
∴点的坐标是(1,4).
同课章节目录
