北师大版数学八年级上册 专项训练(二) 位置与坐标、一次函数(无答案)
文档属性
| 名称 | 北师大版数学八年级上册 专项训练(二) 位置与坐标、一次函数(无答案) | 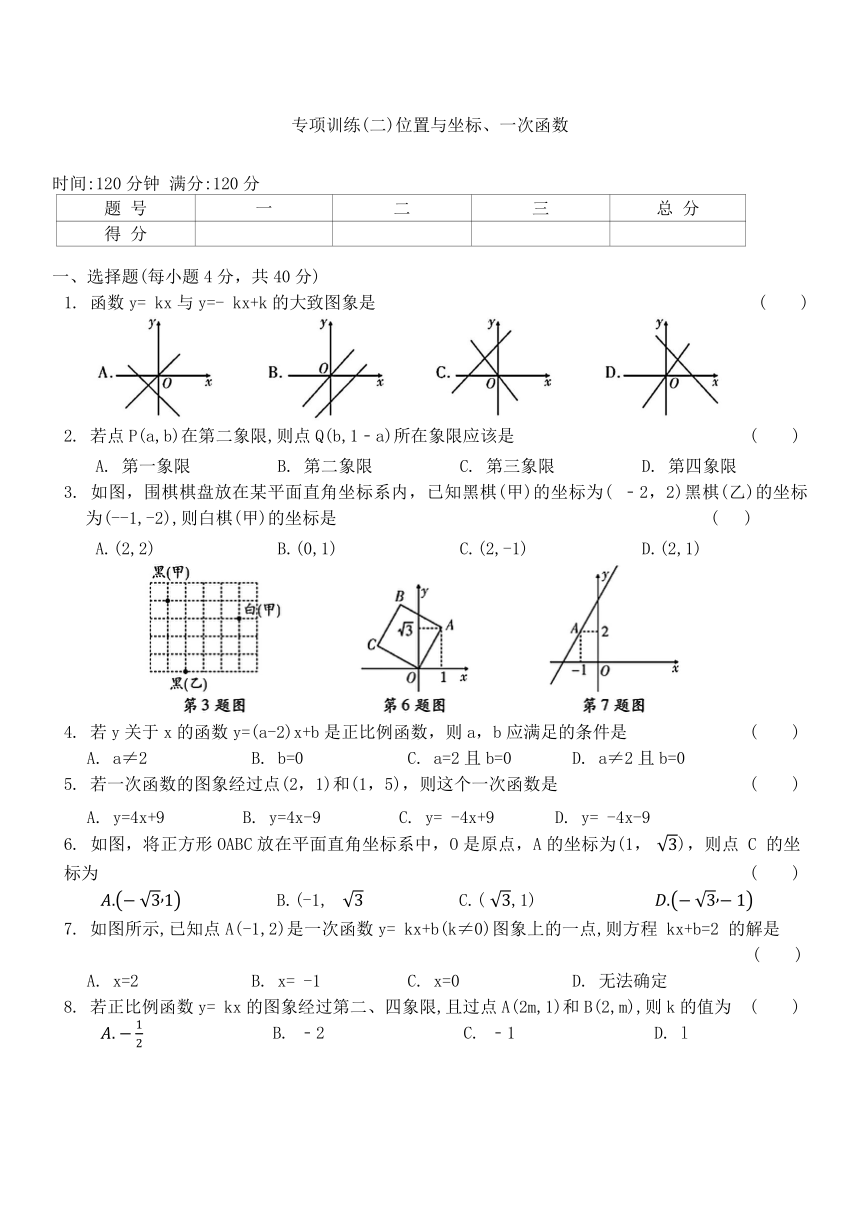 | |
| 格式 | docx | ||
| 文件大小 | 507.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-10-22 18:55:48 | ||
图片预览


文档简介
专项训练(二)位置与坐标、一次函数
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
1. 函数y= kx与y=- kx+k的大致图象是 ( )
2. 若点P(a,b)在第二象限,则点Q(b,1﹣a)所在象限应该是 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 如图,围棋棋盘放在某平面直角坐标系内,已知黑棋(甲)的坐标为( ﹣2,2)黑棋(乙)的坐标为(--1,-2),则白棋(甲)的坐标是 ( )
A.(2,2) B.(0,1) C.(2,-1) D.(2,1)
4. 若y关于x的函数y=(a-2)x+b是正比例函数,则a,b应满足的条件是 ( )
A. a≠2 B. b=0 C. a=2且b=0 D. a≠2且b=0
5. 若一次函数的图象经过点(2,1)和(1,5),则这个一次函数是 ( )
A. y=4x+9 B. y=4x-9 C. y= -4x+9 D. y= -4x-9
6. 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, ),则点 C 的坐标为 ( )
B.(-1, C.( ,1)
7. 如图所示,已知点A(-1,2)是一次函数y= kx+b(k≠0)图象上的一点,则方程 kx+b=2 的解是 ( )
A. x=2 B. x= -1 C. x=0 D. 无法确定
8. 若正比例函数y= kx的图象经过第二、四象限,且过点A(2m,1)和B(2,m),则k的值为 ( )
B. ﹣2 C. ﹣1 D. l
9. 小涵与阿嘉一起去咖啡店购买同款咖啡豆,咖啡豆每公克的价钱固定,购买时自备容器则结帐金额再减5元.若小涵购买咖啡豆250公克且自备容器,需支付295元;阿嘉购买咖啡豆x公克但没有自备容器,需支付y元,则y与x的关系式是 ( )
10. 一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为x(h),两车之间的距离为y( km),如图中的折线表示γ与x之间的函数关系,下列说法:
①动车的速度是270 km/h;
②点 B的实际意义是两车出发后3 h相遇;
③甲、乙两地相距1000 km;
④普通列车从乙地到达甲地时间是9 h.
其中不正确的有 ( )
A. 1 个 B. 2个 C. 3 个 D. 4个
二、填空题(每小题4分,共24分)
11. 已知点P(x-3,2x-4)在纵轴上,则x的值是 .
12. 若y是关于x的一次函数,当x的值减小1,y的值就减小2,则当x的值增加2时,y的值增加
13. 在平面直角坐标系中,点P(4,2)关于直线x=1的对称点的坐标是 .
14. 已知点A(a,b)在直线y=-3x+5上,则6a+2b-1的值为 .
15. 坐标平面上横、纵坐标都为整数的点叫做整点,已知A为整点,O为坐标原点, 那么A 点不同的位置一共有 个.
16. 为方便市民出行,北京地铁推出了电子定期票,电子定期票在使用有效期限内,支持单人不限次数乘坐北京轨道交通全路网(不含机场线)所有线路,电子定期票包括一日票、二日票、三日票、五日票及七日票共五个种类,价格如下表:
种类 一日票 二日票 三日票 五日票 七日票
单价(元/张) 20 30 40 70 90
某人需要连续6天不限次数乘坐地铁,若决定购买电子定期票,则总费用最低为 元.
三、解答题(共56分)
17. (6分)点P到y轴的距离与它到点 A( -8,2)的距离都等于13,求点P的坐标.
18. (6分)已知一次函数
(1)当a、b为何值时,y随x的增大而增大
(2)当a、b为何值时,图象与y轴交点在x轴上方
(3)当a、b为何值时,图象过原点
19. (7分)在平面直角坐标系中,有点.
(1)若线段 轴,求点A,B的坐标.
(2)当点B到y轴的距离与点A到x轴的距离相等时,求点 B所在的象限.
20. (8分)小慧家与文具店相距960m,小慧从家出发,沿笔直的公路匀速步行12 min来到文具店买笔记本,停留3 min,因家中有事,便沿着原路匀速跑步6m in返回家中.
(1)小慧返回家中的速度比去文具店的速度快多少
(2)请你画出这个过程中,小慧离家的距离y与时间x的函数图象.
(3)根据图象回答,小慧从家出发后多少分钟离家距离为720 m
21. (8分)已知点A(1,1),B(-1,1),C(0,4).
(1)在平面直角坐标系中描出A,B,C三点.
(2)在同一平面内,点与三角形的位置关系有三种:点在三角形内、点在三角形边上、点在三角形外.若点 P 在 外,请判断点P关于y轴的对称点. 与 的位置关系,直接写出判断结果.
22. (9分)如图1,直线 k,b为常数)交x轴的正半轴于点A(4,0),交y轴正半轴于点B,
(1)求直线AB的表达式.
(2)点C是线段AB中点,点P是x轴负半轴上一点,连接PC,设点P 的横坐标为t, 的面积为m,求m与t之间的函数关系式(不要求写出自变量的取值范围).
23. (11 分)在抗击新冠肺炎这场没有硝烟的战疫中,无人机成为全国各地广大农村乃至城区防疫消杀工作的“超级神器”,通过无人机隔空喊话宣传劝导,这使无人机成为宣传小能手.某市区也启用无人机进行防疫巡视及宣传工作,在操控无人机时,需根据现场状况调节无人机飞行高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行时间为x( min),对应的飞行高度为y(m),且y与x之间的函数图象如图所示.
(1)求线段BC所表示的y与x之间的函数关系式.
(2)求无人机在50m上空持续飞行的时间.
时间:120分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(每小题4分,共40分)
1. 函数y= kx与y=- kx+k的大致图象是 ( )
2. 若点P(a,b)在第二象限,则点Q(b,1﹣a)所在象限应该是 ( )
A. 第一象限 B. 第二象限 C. 第三象限 D. 第四象限
3. 如图,围棋棋盘放在某平面直角坐标系内,已知黑棋(甲)的坐标为( ﹣2,2)黑棋(乙)的坐标为(--1,-2),则白棋(甲)的坐标是 ( )
A.(2,2) B.(0,1) C.(2,-1) D.(2,1)
4. 若y关于x的函数y=(a-2)x+b是正比例函数,则a,b应满足的条件是 ( )
A. a≠2 B. b=0 C. a=2且b=0 D. a≠2且b=0
5. 若一次函数的图象经过点(2,1)和(1,5),则这个一次函数是 ( )
A. y=4x+9 B. y=4x-9 C. y= -4x+9 D. y= -4x-9
6. 如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, ),则点 C 的坐标为 ( )
B.(-1, C.( ,1)
7. 如图所示,已知点A(-1,2)是一次函数y= kx+b(k≠0)图象上的一点,则方程 kx+b=2 的解是 ( )
A. x=2 B. x= -1 C. x=0 D. 无法确定
8. 若正比例函数y= kx的图象经过第二、四象限,且过点A(2m,1)和B(2,m),则k的值为 ( )
B. ﹣2 C. ﹣1 D. l
9. 小涵与阿嘉一起去咖啡店购买同款咖啡豆,咖啡豆每公克的价钱固定,购买时自备容器则结帐金额再减5元.若小涵购买咖啡豆250公克且自备容器,需支付295元;阿嘉购买咖啡豆x公克但没有自备容器,需支付y元,则y与x的关系式是 ( )
10. 一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车均匀速行驶并同时出发,设普通列车行驶的时间为x(h),两车之间的距离为y( km),如图中的折线表示γ与x之间的函数关系,下列说法:
①动车的速度是270 km/h;
②点 B的实际意义是两车出发后3 h相遇;
③甲、乙两地相距1000 km;
④普通列车从乙地到达甲地时间是9 h.
其中不正确的有 ( )
A. 1 个 B. 2个 C. 3 个 D. 4个
二、填空题(每小题4分,共24分)
11. 已知点P(x-3,2x-4)在纵轴上,则x的值是 .
12. 若y是关于x的一次函数,当x的值减小1,y的值就减小2,则当x的值增加2时,y的值增加
13. 在平面直角坐标系中,点P(4,2)关于直线x=1的对称点的坐标是 .
14. 已知点A(a,b)在直线y=-3x+5上,则6a+2b-1的值为 .
15. 坐标平面上横、纵坐标都为整数的点叫做整点,已知A为整点,O为坐标原点, 那么A 点不同的位置一共有 个.
16. 为方便市民出行,北京地铁推出了电子定期票,电子定期票在使用有效期限内,支持单人不限次数乘坐北京轨道交通全路网(不含机场线)所有线路,电子定期票包括一日票、二日票、三日票、五日票及七日票共五个种类,价格如下表:
种类 一日票 二日票 三日票 五日票 七日票
单价(元/张) 20 30 40 70 90
某人需要连续6天不限次数乘坐地铁,若决定购买电子定期票,则总费用最低为 元.
三、解答题(共56分)
17. (6分)点P到y轴的距离与它到点 A( -8,2)的距离都等于13,求点P的坐标.
18. (6分)已知一次函数
(1)当a、b为何值时,y随x的增大而增大
(2)当a、b为何值时,图象与y轴交点在x轴上方
(3)当a、b为何值时,图象过原点
19. (7分)在平面直角坐标系中,有点.
(1)若线段 轴,求点A,B的坐标.
(2)当点B到y轴的距离与点A到x轴的距离相等时,求点 B所在的象限.
20. (8分)小慧家与文具店相距960m,小慧从家出发,沿笔直的公路匀速步行12 min来到文具店买笔记本,停留3 min,因家中有事,便沿着原路匀速跑步6m in返回家中.
(1)小慧返回家中的速度比去文具店的速度快多少
(2)请你画出这个过程中,小慧离家的距离y与时间x的函数图象.
(3)根据图象回答,小慧从家出发后多少分钟离家距离为720 m
21. (8分)已知点A(1,1),B(-1,1),C(0,4).
(1)在平面直角坐标系中描出A,B,C三点.
(2)在同一平面内,点与三角形的位置关系有三种:点在三角形内、点在三角形边上、点在三角形外.若点 P 在 外,请判断点P关于y轴的对称点. 与 的位置关系,直接写出判断结果.
22. (9分)如图1,直线 k,b为常数)交x轴的正半轴于点A(4,0),交y轴正半轴于点B,
(1)求直线AB的表达式.
(2)点C是线段AB中点,点P是x轴负半轴上一点,连接PC,设点P 的横坐标为t, 的面积为m,求m与t之间的函数关系式(不要求写出自变量的取值范围).
23. (11 分)在抗击新冠肺炎这场没有硝烟的战疫中,无人机成为全国各地广大农村乃至城区防疫消杀工作的“超级神器”,通过无人机隔空喊话宣传劝导,这使无人机成为宣传小能手.某市区也启用无人机进行防疫巡视及宣传工作,在操控无人机时,需根据现场状况调节无人机飞行高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行时间为x( min),对应的飞行高度为y(m),且y与x之间的函数图象如图所示.
(1)求线段BC所表示的y与x之间的函数关系式.
(2)求无人机在50m上空持续飞行的时间.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
